小型食品粉碎機的雙層隔振系統優化設計

朱秀琳 李成清 翁秀奇

（南京工業職業技術學院，江蘇 南京 210023）

小型食品粉碎機目前在中國使用非常普遍，給人們生活帶來諸多便利。盡管生產企業一直致力于產品功能完善，但是其振動與噪聲問題一直得到有根本解決。目前未發現有針對此類產品噪聲問題的研究見諸于文獻。

本設計以某款小型食品粉碎機（圖1）為研究對象，該機最高工作轉速為30 000r/min，正常工作時噪聲達到66dB，超過GB 3096—2008《聲環境質量標準》規定的“居民住宅小區區域環境噪聲平均等效聲級須達到環境質量1類標準，即晝間55dB，夜間45dB”。

該機由杯體1（盛食物、刀具由刀桿與機身內連接）、機身3（內裝有電機、軸承、電腦板等）組成。粉碎作業時，在電機高速旋轉下，電機、軸承、刀片、機身、杯體及被粉碎食品會出現振動，并產生噪聲。杯體與機身合縫處以及機身底部均有4只沿圓周均布的橡膠隔振墊，共同組成雙層隔振系統。本設計擬基于MATLAB編程與圖形功能，對隔振系統進行優化。

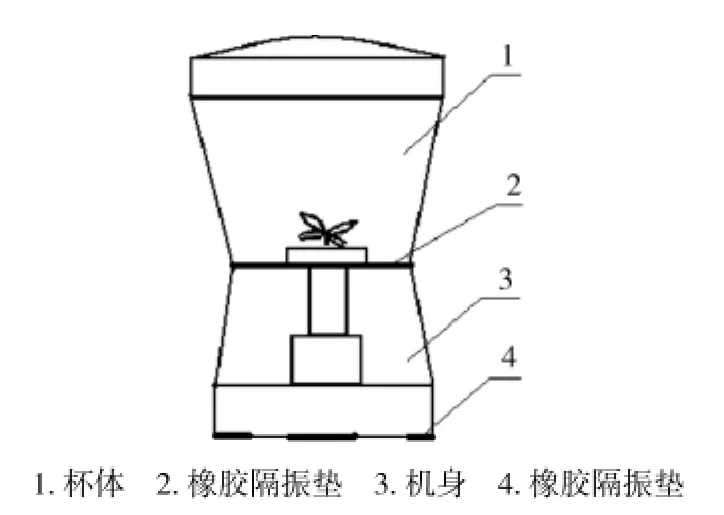
圖1 小型食品粉碎機Figure 1 A smal pulverizer

1 數學模型的建立

相對來說，杯體、機身比隔振墊的剛度大很多，故將杯體、機身簡化作剛體，質量分別為m1、m2，因塑料把手中空質量較輕忽略，故m1、m2的質心均在其圓柱中心線上。第1層3只隔振墊x向總剛度為K1、粘性阻尼系數為C1，第2層4只隔振墊x向總剛度為K2，粘性阻尼系數為C2。激勵力F（t）可以看做簡諧力，F（t）＝F0sinωt，傳入基礎的力為FT（t），x1、x2為絕對位移，其數學模型見圖2。

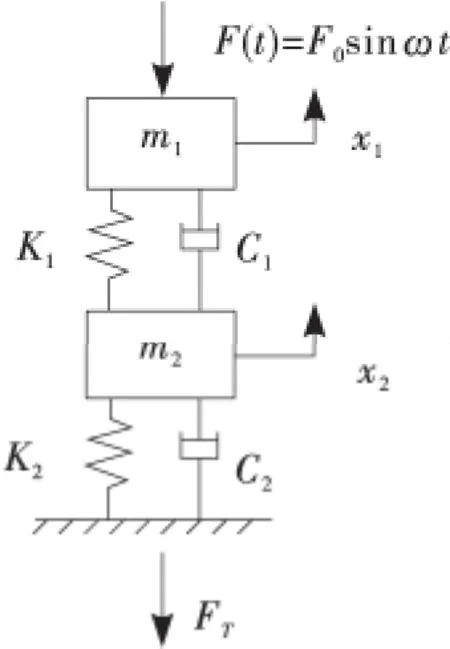
圖2 數學模型Figure 2 Mathematical model

根據牛頓第二定律，系統運動微分方程為［1］：

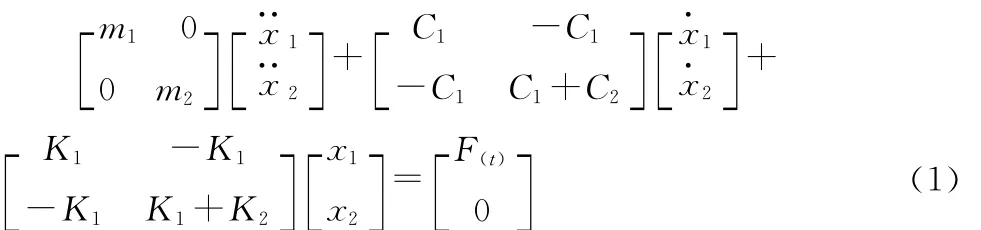
令FT（t）＝H（ω）F（t），解微分方程（1）可以得到系統頻響函數［1］：

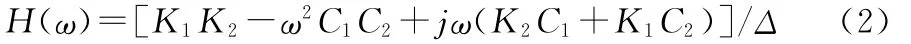
其中，Δ＝（K1－m1ω2＋jC1ω）［K1＋K2－m2ω2＋jω（C1＋C2）］－（K1＋jC1ω）2。

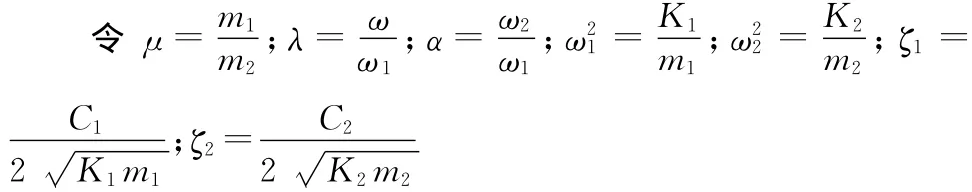
由式（2）整理得到用無因次量表示的頻響函數：

其中，A＝λ4－λ2（α2＋4ζ1ζ2α＋μ＋1）＋α2；C＝α2－4ζ1ζ2αλ2；B＝2λ3（ζ2α＋ζ1μ＋ζ1）－2λα（ζ1α＋ζ2）；D＝2λα（ζ1α＋ζ2）。

因此，雙層隔振系統的絕對傳遞率：

2 動態特性分析

單層隔振系統只要合理選擇剛度比、阻尼比參數，在低頻區（＜50Hz）能起到很好的隔振效果。但是對高頻干擾（＞100Hz）的隔振效果并不理想，并且隔振的頻段也比較窄［1－6］，而大部分結構噪聲都是高頻的。因此，雙層隔振應運而生，越過共振區后雙層隔振的傳遞率斜率從單層的12dB/oct增加到24dB/oct［1－6］，這對于高頻振動的隔離意義重大。

影響雙層隔振系統隔振性能的參數主要有質量比、阻尼比、固有頻率比。以頻率比λ為橫坐標、以隔振系統絕對傳遞率TA為縱坐標，分別以質量比、阻尼比、固有頻率比為參變量，基于MATLAB編程與圖形功能，由式（4）研究參變量變化時絕對傳遞率TA的變化規律。為了使圖形表達清晰，橫坐標取對數lgλ，縱坐標取振動級差變化的分貝數，即20lg｜H（λ）｜。

由圖3可知，隨著質量比μ的增大，振動傳遞率曲線的第1峰位置左移而第2峰位置右移，故隔振頻帶變寬，隔振效果變好，尤其在第1峰與第2峰之間效果最好。例如當ζ1＝0.03，ζ2＝0.05，α＝1.2，λ＝1，μ從1增加到4時，振動級差減小了12dB。但是在高頻區即第2峰后，質量比的變化對隔振效果影響不大。

由圖4可知，固有頻率比α的變化對隔振效果影響非常顯著，且分布在整個低頻及高頻區。隨著α的變大，隔振效果變差。例如當ζ1＝0.03，ζ20.05，μ＝1.538，α從1.4減少到0.5，λ＝1和λ＝10時，振動級差分別減小了17.96，18.75dB。

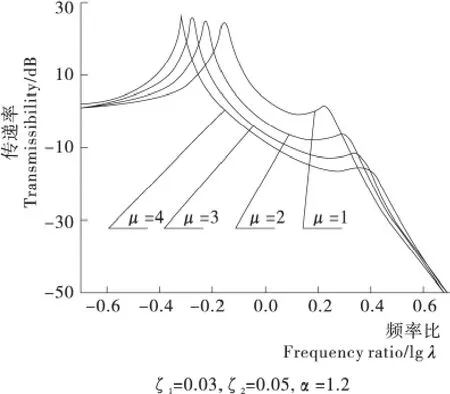
圖3 質量比變化對隔振效果的影響Figure 3 Magnification factors of vibrations at different mass ratio

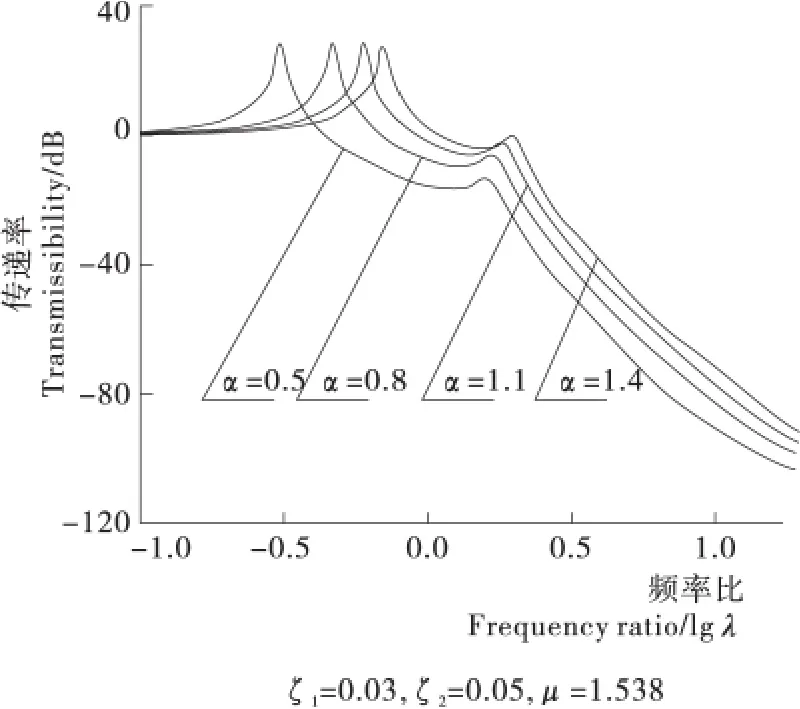
圖4 固有頻率比變化時對隔振效果的影響Figure 4 Magnification factors of vibrations at different natural frequency ratio

由圖5（a）可知，阻尼比ζ1變化時（取ζ1＝0.02～0.15，ζ2＝0.02，α＝1.5，μ＝1.538），在低頻區僅僅在共振區域隨著ζ1增大能明顯減小振動級差，而其他區域幾乎無影響。但是在高頻區（λ＞2.5）時，ζ1增大反而會降低隔振效果。例如當λ＝10，ζ1由0.02增加到0.15時，振動級差增加了9.7dB。

由圖5（b）可知，阻尼比ζ2變化時（取ζ2＝0.02～0.15，ζ1＝0.02，α＝1.5，μ＝1.538），在低頻區對隔振效果的影響與ζ1的相同，只是區域變寬（λ由2.5擴大到10）。在高頻區λ＞10，傳遞率曲線發生逆轉，即隨著ζ2的增大，反而會降低隔振效果。例如當λ＝33，ζ2由0.02增加到0.15時，振動級差增加了15.33dB。

3 優化設計

利用頻譜與相干分析法測試如圖1所示的小型食品粉碎機，其振動和噪聲頻率集中在368Hz，倍頻為744，1 104，1 472，2 216，2 584Hz，均屬于高頻振動范圍，因此，采用雙層隔振尤為必要。該機器也是如此設計的，但是噪聲指標仍然不達標。本設計擬利用MATLAB編程，采用單純形優化算法［7］，優化隔振系統從而達到減振降噪目的。

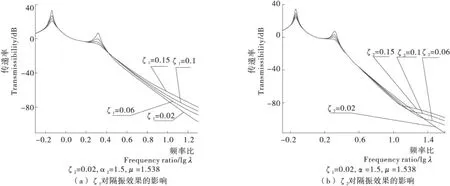
圖5 阻尼比變化對隔振效果的影響Figure 5 Magnification factors of vibrations at different damping ratio

3.1 目標函數

根據以上雙層隔振系統動態特性分析，在高頻區為增加隔振效果，應該盡量增加質量比μ、取較小的阻尼比ζ1和ζ2以及盡量減小固有頻率比α。但是，有些參數的改變是受限的。例如，增加質量比，如果增加機頭質量，則增加了整機重量，使小型家電變得笨重。如果減小機身重量，則要減少本來就很小巧的各種電子元器件質量。況且，在高頻區質量比的變化對隔振效果影響程度不大，所以，本機質量比（μ＝1.452）不做修改。

因此，本機雙層隔振系統參數優化主要從適當調整阻尼比、優化固有頻率比（選擇合適隔振墊固有頻率）的角度出發。

本設計以減小雙層隔振系統振動級差為目標。

3.2 約束條件

橡膠隔振墊的種類很多，其性能主要取決于橡膠配方、隔振墊形狀以及硫化工藝。目前中國標準化的橡膠隔振墊主要有XD型和WJ型［8，9］，也可根據隔振性能要求自行設計。橡膠的阻尼比較大，ζ可達0.15，但是常用范圍在0.02～0.08。橡膠墊的固有頻率范圍一般在10～20Hz［8，9］。即：

3.3 優化計算

采用無約束最優化直接算法：單純形法。此算法不用求導，雖然收斂較慢，但是編程簡單，由于本優化函數變量不多，也能收到較好效果。

經過測試，該機器各項動態特性原始參數為：機頭m1＝1.35kg（包含常規預估食物重量），機身m2＝0.93kg，ω1＝10Hz，ω2＝15Hz，ζ1＝0.10，ζ2＝0.07。輸入原始數據及約束條件，優化計算后結果見表1。可見，只要調整阻尼比ζ1、固有頻率ω2至表1中數值，本粉碎機的隔振系統在工作噪聲頻率區域的振動級差就會降低10～13dB。

3.4 系統改進

根據優化結果，重新選取新的隔振墊：即ζ1＝0.03，ω2＝10.5Hz，其它參數不變。按照相同步驟再次測試該機工作噪聲為53.9dB，已符合GB 3096—2008《聲環境質量標準》的規定。

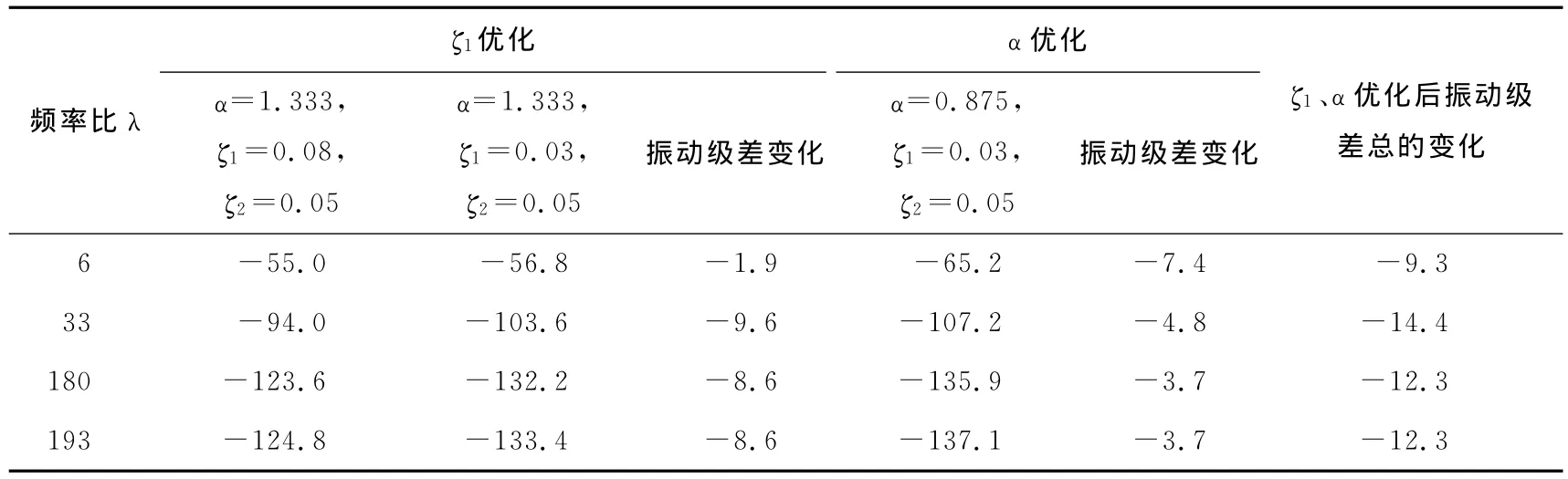
表1 粉碎機工作噪聲區域振動級差計算Table 1 Calculation of Magnification factors of vibrations on the noise area of the pulverizer dB

4 結論

基于MATLAB的編程、圖形與計算功能，分析了雙層隔振系統的各項動態參數對隔振性能的影響，在此基礎上利用單純形優化算法對該食品粉碎機的雙層隔振系統的參數進行了優化計算，然后根據優化結果重新選取隔振墊，經測試噪聲指標降低了12.1dB，解決了該機器工作噪聲超標的問題。

1 嚴濟寬.機械振動隔離技術［M］.上海：上海科學技術出版社，1985：21～93.

2 劉迎春，王開和.基于彈性體模型的雙層隔振器結構參數設計［J］.天津科技大學學報，2006，21（3）：57～19.

3 孫京平，王開和，盧學軍，等.水泵的雙層隔振設計［J］.機械設計與制造，2006（3）：5～7.

4 Cai Liang－bin，Chen Da－yue.A two－stage vibration isolation system featuring an electrorheological damper via the semiactive static output feedback variable structure control method［J］.Jounal of Vibration and Control，2004，10（5）：683～706.

5 蘇榮華，彭晨宇，丁文文.設計參數對雙層隔振系統動態性能影響的研究［J］.應用基礎與工程科學學報，2008，16（6）：863～869.

6 駱江峰.降低往復式壓縮機振動與噪聲的設計［J］.食品與機械，2006，22（6）：91～94.

7 陳寶林.最優化理論與算法［M］.北京：清華大學出版社，2005：341～369.

8 周新祥.噪聲控制技術及其新進展［M］.北京：冶金工業出版社，2007：152～160.

9 張弛.噪聲污染控制技術［M］.北京：中國環境科學出版社，2007：186～206.