兩均勻帶電長直導線的電場線方程的兩種推導方法
兩均勻帶電長直導線的電場線方程的兩種推導方法
姜付錦
(武漢市黃陂區第一中學湖北 武漢430300)
摘 要:本文采用解析函數的知識和徑向圓光柵的莫爾條紋理論分別從兩個不同的角度推導出了兩根無限長均勻帶電直導線的電場線方程,并用電腦軟件MathCAD對其電場線進行了數值模擬.
關鍵詞:解析函數莫爾條紋數值模擬
收稿日期:(2014-12-15)
文獻[1]描繪了兩根帶相等電量無限長直導線的電場線和等勢面的解析函數,但是沒有給出帶不等電量兩根無限長直導線的電場線方程.本文將用兩種方法來研究這個問題.
1建立模型
兩根相距為2a的無限長平行均勻帶電直導線,每根導線單位長度上所帶的電荷量分別為λ1,λ2,以垂直于兩根導線的連線為x軸,過連線中點O作垂線為y軸,建立平面直角坐標系xOy,如圖1所示.
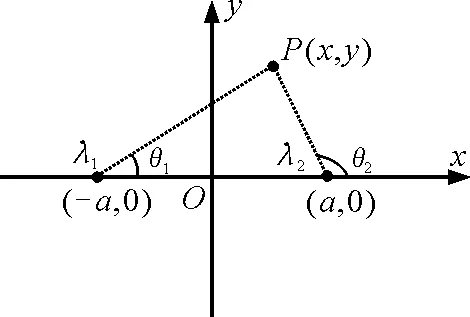
圖1 建立平面直角坐標系
由高斯定理[2]求得其中一根導線在空間產生的電場強度的大小為
式中r為空間某點到直導線的距離.
設xOy平面任意一點P的坐標為P(x,y),則兩根直導線在P點產生的合電場強度E的兩個分量為
Ex=E1cosθ1+E2cosθ2=
(1)
Ey=E1sinθ1+E2sinθ2=
(2)
2利用解析函數求解
設電勢為φ,電場強度為E,由于E=-φ,得任意一點P(x,y)的電場強度的兩個分量應滿足式(1)和式(2).

查表得[4]

上式中的E(x,y)為任意常量,則上式可化為

(3)
即兩根無限長帶電直導線的電場線的方程.式中C2為任意常數.
若將坐標系xOy的原點平移到(-a,0),則式(3)可化為
設λ1=kλ2(k為常數),由極坐標與平面直角坐標的關系式
x=ρcosφy=ρsinφ
(4)
將式(4)化為極坐標系的表達式
3利用徑向圓光柵的莫爾條紋推導[5,6]
作光柵平面xOy,規則排列的光柵線紋可以用整數n,m作為參變量,x,y作為函數表示出來.這樣兩光柵的柵線方程分別由f(x,y,n),g(x,y,m)的形式表示出來.由于兩柵線交點的軌跡是莫爾明條紋,因此莫爾條紋方程式就能由f(x,y,n),g(x,y,m)所給定.可以用f,g描述的柵線簇不僅僅限于直線,凡是規則排列的曲線簇都可以,更普遍的不只是平面曲線,即使是空間曲線也適用.這兩條光柵線分別代表的是兩根無限長均勻帶電直導線產生的電場線.
設兩光柵的角節距分別為γ1,γ2,偏心放置,偏心量OO1=2a,如圖2所示.取兩光柵中心連線OO1為x軸,與x軸垂直并通過主光柵中心O的為y軸,為使柵線方程簡單,使兩光柵各有一簇線紋與x軸正方向重合,并以此線為柵線編號n,m的起點,且令n,m為正或負整數(逆時針方向數為正,順時針方向數為負),則兩光柵的柵線方程可表示為
φ=nγ1
若n=m+L,γ2=kγ1,則上式可整理為
式中C=Lkγ1.兩光柵線交點的軌跡就是兩根無限長均勻帶電直導線合場強的電場線.
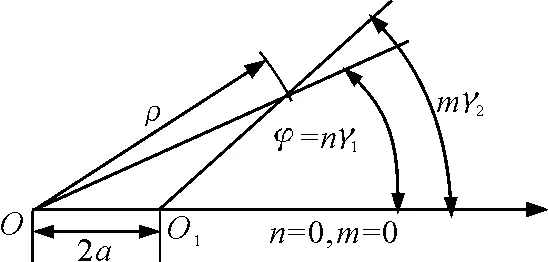
圖2 徑向光柵柵線及其莫爾條紋方程圖解
4數值模擬
利用電腦軟件MathCAD可以對電場線進行數值模擬,如圖3所示.
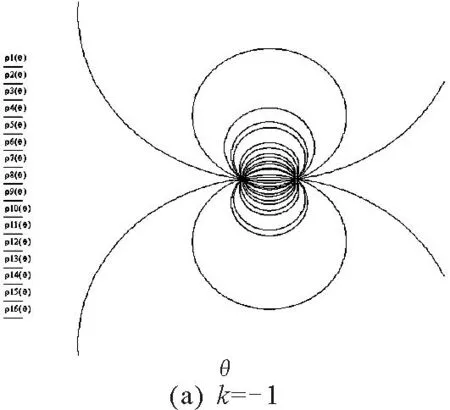


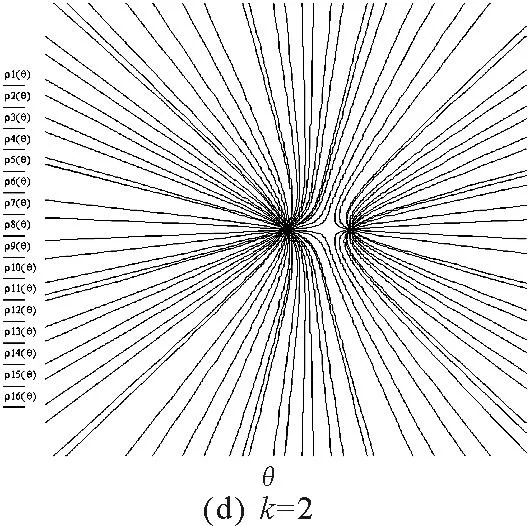
圖3 用MathCAD對電場線進行數值模擬
如圖3(a)所示,當k=-1時表示兩根帶等量異種電荷的無限長直導線的電場線,它們是圓簇;
如圖3(b)所示,當k=1時表示兩根帶等量同種電荷的無限長直導線的電場線,它們是雙曲線簇;
如圖3(c)所示,當k=-2時表示兩根帶不等量異種電荷的無限長直導線的電場線,它們是一種特殊平面曲線簇;
如圖3(d)所示,當k=2時表示兩根帶不等量同種電荷的無限長直導線的電場線,它們是一種特殊平面曲線簇.
5結語
參 考 文 獻
1王小林.兩無限長均勻帶電平行直線的電力線和等位面.西華師范大學學報(自然科學版),2001,22(2):134~138
2徐斌富,章可欽,鄒勇,潘傳芳 .大學物理基礎(第二冊).北京:科學出版社,2007.19~20
3程若磊.無限長均勻帶電線與非接地帶電圓柱導體系統的等勢線與電場線方程 .物理通報,2013(8):22~23
4周城壁.高等數學(第一冊 第三版).北京:高等教育出版社,1997.369
5姚景風.圓光柵的莫爾條紋 .上海機械學院學報,1983(3):77~82
6李治林,劉建科.利用莫爾條紋模擬疊加靜電場的等勢線 .大學物理,2011(6)
Two Deductive Methods on Electric Field Line Equation
of Two Infinite Long Uniformly Charged Wires
Jiang Fujin
(Huangpi No.1 High School, Wuhan, Hubei430300)
Abstract:We obtain the electric field line equation by two infinite long uniformly charged wires with the approach of analytic function, and then deduce the equation by using of the moire fringe of radial circular grating. At last, we do numerical simulation for the electric field line by the software MathCAD.
Key words: analytic function; moire fringe; numerical simulation


