無源雷達天線副瓣對雜波對消的影響分析?

柴致海,呂曉德,楊鵬程,劉 宇,張 丹

(1.中國科學院電子學研究所,北京100190;2.微波成像技術國家重點實驗室,北京100190; 3.中國科學院大學,北京100049)

0 引言

外輻射源雷達是一種間接利用第三方非合作輻射源作為照射源的雙/多基地雷達,常用的信號包括數字電視、調頻廣播和全球移動通信系統(GSM)等[1-4]。由于該體制雷達具有隱蔽性好、抗干擾能力強、成本低及電磁兼容性好等一系列優點[5],受到了國內外的廣泛關注,近年來已成為研究熱點,而雜波對消是研究的熱點問題之一[6-7]。在外輻射源雷達中,相控陣體制雷達具有波束控制靈活、觀測范圍更廣、抗干擾能力更強的優點[8]。

由于參考信號通過參考天線主瓣進入,直達波及多徑雜波通過回波天線的旁瓣進入,而參考天線主瓣與回波天線旁瓣的頻率特性有差異,造成兩路通道接收的信號相關性降低,影響雜波對消,進而影響目標檢測性能[9]。文獻[10]指出,天線旁瓣特性方向圖近似服從正弦分布,以2π為模的話,當信號在π/4附近進入旁瓣時,由于天線旁瓣的特性影響,會使得整個系統的頻率特性發生嚴重的畸變,這說明信號從不同角度進入旁瓣,其受到的旁瓣頻率特性影響也不同,這也是導致信號去相關的原因。而信號的相關性不同在對消時其對應的對消能力也不同。文獻[9]提到,信號帶寬越寬,天線旁瓣的傳輸特性對信號影響越大,同時直達波和多徑雜波受天線方向圖影響,且回波天線轉動時,幅度起伏變化快,雜波頻譜展寬會造成參考信號和干擾信號的相關系數和雜波對消比下降。

為了分析天線旁瓣特性對參考天線和回波天線接收的信號相關性的影響,本文采用天線波束合成來進行仿真分析,通過推導空域濾波器的數學表達式,對在陣元間無幅相誤差時,入射角度不同時信號的相關性不同進行解釋。考慮通道間幅相誤差[11]對相關性的影響,以實例仿真分析并給出一些對零陷、指向影響的規律性結論。同時根據仿真結果,給出一些規律性的結論,為實際無源雷達系統設計及布站提供參考。為研究方便,天線接收的信號僅考慮直達波干擾。

1 信號理論模型分析

本節采用天線波束合成的方法來推導空域濾波器的數學表達式,求出信號經過天線主瓣、旁瓣后的互相關系數ρ,并由此分析天線的旁瓣特性引起主瓣、旁瓣產生去相關效應,從而導致兩通道對消能力的下降。

采用陣元M的均勻線列陣[12-13],陣元間隔d=λ/2,中心頻率為f0,帶寬為B,方位角θ為入射方向與法線方向的夾角,θ∈[-90°,90°],其中θ=0°時為法線方向。陣元接收信號原理圖如圖1所示。

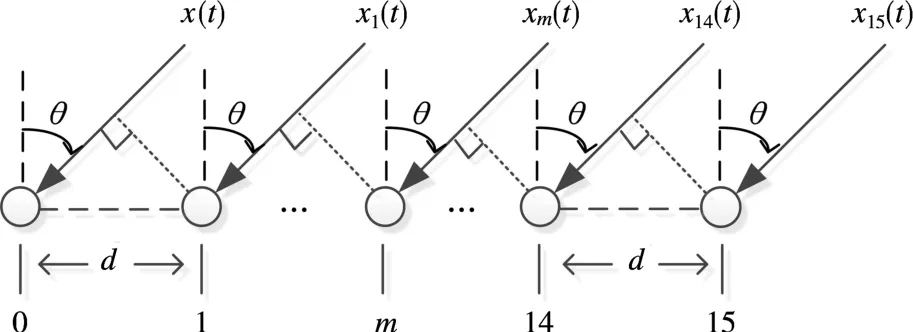
圖1 陣元接收信號原理圖

將第0個陣元作為參考點,則第m個陣元相比于參考陣元的加權系數為e-j2πmdsinθ/λ。

假設陣列輸入信號x(t)是單頻信號ej2πft,入射方向如圖1所示,陣元間距d=λ/2,則陣列輸出信號為

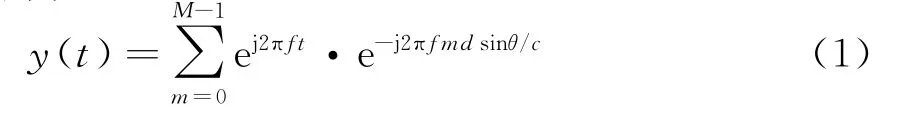
在外輻射源雷達中,輸入信號具有一定的帶寬,可表示為

式中,x0(t)為基帶信號,fc為載波頻率。

式(2)可以改寫為

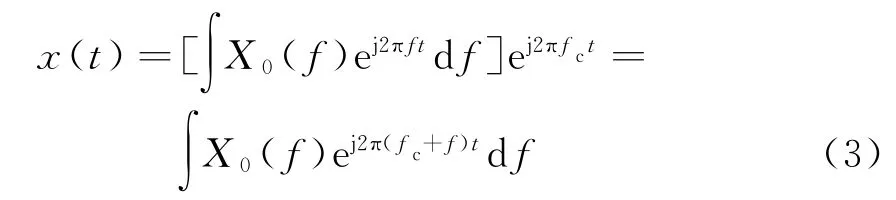
式中,X0(f)為x0(t)的頻譜,X(f)=X0(f-fc)。根據式(2)、式(3),陣列輸出為

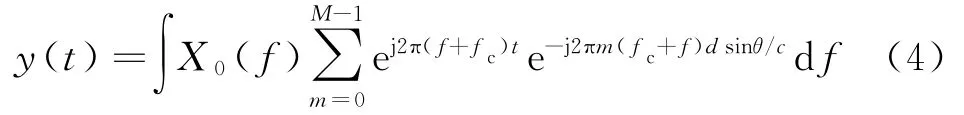
式(4)可轉化為

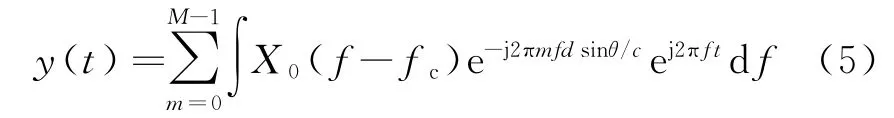
將式(5)變換到頻域,則

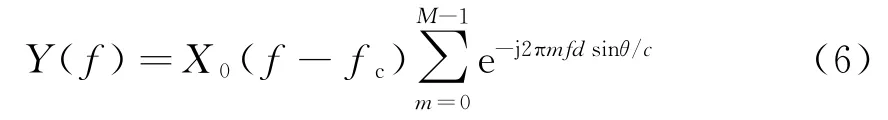
由于均勻線列陣波束形成本身相當于一個空域濾波器H(f,θ),已知輸入信號X(f)和輸出信號Y(f),可得空域濾波器表達式:

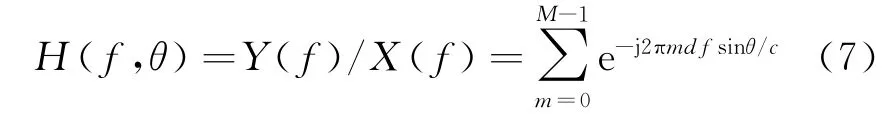
由式(7)可知,對于不同的方位角θ,由于f具有一定的帶寬,所以空域濾波器H(f,θ)對不同角度的信號濾波效果不一樣,相當于不同入射方向的信號經過了不同的濾波器。圖2為θ取不同角度時對應的空域濾波器圖。這也是在無幅相誤差時對不同角度的信號其相關性不同的原因。對于陣列天線波束形成的各旁瓣,其特性在對應的位置與文獻[10]中類似,會引起去相關效應。

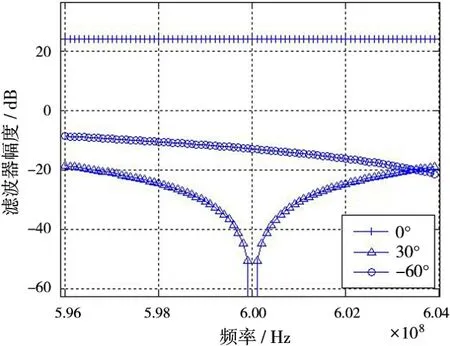
圖2 θ取不同角度時對應的空域濾波器圖

設輸入參考信號功率譜S(f)=1,參考天線的主瓣傳輸函數H1(f)=1,回波天線副瓣傳輸函數為H2(f),此時H2(f)=H(f,θ),則輸入的參考信號與輸出回波信號的互相關系數定義[9]為

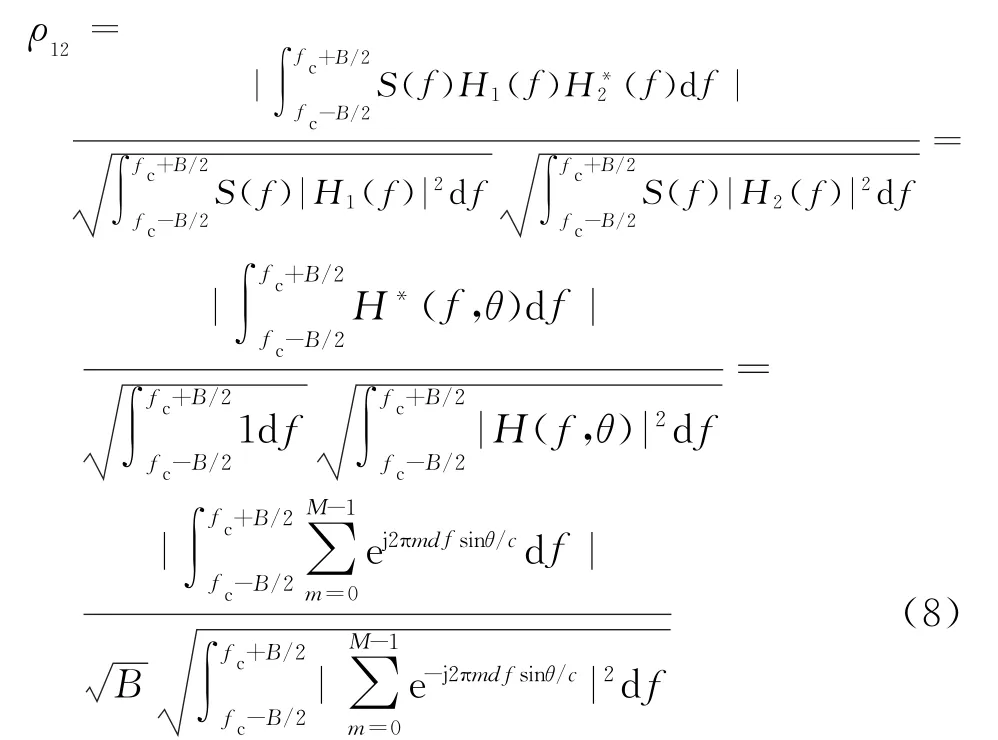
式(9)為陣列天線方向圖,其中d=λ/2,θ∈[-90°,90°]。其歸一化方向圖如圖3所示。

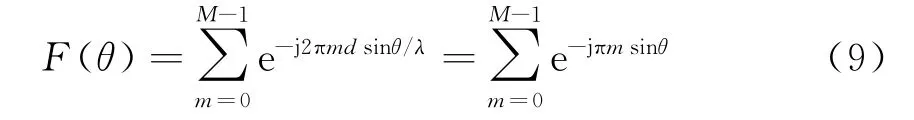
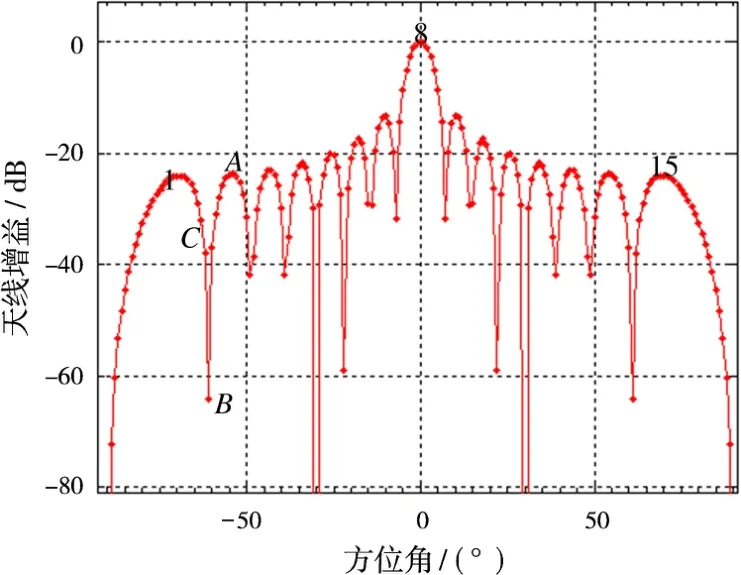
圖3 陣列天線歸一化方向圖

2 陣列天線加權帶來的問題

2.1 無幅相誤差

假設天線陣元理想,無幅相誤差,仿真中采用陣元M=16的均勻線列陣,陣元間隔d=λ/2,中心頻率f0為600 M Hz,帶寬B為8 M Hz,方位角度為θ,θ∈[-90°,90°]。設回波天線中雜噪比為40 d B,參考信號為大信噪比條件,圖4表示信號從θ∈[-80°,80°]進入回波天線時與參考天線接收到信號的互相關系數。圖5為采用傳統的LMS對消時的對消比隨直達波干擾信號入射角度的變化情況。

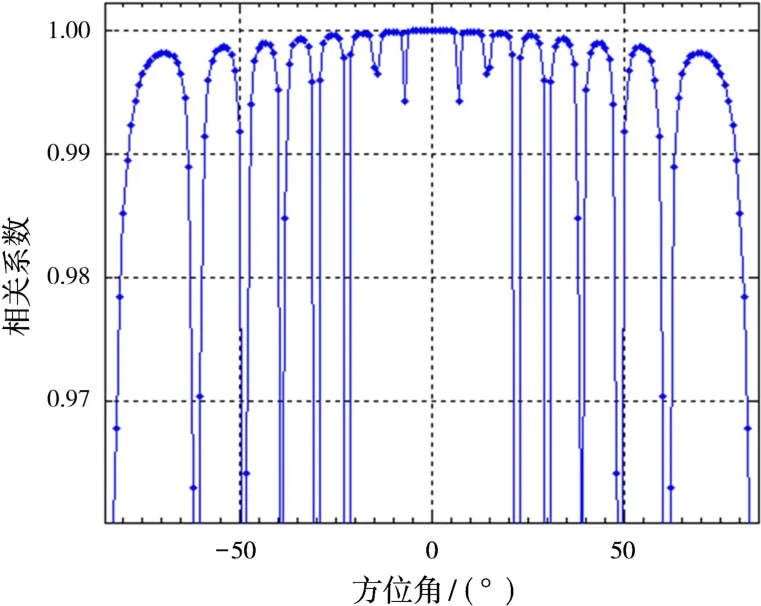
圖4 相關系數隨角度的變化關系

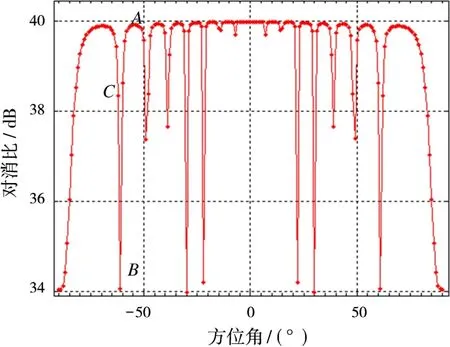
圖5 對消比隨直達波干擾入射角度的變化情況

由圖3～圖5可以得出以下結論:1)相關系數和對消性能隨天線方向圖呈規律變化;2)若將16個陣元形成的15個波束依次命名為旁瓣1、旁瓣2、旁瓣3、……、旁瓣15(其中8為主瓣),如圖4所示,以旁瓣2為例,當直達波干擾按圖4標記位置進入旁瓣時,若從A點進入,旁瓣頻率特性較平坦,對消比相對于主瓣下降不明顯;當直達波干擾從B點進入時,旁瓣頻率特性雖變化劇烈,對消比相比于主瓣下降嚴重,但由于其相當于方向圖的零陷,干擾作用很弱,故不考慮其變化;若直達波干擾從C點及其附近進入時,對消比下降較嚴重,根據方向圖各旁瓣C點位置不同,對消比下降也不相同,嚴重角度能達到約4 d B;3)由于旁瓣只在特定位置附近會導致對消比下降,相比于整個旁瓣寬度只占很小寬度,可以發現,旁瓣寬度越窄,旁瓣導致的對消比下降越不容易體現;4)從實際應用來說,應盡量避免直達波干擾偏離副瓣峰值法線方向進入。

本文中,定義法線方向為0°,改變法線方向,可以得到不同指向的波束,以法線方向為30°為例,如圖6所示,表示的是法線方向為30°時陣列天線歸一化方向圖。若固定干擾入射角為30°,令波束指向在[-90°,90°]間變化,圖7表示的是干擾入射角為30°時的相關系數隨波束指向的變化關系,圖8表示的是干擾入射角為30°時對消比隨波束指向的變化情況。從圖7及圖8可知,干擾入射角偏離波束指向的程度不同,對消性能也不相同。為了使系統對干擾信號抑制性能最佳,應使干擾指向合成波束的B點或A點及其附近,僅可能遠離C點及其附近。同時應盡量避免干擾偏離副瓣峰值法線方向進入。

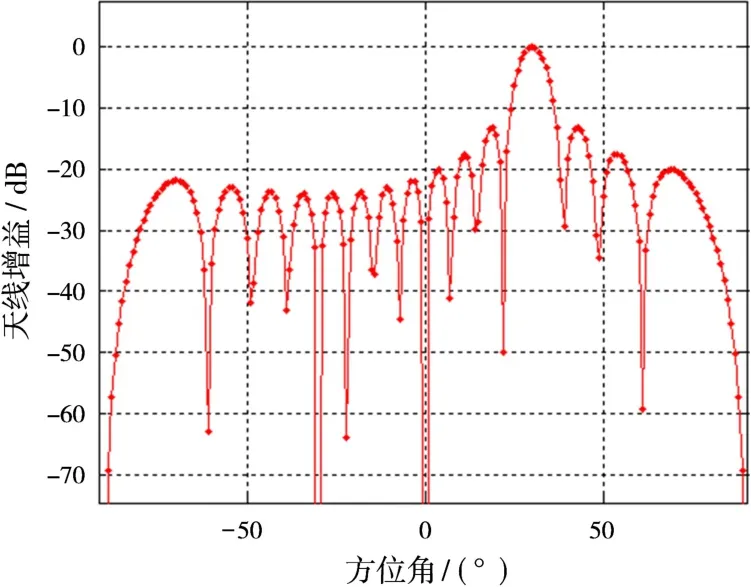
圖6 法線方向為30°時陣列天線歸一化方向圖

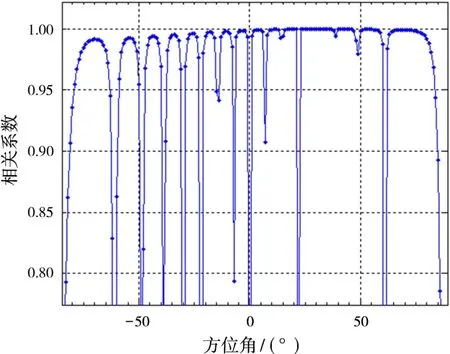
圖7 干擾入射角為30°時相關系數隨波束指向的變化關系

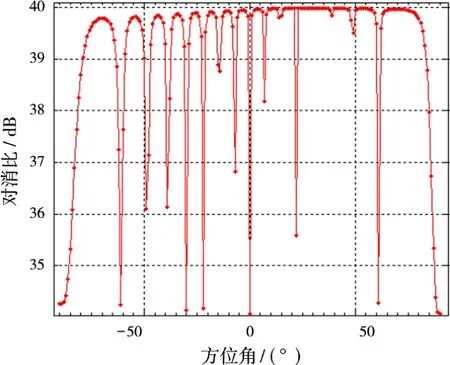
圖8 干擾入射角為30°時對消比隨波束指向的變化情況

2.2 有幅相誤差

在實際情況中,陣元之間必然存在幅相誤差,設在帶內增加幅度誤差服從均值u、標準差σ的高斯分布N(μ,σ2),相位誤差服從均勻分布U[a,b]。參數設置為陣元數M=16,陣元間隔d=λ/2,中心頻率f0=600 M Hz,帶寬B=8 M Hz,方位角度為θ,θ∈[-90°,90°]。設回波天線中雜噪比為40 d B,參考天線為大信噪比條件,增加服從高斯分布的幅度誤差、均勻分布的相位誤差,其概率密度函數分別如式(10)、式(11)所示。其中μ=1,σ=0.115 4,a=-5°,

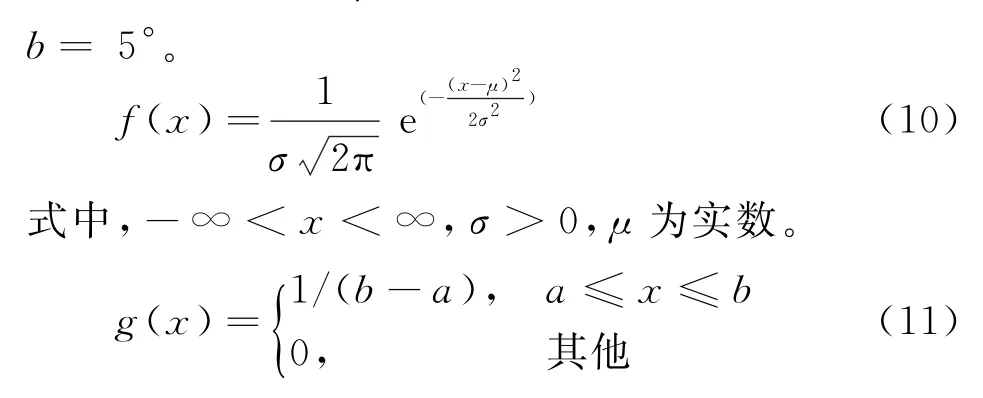
式中,a＜b且a,b均為常數。

圖9是陣元有幅相誤差與無幅相誤差時的天線歸一化方向圖,從圖中可以看出,增加幅相誤差后,會導致方向圖零陷的上升和偏移,進而影響各角度的相關系數及對消比。圖10為回波信號與參考信號的互相關系數隨角度的變化關系。圖11為采用傳統的LMS對消時的對消比隨直達波干擾信號入射角度的變化情況。圖12為對消比隨角度變化時與幅相誤差的關系。

與陣元間無幅相誤差相比,有幅相誤差時,由圖9～圖12,可得如下結論:1)相關系數和對消性能隨天線方向圖規律變化;2)僅當直達波干擾從方向圖C點及其附近進入時,對消比下降較嚴重,根據方向圖各旁瓣C點位置不同,對消比下降也不相同,且在偏離方向圖法線位置對消比下降不如無幅相誤差嚴重;3)可以發現,旁瓣寬度越窄,旁瓣導致的對消比下降越不容易體現;4)由于方向圖零陷的上升和偏移,甚至有些地方旁瓣的A點變成了B點,旁瓣的個數也在變化,幅相誤差越大,方向圖畸變越嚴重。從實際應用來說,幅相誤差的增加會導致方向圖的畸變,且具有隨機性,不利于選取最佳接收信號的方向,故應減小陣元間的幅相誤差的變化范圍。

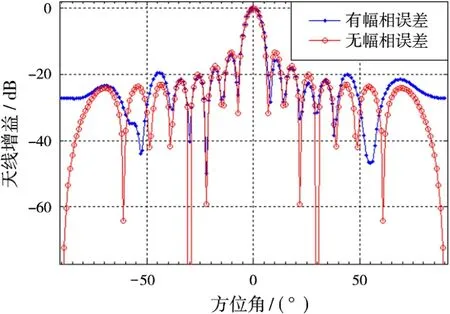
圖9 陣元有幅相誤差與無幅相誤差時的天線歸一化方向圖

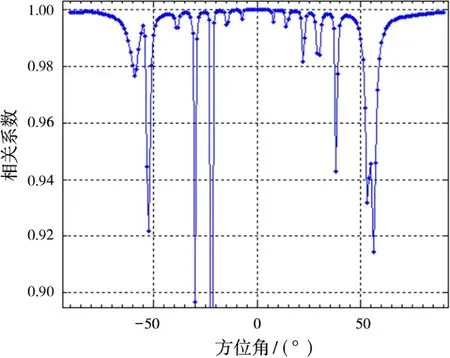
圖10 回波信號與參考信號的互相關系數隨角度的變化關系

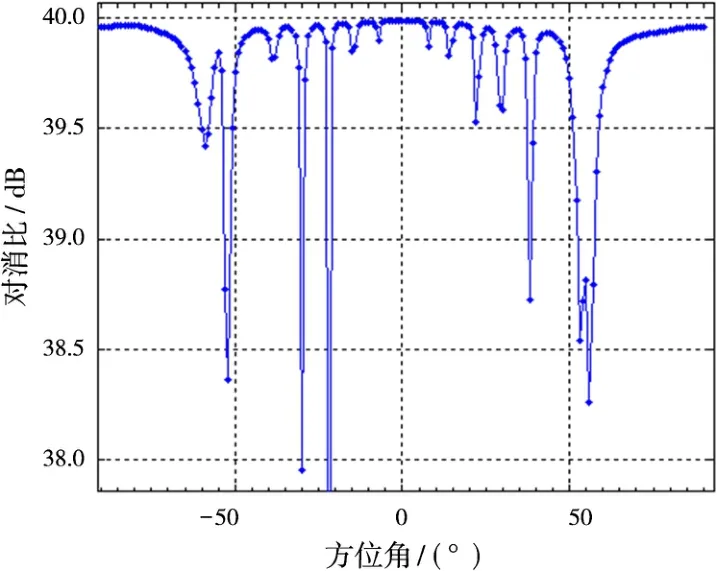
圖11 對消比隨直達波干擾入射角度的變化情況

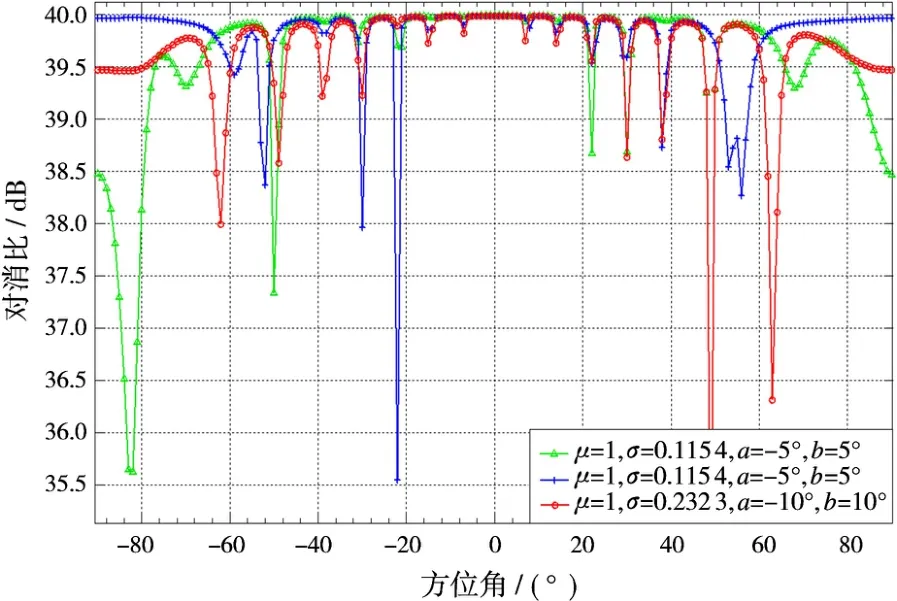
圖12 對消比隨角度變化時與幅相誤差的關系

3 結束語

本文采用天線波束合成的方法分析空域濾波器H(f,θ),由于其特性在可見域內不僅隨頻率f變化,而且隨入射角θ變化,即在不同角度其濾波效果不同,由此分析了通道間有無幅相誤差條件下對直達波及多徑的對消效果;在無誤差條件,入射方向不同時信號的相關性不同,引起對消性能發生變化。極端情況下會導致對消比惡化約4 dB。在幅度誤差服從均值μ=1、標準差σ=0.1154的高斯分布,相位誤差服從均勻分布U[-5°,+5°]的誤差條件下,方向圖的空域濾波性能變差,包括零陷升高或偏移,甚至旁瓣由峰值變為零陷,旁瓣的個數發生變化等,從而進一步引起輸入輸出信號產生去相關效應。

根據以上分析結果認為:

1)由于副瓣去相關效應,主天線接收不同方向的直達波及雜波,對消性能會有所變化,當直達波干擾從方向圖旁瓣的C點及其附近進入時,對消比下降最為嚴重;

2)有誤差影響時,零陷升高或偏移,甚至旁瓣由峰值變為零陷,旁瓣的個數發生變化等,從而進一步引起輸入輸出信號產生去相關效應;

3)在應用方面,以上分析說明應盡量避免直達波干擾處于C點區域,但實際很難實現。可行的解決辦法是采取陣列波束加權的方法抑制副瓣。另外,幅相誤差的增加會導致方向圖的畸變,不利于自適應波束合成及最佳接收方向選擇,故系統設計中應控制陣元間的幅相誤差。以上工作可作為波束賦形及無源雷達布站設計的參考。

[1]GRIFFITHS H D,BAKER C J.Passive Coherent Location Radar Systems.Part 1:Performance Prediction [J].IEE Proceedings—Radar,Sonar and Navigation, 2005,152(3):153-159.

[2]LU X,LI J,LIN K,et al.Range-Doppler NLMS (RDNLMS)Algorithm for Cancellation of Strong Moving Targets in Passive Coherent Location(PCL) Radar[C]∥IEEE International Radar Conference, Lille,France:IEEE,2014:1-5.

[3]李紀傳,呂曉德,向茂生,等.等效凹槽濾波器及其在無源相關定位雷達中的應用[J].雷達學報,2014,3 (6):675-685.

[4]楊鵬程,呂曉德,李紀傳,等.基于壓縮感知的外輻射源雷達目標檢測[J].雷達科學與技術,2015,13(4): 384-389. YANG Pengcheng,LYU Xiaode,LI Jichuan,et al. Target Detection for Passive Radar Using Compressive Sensing[J].Radar Science and Technology,2015,13 (4):384-389.(in Chinese)

[5]萬顯榮.基于低頻段數字廣播電視信號的外輻射源雷達發展現狀與趨勢[J].雷達學報,2012,1(2):109-123.

[6]ZHAI Y,WU J.A Clutter Cancellation Method in Passive Radar Based on MUSIC Time Delay Estimation [C]∥IEEE International Conference on Computer and Communications,London,UK:IEEE,2015:347-351.

[7]張各各,王俊,劉玉春.一種基于數字電視地面廣播照射源的外輻射源雷達快速雜波相消算法[J].電子與信息學報,2013,35(1):36-40.

[8]ROSHANZAMIR A S,BASTANI M H.Phased Array Radar Beamforming Method Based on MIMO Radar Covariance[C]∥IET International Radar Conference,Hangzhou:IET,2013:1-6.

[9]馮遠.數字電視輻射源雷達參考信號獲取及干擾抑制算法研究[D].北京:北京理工大學,2014.

[10]保錚.自適應天線旁瓣相消的幾個主要問題[J].西北電訊工程學院學報,1980(4):1-17.

[11]袁自月,牛一鳴,楊國,等.一種陣列天線陣元幅相、位置誤差校正方法[J].電子與信息學報,2014,36 (9):2232-2237.

[12]ZHANG Y D,AMIN M G,AHMAD F,et al.DOA Estimation Using a Sparse Uniform Linear Array with Two CW Signals of Co-Prime Frequencies[C]∥ IEEE International Workshop on Computational Advances in Multi-Sensor Adaptive Processing,Saint Martin,French West Indies:IEEE,2013:404-407.

[13]HSIAO P C,LIN Y T,CHEN S G.An Efficient Searching Algorithm for High DoF Non-Uniform Linear Antenna Array with Constrained Spacing[C]∥13th International Conference on Telecommunications,Graz,Austria:IEEE,2015:1-5.