城市噪聲監測優化布點研究

錢琪所 ，林秀珠

(1. 云南省環境工程評估中心，云南 昆明 650032；2. 福建師范大學福清分校，福建 福清 350300)

城市噪聲監測優化布點研究

錢琪所1，林秀珠2

(1. 云南省環境工程評估中心，云南 昆明 650032；2. 福建師范大學福清分校，福建 福清 350300)

摘要：為探討城市以較少網格監測點獲得較科學的聲環境信息，分析區域環境噪聲監測點的優化問題，減少每年監測帶來的巨大工作量。在借鑒國內噪聲監測優化布點研究成果的基礎上，結合環境噪聲污染特征，以福建省某城市為例，運用物元分析法和熵權法確定最優測點數，把該市區域環境噪聲普查的152個監測點位優化為12個。將此方法與統計分析方法作比較，經驗證，兩種方法監測的等效聲級和標準差平均值均<2dB(A)，監測結果之間無顯著性差異

關鍵詞：城市噪聲監測；優化布點；物元分析；熵權法；統計分析法

0引言

城市區域環境噪聲監測作為環境監測體系的一個重要組成部分，噪聲監測布點的合理性關系到能否客觀、準確地反映城市噪聲環境質量。城市環境噪聲監測優化布點研究的一個重要內容就是用較少的監測點位來反映整個城市的噪聲水平。為了解決城市噪聲監測的實際問題，須選取一個或多個能代表整個城市建成區環境噪聲平均水平的測點，進行長期噪聲定點在線監測。國內外學者對優化布點工作進行了大量的研究[1-5]。

本研究以福建省某城市網格布點法實測數據為例，以物元分析法和熵權法確定最優測點數，并將其結果與統計分析方法作比較。

1物元模型相關理論[6-9]

1.1理想點和期望點

對某一監測點位的各項指標實測值進行比較，選擇出各項指標測值的最大值和最小值。對于越大越好型指標，其最小值和最大值分別構成“最佳理想點”a(最小值)和“最次理想點”b(最大值)，并取各項指標實測值的平均值構成“期望點”c(均值)。

1.2構建標準物元矩陣和節域物元矩陣

由“期望點”c分別與“最佳理想點”a和“最次理想點”b構成兩個標準物元矩陣：

(1)

(2)

由a、b兩點組成的事物，其各項指標數值的范圍相比較標準事物數值的范圍擴大化了，其量值范圍組成節域事物的物元矩陣：

(3)

式中：M 表示事物；Qj表示關于M事物的第j個評價指標。

1.3物元矩陣的構建

將每個監測點位作為一個事物，其指標的監測值構成一個物元矩陣：

(4)

式中：xij(i=1，2，……，n； j=1，2，……，m)為第i個點第j項污染指標值。

1.4熵權法賦權

為了避免人為因素的干擾，在確定權重時，采用Shannon法，從指標實測數據入手，利用數據自身信息，客觀賦權。其具體步驟如下：

(1)初始矩陣的構建

設有n個評價對象，每個評價對象有m個指標，則第i個評價對象第j個指標記為xij，其形成初始矩陣：

(5)

(2)構建標準化矩陣

利用指標不同屬性，可將評價指標分為正向型指標和負向型指標。因此，在確定各指標權重之前，需要先對每個樣本進行歸一化處理，具體方法如下：

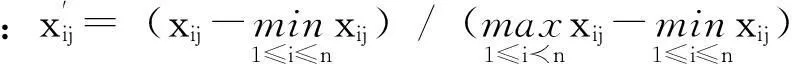
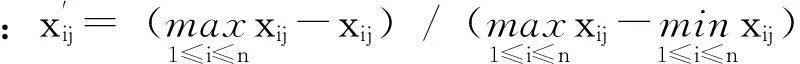
(6)

從而得到標準化矩陣：

(7)

(3) 熵的確定

設第j個指標第i個評價點的評價指標比重為：

(8)

則第j個評價指標的熵為：

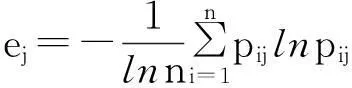
(9)

(4)熵權的確定

第j個評價指標的權重為：

(10)

1.5構建關聯函數

根據節域物元矩陣和標準物元矩陣，分別構建待優化物元與標準物元之間的關聯函數Ka(xij)、Kb(xij)以及綜合關聯函數Ka(xi)、Kb(xi)。以Ka(xi)、Kb(xi)為坐標軸，做出待優化斷面的聚點圖。根據圖中點的分布，結合實際情況進行優化。

各單項環境污染因子對“最佳”和“最次”理想點的關聯函數值為：

Ka(xij)=(xij-cj)/(cj-aj)

(11)

綜合關聯函數為：

(12)

2實例分析

2.1選擇理想點和期望點

以福建省某城市的環境噪聲監測數據為例，最后3行列出了“最佳理想點a”、“最次理想點b”和“數學期望點c”的數據，具體監測數據見表1。根據式(1)、式(2)、式(3)及表1中的數據，分別構建標準物元矩陣和節域矩陣：

2.2構建物元矩陣

根據式(4)和表1分別寫出各個噪聲測點的物元矩陣，限于篇幅，只給出1號測點的物元矩陣：

2.3熵權法賦權

2.3.1構建初始矩陣

根據表1的數據，形成初始矩陣：

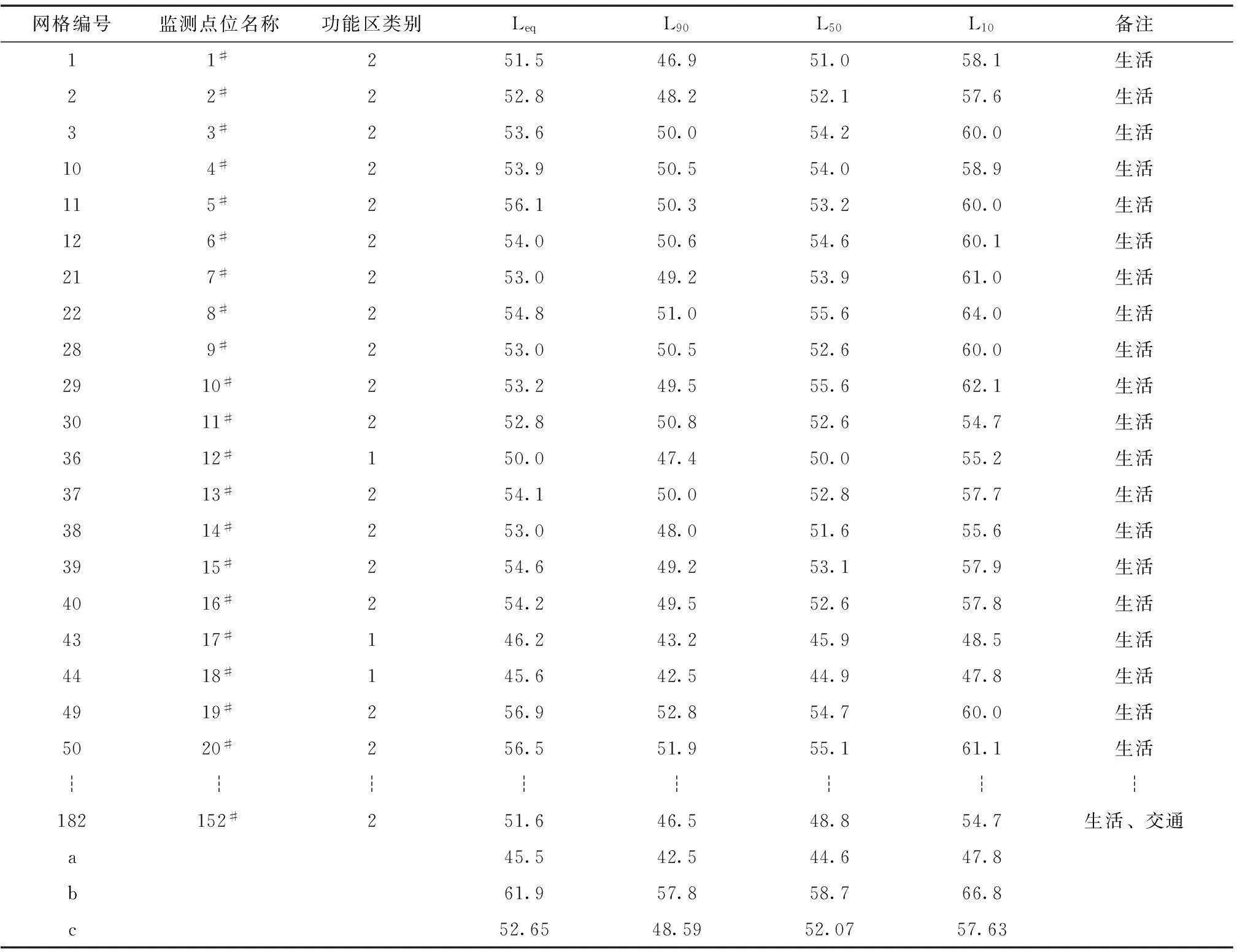
表1　福建省某城市噪聲監測數據

2.3.2矩陣標準化

根據環境噪聲的屬性，判斷其評價指標為負向型指標。因此，根據式(6)的負向型指標對每個樣本進行歸一化處理，從而得到標準化矩陣：

2.3.3權重系數的確定

根據熵權法確定指標權重，結果見表2。

2.4關聯函數的確定

據式(11)、式(12)測算綜合關聯函數值，結果見表3。以Ka、Kb為坐標軸，分別作出各監測點位的點聚圖，如圖1所示。

由圖1可見，幾乎所有的監測點都分布在Ⅱ、Ⅳ兩個象限內。其中，Ⅱ象限內的點符合最劣點條件，Ⅳ象限內的點符合最佳點條件。靠近原點的點在一定條件下可以向第Ⅱ象限、Ⅳ象限轉化。本研究采用的點位分類方法是：計算所有點位與原點之間的距離r。在同一象限內，r≤0.2的點位歸為同一類監測點，0.21的點位為同一類監測點。根據此方法的計算結果，所有監測點可分為十二類，見表4。

表2　各指標熵值與熵權

表3　綜合關聯函數結果

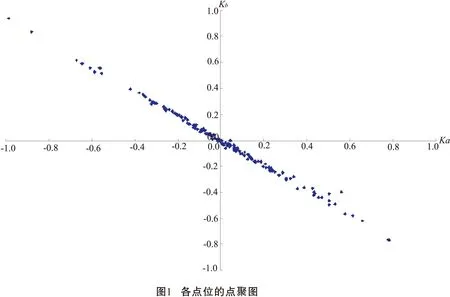
表4　各點位的分類結果類別點位距離平均值優選點位一

類別點位距離平均值優選點位一1、2、38、54、55、93、100、103、128、140、144、170、171、172、177、180、185、41、45、133、99、122、147、187、121、67、71、75、79、83、1150.100945二36、107、135、156、160、173、179、33、48、95、138、24、146、183、42、96、101、1230.2914156三69、130、131、137、184、25、178、4、52、116、1820.46914四53、70、150、1570.758070五118、158、1140.8620114六43、441.307444七30、37、39、40、51、61、62、63、68、89、105、117、120、136、143、174、175、176、47、91、110、139、106、134、31、73、74、80、81、102、112、113、126、127、1810.0919181八3、10、11、21、28、60、78、104、132、19、20、32、65、72、88、108、125、186、5、15、92、77、1290.293620九12、29、49、50、56、97、23、76、1090.484229十22、57、13、85、86、98、111、6、640.660098十一66、140.856614十二87、1241.094887

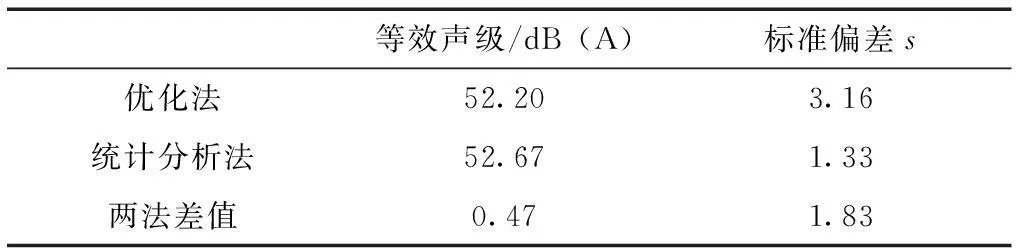
表5　各功能區優化點位表

注：( )內數字為監測點編碼。

2.5確定優化點位

對監測點位的選擇方法，大致可分為3種[10-12]：選擇符合程度較高的點作為優選點；選擇符合程度最高和最不穩定有可能轉化的點位為優選點；將分布相對集中的點進行分類，選擇其中符合程度最高的點作為該類點的代表。

以上3種方法都具有一定合理性，文獻[13]在上述方法的基礎上有所改進。本研究直接采用文獻[13]的方法來選擇監測點位。步驟如下：①計算所有的點與原點之間的距離r；②計算這些距離的平均值；③選取最接近該平均值的點作為該類別的優選點。

由表6可見，優化法和統計分析法的噪聲等效聲級平均值相差不大，僅為0.47dB(A)，標準偏差值也僅為1.83dB(A)。

3結果檢驗

3.1t檢驗模型[14]

為了檢驗優化出的點位是否能夠代表該區域環境噪聲的總體水平，本研究采用“t檢驗”法對優化點位平均值與統計分析平均值進行比較。

式中：μ0為優化法Leq值；μ為統計分析法Leq值；n為優選點數；s為優化法S值。

3.2t檢驗結果

假設H0：μ=μ0，根據公式(13)計算 t 值，確定α= 0.05，根據自由度v= n-1，從 t 值表查出 t0. 05(n′)的界限值，檢驗結果列于表7。

表7　t檢驗結果

由表7可知，該城市各功能區及全市計算出的t值均

4結論與建議

(1)通過對城市區域環境噪聲普查優化布點進行研究分析，采用了一種簡單、快速、經濟、實用的城市噪聲監測優化布點方法，既能代表整個城市區域環境噪聲的總體水平，又能代表城市不同區域的環境噪聲水平。同時，優化出的點位比較均勻地分布在全市范圍內，覆蓋了全市各個不同環境噪聲水平的小區域，能比較真實可靠地監控全市的環境噪聲污染水平。

(2)優選測點的位置兼顧了聲源、環境敏感點等多種因素，具有較好的代表性[15]。

(3)利用物元分析理論和熵權法選取最佳點位對城市區域環境噪聲進行優化布點，既能有效地反映城市聲環境質量，滿足國家規范要求，又能節省大量人力、物力，有利于監測水平的提高和城市聲環境的管理。

(4)將優化結果與統計分析方法進行比較，兩種方法具有相同的精密度，均無顯著性差異，結果滿意。

參考文獻：

[1]馬東升,趙廣宇.灰色關聯度分析法在環境噪聲監測優化布點上的應用[J].遼寧城鄉環境科技, 1998,18(2):1-2.

[2] 莊世堅,高誠鐵,歐壽銘,等.用主成分子集合選擇法優選大氣環境測點[J].中國環境科學, 1990,l0(2):148.

[3] 許榕.大氣環境監測優化布點的研究[J].中國環境監測, 1994,10(5):1-2.

[4] 朱雨,賴世強,黃克勝,等.溫州市大氣環境監測優化布點的研究[J].環境污染與防治,1989,11(2):7-8.

[5] 韓玉成,楊光宇,張克偉.模糊數學在大氣優化布點方面的應用[J].中國環境監測,1988,4(4):1-2.

[6] 蔡文.物元分析[M].廣州:廣東高等教育出版社,1987.

[7] 蔡文.物元模型及其應用[M].北京:科學技術文獻出版社,1994:2-8.

[8] 張勇,黎雪梅.物元分析在環境質量評價及優化布點的應用[J].環境科學與技術,2005,28(s1):114-16．

[9] 饒清華,張江山.熵權物元分析模型在湖泊富營養化評價中的應用[J].環境工程,2006,24(6):80-83.

[10] 李祚泳.環境監測優化布點的物元分析模型[J].環境工程,1996,14(3):46-49.

[11] 孫中黨,畢雪玲,康莉萍,等.物元分析法在鄭州市大氣監測優化布點中的應用[J].河南科學,1999,17(2):194-99．

[12] 高明慧.用物元分析法進行水質環境監測優化布點的研究[J].環境科學進展,1997,5(3):77-81.

[13] 林鴻雁,張江山,林少玲,等.熵權物元分析法在輻射環境監測優化布點中的應用[J].環境監測管理與技術,2009,10,21(5):1-4.

[14] 侯天蘭.應用統計分析方法優化布點監測區域環境噪聲[J].環境監測管理與技術,2004,16(5):2-3.

[15] 周鳳.區域環境噪聲監測優化布點研究[J].環境科學動態,2003,7(2):7-9.

Research on Optimization of Urban Noise Monitoring Site

QIAN Qi-suo1, LIN Xiu-zhu2

(1. Yunnan Provincial Center for Environmental Engineering, Kunming Yunnan 650032, China)

Abstract：In order to get more scientific acoustic environmental information with less monitoring sites, the optimization of noise monitoring sites of the urban area was analyzed. Based on the current results of optimizing the noise monitoring sites combining with the characteristics of noise pollution in China, Fuqing city was studied as a case. The 152 monitoring points were optimized to 12 using the substance element analysis and coefficient of entropy. Comparing the method with the statistical analysis method, the equivalent sound level and standard deviation of the two methods are all less 2 dB(A). Therefore, there was no significant difference between these two methods.

Key words：noise monitoring; optimization; urban noise; matter element analysis; statistical analysis

歡迎訂閱

中圖分類號：X839.1

文獻標志碼：A

文章編號：1673-9655(2015)04-0112-06

作者簡介：錢琪所(1979-)，男，工程師。

收稿日期：2015-03-02