一次奇怪的網(wǎng)絡(luò)故障
■ 浙江 盛建平
編者按: 筆者遇到某單位進(jìn)行網(wǎng)絡(luò)改造后,由于網(wǎng)絡(luò)變動觸發(fā)應(yīng)用的隱性Bug,最后由開發(fā)部門與網(wǎng)絡(luò)部門合作解決,該故障在日常非常罕見,因此進(jìn)行了總結(jié)。
某單位外聯(lián)網(wǎng)絡(luò)為二層架構(gòu),外部用戶訪問內(nèi)部通迅機(jī),使用防火墻進(jìn)行端口級保護(hù)。但二層架構(gòu)安全性不高,內(nèi)部通迅機(jī)直接暴露給外部用戶,若通迅機(jī)被攻破,則可能直接進(jìn)入內(nèi)網(wǎng),對該單位信息系統(tǒng)安全構(gòu)成威脅。
為有效保障網(wǎng)絡(luò)安全,該單位對外聯(lián)網(wǎng)絡(luò)進(jìn)行改造,新增DMZ區(qū),將通迅機(jī)前移到原防火墻外部的DMZ區(qū),并在通迅機(jī)與外部用戶之間新增其他廠商的防火墻實(shí)現(xiàn)異構(gòu)。改造前后拓?fù)淙鐖D1所示。
故障現(xiàn)象
外聯(lián)網(wǎng)絡(luò)從二層架構(gòu)切換到三層架構(gòu)后,外部用戶訪問DMZ區(qū)通迅機(jī)辦理業(yè)務(wù),發(fā)現(xiàn)約有30%的交易不成功,有時重新辦理又會成功,極大的影響了用戶體驗(yàn)。回退到二層架構(gòu),業(yè)務(wù)又都正常。
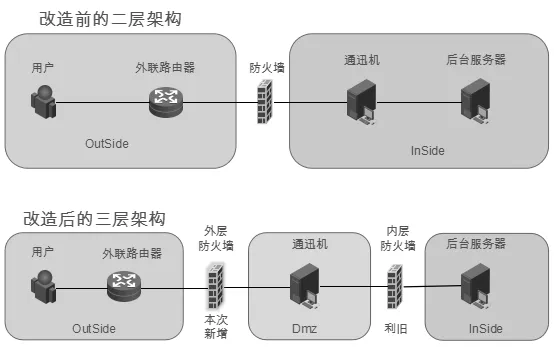
圖1 改造前后的拓?fù)鋱D
故障分析
因通迅機(jī)雖改變了部署位置,但通迅程序未做任何變動,而本次又是新增了不同廠商的防火墻,因此排查重點(diǎn)定位在新增防火墻上。
檢查外層防火墻配置,未發(fā)現(xiàn)異常。使用抓包工具對外層防火墻內(nèi)、外口進(jìn)行抓包分析,看是否存在異常的數(shù)據(jù)包。經(jīng)分析,發(fā)現(xiàn)防火墻內(nèi)、外口數(shù)據(jù)完全一致,并未發(fā)現(xiàn)丟包等異常現(xiàn)象。對業(yè)務(wù)出現(xiàn)異常時的數(shù)據(jù)包進(jìn)行分析,發(fā)現(xiàn)數(shù)據(jù)收發(fā)均正常,見圖2第610-613號數(shù)據(jù)包,客戶端A.100.27發(fā)送了兩個數(shù)據(jù)包(第 610和 612號),服務(wù)端B.231.2回復(fù)了兩個ACK進(jìn)行 確 認(rèn)(第 611和613號)。但奇怪的是,服務(wù)端突然發(fā)送RST報(bào)文中斷了TCP連接,如圖2所示。
在網(wǎng)絡(luò)人員進(jìn)行故障分析的同時,應(yīng)用開發(fā)人員對應(yīng)用日志進(jìn)行了分析。對通迅機(jī)上提取到的日志分析后發(fā)現(xiàn),當(dāng)某筆業(yè)務(wù)不成功時,服務(wù)程序僅接收到1460字節(jié)的數(shù)據(jù),而非第610和612號數(shù)據(jù)包發(fā)送的1584字節(jié)(注:第610號數(shù)據(jù)包長度為1514,減去以太網(wǎng)頭部14字節(jié),IP頭部20字節(jié),TCP頭部20字節(jié),實(shí)際有效數(shù)據(jù)載荷為1460字節(jié),同樣第612號數(shù)據(jù)包有效數(shù)據(jù)載荷為124字節(jié),兩個數(shù)據(jù)包共發(fā)送1584字節(jié))。開發(fā)人員認(rèn)為,服務(wù)程序從網(wǎng)絡(luò)上接收數(shù)據(jù)不完整,導(dǎo)致程序處理異常,應(yīng)用連接中斷,從而引起交易失敗。
問題陷入僵局,從網(wǎng)絡(luò)層面分析,客戶端交易數(shù)據(jù)均已正確發(fā)往服務(wù)端,并收到服務(wù)端的確認(rèn);從應(yīng)用日志分析,服務(wù)端數(shù)據(jù)接收不完整,從而引起交易中斷。就像一起網(wǎng)絡(luò)訂單,前后共發(fā)兩個快遞,快遞公司均已送達(dá)并經(jīng)門衛(wèi)簽收(ACK報(bào)文),但最終用戶從收發(fā)室(緩沖區(qū))只收到第一個快遞(1460字節(jié))。最奇怪的是那個RST報(bào)文,明明數(shù)據(jù)完整送達(dá)了,服務(wù)方卻中止了TCP連接。
重新回顧RST報(bào)文產(chǎn)生原因,主要有如下幾種情況:
一是端口未打開。如A機(jī)向B機(jī)發(fā)送一個SYN請求,表示想連接B機(jī)的3000端口,但B機(jī)上并沒有打開3000端口,于是向A機(jī)發(fā)送了一個RST。
二是請求超時。如A機(jī)的程序建立了Socket之后,用setsockopt的SO_RCVTIMEO選項(xiàng)設(shè)置了recv的超時時間為100ms,若此時A機(jī)發(fā)送SYN后到從B機(jī)接收到SYN的時間超過100ms,則A機(jī)上的程序認(rèn)為接收超時,會發(fā)送RST拒絕進(jìn)一步發(fā)送數(shù)據(jù)。

圖2 服務(wù)端突然發(fā)送RST報(bào)文并中斷了TCP連接
三是提前關(guān)閉。若客戶端向服務(wù)端發(fā)送了2000字節(jié),而服務(wù)端程序僅接收前1800字節(jié)就關(guān)閉了連接,此時TCP層發(fā)現(xiàn)“Close Socket時Recv Buff不為空”,TCP認(rèn)為數(shù)據(jù)沒有正確提交到應(yīng)用,使用RST關(guān)閉連接。表現(xiàn)在抓包信息上就是客戶機(jī)向服務(wù)器發(fā)送了2000個字節(jié)的數(shù)據(jù),然后服務(wù)器端發(fā)送ACK進(jìn)行確認(rèn),緊接著服務(wù)器向客戶機(jī)發(fā)送了一個RST斷開連接,該現(xiàn)象和本案的故障非常相像。
最后一種是在一個已關(guān)閉的Socket上收到數(shù)據(jù)。如客戶端在服務(wù)端已經(jīng)關(guān)閉掉Socket之后,仍然在發(fā)送數(shù)據(jù),這時服務(wù)端會產(chǎn)生RST。
多種解決方案
根據(jù)RST報(bào)文產(chǎn)生的第三個原因,我們提出第一個解決方案,即服務(wù)端在收到1460字節(jié)后,對報(bào)文接收完整性進(jìn)行校驗(yàn),若未全部接收,則繼續(xù)接收剩余的數(shù)據(jù)。據(jù)此開發(fā)人員修改程序后,業(yè)務(wù)回歸正常。(該解決方案由胡瑛提出并實(shí)現(xiàn),在此表示感謝)
根據(jù)網(wǎng)絡(luò)訂單二個快遞的說法,我們猜想若最終用戶稍等片刻再取快遞,是否就能一次性取到完整的二個快遞呢?據(jù)此開發(fā)人員修改程序,從緩沖區(qū)接收數(shù)據(jù)前,先等待2毫秒,之后業(yè)務(wù)也回歸正常。
結(jié)語
本次故障是網(wǎng)絡(luò)變動觸發(fā)應(yīng)用的隱性Bug,實(shí)屬罕見。該問題的解決得益于網(wǎng)絡(luò)與開發(fā)相互配合,通力合作。建議在使用Socket接口接收變長報(bào)文體時,采用尾標(biāo)識法(通過尋找接收的通迅報(bào)文中的尾標(biāo)識字符串,確認(rèn)報(bào)文是否完整)或負(fù)載長度法(通過通迅報(bào)文頭添加報(bào)文長度字段,確定有效報(bào)文的長度)等來提高報(bào)文接收的可靠性和完整性。

