基于 Bayes 法的電主軸極小子樣可靠性研究

第一作者 蔣喜 男，碩士生，1987年生

通信作者 劉宏昭 男，教授，博士生導(dǎo)師，1954年生

基于Bayes法的電主軸極小子樣可靠性研究

蔣喜, 劉宏昭，訾佼佼，原大寧，劉麗蘭

(西安理工大學(xué) 機(jī)械與精密儀器工程學(xué)院，西安710048)

摘要：針對(duì)長(zhǎng)壽命的磨削電主軸極小子樣的可靠性評(píng)估問(wèn)題，提出了Bayes結(jié)合虛擬增廣樣本的分析方法。首先，在Bayes法基本流程的指導(dǎo)下，研究了基于Bayes法的磨削電主軸可靠性評(píng)估方法。根據(jù)定時(shí)截尾試驗(yàn)的原則對(duì)電主軸進(jìn)行可靠性試驗(yàn)，應(yīng)用Bayes法結(jié)合磨削電主軸試驗(yàn)樣本的可靠性試驗(yàn)數(shù)據(jù)，綜合虛擬增廣樣本法對(duì)其可靠性進(jìn)行評(píng)估，最終獲得電主軸的可靠性評(píng)估結(jié)果。最后，將基于Bayes法與基于偽壽命分布法的磨削電主軸極小子樣可靠性評(píng)估結(jié)果進(jìn)行比較，以驗(yàn)證基于Bayes法可靠性評(píng)估理論的合理性。

關(guān)鍵詞：電主軸；極小子樣；Bayes；虛擬增廣；可靠性

基金項(xiàng)目：國(guó)家科技重大專項(xiàng)計(jì)劃資助項(xiàng)目(2010ZX04014-012)；國(guó)家自然科學(xué)基金(51275404)；陜西省自然科學(xué)基金(2012JQ7011)；陜西省重點(diǎn)學(xué)科建設(shè)專項(xiàng)資金資助項(xiàng)目

收稿日期：2013-10-21修改稿收到日期：2014-01-28

中圖分類號(hào):TH133.2文獻(xiàn)標(biāo)志碼： A

Extremely small sample’s reliability of a motorized spindle based on Bayes method

JIANGXi,LIUHong-zhao,ZIJiao-jiao,YUANDa-ning,LIULi-lan(School of Mechanical and Precision Instrument Engineering, Xi’an University of Technology, Xi’an 710048, China)

Abstract:Aiming at the reliability evaluation of a long life grinding motorized spindle’s extremely small sample, a Bayes method combined with virtual augmented sample was proposed. Firstly, under the guidance of the basic process of Bayes method, the reliability evaluation method of a grinding motorized spindle based on Bayes method was studied. According to the principle of timing truncation tests, the reliability tests of the motorized spindle were conducted. Then, Bayes method combined with the reliability testing data of the grinding motorized spindle’s testings sample and the virtual augmented sample method was applied to assess the reliability of the spindle. Furthermore, the reliability evaluation results of the motorized spindle were obtained. Finally, the reliability evaluation results of the grinding motorized spindle based on Bayes method and those based on the false life’s distribution method were compared to verify the correctness of the proposed method.

Key words: motorized spindle; extremely small sample; Bayes; virtual augmented; reliability

磨削電主軸已較為普遍地被應(yīng)用于數(shù)控加工中心，以實(shí)現(xiàn)機(jī)械加工的高速化和超精密化。作為數(shù)控加工中心的核心部件，磨削電主軸可靠性就成為了衡量整個(gè)數(shù)控加工中心可靠性的重要指標(biāo)之一。對(duì)磨削電主軸的可靠性進(jìn)行試驗(yàn)和評(píng)估，能夠掌握其在實(shí)際使用過(guò)程中實(shí)現(xiàn)預(yù)定功能的能力，同時(shí)可以指導(dǎo)設(shè)計(jì)人員對(duì)其結(jié)構(gòu)和相關(guān)參數(shù)進(jìn)行改善，從而不斷提高磨削電主軸的可靠性。由于電主軸屬于高精度、長(zhǎng)壽命、高可靠性產(chǎn)品，在短時(shí)間內(nèi)對(duì)其進(jìn)行可靠性試驗(yàn)難以獲得失效壽命數(shù)據(jù)。因此，針對(duì)本課題涉及到的這類無(wú)故障情形下的磨削電主軸可靠性評(píng)估的問(wèn)題，擬采用基于Bayes法的可靠性分析法進(jìn)行研究。基于Bayes法的可靠性分析法是一種綜合經(jīng)驗(yàn)信息進(jìn)行可靠性評(píng)估的方法[1]。該方法的特點(diǎn)在于先驗(yàn)分布，根據(jù)先驗(yàn)分布和試驗(yàn)數(shù)據(jù)導(dǎo)出后驗(yàn)分布，繼而得到可靠性指標(biāo)的貝葉斯推斷，因此不需要很多的樣本就能得到較好的估計(jì)。

近些年，國(guó)內(nèi)外學(xué)者在這方面也取得了很多成果，使貝葉斯法得到了不斷的改進(jìn)和完善。如韓明[2]提出了產(chǎn)品無(wú)失效數(shù)據(jù)的一種“綜合新Bayes估計(jì)法”。劉少剛等[3]針對(duì)艦船特種閥門可靠性評(píng)估比較困難的問(wèn)題，提出了將Bayes理論和相似性理論相結(jié)合的評(píng)估新方法。此外，針對(duì)各類研究對(duì)象是小樣本或者極小子樣的情況，也有許多學(xué)者分別提出了不同的方法進(jìn)行研究。如劉騰騰，劉建等[4]采用Bayes法結(jié)合最小二乘法來(lái)分析滾動(dòng)軸承小樣本無(wú)失效數(shù)據(jù)；馮蘊(yùn)雯等[5]研究了在具有相同驗(yàn)前概率值的情況下,不同典型驗(yàn)前概率分布模型對(duì)做一次成功試驗(yàn)后所得的驗(yàn)后概率值的影響；曹浪等[6]研究了小樣本情況下常見(jiàn)驗(yàn)前信息分布、驗(yàn)前信息的獲取方法、驗(yàn)前信息的可信度確定，進(jìn)而將Bayes法運(yùn)用到性能退化模型的建立過(guò)程中。此外，文獻(xiàn)[7-16]也對(duì)Bayes方法進(jìn)行了深入地研究、拓展和應(yīng)用。

此外，由于電主軸造價(jià)較高，使得試驗(yàn)成本較大，因此涉及到的電主軸樣本只有兩根。針對(duì)這類極小子樣的可靠性研究，為了使電主軸可靠性評(píng)估結(jié)果的準(zhǔn)確度更高，擬同時(shí)采用虛擬增廣樣本法將試驗(yàn)樣本的截尾試驗(yàn)壽命進(jìn)行虛擬擴(kuò)展。在此基礎(chǔ)上，對(duì)虛擬增廣樣本進(jìn)行統(tǒng)計(jì)分析，以獲得電主軸的一系列可靠性指標(biāo)。因此，應(yīng)用本方法對(duì)磨削電主軸進(jìn)行可靠性評(píng)估，既縮短了磨削電主軸可靠性試驗(yàn)時(shí)間，又使得最終的評(píng)估結(jié)果不失精確性。

1Bayes法的基本流程

對(duì)于試驗(yàn)樣本的可靠性數(shù)據(jù)所服從的分布函數(shù)中的未知參數(shù)θ，應(yīng)用Bayes法進(jìn)行估計(jì)的基本流程如下：

(1) 根據(jù)未知參數(shù)θ的先驗(yàn)信息確定θ的先驗(yàn)分布π(θ)。

(2) 確定依賴于未知參數(shù)θ的密度函數(shù)p(x|θ)。該函數(shù)表示在隨機(jī)變量θ給定某個(gè)值時(shí)，總體指標(biāo)X的條件分布。根據(jù)貝葉斯觀點(diǎn)，可得密度函數(shù)p(x|θ)為：

(1)

此函數(shù)亦稱為似然函數(shù)，記為L(zhǎng)(θ)。

(3) 由先驗(yàn)分布π(θ)和密度函數(shù)p(x|θ)可得到樣本x和參數(shù)θ的聯(lián)合分布為：

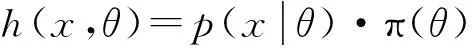
(2)

(4) 推斷未知參數(shù)θ的后驗(yàn)分布。先將h(x,θ)分解為：

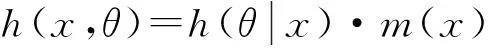
(3)

式中:m(x)是x的邊際密度函數(shù)，其表達(dá)式為：

(4)

由式(4)可知m(x)中不含θ的任何信息，其中Θ是θ的取值空間。因此只能用條件分布h(θ|x)來(lái)對(duì)θ作出統(tǒng)計(jì)推斷，其計(jì)算表達(dá)式為：

(5)

式(5)即為貝葉斯公式的密度函數(shù)形式。

在樣本x給定下，θ的條件分布h(θ|x)被稱為θ的后驗(yàn)分布，其包含了總體、樣本和先驗(yàn)等三種信息中有關(guān)未知參數(shù)θ的所有信息，同時(shí)又排除了所有與θ無(wú)關(guān)的信息[17-19]，所以基于后驗(yàn)分布h(θ|x)對(duì)θ進(jìn)行統(tǒng)計(jì)推斷比基于先驗(yàn)分布的推斷更為有效、更為合理。

2基于Bayes法的電主軸可靠性評(píng)估

2.1理論研究

由于迄今為止對(duì)于磨削電主軸的可靠性試驗(yàn)不夠普遍，開(kāi)展的相關(guān)工作也不是非常的系統(tǒng)，因此人們對(duì)于電主軸的失效所應(yīng)服從的分布也不是很明確。鑒于這種情形，我們致力于在整個(gè)電主軸單元中尋求一些對(duì)于電主軸綜合性能影響較大的典型零部件，并且該部件在工程中的可靠性試驗(yàn)應(yīng)已經(jīng)較為完善和普遍，其失效所服從的分布也應(yīng)較為明確。在此基礎(chǔ)上，可將該典型零部件的失效分布函數(shù)近似代替電主軸的失效分布函數(shù)。

在該思想的指導(dǎo)下，電主軸的支承軸承的磨損及疲勞剝落等形式的失效對(duì)于電主軸的綜合性能(如電主軸的軸端跳動(dòng)和主軸振動(dòng)等)影響較大，也較直接，同時(shí)對(duì)于軸承的研究技術(shù)已發(fā)展得較為成熟，部分企業(yè)和科研院校都對(duì)其開(kāi)展過(guò)長(zhǎng)期的可靠性試驗(yàn)，對(duì)所獲得的大量試驗(yàn)數(shù)據(jù)的分析可獲知其失效所服從的分布為威布爾分布函數(shù)。因此我們最終選擇威布爾分布函數(shù)來(lái)近似代替電主軸的失效分布函數(shù)。

針對(duì)本研究對(duì)象的實(shí)際狀況，推斷威布爾分布的Bayes分析方法：

兩參數(shù)威布爾分布的分布函數(shù)為：

(6)

令：λ=(1/η)m，則式(6)轉(zhuǎn)化為：

F(t)=1-exp(-λtm)

(7)

對(duì)于參數(shù)λ，可選擇伽瑪分布Γ(σ,τ)作為其共軛先驗(yàn)分布；對(duì)于參數(shù)m則沒(méi)有共軛先驗(yàn)分布，由于電主軸屬于高可靠性、長(zhǎng)壽命產(chǎn)品，因此其失效率是遞增的，即m>1,此時(shí)可令m1=m-1,則可取m1的先驗(yàn)分布為伽瑪分布Γ(α,β)。又因?yàn)棣撕蚼1是相互獨(dú)立的，因此可得λ和m1的先驗(yàn)分布為：

(8)

由于涉及到的研究對(duì)象——電主軸屬于高可靠性產(chǎn)品，在短時(shí)間內(nèi)很難得到失效壽命數(shù)據(jù)，因此專門在無(wú)失效壽命數(shù)據(jù)的條件下進(jìn)行研究。在無(wú)失效情形下，相應(yīng)的似然函數(shù)為：

(9)

式中:t1,t2,…,tn指的是對(duì)n個(gè)試驗(yàn)樣品逐個(gè)進(jìn)行定時(shí)截尾試驗(yàn)的截尾試驗(yàn)時(shí)間。

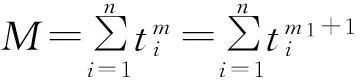
L(λ,m1)=e-λM

(10)

于是可得樣本t1,…,tn和參數(shù)λ、m1的聯(lián)合分布h(t1,…,tn|λ,m1)為：

h(t1,…,tn|λ,m1)=L(λ,m1)·π(λ,m1)=

(11)

將式(11)代入式(5)可得λ和m1的聯(lián)合后驗(yàn)分布h(λ,m1|t1,…,tn)為：

(12)

由式(12)可得到m1的后驗(yàn)分布為：

(13)

而λ的后驗(yàn)分布為：

(14)

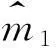
(15)

(16)

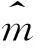
(17)

(18)

2.2磨削電主軸可靠性試驗(yàn)及評(píng)估

2.2.1試驗(yàn)設(shè)備及原理[20]

采用逐次定時(shí)截尾試驗(yàn)的可靠性試驗(yàn)方法，且均在主軸轉(zhuǎn)速為8 000 r/min，軸端徑向載荷為80 N的試驗(yàn)條件下，對(duì)兩根磨削電主軸進(jìn)行可靠性試驗(yàn)，其主要試驗(yàn)設(shè)備見(jiàn)圖1。

1. 振動(dòng)速度傳感器　2. 激光位移傳感器感測(cè)頭 3.離心式風(fēng)機(jī)　4. 恒流源　5.加載盤 6. 電磁加載裝置　7. 磨削電主軸 圖1　電主軸實(shí)驗(yàn)設(shè)備 Fig.1 The electric spindle test equipment

該試驗(yàn)平臺(tái)的主要工作原理是：在接通所有設(shè)備電源之后，先啟動(dòng)水冷機(jī)給電主軸通循環(huán)冷卻水，再通過(guò)調(diào)節(jié)變頻器控制電主軸的轉(zhuǎn)速達(dá)到8 000 r/min，接著啟動(dòng)恒流源給電磁加載裝置供電，以實(shí)現(xiàn)對(duì)電主軸軸端加載盤施加電磁力，并根據(jù)磨削電主軸的載荷譜控制電磁加載力的大小，由此模擬電主軸在實(shí)際磨削加工過(guò)程中的磨削力。然后，在電主軸運(yùn)行穩(wěn)定后，每隔一段時(shí)間通過(guò)激光位移傳感器和振動(dòng)速度傳感器分別測(cè)量電主軸軸端徑向跳動(dòng)量和振動(dòng)速度值，檢查各項(xiàng)指標(biāo)是否超過(guò)允許值。在截尾試驗(yàn)時(shí)間內(nèi)，若各指標(biāo)均未超出允許值，則試驗(yàn)至設(shè)定的截尾時(shí)間時(shí)停止試驗(yàn)；若某指標(biāo)超出允許值，則即刻終止試驗(yàn)。

2.2.2磨削電主軸可靠性評(píng)估

在開(kāi)展整個(gè)試驗(yàn)前，將兩個(gè)試驗(yàn)樣品逐個(gè)進(jìn)行定時(shí)截尾試驗(yàn)的截尾試驗(yàn)時(shí)間分別設(shè)定為955 h、1 452 h，最終各試驗(yàn)樣品在各自的可靠性截尾試驗(yàn)時(shí)間內(nèi)均未出現(xiàn)失效。在此基礎(chǔ)上，首先根據(jù)虛擬增廣樣本法的基本原理，即虛擬增廣后的虛擬樣本的均值應(yīng)與原始試驗(yàn)樣本的均值相等，而且其標(biāo)準(zhǔn)差應(yīng)與類似件的樣本標(biāo)準(zhǔn)差相等[21]，選取虛擬增廣樣本數(shù)為13，即將原始的2個(gè)擴(kuò)展為13個(gè)。根據(jù)威布爾分布密度函數(shù)的偏態(tài)性，可得截尾試驗(yàn)壽命的虛擬增廣樣本為T1=120.35 h，T2=361.05 h，T3=481.40 h，T4=601.75 h，T5=722.10 h，T6=842.45 h，T7=962.80 h，T8=1 083.2h，T9=1 203.5 h，T10=1 444.2 h，T11=1 684.9 h，T12=1 925.6 h，T13=2 482 h。

然后采用“2.1’所闡述的理論對(duì)磨削電主軸的可靠性進(jìn)行評(píng)估，具體過(guò)程如下：

由文獻(xiàn)[22]可知球軸承的形狀參數(shù)一般取為1.5，因此擬取電主軸的疲勞失效壽命所符合的威布爾分布形狀參數(shù)m的初值為1.5。在此基礎(chǔ)上，結(jié)合文獻(xiàn)[1]介紹的先驗(yàn)分布中超參數(shù)的確定方法，確定m1(m1=m-1)的先驗(yàn)分布——伽瑪分布Γ(α,β)和λ的先驗(yàn)分布——伽瑪分布Γ(σ,τ)中的超參數(shù)α，β，σ和τ。

根據(jù)先驗(yàn)信息只能獲得m1的先驗(yàn)均值為：

(19)

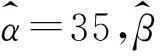
由于本研究的磨削電主軸的應(yīng)用場(chǎng)合是數(shù)控加工中心或者數(shù)控磨床，對(duì)于此類應(yīng)用場(chǎng)合而言，電主軸的主要失效形式是加工精度的喪失，而不是其內(nèi)部材料的疲勞失效。而相對(duì)疲勞失效的壽命而言，加工精度的喪失失效壽命較短，并且很難精確獲得。此外，精度壽命與電主軸的實(shí)際工況和用戶的維護(hù)情況關(guān)系較大。因此，考慮到所研究的磨削電主軸的實(shí)際狀況，結(jié)合蔣喜等[20]的分析結(jié)果，初選電主軸的特征壽命為2 500h，即威布爾分布中的真尺度參數(shù)η=2 500，則參數(shù)λ的先驗(yàn)均值為：

(20)

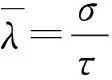
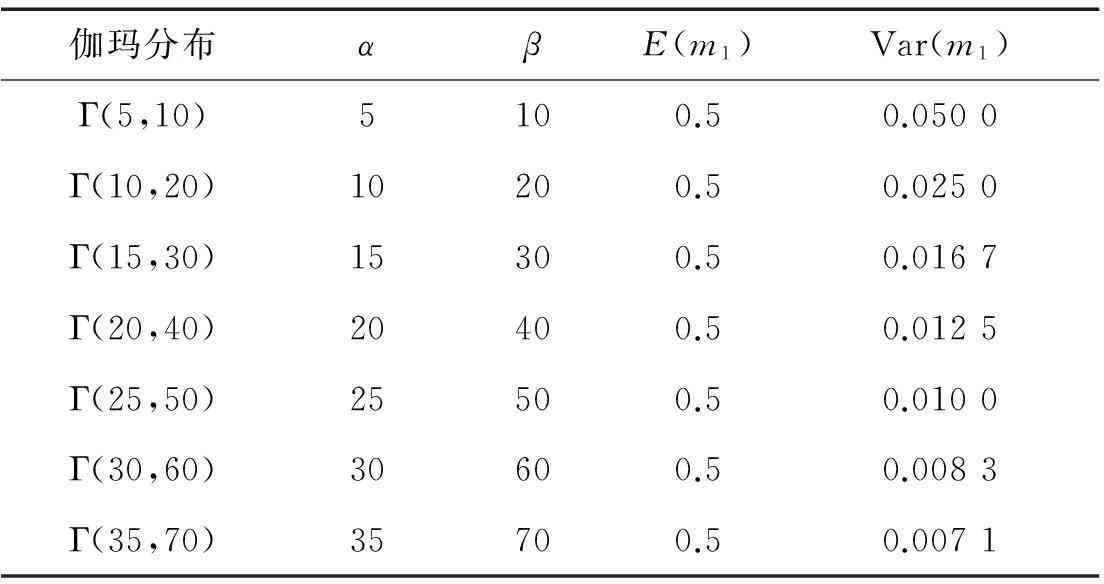
表1　伽瑪分布Γ(α,β)中超參數(shù)與方差的關(guān)系

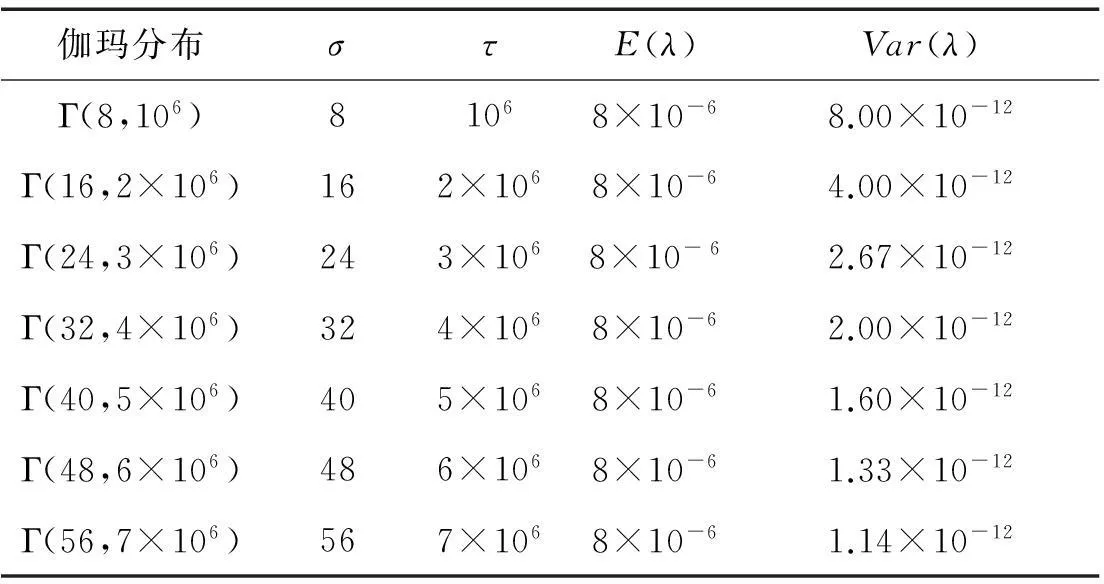
表2　伽瑪分布Γ(σ,τ)中超參數(shù)與方差的關(guān)系

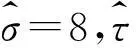
由Bayes法所獲得的磨削電主軸可靠度函數(shù)曲線可知：隨著磨削電主軸使用時(shí)間的延長(zhǎng)，磨削電主軸的可靠度也隨之不斷降低。

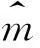
(21)

將上述相關(guān)參數(shù)的貝葉斯估計(jì)值分別代入兩參數(shù)威布爾分布的相關(guān)函數(shù)表達(dá)式，可得磨削電主軸的可靠性指標(biāo)如下：

(1) 平均壽命的估計(jì)值E(T)為：

(22)

(2) 失效分布函數(shù)F(t)和分布密度函數(shù)f(t)分別為:

1-exp(-7.264×10-6×t1.459 4)

(23)

(24)

則由式(24)可得磨削電主軸的失效分布密度函數(shù)曲線，如圖3所示。同時(shí)可得，當(dāng)t≈1 510 h時(shí)，f(t)max=2.230 2×10-4。這表示在本課題設(shè)定的工況下，該型號(hào)電主軸的試驗(yàn)樣本中大約運(yùn)行到1 510h時(shí)失效的個(gè)體總數(shù)占整個(gè)試驗(yàn)樣本的比例是最大的，約為0.022 3%。

(3) 由上述分析易得，電主軸的可靠度函數(shù)為：

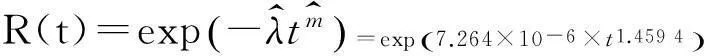
(4) 電主軸失效率函數(shù)為：

(26)

由此可得電主軸失效率函數(shù)曲線如圖4所示。

由圖4可知：磨削電主軸的失效率函數(shù)為遞增型，在運(yùn)行約8 000h的時(shí)候，其失效率達(dá)到6.585 2×10-4(個(gè))/h，該值表示每10 000根該型號(hào)磨削電主軸在本課題設(shè)定的工況下工作8 000h后只有約7根電主軸失效。而在此時(shí)間點(diǎn)之前，各個(gè)時(shí)刻電主軸的失效率均低于6.585 2×10-4(個(gè))/h。由此可見(jiàn)，該電主軸的可靠性較高。

圖2 磨削電主軸可靠度函數(shù)曲線Fig.2Reliabilityfunctioncurveofgrindingmotorizedspindle圖3 磨削電主軸分布密度函數(shù)曲線Fig.3Distributiondensityfunctioncurveofgrindingmotorizedspindle圖4 磨削電主軸失效率函數(shù)曲線Fig.4Failureratefunctioncurveofgrindingmotorizedspindle

(5) 該電主軸的可靠壽命為：

(27)

則其中位壽命為：

(28)

特征壽命為：

(29)

3評(píng)估結(jié)果的比較

采用Bayes法結(jié)合虛擬增廣樣本法對(duì)磨削電主軸極小子樣的可靠性進(jìn)行評(píng)估，將其評(píng)估結(jié)果與蔣喜[20]采用基于偽壽命分布法結(jié)合虛擬增廣樣本法的磨削電主軸極小子樣可靠性評(píng)估方法的評(píng)估結(jié)果進(jìn)行比較，各個(gè)可靠性指標(biāo)的對(duì)比圖表分別見(jiàn)圖5～圖7和表3。

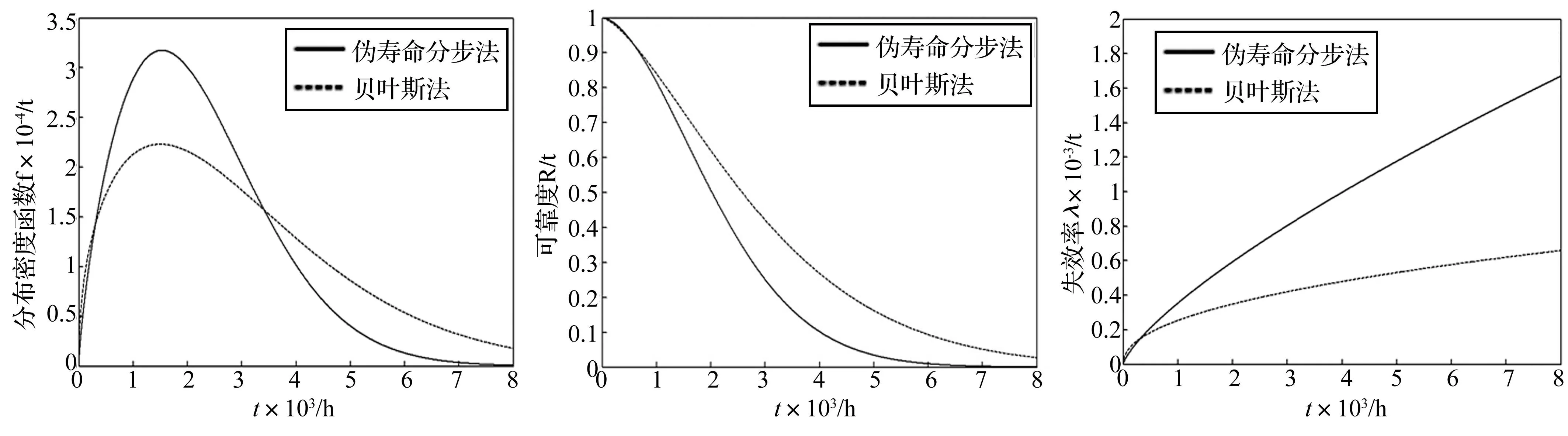
圖5 磨削電主軸的分布密度函數(shù)曲線對(duì)比圖Fig.5Contrastingofdistributiondensityfunctioncurveofgrindingmotorizedspindle圖6 磨削電主軸的可靠度函數(shù)曲線對(duì)比圖Fig.6Contrastingofreliabilityfunctioncurveofgrindingmotorizedspindle圖7 磨削電主軸的失效率函數(shù)曲線對(duì)比圖Fig.7ContrastingofFailureratefunctioncurveofgrindingmotorizedspindle

表3　磨削電主軸部分可靠性指標(biāo)匯總表

由圖5～圖7及表3易知：由兩種不同可靠性評(píng)估方法獲得的關(guān)于磨削電主軸的一系列可靠性指標(biāo)不同，存在一定的差異。造成這種差異主要是因?yàn)橛绊懮鲜鰞煞N方法分析結(jié)果的因素不同，偽壽命分布法的主要影響因素是退化軌跡模型的選取和失效閾值的確定，Bayes法的主要影響因素是先驗(yàn)分布的確定以及先驗(yàn)分布中超參數(shù)的確定。其中失效閾值的確定主要是由電主軸在實(shí)際工況下所需達(dá)到的加工精度等條件決定的，而先驗(yàn)分布是根據(jù)經(jīng)驗(yàn)和歷史資料來(lái)確定的。

對(duì)于本課題的研究對(duì)象而言，由于其可靠性指標(biāo)暫無(wú)統(tǒng)一的標(biāo)準(zhǔn)，因此無(wú)法衡量?jī)煞N可靠性評(píng)估方法的優(yōu)劣。但其中兩者的分布密度函數(shù)、可靠度函數(shù)和失效率函數(shù)的變化趨勢(shì)基本一致，在一定范圍內(nèi)也處于同一數(shù)量級(jí)的水平，并且兩者的平均壽命、中位壽命及特征壽命等指標(biāo)也較為接近，因而在一定程度上體現(xiàn)出兩種可靠性評(píng)估方法對(duì)磨削電主軸的可靠性進(jìn)行評(píng)估均有一定的合理性。

4結(jié)論

針對(duì)采用傳統(tǒng)基于壽命數(shù)據(jù)的可靠性分析方法對(duì)磨削電主軸的可靠性進(jìn)行評(píng)估較為困難的問(wèn)題，提出了將Bayes與虛擬增廣樣本相結(jié)合的可靠性分析方法來(lái)解決磨削電主軸的極小子樣可靠性問(wèn)題，主要研究工作為：

(1) 研究了Bayes法的基本原理和流程，并對(duì)基于Bayes法的磨削電主軸可靠性評(píng)估方法進(jìn)行了理論分析。

(2) 結(jié)合磨削電主軸試驗(yàn)數(shù)據(jù)，應(yīng)用基于Bayes法的磨削電主軸可靠性分析方法對(duì)磨削電主軸進(jìn)行可靠性評(píng)估，獲得一系列可靠性指標(biāo)。

(3) 將基于Bayes法的磨削電主軸極小子樣可靠性評(píng)估結(jié)果與基于偽壽命分布法的磨削電主軸極小子樣可靠性評(píng)估結(jié)果進(jìn)行比較，以驗(yàn)證本文研究的合理性。

評(píng)估結(jié)果表明，該電主軸的可靠度隨時(shí)間的變化趨勢(shì)基本符合機(jī)械產(chǎn)品的性能退化規(guī)律，同時(shí)其平均失效壽命基本符合正常工況下的一般范圍。

參 考 文 獻(xiàn)

[1] 趙宇.可靠性數(shù)據(jù)分析[M].北京：國(guó)防工業(yè)出版社，2011.

[2] 韓明.產(chǎn)品無(wú)失效數(shù)據(jù)的綜合處理[J].機(jī)械工程學(xué)報(bào)，2003,39(2):129-132.

HAN Ming. Synthesized process for zero-failure data of the products[J].Journal of Mechanical Engineering，2003,39(2):129-132.

[3] 劉少剛，李少杰，舒海生，等.小子樣狀態(tài)下艦船特種閥門可靠性評(píng)估方法研究[J].哈爾濱工程大學(xué)學(xué)報(bào), 2012,33(4):1-5.

LIU Shao-gang，LI Shao-jie，SHU Hai-sheng,et al. Research on reliability assessment of vessel special valve in small sample condition[J].Journal of Harbin Engineering University, 2012,33(4):1-5.

[4] 劉騰騰,劉建亭,崔鳳奎,等.滾動(dòng)軸承小樣本無(wú)失效數(shù)據(jù)的Bayes可靠性分析[J].河南科技大學(xué)學(xué)報(bào),2009,30(6):20-22.

LIU Teng-teng，LIU Jian-ting，CUI Feng-Kui,et al. Reliability analysis about small sample zero failure data of rolling bearing[J].Journal of Henan University of Science and Technology,2009,30(6):20-22.

[5] 馮蘊(yùn)雯,馮元生.極小子樣高可靠性成敗型產(chǎn)品試驗(yàn)的貝葉斯評(píng)估方法研究[J].機(jī)械科學(xué)與技術(shù),1999,18(2): 198-200.

FENG Yun-weng, FENG Yuan-sheng. Study of Bayes’ estimation for product test of extreme small-sample high-reliability safe-or-failure pattern[J].Mechanical Science and Technology,1999,18(2): 198-200.

[6] 曹浪,李銀軍,李獻(xiàn)鋒,等. 基于小樣本Bayes理論的可靠性評(píng)估方法[J].電子質(zhì)量,2010(10):25-27.

CAO Lang，LI Yin-jun，LI Xian-feng,et al. Research on reliability evaluation method based on Bayes theory of small-sample[J].Electronic Quality,2010(10):25-27.

[7] 張曉冉,胡文杰,夏茂輝.分組定時(shí)截尾無(wú)失效數(shù)據(jù)的迭代Bayes分析[J].工程數(shù)學(xué)學(xué)報(bào),2009,26(2): 267-272.

ZHANG Xiao-ran, HU Wen-jie, XIA Mao-hui. Iterative bayes analysis of the grouped, timing terminated and zero-failure data[J].Chinese Journal of Engineering Mathematics,2009,26(2): 267-272.

[8] Wu H C. Bayesian system reliability assessment under fuzzy environments[J].Reliability Engineering & System Safety,2004,83(3):277-286.

[9] Sarhan A. Non-parametric empirical Bayes procedure[J].Reliability Engineering & System Safety, 2003,80(2):115-122.

[10] Taheri S M，Zarei R. Bayesian system reliability assessment under the vague environment[J].Applied Soft Computing,2011,11(2):1614-1622.

[11] 劉永峰,鄭海鷹.無(wú)失效數(shù)據(jù)的統(tǒng)計(jì)分析[J].浙江大學(xué)學(xué)報(bào):理學(xué)版,2012,39(3):273-277.

LIU Yong-feng，ZHENG Hai-ying. Statistical analysis about zero-failure data[J].Journal of Zhejiang University：Science Edition,2012,39(3):273-277.

[12] 韓芳,鐘冬望,汪君.基于貝葉斯法的復(fù)雜有限元模型修正研究[J].振動(dòng)與沖擊,2012,31(1):39-43.

HAN Fang，ZHONG Dong-wang，WANG Jun. Complicated finite element model updating based on Bayesian method [J]. Journal of Vibration and Shock, 2012,31(1):39-43.

[13] 郝騰飛,陳果.基于貝葉斯最優(yōu)核判別分析的機(jī)械故障診斷[J].振動(dòng)與沖擊,2012,31(13):26-30.

HAO Teng-fei，CHEN Guo. Machinery fault diagnosis based on Bayes optimal kernel discriminant analysis[J].Journal of Vibration and Shock,2012,31(13): 26-30.

[14] 邱金水,李少杰,劉少剛,等.艦船特種閥門極少失效條件下可靠性壽命研究[J].哈爾濱工程大學(xué)學(xué)報(bào),2012,33(9):1086-1090.

QIU Jin-shui，LI Shao-jie，LIU Shao-gang,et al. Research on the reliability life of a vessel special valve based on few-failure data[J].Journal of Harbin Engineering University,2012,33(9):1086-1090.

[15] 張建軍,謝敬芝,劉征宇. 基于置信分布和K-L信息距離的成敗型產(chǎn)品可靠性分析[J].電子測(cè)量與儀器學(xué)報(bào),2011,25(4):320-324.

ZHANG Jian-jun，XIE Jing-zhi，LIU Zheng-yu. Bayesian analysis for reliability of success-failure products based on confidence distribution and K-L information distance[J].Journal of Electronic Measurement and Instrument, 2011,25(4):320-324.

[16] 陳振珩,劉雨時(shí). 基于 Bayes 可靠性評(píng)估驗(yàn)前信息檢驗(yàn)方法的研究[J].電子測(cè)量與儀器學(xué)報(bào),2008(S1):41-44.

CHEN Zhen-heng，LIU Yu-shi. Test method of prior information based on bayes reliability evaluation[J].Journal of Electronic Measurement and Instrument,2008(S1):41-44.

[17] 馬彥輝.基于GLM的非正態(tài)響應(yīng)穩(wěn)健設(shè)計(jì)研究[D].天津：天津大學(xué),2008.

[18] 孟利鋒.隨機(jī)波動(dòng)模型及其建模方法研究[D].天津：天津大學(xué),2004.

[19] 任楓.非對(duì)稱雙指數(shù)跳躍擴(kuò)散模型的貝葉斯分析[D].天津：天津大學(xué),2007.

[20] 蔣喜,劉宏昭,劉麗蘭,等.基于偽壽命分布的電主軸極小子樣可靠性研究[J].振動(dòng)與沖擊,2013,32(19):80-85.

JIANG Xi，LIU Hong-zhao，LIU Li-lan，et al. Research on extremely small-scale sample’s reliability of electric spindle based on distribution of false life[J].Journal of Vibration and Shock,2013,32(19):80-85.

[21] 黃瑋，馮蘊(yùn)雯，呂震宙.極小子樣實(shí)驗(yàn)的虛擬增廣樣本評(píng)估方法[J].西北工業(yè)大學(xué)學(xué)報(bào)，2005，23( 3)： 384-387．

HUANG Wei，F(xiàn)ENG Yun-wen，Lü Zhen-zhou. Virtually expanded sample estimation method for extremely small-scale sample test[J].Journal of Northwestern Polytechnical University，2005，23(3)： 384-387．

[22] 楊曉蔚. 滾動(dòng)軸承疲勞壽命威布爾分布三參數(shù)的研究[D].合肥：合肥工業(yè)大學(xué),2003.