基于改進最小噪聲分離變換的異常檢測算法

王　坤，屈惠明

(南京理工大學 電子工程與光電技術學院，南京 210094)

文章編號：1001-3806(2015)03-0381-05

基于改進最小噪聲分離變換的異常檢測算法

王坤，屈惠明*

(南京理工大學 電子工程與光電技術學院，南京 210094)

摘要：為了降低噪聲對高光譜異常檢測結果的影響以及提高異常檢測率，提出了一種基于改進最小噪聲分離(MNF)變換的新型高光譜異常檢測算法。首先對傳統的MNF變換進行改進，采用加權鄰域均值法對噪聲矩陣進行估計，對鄰域內每一個像元給予一個特定的權值，提高背景像元在鄰域矩陣中的比例，進而抑制噪聲像元的比例，通過差值計算提取噪聲信息，然后應用改進的MNF變換對高光譜圖像進行降維去噪處理，最后，將獲取的低維去噪圖像利用異常檢測算法進行檢測，并用真實的AVIRIS數據進行了測試。結果表明，該算法有更好的降維去噪效果，提高了異常檢測率。

關鍵詞：光譜學；最小噪聲分離；加權鄰域均值法；異常檢測

中圖分類號：TP751.1

文獻標志碼：A

doi:10.7510/jgjs.issn.1001-3806.2015.03.022

Anomaly detection method based on improved

minimum noise fraction transformation

WANGKun,QUHuiming

(School of Electronic and Optical Engineering, Nanjing University of Science & Technology， Nanjing 210094, China)

Abstract：In order to reduce the influence of noise on the detection results of hyperspectral anomaly detection and improve the rate of anomaly detection，a new anomaly detection process based on improved minimum noise fraction (MNF) transformation was proposed. Firstly, to improve the traditional MNF transform, the weighted neighborhood averaging method was used to estimate the noise matrix,a specific weight was given to each pixel of the neighbor matrix for increasing the portion of background pixels and suppressing the noise pixels in the sample matrix. It was an effective way to extract noise information by calculating the difference. Secondly, improved MNF transform was used to reduce the dimension of hyperspectral image data and to separate the noise from signals effectively．Finally, anomaly detection algorithm was implemented on low-dimensional denoised data. After actual test of AVIRIS data, the results show that the improved algorithm has better effect of reducing the dimension and separating the noise, and the rate of anomaly detection is improved significantly.

Key words:spectroscopy; minimum noise fraction; weighted neighborhood averaging method; anomaly detection

*通訊聯系人。E-mail：huimingqu@163.com

引言

在現代遙感技術體系中，高光譜遙感自20世紀80年代異軍突起。雖然它是個后來者，但經過近30年的迅猛發展，已充分表現出在信息獲取方面的巨大優勢和潛力，同時也逐步顯露其在數據分析處理及地物與目標精細探測等方面獨有的技術特色和魅力[1]。因此，利用高光譜圖像對目標進行檢測與識別[2]在國內外引起廣泛關注。實際應用中，地物的種類是豐富多彩的。受環境的影響及測量條件的變化，完備而又實用的地物光譜數據庫很難獲得。此外，精準的反射率反演算法還有待發展和完善，這都導致了有先驗信息的目標檢測在實際應用中變得更加困難[3]。因此,對于不需要先驗光譜信息的異常目標檢測的研究具有非常重要的意義[4]。

通常的異常檢測算法基本都是基于概率統計模型的，主要有RX異常檢測算法[5]、低概率目標檢測算法[6]和均衡目標探測算法[7]等。其中，由REED和YU發展起來的RX算法[5]是比較經典的異常檢測算法之一。由于RX算法只考慮到數據的2階統計特性，忽略了數據的非線性特性，這在一定程度上限制了算法的性能，于是KWON等人提出了基于核的非線性RX( KRX)算法[8]，利用一個核函數將原始高光譜數據映射到高維特征空間，相比于RX算法大大地提高了檢測性能。

不管RX算法還是KRX算法，都是對原始高光譜數據直接進行檢測。由于原始高光譜數據存在數據量大，并且包含大量冗余信息及噪聲，這在一定程度上限制了算法的檢測性能。因此，作者提出了基于改進最小噪聲分離(minimum noise fraction，MNF)[9]變換的異常檢測算法。首先對高光譜數據使用改進最小噪聲分離(improved MNF,IMNF)變換進行降維去噪處理，然后進行異常檢測。經實驗驗證，該方法取得了較好的檢測效果。

1MNF變換及改進

考慮了噪聲和區域對影像的影響，并且以信噪比為度量的最小噪聲分離變換可以對高光譜影像進行成分分解和排列。該方法具有完備的理論支撐，是一種比較有效的降維去噪方法。

為了實現MNF變換，最重要的一步就是對噪聲進行準確估計以獲得噪聲協方差矩陣。以下是MNF變換的具體實施步驟。

(1)把混有噪聲的信號進行高通濾波處理，得到噪聲協方差矩陣Σn。

(2)計算噪聲協方差矩陣Σn的特征值λ和特征向量P，由λ組成的對角矩陣記為Δ，由P組成的矩陣記為E。

(3)求Σn的白化矩陣F：

(4)計算噪聲白化之后的觀測數據FTZ的協方差矩陣:

式中，Z為影像數據，Σz為影像的協方差矩陣。

(5)由Σw求得特征值和特征向量，由所有特征值構成的對角矩陣記為Λ，相應特征向量構成的矩陣記為G。

(6)將G作用到FTZ的每個像元上，GTFTZ即為MNF變換后得到的圖像。

變換后獲得的向量中的各元素相互獨立，其中第一分量中聚集了大量的信息，影像質量隨著維數的增加而逐漸下降，以信噪比從大到小的順序進行排列，不同于主成分分析法，從而克服了噪聲對影像質量的影響[10]。

傳統的MNF變換中，通常采用像元與相鄰像元的差值對影像數據噪聲進行估計。但是，圖像中噪聲是隨機的，既可能為椒鹽噪聲也可能為條帶噪聲，或者二者都有。條帶噪聲可能是水平條帶，也可能是縱向條帶。這種情況下采用像元與相鄰像元的差值來對噪聲進行估計就會受到很大的影響。為了彌補該算法的局限性，作者提出了加權鄰域均值法對噪聲矩陣進行估計，對目標像元鄰域內8個像元賦予一定的權值，如圖1所示，增強背景像素在鄰域矩陣中的比例，壓制噪聲像素的比例。通過計算目標像元與鄰域均值之間的差值來提取噪聲信息。

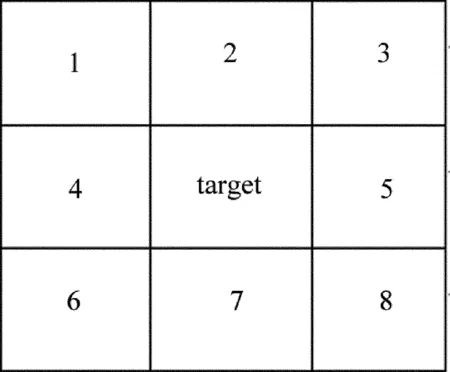
Fig.1　Example of detection window

本文中采用的權值為各個像素到均值像素的距離倒數，可以寫為：

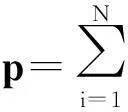
鄰域均值為：

由此可得每一像元處的差值為：

最后通過dX來對噪聲進行評估。

2高光譜異常檢測算法

異常檢測將不同于背景光譜的像素點判定為目標，此過程不需要待檢測目標的先驗光譜特征。由REED和YU(1990年)發展起來的RX算法是比較經典的異常檢測算法。KWON等人在RX算法的基礎上提出了基于核的RX算法(KRX)，通過一個核函數將原始高光譜數據映射到高維特征空間，提高了異常檢測率。本節中主要對這兩種算法進行簡要介紹。

2.1　RX算法

假設目標點的光譜向量為r，背景的均值向量為μ，背景的協方差矩陣為C，則RX算法表達式可寫為：

該算法主要通過計算δRX的值來尋找異常目標。圖像中的異常目標一般與協方差矩陣C的小特征值相對應，從(6)式中可以看出，特征值越小，則δRX越大，將δRX大于某個固定閾值η的認定為異常目標。

2.2　KRX算法

KWON等人將RX算法應用于高維特征空間，構造了基于核空間投影的RX異常檢測算法(KRX)，對應于特征空間的RX算法為：

式中,Φ(r)為原始高光譜數據r通過非線性函數Φ映射到高維特征空間所得，CΦ和μΦ分別為特征空間中從背景樣本估計出的協方差矩陣和均值向量。

由于特征空間是高維的，上式不能直接實現，采用核函數化的RX算法為：

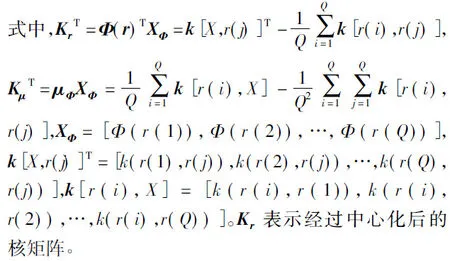
式中,IQ是Q×Q的方陣，所有元素都為1/Q。

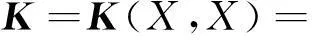
2.3　異常檢測算法流程

鑒于原始高光譜數據存在數據量大，并且包含大量冗余信息及噪聲等特點，在對數據進行異常檢測前作者首先對數據進行降維去噪處理，跟未進行降維處理相比，大大提高了算法的運行速率和效率。具體流程如圖2所示。

Fig.2　Algorithm process

3實驗結果及其分析

3.1　數據描述

為了說明該算法的有效性，實驗中采用AVIRIS數據進行驗證，該數據采集地點為美國圣地亞哥某機場的上空，其波長范圍為0.4μm～2.5μm，總共224個波段，覆蓋了從可見光到近紅外的光譜范圍。將水吸收和噪聲污染厲害的波段去除，選取其中的150個波段進行研究。圖像大小截取為100×100，其中含有38個待檢測目標。圖像的第4個波段和地面真實的目標分布如圖3所示。

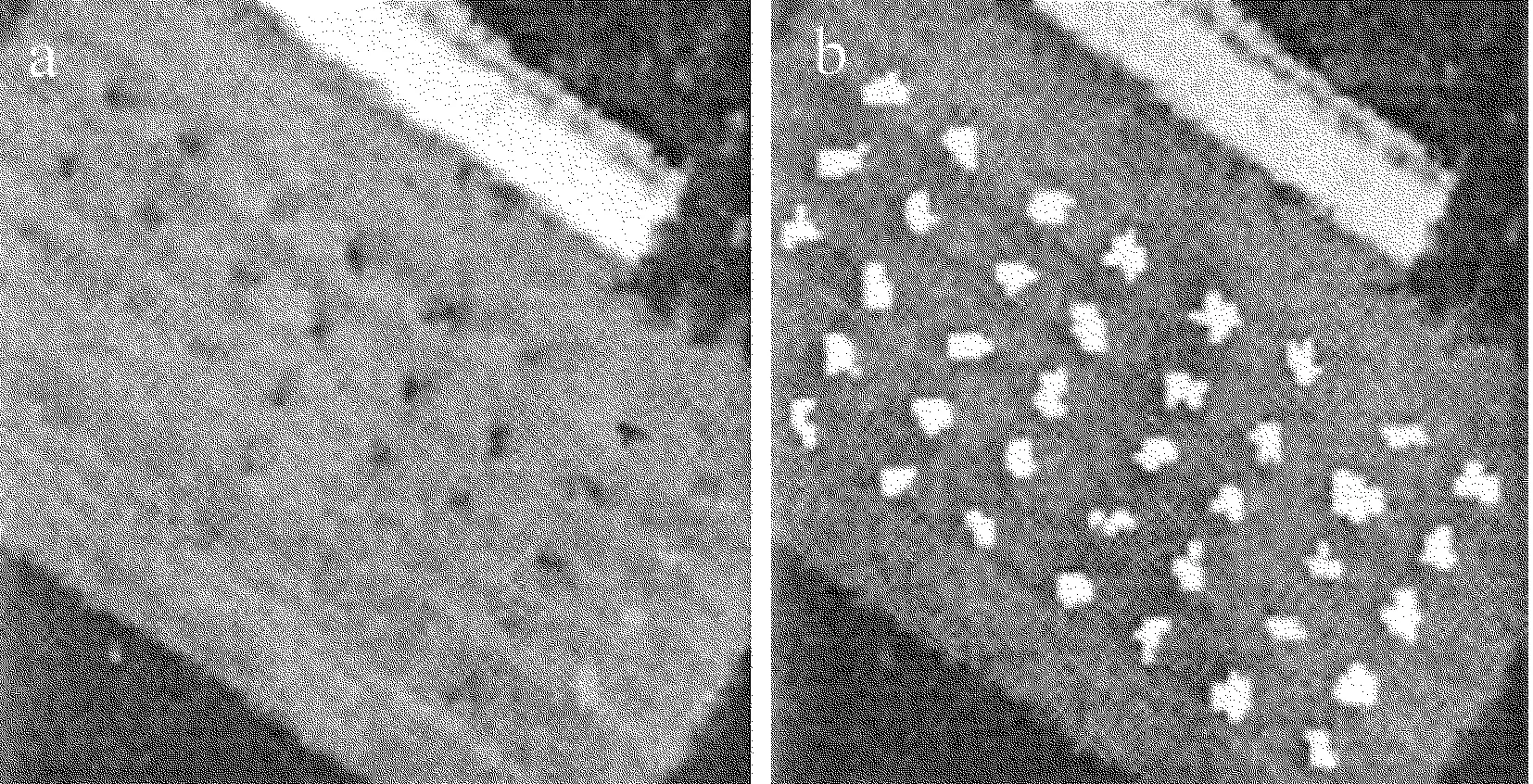
Fig.3Hyperspectral image of AVIRIS and actual distribution of the corresponding target

a—the 4th band of hyperspectral imageb—the distribution of the actual ground target

3.2　實驗結果與分析

首先對原始高光譜數據進行MNF變換，經過變換后得到以信噪比從大到小順序排列的各成分。圖4中顯示了各成分的特征值。

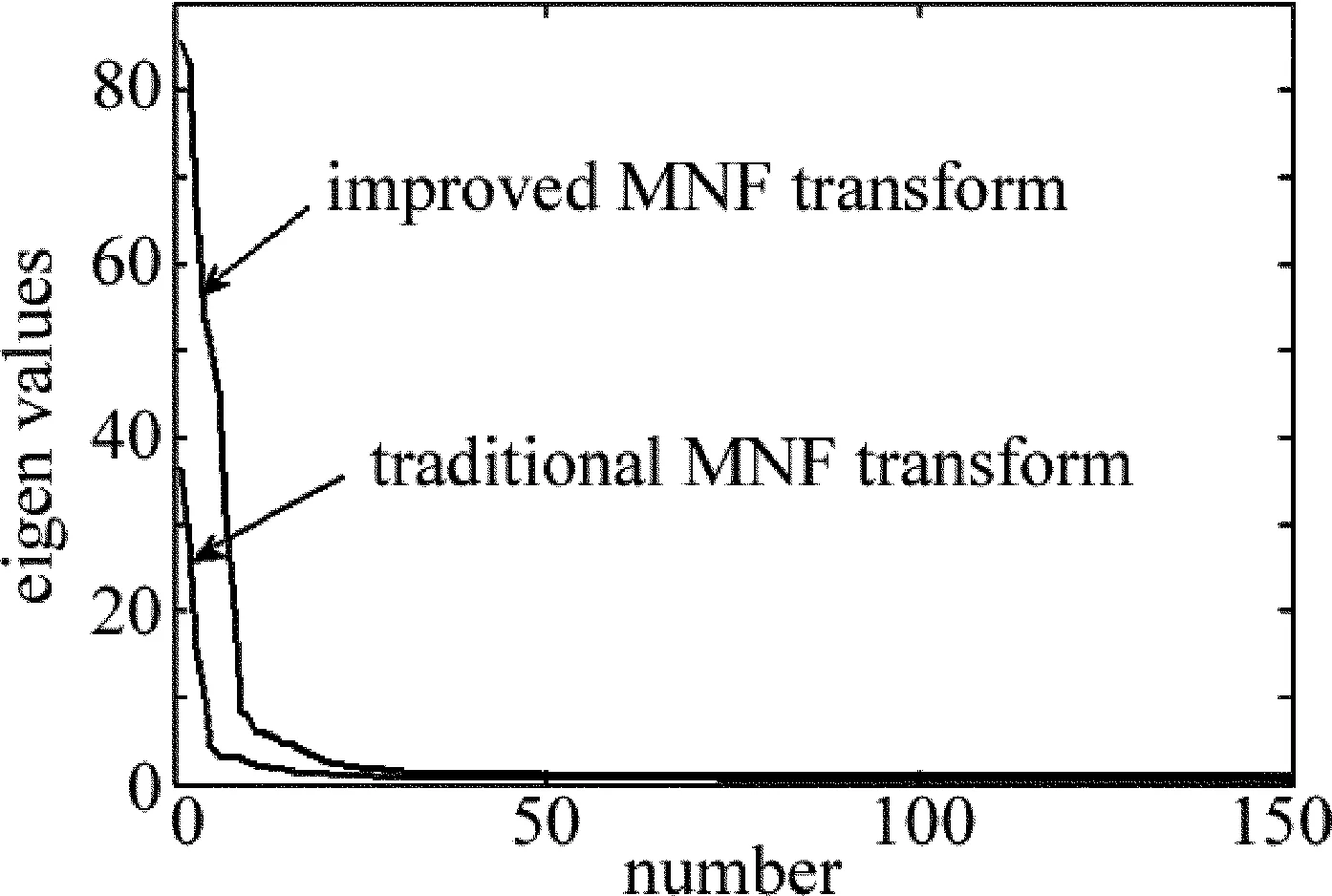
Fig.4Eigenvalue curve of the improved MNF transform and the traditional MNF transform

從圖中可以看出，較低編號的特征值和較高編號的特征值的比值在兩種變化中完全不同。經過改進的MNF變換比值明顯高于傳統MNF變換，這說明改進的MNF變換能夠更加有效地提取不同地物的光譜特征。變換后獲得的向量中的各元素相互獨立，其中第一分量中聚集了大量的信息，影像質量隨著維數的增加而逐漸下降，信噪比也隨之降低，通過信噪比跟每一分量的影像質量綜合考慮來確定選取的波段數目，本文中選取前10個成分組成變換后的低維影像。

綜合考慮圖像的空間大小以及地面分辨率后，在進行RX算法跟KRX算法時,背景窗口設為15像素×15像素，目標窗口設為5像素×5像素。另外，在KRX算法中，采用的核函數為高斯徑向基核函數，函數中的參量只有一個，其表達式為：

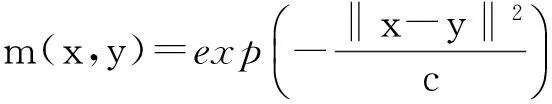
(11)

經過多次試驗，系數c取值為40時具有最理想的檢測效果。

對檢測效果進行灰度閾值分割，該方法是最經典的圖像分割方法[11]。本文中閾值的獲取是通過不斷試驗得到的，目的在于保證具有較少虛警數目的前提下能夠顯示出更多的目標。在試驗過程中首先對數值進行粗糙的分割，選取效果最好的兩幅圖，然后再對所選的兩幅圖所對應的閾值之間進行更細的分割，直到選取出最佳閾值。

為了使檢測結果有更好的可比性，作者使用IMNF-KRX的最佳閾值對不同的檢測結果進行分割，分割獲得的圖像如圖5所示。

Fig.5　Threshold segmentation figure of different algorithms

從圖5的檢測結果比較可以看出，本文中所改進的MNF算法應用于RX算法(IMNFRX)及KRX算法(IMNFKRX)獲得的檢測性能優于未進行降維的RX算法、KRX算法及使用傳統MNF算法進行降維的RX算法(MNF-RX)、KRX算法(MNFKRX)。這是由于直接將RX算法、KRX算法用于原始的高光譜數據時忽略了波段間的相關性，產生了較多的虛警。使用傳統的MNF算法進行降維未考慮到噪聲的復雜性，僅僅采用像元與相鄰像元的差值來對噪聲進行估計就會使算法的性能受到影響，而本文中的方法有效地避免了該種問題的發生。

為了更形象地展示檢測結果，通過3維效果圖(見圖6)來對檢測結果進行展示。

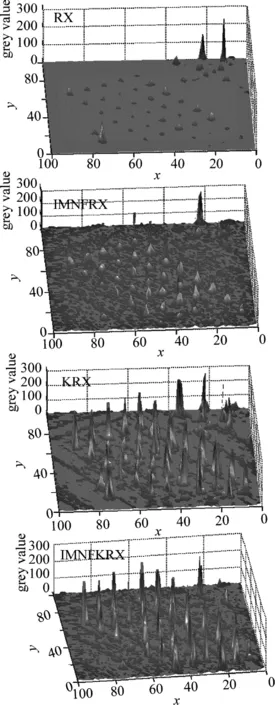
Fig.6　3-D renderings of different algorithms

通過3維圖可以看出，在進行RX及KRX檢測前經過改進MNF變換算法降維可以取得較好的檢測效果。經過降維之后的檢測目標更突出，虛警更少。

另外，接收機工作特性(receiveroperatingcharac-teristic,ROC)曲線可以用于呈現虛警概率Ρf與檢測概率Ρd之間的關系，可以對算法的檢測性能提供定量分析。從圖7中可以看出，在進行RX算法及KRX算法前使用本文中改進的降維算法,能夠獲得較好的檢測性能以及較低的虛警率。

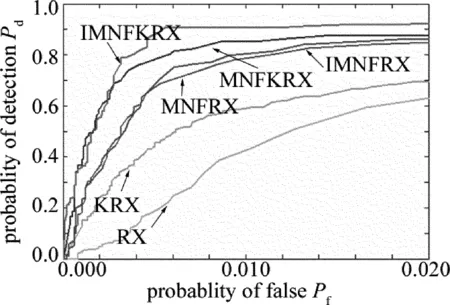
Fig.7　ROC curve of different algorithms

4結束語

提出了基于改進MNF變換的新型異常檢測方法，采用加權方法對MNF變換中樣本噪聲協方差矩陣估計進行改進，對鄰域內每一個像元給予一個特定的權值，提高背景像元在鄰域矩陣中的比例，進而抑制噪聲像元的比例，通過差值計算提取噪聲信息。用真實的AVRIS數據進行實驗測試，結果表明：該方法對高光譜圖像進行降維去噪是有效的，克服了原始數據存在冗余信息及包含噪聲的缺點，提高了異常檢測率。

參考文獻

[1]PURL,GONGP.Hyperspectralremotesensingandapplication[M].Beijing:HigherEducationPress, 2000:22-26 (inChinese).

[2]MEIF,ZHAOChH.Anovelspectralsimilaritymeasurementkernelbasedanomalydetectionmethodinhyperspectralimagery[J].ActaPhotonicaSinica, 2009,38(12):3165-3170(inChinese).

[3]ZHANGLY,YAOP.Hyperspectralimagelowprobabilityanomalydetectionmethodresearchbasedonvertexcomponentanalysis[J].JournalofAstronautics, 2007, 5(9):1262-1265(inChinese).

[4]XIAOXB.Researchofanomalydetectionalgorithmsofhyperspectralimagery[D].Hangzhou:ZhejiangUniversity, 2012:2-7(inChin-ese).

[5]REEDIS,YUXL.Adaptivemultiple-bandCFARdetectionofanopticalpatternwith.unknownspectraldistribution[J]．IEEETransactionsonAcoustics，SpeechandSignalProcessing,1990,38(10):1760-1770.

[6]CHANGCI.Hyperspectralimaging:techniquesforspectraldetectionandclassification[M].NewYork,USA:KluwerAcademic,2003:256-268.

[7]CHANGCI,CHIANGSS.Anomalydetectionandclassificationforhyperspectralimagery[J].IEEETransactionsonGeoscience&RemoteSensing,2002,40(6):1314-1325.

[8]KWONH,NASRABADINM.Kernelspectralmatchedfilterforhyperspectralimagery[J].InternationalJournalofComputerVision,2007,71(2):127-141.

[9]GREENAA,BERMANM,SWITZERP, et al.Atransformationfororderingmultispectraldatainterms.ofimagequalitywithimplicationsfornoiseremoval[J].IEEETransactionsonGeoscienceandRemoteSensing,1988,26(1):65-74．

[10]GUHY,LIHT,YANGJH.Theremotesensingimagefusionmethodbasedonminimumnoisefraction[J].RemoteSensingForLand&Resources, 2007, 13(2):53-56(inChinese).

[11]WEIXF,LIUX.Researchofimagesegmentationbasedon2-Dmaximumentropyoptimalthreshold[J].LaserTechnology, 2013, 37(4):519-522(inChinese).

收稿日期：2014-04-18；收到修改稿日期：2014-07-29

作者簡介：王坤(1989-)，男，碩士研究生，從事高光譜異常檢測及其在隱身評估方面的研究。

基金項目：“十二五”裝備預研資助項目(62201050103);國家自然科學基金資助項目(61171164)