RBF網絡在無刷直流電機控制系統的應用*

李書舟，鄧小龍

(1湖南電氣職業技術學院汽車工程系，湖南湘潭 411000；

2中國電器科學研究院，廣東廣州510300)

?

RBF網絡在無刷直流電機控制系統的應用*

李書舟1，鄧小龍2

(1湖南電氣職業技術學院汽車工程系，湖南湘潭 411000；

2中國電器科學研究院，廣東廣州510300)

摘要研究了無刷電機的控制問題，針對常規PID控制的無刷直流電機系統存在參數難以整定、超調量大、調節時間長、抗干擾能力差等問題，建立了無刷直流電機的數學模型，提出了RBF神經網絡控制在系統中的總體設計方法，并在常規PID控制器的基礎上建立了RBF網絡控制器；利用Matlab軟件對常規PID控制和RBF網絡控制進行仿真比較，結果表明基于RBF網絡控制器能動態調整控制器參數，有效的提高了系統的性能以及控制效果，系統對參數擾動具有較強的魯棒性。

關鍵詞無刷直流電機；RBF神經網絡；Matlab；PID控制器

0引言

二十世紀八十年代，鮑威爾首次提出了基于多變量函數插值的徑向基函數(Radical Basis Function RBF)方法，此后RBF神經網絡的研究得到了中外學者的廣泛關注[1]。RBF神經網絡和其他前向神經網絡一樣，有相似的三層前饋神經網絡結構，模擬人腦中局部調整、相互覆蓋和接收的神經網絡結構，具有運算能力強、速度快以及局部函數逼近的特點，所以它在智能控制、信息處理等領域的應用有著廣闊的前景[2]。

傳統控制理論在無刷直流電機系統的控制中，主要以狀態方程、微分方程及各種變換的方法進行研究，計算本質上仍是數值方法。譬如經典PID控制方法在高頻擾動時，電機速度抖動頻繁，缺乏對干擾變化的應變能力，而常規自適應方法參數調整難，實現成本高，難以確保有好的控制效果[3]。文獻[4]針對橫向永磁電機的調速特點提出了一種RBF神經網絡整定PID參數的控制方法，實時整定修正PID系統控制參數，但對系統抗干擾性能未做分析；文獻[5]提出了一種RBF神經網絡的無刷直流電機調速控制新策略，具有較好的速度響應與超調性，但未給出參數自適應整定曲線。

本文將研究RBF神經網絡整定PID控制無刷直流電機系統上的應用。在此基礎上，研究了其在無刷直流電機系統中的控制效果。建立了無刷直流電機的數學模型，利用神經網絡的非線性適應能力來優化無刷直流電機的PID控制參數，實現對無刷直流電機的有效控制。最后，在控制系統中廣泛存在的階躍響應進行了仿真實驗，得出了系統階躍曲線。結果表明，利用RBF神經網絡控制，系統具有更好的魯棒性[6]。

1無刷直流電機數學模型

無刷直流電機由電機本體、轉子位置傳感器和電子換相線路三大部分組成。定子上導磁的定子鐵心及導電的電樞繞組設計時要求結構簡單，運行可靠，并能產生足夠的磁動勢以得到足夠的轉矩，轉子采用瓦形磁鋼，進行特殊的磁路設計，可獲得梯形波的氣隙磁場，電子換相電路同時能按照位置傳感器的信號進行正確換向和控制，能夠實現電機的正反轉，并且能滿足不同環境條件和長期運行的要求。

以兩相導通星形三相六狀態為例，分析BLDC的數學模型及電磁轉矩等特性。為了便于分析，假定電機定子三相完全對稱，空間上互差120°；三相繞組電阻、電感參數完全相同；轉子永磁體產生的氣隙磁場為方波，三相繞組反電動勢為梯形波；忽略定子繞組電樞反應的影響；電機氣隙磁導均勻，磁路不飽和，不計渦流損耗；電樞繞組間互感忽略。可得到無刷直流電機的數學模型如式(1)所示[7]。

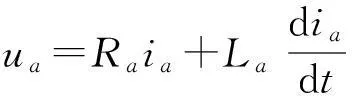
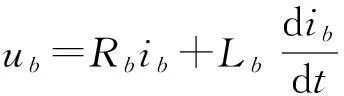
(1)

式中，ua,ub,uc,un—三相端電壓和中點電壓(V);ea,eb,ec—三相電子反電動勢(V)；ia,ib,ic—三相電子相電流(A)；La,Lb,Lc—三相電子自感(H)；Ra,Rb,Rc—三相電子繞組的相電阻(Ω)。

由電機的結構決定，在360°電角度內，轉子的磁阻不隨轉子位置的變化而變化，并假定三相繞組對稱，則有La,Lb,Lc相等，Ra,Rb,Rc相等。

由于三相對稱的電機中，ia+ib+ic=0，以及Mib+Mic=-Mia,un=0，則式(1)可改寫為狀態方程

(2)

式中，P—微分算子。

在電機運行過程中，電磁轉矩的表達式為

Te=(eaia+ebib+ecic)/ω

(3)

式中，ω—轉子角速度(rad/s)。

電機的機械運動方程為

(4)

式中，f—阻尼系數( N·m·s/rad)；J—電機轉動慣量(k g·m2)；TL—負載轉矩( N·m)。

反電動勢系數ke由以下公式計算

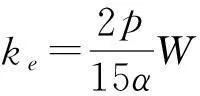
(5)

式中，W—電樞繞組每相串聯的匝數；φ—每極磁通(Wb)。

電機運行過程中瞬態功耗的公式為

(6)

式中，Ω—電機角速度；P—功耗。

2RBF神經網絡控制算法

2.1　常規PID控制算法

PID控制器是由三種運算集合而成，它包括比例調節(P)、積分調節(I)、微分(D)調節。系統誤差經過三種運算調節后，將得到的計算結果作為控制量，反饋回系統形成閉環控制。其形式見式(7)。

(7)

式中，e(t)—采樣輸出與基準信號相減后的偏差信號；kp、ki、kd—比例系數、積分系數和微分系數。運算得到的u(t)作為系統輸入，反饋回系統中。

同樣，在數字控制系統中，使用比較普遍的也是PID控制規律。在傳統的PID控制中，存在比例、積分、微分這三種控制作用。比例控制的優點是:誤差一旦產生，控制器立即就有控制作用，使被控制量朝著誤差減小的方向變化，其控制作用的強弱取決于比例系數kp。比例控制的缺點是對于系統階躍響應值為一有限值的被控對象存在靜差。加大其值可以減小靜差，但kp過大時，會破壞系統的動態性能，甚至使閉環系統不穩定。

積分控制的優點是：它能對誤差進行記憶并積分，有利于消除靜差。積分控制的缺點在于積分作用具有滯后特性。如果積分控制作用太強就會使系統的動態性能變差，甚至使系統變得不穩定。

微分控制的優點是：它能對誤差進行微分，敏感于誤差的變化趨勢，增大微分控制可以加快系統響應，使超調量減小，增加系統穩定性。它的缺點是對于干擾同樣敏感，使系統抑制干擾能力降低。

2.2　RBF神經網絡模型

RBF神經網絡模型由鮑威爾于1985年提出，它是神經網絡中最典型的模型。具有結構簡單、全局最優、訓練速度快等優點，很適合解決分類問題。與多層網絡結構類似，它是由三層網絡結構組成的前向神經網絡模型，如圖1所示。它包括輸入層，隱含層和輸出層。輸入層用來將輸入變量xn傳輸到隱含層。隱含層調整神經元的變換函數一徑向基函數R的參數，對輸入做出響應，輸入層與隱含層之間權值為1。而輸出層通過對響應進行加權whn來得到相應的輸出。其中，徑向基函數是非負的非線性函數并且關于中心點對稱。

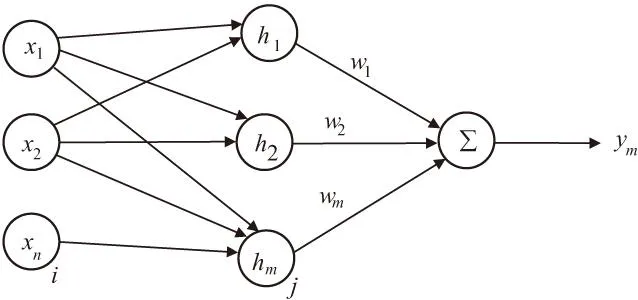
圖1　RBF神經網絡結構

RBF網絡分兩部分：第一部分是輸入層與隱層的連接，對輸入向量進行一次變換，將n維空間的輸入數據變換到m維空間內，即實現X→hj的非線性映射，其表達式為

hj=fj(x1,x2,…,xn)

(8)

式中，j=1，2，…，m,f(x)—RBF神經網絡的徑向基函數。

第二部分是隱層與輸出層的連接，對隱層神經元的輸出線性加權求和得到網絡輸出，即實現hj→ym的線性映射，其表達式為

(9)

式中，ωj—中間層神經元和輸出層神經元的權值；hj—徑向基函數。

2.3　RBF神經網絡控制算法

RBF神經網絡中的徑向基函數有幾種常用的函數形式[6]，選取高斯函數為RBF神經網絡的徑向基函數，其表達式為

(10)

式中，Cj—第j個RBF節點的中心向量；bj—第j節點RBF幅寬參數，且大于零。

當RBF神經網絡的結構確定以后，網絡中需要學習調整的參數包括隱層神經元中心、基寬參數和隱層至輸出層的連接權值。

設k時刻對象的實際輸出為yk，RBF神經網絡的輸出為ym,k，則取網絡的性能指標函數為

(11)

根據梯度下降法，輸出權、中心節點及節點寬度參數的迭代算法為

ωj=ωj,k-1+η(y0,k-ym,k)hj+

α(ωi,k-1-ωi,k-2)

(12)

(13)

bj,k=bj,k-1+Δbj+α(bj,k-1-bj,k-2)

(14)

(15)

cji,k=cjk,k-1+Δcji,k+α(cji,k-1-cji,k-2)

(16)

式中，η—學習速率；α—動量因子。

通過RBF神經網絡辨識，可以得到對象輸出對輸入的敏感度為

(17)

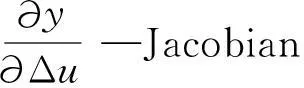
采用增量式PID控制器，誤差為

ek=ydk-yk

(18)

PID三相輸入為

(19)

控制算法為

Δuk=kpek-ek-1+kiek+kdek-2ek-1+ek-2

(20)

3仿真

通過以上分析，在Matlab7.0中編寫仿真程序，考慮到模型的復雜性，直接建立Simulink模型不易，將S函數與Simulink框圖相結合，建立仿真模型，同時單神經元控制與傳統PID算法進行對比，用以驗證單神經元控制的魯棒性[8]。

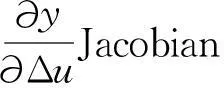
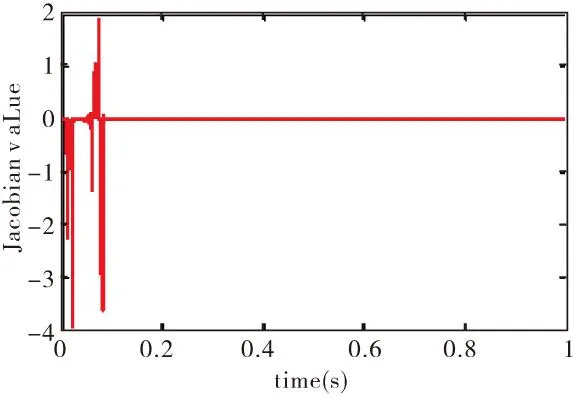
圖2　Jacobian信息變化

圖3　PID參數變化

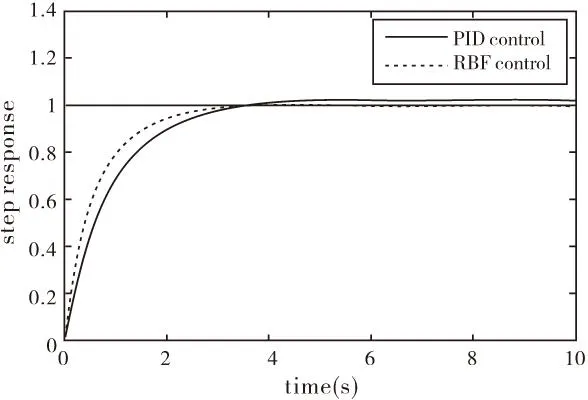
圖4　兩種控制模式下的階躍響應

由圖2、圖3、圖4可以看出，引入RBF神經網絡控制系統的Jacobian信息以及PID參數都進行動態調整，RBF網絡控制與傳統PID控制相比在系統的快速性及準確性上都得到了提高。

4結語

本文針對無刷直流電機控制模式進行了研究。結合無刷直流電機的特性，建立了系統的數學模型，采用了RBF神經網絡控制器，確定了RBF神經網絡的控制模式及控制算法。采用Matlab/Simulink進行仿真。結果表明，與傳統的PID控制相比，基于RBF網絡控制的無刷直流電機系統有更優越的動態性能和穩態性能，系統具有較好的魯棒性。

參考文獻

[1]何玉彬，李新忠.神經網絡控制技術及其應用[M].北京:科學出版社，2000.

[2]楊旭華.神經網絡及其在控制中的應用研究.浙江大學博士學位論文，[D].2004:2-3.

[3]Naira Hovakimyan, Flavio Nardi, Anthony Calise and Nakwan Kim. Adaptive Output Feedback Control of Uncertain Nonlinear Systems Using Single-Hidden-Layer Neural Networks. Neural Networks, 2002, 13(6):1420-1431.

[4]龐明,史儀凱,楊寧.RBF網絡在橫向磁場永磁電機調速系統中的應用[J].計算機測量與控制,2012,20(8):2236-2239.

[5]胡云寶,王加祥,曹鬧昌.基于RBF神經網絡無刷直流電機調速系統[J].微電機,2013,46(1):63-66.

[6]甘敏，彭輝.不同基函數對RBF-ARX模型的影響[J].中南大學學報(自然科學版)，2010，41(6)：2230-2235.

[7]紀志成,沈艷霞,姜建國.基于Matlab無刷直流電機系統仿真建模的新方法[J].系統仿真學報,2003,15(12):1745-1749.

[8]劉金琨.先進PID控制Matlab仿真[M].北京:電子工業出版社,2011.

Application Research of RBF Network to Control System

of Brushless DC Motor

LiShuzhouandDengXiaolong

(1.Department of Automotive Engineering, Hunan Electrical College of Technology, Xiangtan 411000, China；2.China Electric Appliance Science Research Institute, Guangzhou 510300, China)

AbstractThis paper researches control problem of brushless motor. For difficult parameter tuning, large overshoot, long regulation time and poor anti-interference ability of brushless DC motor with conventional PID control system, a mathematical model of brushless DC motor is established, overall design method of RBF neural network control is presented, and RBF network controller based on conventional PID controller is established. The simulative comparison between conventional PID control and RBF network control is carried out by Matlab software, the results show that RBF network controller can dynamically adjust parameters of controller and effectively improve system performance and control effect. The system has strong robustness to parameter perturbation.

Key wordsBrushless DC motor；RBF neural network；Matlab；PID controller

收稿日期：2015-07-28

作者簡介：李書舟男1979年生；碩士研究生，現從事自動控制方面的研究工作.

基金項目：2012年湖南省教育廳高等學校科學研究項目(12c1005)

中圖分類號：TM301.2;TM33

文獻標識碼：A

文章編號：1008-7281(2015)06-0010-004

DOI:10.3969/J.ISSN.1008-7281.2015.06.04