海上蒸發(fā)波導預(yù)測模型選擇方法

周　朋，劉光輝

(解放軍91404部隊，秦皇島 066001)

?

海上蒸發(fā)波導預(yù)測模型選擇方法

周朋，劉光輝

(解放軍91404部隊，秦皇島 066001)

摘要：基于水文氣象條件的蒸發(fā)波導預(yù)測方法是一種常用的蒸發(fā)波導預(yù)測方法。在對現(xiàn)有典型方法的敏感性、穩(wěn)定性、適應(yīng)性以及優(yōu)缺點進行了詳細的比較分析基礎(chǔ)上，提出海上艦艇蒸發(fā)波導預(yù)測模型選擇方法，從理論研究到實驗數(shù)據(jù)的對比分析表明該方法具有明顯的優(yōu)勢，對提高海上蒸發(fā)波導預(yù)測能力具有重要意義。

關(guān)鍵詞：蒸發(fā)波導；預(yù)測模型；選擇方法

0引言

關(guān)于用水文氣象條件預(yù)測蒸發(fā)波導模型，國外許多專家在上世紀70年代初已經(jīng)開始這方面的研究，比較有代表性的預(yù)測模型有美國的 Paulus-Jeske提出并不斷修正的蒸發(fā)波導預(yù)測模型(P-J模式)[1-2]、法國學者Luc Musson-Genon，Sylvie Gauthier和Eric Bruth提出的MGB模式[3]以及美國霍譜金斯大學的S.M.Babin提出的Babin模式[4](也稱A模式)。我國在蒸發(fā)波導預(yù)測上比較有代表性的研究成果有劉成國提出的偽折射率模式[5]和李云波提出的基于海氣通量算法的蒸發(fā)波導診斷模型[6]，他們提出的各種模型都是在Monin-Obukhov相似理論的基礎(chǔ)上得到的，只是應(yīng)用不同。為彌補Monin-Obukhov相似理論在某些條件下不能使用的缺陷，戴福山提出了利用局地相似理論代替Monin-Obukhov相似理論確定蒸發(fā)波導的方法，稱為局地相似蒸發(fā)波導模式[7]。此外，我國的很多學者還對幾種傳統(tǒng)模式在我國海域的適應(yīng)性進行了研究[8]，對蒸發(fā)波導預(yù)測模型在我國海域的應(yīng)用研究起到了促進作用。本文對傳統(tǒng)的基于水文氣象條件預(yù)測蒸發(fā)波導模型進行綜合比較分析，提出了海上艦艇預(yù)測蒸發(fā)波導模型的選擇方法。

1傳統(tǒng)預(yù)測模型

1.1　 Monin-Obukhov相似理論

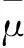
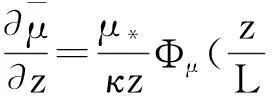
(1)

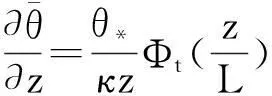
(2)

(3)

式中:μ*、θ*、q*分別為速度特征尺度、溫度特征尺度、水汽特征尺度;κ為Karman常數(shù)，取κ=0.4;L為長度特征尺度，稱為Monin-Obukhov長度;Ζ=z/L,為層結(jié)穩(wěn)定度參數(shù)，當ζ>0時，為穩(wěn)定層結(jié)；ζ<0時，為不穩(wěn)定層結(jié)；ζ=0時，為中性層結(jié);Φμ、Φt、Φq為穩(wěn)定度參數(shù)ζ的函數(shù)，稱為普適函數(shù)，不同研究人員根據(jù)觀測資料給出的普適函數(shù)不同，在中性層結(jié)下均等于1[9]。

對式(3)進行積分，取風速為0，則有：

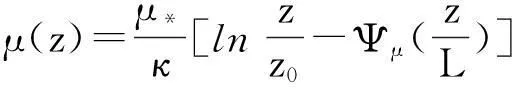
(4)

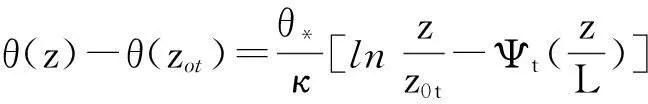
(5)

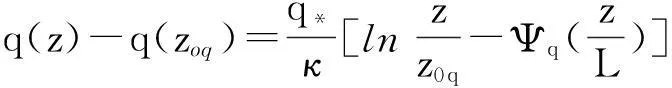
(6)

式(1)～(3)及式(4)～(6)稱為Monin-Obukhov相似理論關(guān)系式。

1.2　傳統(tǒng)模型

(1) P-J模式[7]

在利用P-J模式進行蒸發(fā)波導預(yù)測的過程中，引入了不隨氣壓變化的位折射指數(shù)Np，其關(guān)系式如下[9]:

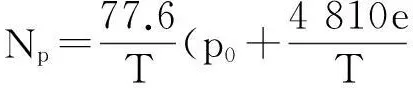
(7)

由Monin-Obukhov相似理論的推導可知，位折射指數(shù)垂直梯度dNp/dz滿足：

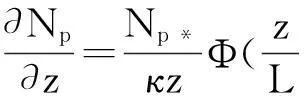
(8)

當位折射指數(shù)梯度等于臨界位折射指數(shù)梯度b時，所對應(yīng)的高度即為蒸發(fā)波導高度d。

因此，在穩(wěn)定或者中性層結(jié)條件下：

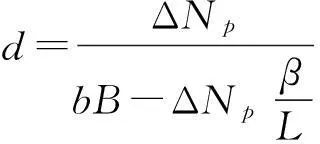
(9)

對于不穩(wěn)定層結(jié)條件下：

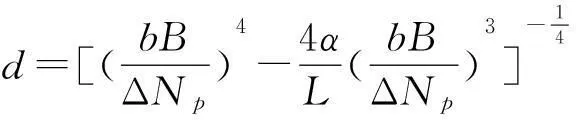
(10)

由于Monin-Obukhov相似理論不能適用于極端穩(wěn)定和極端不穩(wěn)定層結(jié)的海洋大氣環(huán)境，因此，在極端穩(wěn)定層結(jié)環(huán)境下建議d/L應(yīng)不大于1，否則令其等于1；極端不穩(wěn)定層結(jié)環(huán)境下令蒸發(fā)波導高度為零。

(2) MGB模式[3,7,10-13]

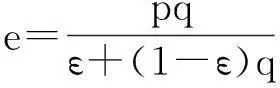
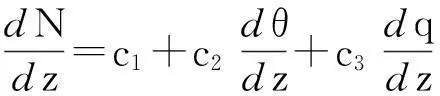
(11)

式中:dθ/dz、dq/dz利用Monin-Obukhov相似理論計算獲得。

與P-J模式不同的地方在于MGB模式在確定L與Ri關(guān)系以及特征尺度參數(shù)θ*、q*時，引用了隱函數(shù)的方法，計算出特征尺度參數(shù)θ*、q*值。最后采用解析方法計算得到波導的高度為：

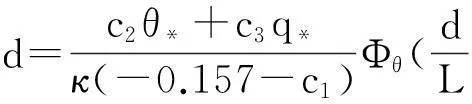
(12)

(3) Babin模式[4,7]

Babin模式最突出的貢獻就是通過引入“陣風性”速度的概念，將Monin-Obukhov相似理論的適用性推廣到了甚低風速條件下。

得到在穩(wěn)定和中性大氣層結(jié)條件下，預(yù)測的波導高度表達式為：

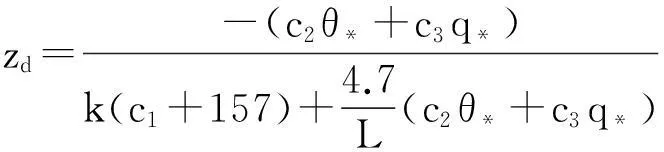
(13)

不穩(wěn)定層結(jié)大氣條件下的波導高度由下式確定：

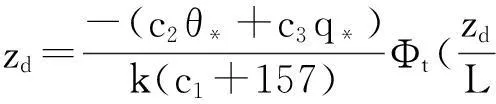
(14)

在極端不穩(wěn)定層結(jié)環(huán)境下，Monin-Obukhov相似理論不再適用，該模式引入了“陣風性”速度ωg，海面平均風速為：

S=μ2+ω2

(15)

(4) 偽折射率模式[5]

偽折射率模式是由我國學者劉成國提出并驗證其可行性的。偽折射率Np定義如下：

Np=4.495e-1.263T

(16)

該模式最終給出的蒸發(fā)波導環(huán)境下大氣修正折射指數(shù)關(guān)系式如下：

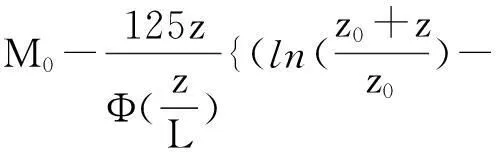
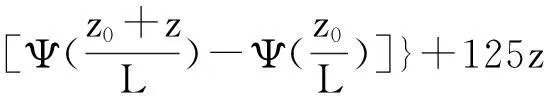
(17)

并采用測得環(huán)境參數(shù)，利用迭代法即可得到波導高度。

(5) Flux模型[3,6]

Flux模式是基于通量算法的蒸發(fā)波導模型的簡稱，模型將相似理論與通量算法相結(jié)合，首先求得各氣象要素垂直廓線分布，進而得到修正折射率廓線，根據(jù)修正折射率最小值對應(yīng)的高度，確定波導高度[12]。

根據(jù)測得的海洋環(huán)境試驗數(shù)據(jù)，該模型通過利用陣性風速ωg來提高適用性：

(18)

可以得到修正折射指數(shù)M的廓線，此時，最小值點所在高度即為蒸發(fā)波導高度。

(6) 局地相似模式和New模式[7]

局地相似蒸發(fā)波導模式和New模式是由我國專家戴福山在總結(jié)前人的基礎(chǔ)之上提出的，既吸收了國內(nèi)外最新模式的優(yōu)點，同時又彌補了Monin-Obukhov相似理論在某些特殊條件下不能適用的不足。

New模式是對Babin模式和局地相似蒸發(fā)波導模式的綜合，由于Babin模式?jīng)]有考慮在強穩(wěn)定層結(jié)條件下Monin-Obukhov相似理論不再適用時的修正，因此，New模式在具有穩(wěn)定層結(jié)海洋大氣環(huán)境時采用局地相似模式算法，具有不穩(wěn)定層結(jié)海洋大氣環(huán)境時采用Babin算法，這樣即利用了Monin-Obukhov相似理論的優(yōu)越性,又對極端條件下的波導預(yù)測進行了修正，因此，New模式是理論上較為優(yōu)秀的模式。

1.3　敏感性分析

海上蒸發(fā)波導對大氣環(huán)境的變化呈現(xiàn)出不同的變化特性，對不同大氣環(huán)境特征的敏感性不同，對氣象條件的敏感度從高到低依次是：大氣濕度、氣海溫差、風速、氣壓[11]。蒸發(fā)波導敏感性最高的海洋大氣環(huán)境因素是大氣濕度，滿足其他海洋環(huán)境因素相同的環(huán)境下，海洋氣象環(huán)境中相對濕度越低時波導的絕對高度越大。蒸發(fā)波導敏感性次之的海洋大氣環(huán)境因素是氣海溫差，隨溫差正值、負值不同而不同：氣海溫差大于零時，氣海溫差差值的大小對波導高度影響很大；當氣海溫差小于零時，氣海溫差差值的大小對波導高度影響較小。風速對蒸發(fā)波導影響的顯著特點是風速越大，波導高度越低，尤其在低風速時影響效果更為明顯。相對而言，蒸發(fā)波導敏感性最小的海洋大氣環(huán)境因素是氣壓。

本文根據(jù)蒸發(fā)波導對不同海洋氣象環(huán)境的敏感性分析，結(jié)合我國周邊海域水文條件特點，對前人研究的不同蒸發(fā)波導預(yù)測模型在海洋大氣環(huán)境中的敏感性、穩(wěn)定性、適應(yīng)性加以總結(jié)與分析，選擇出較適合我國海域氣象環(huán)境特征和艦載通信裝備特點的蒸發(fā)波導預(yù)測模型。

2009年，左雷等人通過理論分析和實測實驗數(shù)據(jù)對P-J模式的敏感性、適應(yīng)性進行了研究，研究結(jié)果表明[4]：該模式計算得到的波導高度對海面風速、大氣相對濕度的變化較為敏感，在其他海洋環(huán)境因素一定時波導高度濕度越大,波導高度越低，與實際蒸發(fā)波導敏感性特征相符，但在風速較大時模型計算結(jié)果的偏差較大；在不穩(wěn)定層結(jié)海洋大氣環(huán)境下，預(yù)測高度對氣海溫差變化較為敏感；相對濕度介于75%～85%之間的小風速海洋大氣環(huán)境下,該模式計算結(jié)果與實際值偏差最小。

田斌等人對解析MGB預(yù)測模式在我國海區(qū)適應(yīng)性也做了相關(guān)的研究，綜合比較分析可以得出模型預(yù)測結(jié)果對氣海溫差的敏感性最大，其次是相對濕度和風速，氣壓敏感性最小；越接近中性層結(jié)，模型預(yù)測得到的波導高度值與實測真實值越接近。但國家海洋環(huán)境預(yù)報中心李詩明對MGB模式的研究可以看出，模型預(yù)測結(jié)果對輸入變量噪聲的敏感性很強，因此限制了該模式在業(yè)務(wù)上的使用[1]。

Babin模式最突出的特點是采用了鹽度修正來計算飽和水汽壓的值，并在一定程度上克服了Monin-Obukhov相似理論的局限性，將其適用性延伸至低風速的極端穩(wěn)定層結(jié)海洋大氣環(huán)境下。田斌等對該模式在我國海域的適應(yīng)性及敏感性進行了分析和實驗對比，結(jié)論為：該模式對氣海溫差、風速及大氣相對濕度等海洋氣象環(huán)境因素的變化都具備一定的敏感性，對水文氣象觀測系統(tǒng)的傳感器具有最低精度要求[3]。

劉成國在提出偽折射率模型的同時對其敏感性和實驗結(jié)果進行了分析[5]，計算機仿真結(jié)果表明:氣海溫差滿足小于-1℃的海洋氣象環(huán)境下，其對波導高度的影響不明顯;而當氣海溫差在0～2℃時，影響變化顯著，但變化規(guī)律不明顯；南海海上實驗利用測量儀器測得的蒸發(fā)波導在各種天氣條件下的發(fā)生概率與利用偽折射率模型預(yù)測得到的波導發(fā)生概率相近,并且吻合度達到了52%以上。

Flux模式與Babin模式計算機理大致相同，都是通過海氣通量算法計算Monin-Obukhov相似理論的相關(guān)參數(shù)，并且都引入了“陣風性”對在風速為零情況下Monin-Obukhov相似理論進行了修正，因此這2種模式的特點相似，在實際運用中根據(jù)大氣環(huán)境條件和二者在其他方面的差異考慮即可。

在研究蒸發(fā)波導預(yù)測模型過程中，許多專家學者對各模型在海洋大氣環(huán)境下的敏感性、穩(wěn)定性等方面進行了比較分析，得出了許多的研究成果。戴福山分別于1999年和2000年先后5次進行海上試驗，實際觀測海洋水文氣象數(shù)據(jù)，研究不同預(yù)測模型預(yù)測得到的波導高度，得出如下結(jié)論[7]：

對于較常見的不穩(wěn)定層結(jié)、中性層結(jié)和弱穩(wěn)定層結(jié)的海洋大氣環(huán)境中，各模型預(yù)測得到的波導高度大致相同；對于晴好天氣里經(jīng)常發(fā)生強穩(wěn)定層結(jié)海洋大氣環(huán)境中，只有基于局地相似理論的local1模型和P-J模型預(yù)測結(jié)果比較準確，但在強穩(wěn)定層結(jié)海洋大氣環(huán)境中Monin-Obukhov相似理論是不適用的，P-J模式采用了人為修正。

評估電磁波傳播損耗方面，當氣海溫差大于零時或者強穩(wěn)定層結(jié)大氣環(huán)境下，基于局地相似理論的local1模式可以較好地滿足精確計算傳輸損耗的需要，P-J模式?jīng)]有顯示出超視距傳輸現(xiàn)象，其他模式結(jié)果也不夠準確；在弱穩(wěn)定層結(jié)條件、中性層結(jié)以及不穩(wěn)定層結(jié)的海洋大氣環(huán)境下,各模型之間預(yù)測得到的波導高度差異較小；而在風速較小時，Babin模式的預(yù)測結(jié)果較好。

王向敏結(jié)合我國海域?qū)崪y數(shù)據(jù)對Babin模式與偽折射率模式進行了比較分析[1]，在風速較小時，Babin模式的穩(wěn)定性明顯優(yōu)于偽折射率模式；兩模式對濕度和溫度的敏感性相同，但偽折射率模式對風速的敏感性較小。宋偉利用實驗數(shù)據(jù)對P-J模式和Babin模式適應(yīng)性進行了對比分析，分析結(jié)果表明[14]：按層結(jié)穩(wěn)定性劃分時，P-J模式的準確性要好于Babin模式；而當風速較小時，Babin模式計算的波導高度誤差要小于P-J模式，進一步驗證了低風速環(huán)境下Babin模式較其他方法預(yù)測結(jié)果的準確性更好。郭相明等人指出[15]：在具備穩(wěn)定層結(jié)的海洋大氣環(huán)境中，P-J模式預(yù)測精度最優(yōu)；在不穩(wěn)定層結(jié)的海洋大氣環(huán)境中，MGB模式預(yù)測精度最低，其他模式相差不大，并提出在蒸發(fā)波導預(yù)測上優(yōu)先考慮P-J模式。

2海上艦艇預(yù)測蒸發(fā)波導模型

2.1　預(yù)測模型選擇方法

通過對基于水文氣象環(huán)境傳統(tǒng)預(yù)測模型的研究及前人對各個方法的比較分析可以看出，傳統(tǒng)的預(yù)測模型在分析檢測波導所處的近海面空間范圍內(nèi)的氣象因素特征是基于Monin-Obukhov相似理論或局地相似理論來構(gòu)建的；只是蒸發(fā)波導高度計算方法、普適函數(shù)選取依據(jù)、參量特征尺度等其他因素的選擇上存在差異。本文在此基礎(chǔ)上，根據(jù)海上艦艇裝備實際情況，提出采取如下方式利用水文氣象條件預(yù)測蒸發(fā)波導：

(1) 在強穩(wěn)定層結(jié)海洋大氣環(huán)境時，選取局地相似理論的蒸發(fā)波導預(yù)測模式;

(2) 在弱穩(wěn)定層結(jié)、中性層結(jié)以及不穩(wěn)定層結(jié)海洋大氣環(huán)境時選取P-J模式;

(3) 在極端不穩(wěn)定層結(jié)海洋大氣環(huán)境時選取Babin模式。

Monin-Obukhov相似理論不滿足強穩(wěn)定層結(jié)海洋大氣環(huán)境時的應(yīng)用條件，P-J模式在此情況下需考慮人為修正，不適于艦艇裝備及人員實際情況，而局地相似理論適用于整個近地層，可以彌補Monin-Obukhov相似理論的缺陷，因此本文在強穩(wěn)定層結(jié)海洋大氣環(huán)境時選取基于局地相似理論的蒸發(fā)波導預(yù)測模式。

極端不穩(wěn)定層結(jié)多發(fā)生在晴好的海洋大氣環(huán)境中，通過上述各個模式的研究與比較分析，Babin模式將Monin-Obukhov相似理論推廣到甚低風速海洋大氣環(huán)境下、風速較小的大氣環(huán)境時，該模型預(yù)測效果最優(yōu)。

其它大氣層結(jié)的海洋大氣環(huán)境下選用P-J模式。P-J模式是目前蒸發(fā)波導預(yù)測方面應(yīng)用最成功的模型之一，美國研究人員將其集成到某微波傳播預(yù)報系統(tǒng)中，作為業(yè)務(wù)化預(yù)報模式投入實際應(yīng)用。可以看出，在P-J模式的應(yīng)用上有著成熟的先例與經(jīng)驗，而且通過前面的比較分析，在弱穩(wěn)定層結(jié)、中性層結(jié)以及不穩(wěn)定層結(jié)的海洋大氣環(huán)境時，該模式除在某些特定水文氣象環(huán)境下具有優(yōu)勢外，其他環(huán)境條件下并無明顯缺陷，因此，建議使用P-J模式。

2.2　對比分析

為進一步驗證本文提出的蒸發(fā)波導預(yù)測模型選擇方法的有效性，采用戴福山于2000年1月14日南海試驗的海面水文氣象數(shù)據(jù)及部分模型計算得到的蒸發(fā)波導(見參考文獻[7]的238-239頁)高度加以分析。實驗數(shù)據(jù)如表1、表2所示。

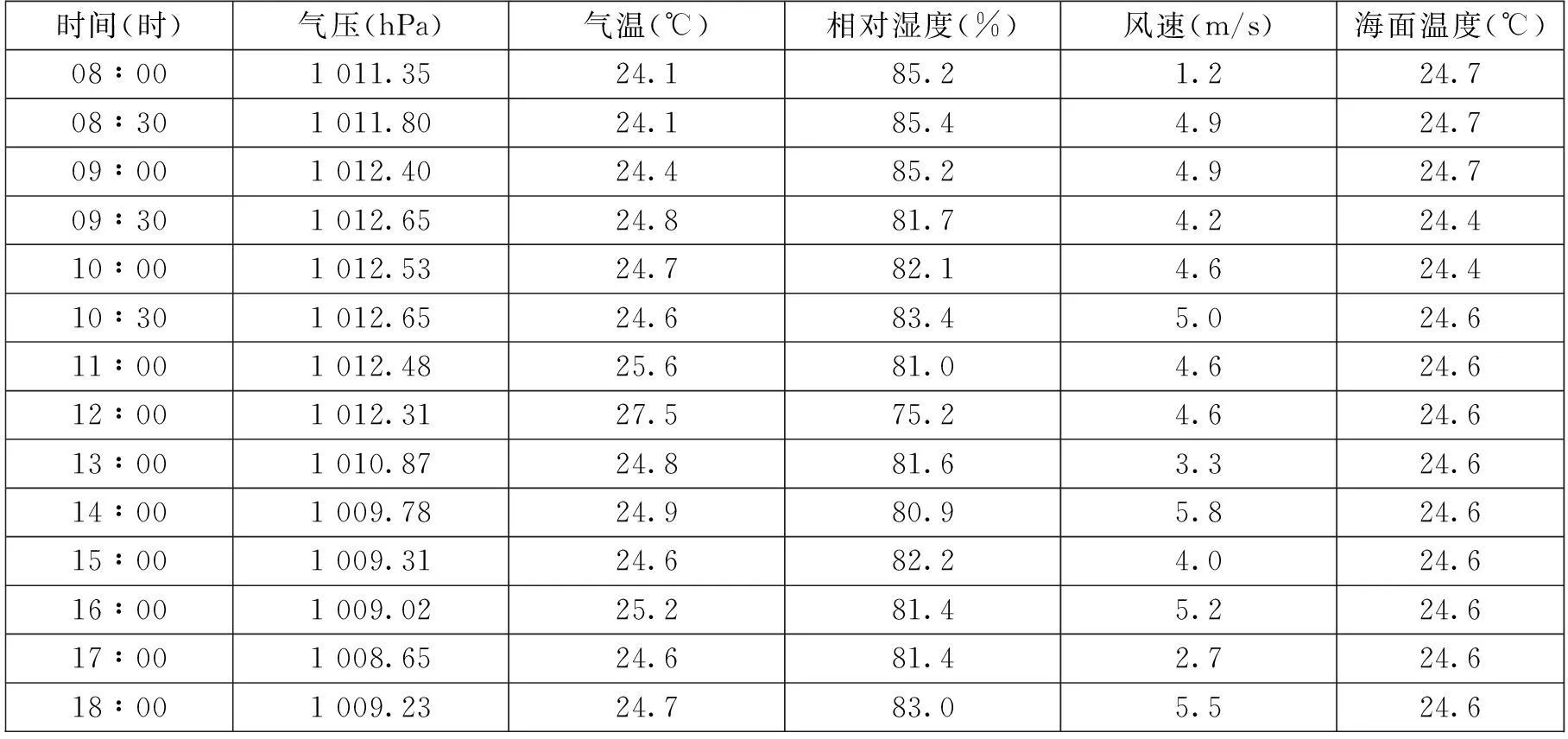
表1　2000年1月14日南海試驗海面水文氣象觀測數(shù)據(jù)

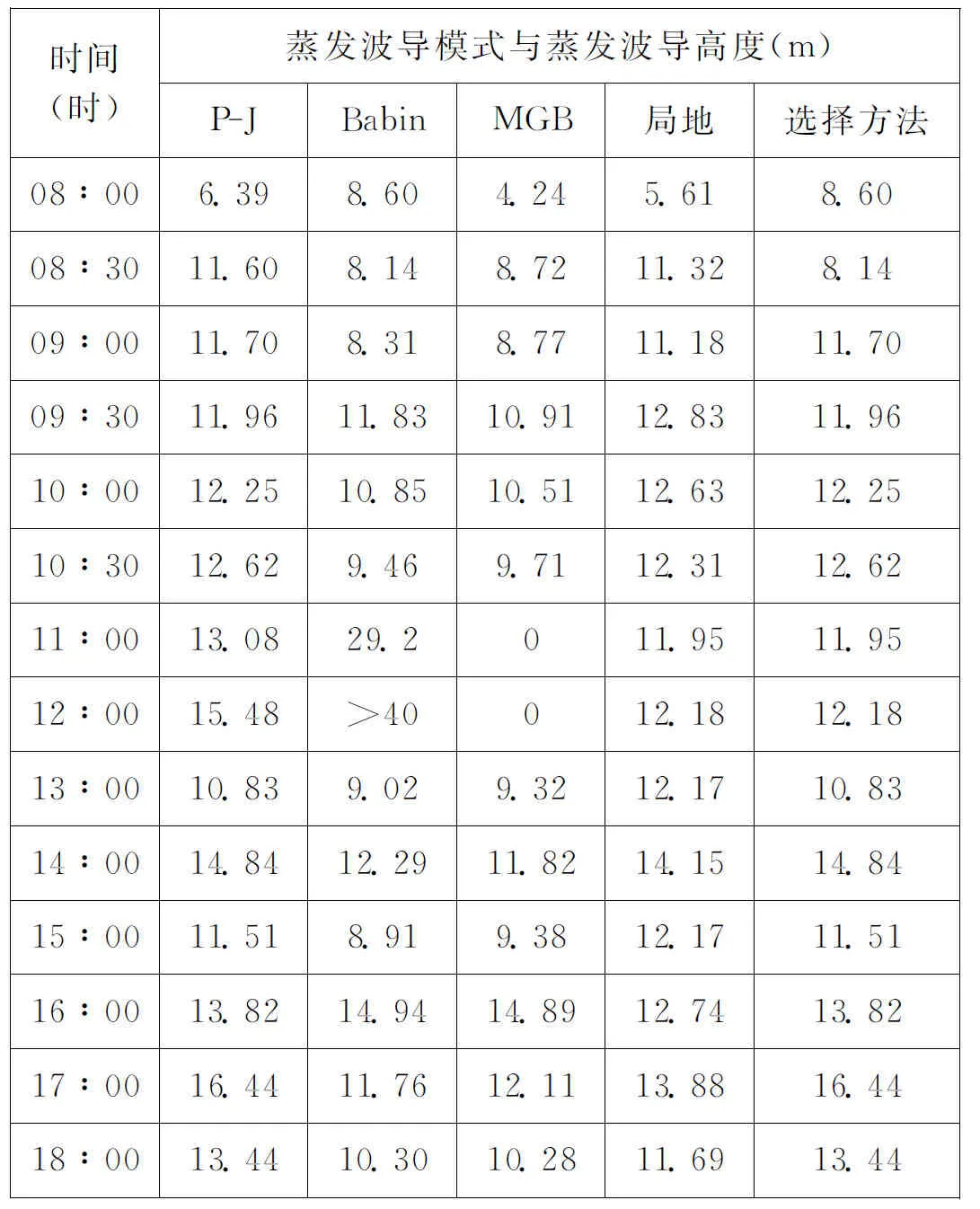
表2　各模型不同時刻預(yù)測蒸發(fā)波導高度值

利用各預(yù)測模式實際預(yù)測的波導高度如表2和圖1所示。可以看出，在08∶00時刻，海面氣海溫差小于0，處于不穩(wěn)定層結(jié)海洋大氣環(huán)境下，且風速較小。除Babin模式外，其他模式給出的波導高度明顯偏低，進一步驗證了Babin模式在低風速氣象環(huán)境下的優(yōu)越性。此時，本文提出的選擇方法與Babin模式相同。與其他時刻相比，在11∶00和12∶00時刻各模型給出的蒸發(fā)波導高度差異較大，Babin模式給出的高度明顯偏高，而MGB模式明顯偏低，本文方法與局地相似蒸發(fā)波導模式相同，且與P-J模式相接近。在這2個時刻，氣溫顯著高于海面水溫，處于強穩(wěn)定層結(jié)海洋大氣環(huán)境，驗證了在強穩(wěn)定層結(jié)海洋大氣環(huán)境時Monin-Obukhov相似理論不再適用，以該理論為基礎(chǔ)的預(yù)測模型無法準確預(yù)測出波導高度。

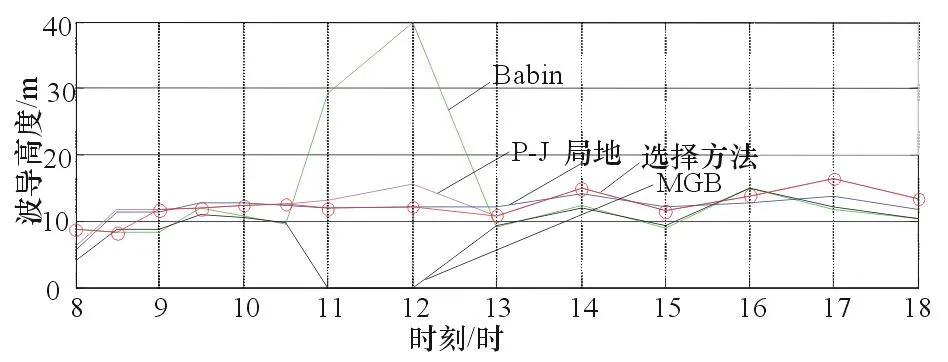
圖1　蒸發(fā)波導高度

P-J模式預(yù)測結(jié)果較為接近，是由于該模式在強穩(wěn)定層結(jié)條件下做了人為修正，而基于局地相似理論的蒸發(fā)波導模式?jīng)]有任何修正，因此，認為在強穩(wěn)定層結(jié)海洋大氣環(huán)境時基于局地相似理論的蒸發(fā)波導模式可以更準確地預(yù)測得到波導高度。除上述時刻其他時間外，各模式預(yù)測得到的波導高度大致相同，且變化趨勢相同。本文提出的選擇方法與P-J模式相同，主要考慮P-J模式作為成功應(yīng)用的先例，計算得到的蒸發(fā)波導高度較為平緩，穩(wěn)定性較好。綜上所述，本文提出的海上艦艇預(yù)測蒸發(fā)波導模型選擇方法，從理論研究到實驗數(shù)據(jù)的對比分析表明是一種較好的蒸發(fā)波導預(yù)測模型選取方法。

3結(jié)束語

在基于水文氣象條件的方法中，本章對現(xiàn)有的典型方法進行了介紹，并對他們的敏感性、穩(wěn)定性、適應(yīng)性以及自身的優(yōu)缺點進行了詳細的比較分析，提出了海上艦艇預(yù)測蒸發(fā)波導模型選擇方法，從理論研究到實驗數(shù)據(jù)的對比分析表明該方法具有明顯的優(yōu)勢。

參考文獻

[1]Jeske H.The state of radar-range prediction over sea[A].Part Ⅱ,AGARD-CP-70[C],1971:1-10.

[2]Paulus Richard A.Specification for evaporation duct height calculations[J].Naval Ocean Systems Center,1989(4):139-148.

[3]Lue Musson-Genon,Sylvie Gauthier,Eric Bruth.A simple method to determine evaporation duet height in the sea surface boundary layer[J].Radio Science,1992,27(5):635-644.

[4]Babin Steven M,Young George S,Carton James A.A new model of the oceanic evaporation duct[J].Journal of Applied Meteorology,1997,36(3):193-204.

[5]劉成國,黃際英,江長蔭,等.偽折射率和相似理論計算海上蒸發(fā)波導剖面[J].電子學報,2001,29(7):970- 972.

[6]李云波,張永剛,唐海川,等.基于海氣通量算法的海上蒸發(fā)波導診斷模型[J].應(yīng)用氣象學報,2009,20(5):628-633.

[7]戴福山,李群,董雙林,等.大氣波導及其軍事應(yīng)用[M].北京:解放軍出版社,2002.

[8]成印河,趙振維,何宜軍,等.大氣波導過程數(shù)值模擬研究[J].電波科學學報,2009,24(2):259-264.

[9]李梁, 張海勇,闞榮才.Monin-Obukhov理論在蒸發(fā)波導PJ模式中的應(yīng)用[J].現(xiàn)代防御技術(shù),2014(2):89- 94.

[10]漆隨平,王東明,郭顏萍,等.海上蒸發(fā)波導的預(yù)測方法綜述[J].海洋通報,2012,31(3):347-353.

[11]繆剛.海上寬帶超視距蒸發(fā)波導微波通信系統(tǒng)的建模與分析[J].硅谷,2012(6):188-189.

[12]李詩明,陳陟,喬然,等.海上蒸發(fā)波導模式研究進展及面臨的問題[J].海洋預(yù)報,2005,22(S0):128-138.

[13]王向敏.海上大氣波導的預(yù)測方法[D].南京：南京信息工程大學,2007.

[14]宋偉,田斌,周沫,等.蒸發(fā)波導預(yù)測模型研究[J].華中科技大學學報(自然科學版),2013,41(5):52-56.

[15]郭相明,康士峰,張玉生,等.蒸發(fā)波導模型特征及其適用性研究[J].海洋預(yù)報,2013,30(5):75-83.

Prediction Model Selection Method of Maritime Evaporation Wave-guide

ZHOU Peng，LIU Guang-hui

(Unit 91404 of PLA,Qinhuangdao 066001,China)

Abstract:The prediction method of evaporation wave-guide based on hydrological meteorological condition is a common method.This paper presents the prediction model selection method of maritime ship evaporation wave-guide based on detailed comparison and analysis of existing typical methods from sensitivity,stability,adaptability and advantage/disadvantage.The comparison and analysis of theoretical study and experimental data show that the method has obvious advantages,which is of important meaning to raise the prediction ability of maritime evaporation wave-guide.

Key words:evaporation wave-guide;predication model;selection method

收稿日期:2015-04-08

DOI:10.16426/j.cnki.jcdzdk.2015.05.011

中圖分類號：TN928

文獻標識碼：A

文章編號：CN32-1413(2015)05-0046-06