談中考試題中蘊含的數學思想方法

萬里

摘 要：在進行數學解題的時候，合理地采用數學解決方法，并且貫穿一定的思想方法能夠取得事半功倍的效果。數學思想方法是對數學概念、知識、方法的全方位總結和認識，它是數學知識的精髓所在，是在進行數學解題過程中的強大工具。以近年江蘇省13市的中考試題為例，簡要分析了初中數學解題的主要思想方法。

關鍵詞：中考試題；數學；思想方法

通過對數學思想方法的合理應用，學生可以在很大程度上簡化數學問題的難度，使原本復雜的問題變得更加簡單，抽象的問題變得更加具象。近年來隨著我國教育改革的不斷深化，不管是在初中數學課堂的教學過程中還是在中考數學試題的命題中都十分重視數學思想方法。學生利用數學思想方法的能力能夠反映他們對知識點的理解和應用能力，能夠展示他們解題的思維能力，是衡量學生數學解題能力的重要依據。

一、數學思想方法分析

（一）數形結合思想方法

在數學學習過程中，最常碰到的就是數與形的問題，其中數和形之間是存在密切聯系的，數是形的一種抽象概括，而形則是數的一種具體表達。這就告訴我們在進行數形問題的解決時，可以將這兩者進行轉換，也就是說數的問題可以用形來解決，而同樣形的問題也可以借助數來計算。在進行數學問題解答的時候我們要把抽象的數學語言和具體的圖形結合起來，利用圖形作為輔助工具進行問題的解答。

（二）分類討論思想方法

當一道數學試題具有不唯一解的時候，就需要應用到另外一種數學解題思想方法，那就是分類討論思想方法。學生在進行解題的時候可以按照一定的原則把問題所涉及的情況分成若干類別，然后按照類別進行逐一的討論，在全部的類別討論完成之后，再把這些類別所得出來的結論進行匯總就是問題的完整答案。這種思想方法的本質其實就是“化整為零”，把復雜的問題拆開進行討論，這種數學思想方法的一般應用步驟如下：首先仔細閱讀問題，確定一個正確的分類標準；其次，針對特定的問題進行分析，按照設定好的分類標準對所有情況進行分類，要保證做到分類不重復不遺漏；然后，對所有的情況進行分別討論，逐步得出結論；最后，將各類的結論進行分析和匯總，重復的結論進行合并，最終得出問題的完整答案。

（三）等價轉化思想方法

把未知的問題轉變成為已知問題，把復雜的數學問題簡單化所應用到的數學思想方法就是轉化思想。轉化思想讓學生從問題的另外一個角度進行考慮，通常這種思想方法能夠把非常規的問題轉變成為常規的問題，把復雜的問題轉化成為簡單的問題，從而能夠使得問題迎刃而解，極大地節省了學生解題過程中所需要花費的時間。

（四）配方法以及待定系數法

在初中數學學習過程中，配方法的使用是非常頻繁的，利用這種數學思想方法可以解決一些理論性或者比較實際的問題。在有關方程計算的問題中對配方的應用比較多，比如說利用它可以推導一元二次方程或者是求根公式；計算方程的極值點，并且大體描繪出方程的圖像輪廓等。在進行方程配方的時候一定要謹記一定規律，那就是在進行配方的時候方程兩邊要加上一次項系數一半的平方。待定系數法就是利用特定的字母將數學問題的未知量表示出來，然后通過帶入未知量，求解方程組從而求出待定系數的大小，使問題得以解決。

二、中考試題中數學思想方法的具體應用

下面就以2015年泰州市中考數學試題的第14題進行簡要分析，來探究具體數學思想方法的應用。題目如下：

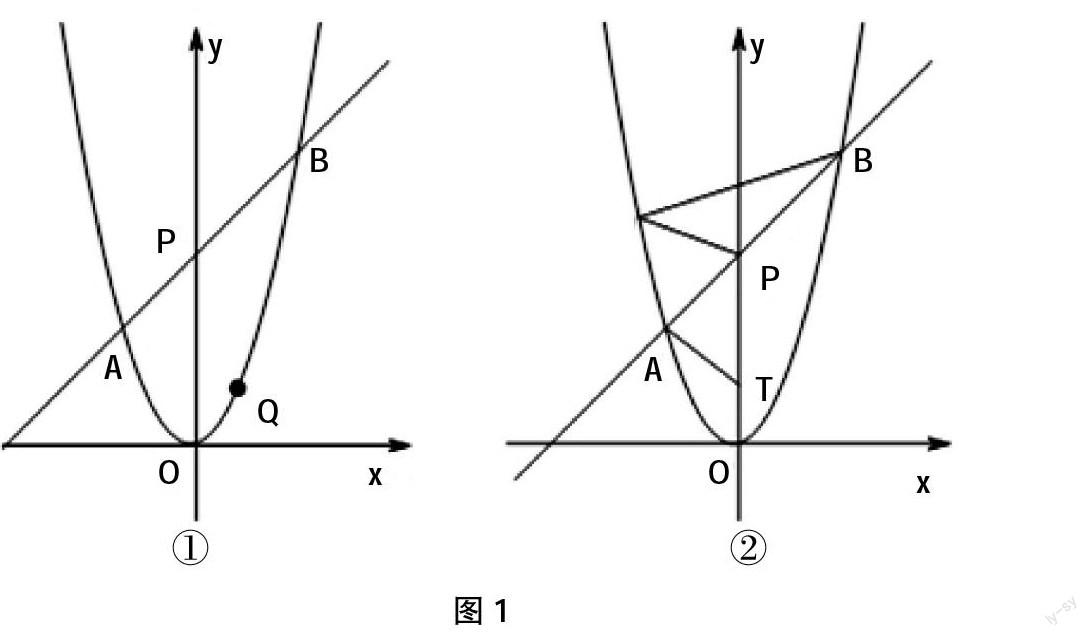
如圖1，在平面直角坐標系xOy中，將拋物線y=x2的對稱軸繞著點P（0，2）順時針旋轉45°后與該拋物線交于A、B兩點，點Q是該拋物線上的一點。

（1）求直線AB的函數表達式；

（2）如圖1①，若點Q在直線AB的下方，求點Q到直線AB的距離的最大值；

（3）如圖1②，若點Q在y軸左側，且點T（0，t）（t<2）是直線PO上一點，當以P、B、Q為頂點的三角形與△PAT相似時，求所有滿足條件的t的值。

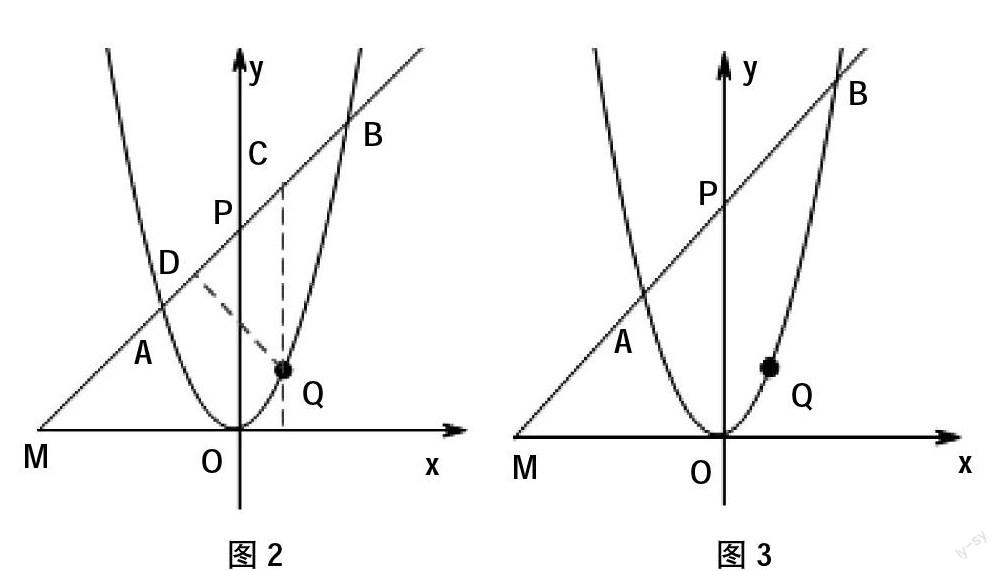
學生在進行第一問求解的時候，首先需要做的就是根據旋轉的性質得到等腰直角三角形PMO，然后再根據已知條件∠OPA=45°以及P（0，2）就可以很輕松地得出M（-2，0）。進而應用待定系數法即可求得直線AB的解析式，所得的POM如圖2所示。

然后在進行第二問的求解時，作出如圖3所示的圖形，具體做法就是過點Q作x軸的垂線QC，交AB于點C，再過點Q作直線AB的垂線，垂足為點D，根據題目中所給的已知條件就可以得出三角形QCD為等腰直角三角形，所以就可以得出，QD=QC然后再設Q點的坐標，得出QC點之間的關系式，根據QD與QC之間的關系進一步求出QD的表達式，最后充分應用二次函數的最值定理就能夠得出想要的答案。在解答第三問的時候，學生需要注意，因為它所涉及的情況不唯一，會存在∠BPQ=45°，∠PBQ=45°，∠PQB=45°這三種情況，學生需要對這三種情況進行分別討論，然后把得出的結果進行匯總，才是問題的最終答案。在解答這道問題的時候上面所提到的數學思想方法基本都有應用，當然題目還涉及線動旋轉和相似三角形存在性問題、曲線上點的坐標與方程的關系、等腰直角三角形的判定和性質、二次函數最值求解問題，以及三角形的勾股定理和方程思想都有所涉及。

綜上所述，我們知道數學思想方法是幫助學生解決數學問題的重要指導性思想和工具，它是數學知識的靈魂所在。不過學生要想具備優秀的數學思想方法，并不是一蹴而就的，這種思想方法的學習過程是潛移默化的，它需要學生在數學學習過程中不斷總結和積累。當學生掌握了數學思想方法之后，還要注意對它們的鞏固和應用，保證學生在利用數學思想方法進行解題的時候可以做到信手拈來。

參考文獻：

[1]劉金英，貫忠喜，何志平.2011年中考數學試題分類解析：數與代數[J].中國數學教育，2012（01）.

[2]景敏，張美玲，劉見樂，等.中考數學試題分類解析（一）：數與代數[J].中國數學教育，2011（01）.

[3]張志英.例談中考試題中數學思想方法的滲透[J].中學生數理化：教與學，2012（04）.

編輯 謝尾合