散粒貨物對敞車靜側壓力的分布規律研究

趙方偉，付秀琴，張 弘，張澎湃，叢 韜，張關震，吳 斯

（中國鐵道科學研究院 金屬及化學研究所，北京100081）

散粒貨物對敞車靜側壓力的分布規律研究

趙方偉，付秀琴，張 弘，張澎湃，叢 韜，張關震，吳 斯

（中國鐵道科學研究院 金屬及化學研究所，北京100081）

為研究散粒貨物對敞車的靜側壓力分布規律，以滿載散粒煤的C80B型敞車為研究對象，采用修正的D－P模型數值模擬散粒煤的本構模型，通過簡化幾何模型和有限元方法，建立了整車三維數值離散模型。在車體與散粒煤的接觸面均設置柔柔接觸，采用修正的硬接觸關系模擬其法向接觸行為，并引入“彈性滑移變形”模擬其切向摩擦行為。對車體靜側壓力進行數值計算，并將結果與庫侖土壓力理論計算結果進行對比。結果表明：散粒煤中部沉降量最大，沉降量沿裝貨高度呈非線性分布；側壓力沿敞車墻高非線性分布，且在頂部位置不為零；散粒煤對敞車的側壓力沿車長和車寬方向非均勻分布，呈非線性分布。

敞車；散粒貨物；D－P模型；數值模擬；側壓力

在鐵路運輸的貨物中，煤、礦石、礦材、糧食等以散裝形式運送的顆粒狀貨物占總的貨物發送量的七成以上。隨著鐵路貨運的提速和重載化，散粒貨物對敞車的作用問題變得日益突出。針對散粒貨物對敞車的作用問題，尤其對端、側墻的壓力問題，國內外學者做了大量研究。

美國鐵道學會AAR標準［1］按Rankine土壓力公式計算散體作用于敞車端、側墻的壓力，認為其壓力分布是線性三角形分布。我國TB／T 1335－1996《鐵道車輛強度設計及試驗鑒定規范》［2］中規定的散粒煤對敞車端、側墻的計算方法是基于二維計算模型，認為散粒煤對端、側墻的壓力沿車長和車寬均勻分布。近些年，隨著CAE技術的發展，散粒煤對敞車側壓力的研究引入了新的手段和方法。文獻［3］在有限元軟件中建立二維有限元模型，以M－C屈服準則模擬散粒貨物塑性模型，研究了散體對敞車端墻的作用規律。文獻［4］采用二維模型分析了極限狀態時，散粒煤對車體端墻的側壓力分布。實踐證明，二維計算模型不能反映真實情況。文獻［5］建立了三維有限元計算模型，但采用的是集中質量法，以剛性桿單元模擬散粒貨物對敞車的作用情況，無法真實的模擬散粒貨物的流動性，誤差較大。文獻［6］考慮了端、側墻加強橫帶的影響，以C70型敞車車體真實結構為研究對象，建立三維有限元模型，分析了散粒煤對車體端、側墻的側壓力，但對于結構不同的敞車車體而言，不具有普遍規律性。

為了更準確的模擬散粒貨物沿端、側墻兩個方向的側壓力分布規律，以C80B型專用敞車為原型，簡化并建立整車三維數值模型，對其進行數值仿真計算。散粒貨物選取煤作為分析對象，采用修正的D－P準則，對車體端、側墻靜側壓力進行數值模擬，分析散粒貨物對敞車靜側壓力的分布規律。研究的成果可以為我國運煤敞車端、側墻壓力校核標準的改進和完善提供理論依據，也可以為車輛的結構設計優化提供參考。

1 數值模型

1.1 散粒煤本構模型

根據土力學理論，散粒煤屬于典型的顆粒狀松散貨物，本構模型一般選擇M-C模型、D－P模型和修正的D－P模型。

（1）Mohr-Coulomb（M－C）理想彈塑性模型

Coulomb在土的摩擦試驗、壓剪試驗和三軸試驗的基礎上，于1773年提出了庫侖破壞準則，認為當土體某平面上剪應力達到某一特定值時，便進入屈服［7］。其準則方程形式一般為

式中c為土的黏聚力，φ為土的內摩擦角，σn為屈服面上的正應力。該方程通過試驗確定。

在π平面上的屈服曲線為一封閉的非正六邊形。現在，M－C準則仍被廣泛應用，該準則在π平面上的拉、壓軸相等時即為廣義Tresca準則。M－C準則比較符合試驗，但是它的缺點在于三維應力空間中的屈服面存在角點奇異性，且沒有考慮中間主應力σ2的影響。

（2）Drucker-Prager（D－P）模型

1952年Drucker和Prager首先把不考慮中間主應力σ2影響的Coulomb屈服準則與不考慮凈水壓力影響的Mises準則聯系在一起，提出廣義Mises理想塑性模型，即D－P模型［8］。D－P模型的屈服面方程為

D－P屈服函數所表示的屈服面在π平面上是一個圓，更適合數值計算。但是作為近似計算，D－P模型仍被廣泛應用。

（3）擴展的Drucker-Prager（D－P）模型

該模型可以用來模擬摩擦材料，典型的是粒狀巖土材料及表現壓力相關的屈服材料；還可以用來模擬抗壓屈服強度大于抗拉屈服強度的材料，且容許材料等向硬化或軟化。修正的D－P模型屈服面方程為

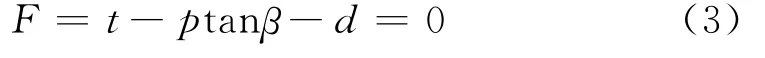
式中t＝q／2［1＋1／k－（1－k）（r／q）3］，q為偏應力，k為三軸拉伸強度與三軸壓縮強度之比，反映了中間主應力σ2對屈服的影響，r為第3偏應力不變量，p為平均應力，β為材料的內摩擦角，d為材料的粘聚力。

修正的D－P模型屈服面在π面上的圖形為光滑過渡曲線，且考慮了平均主應力的影響。

由于在鐵路運輸過程中，散粒煤主要承受壓應力，受壓屈服強度遠大于受拉屈服強度，因此，選取修正的D－P模型來描述散粒煤本構模型更合適。散粒煤本構模型參數如表1所示。

表1 散粒煤本構模型參數

1.2 有限元模型

C80B專用敞車車體主要是由鋼板焊接而成，車體內部長、寬、高分別為10 550 mm，2 976 mm，2 600 mm。為研究散粒煤對敞車側壓力的規律，將C80B敞車簡化為沒有頂面的立方體薄板結構，單元類型選取板殼單元Shell63，網格劃分的精度直接關系到有限元計算的準確性，采用等尺寸單元進行劃分。通過網格離散建立仿真離散模型，如圖1所示。根據實際情況，僅在敞車底板處設置全約束邊界條件。車體為鋼結構，材料參數設置為：密度7.8×10－9t／mm3，彈性模量2.1×105 MPa，泊松比0.3。

圖1 車體仿真離散模型

不考慮顆粒物性參數、粒徑形狀對結果的影響，只研究整個散體所表現出來的屬性，根據連續介質理論，把散粒介質近似為連續介質［9］。因此，采用實體單元模擬散粒煤，單元類型選取Solid45六面體單元。設定散粒煤的裝貨高度與敞車車體的內高相同。散粒煤仿真離散模型見圖2。計算載荷為車體與散粒煤的自重。

圖2 散粒煤仿真離散模型

1.3 接觸面力學模型

在敞車車體底面、端墻和側墻均設置接觸對，接觸類型選擇柔柔接觸，剛度較大的車體表面作為接觸主面，散粒煤表面為從面［10］。在車體與散粒煤的三維建模分析中采用面面接觸方法模擬車體與散粒煤的接觸行為。

（1）接觸面的法向模型

對于接觸問題，車體與散粒煤只有在壓緊狀態時才傳遞法向應力p，存在間隙時不傳遞法向壓力，這種法向行為被稱為硬接觸［11］。硬接觸在計算中限制了可能發生的穿透現象，但當接觸條件從間隙為正到間隙為零時，接觸壓力會發生劇烈的變化，有時使得接觸計算很難收斂。

根據巖土工程理論，認為車體與散粒煤接觸面具有黏聚力，在脫開之前能承受一定的拉力，這時可采用修正硬接觸關系。為保證接觸計算收斂，可以指定一個能承受的拉力pmax，在拉力超過該值后才認為接觸面脫開，接觸壓力變為零；也可以指定一個適當的過盈量hmax，當過盈量超過hmax后才認為接觸面從脫開轉為閉合。

（2）接觸面的摩擦模型

當接觸面處于閉合狀態時，接觸面可以傳遞摩擦力。若摩擦力小于某一極限值τcrit時，接觸面處于黏結狀態；若摩擦力大于τcrit之后，接觸面開始出現相對滑動變形，此時處于滑移狀態［12］。在理想狀況下，車體與散粒煤接觸面在滑移狀態之前沒有剪切變形，在仿真計算時容易導致不收斂。需要對計算模型進行修正，通過引入“彈性滑移變形”，允許接觸表面黏結在一起時發生少量相對滑移變形。根據車體與散粒煤接觸面上單元的長度確定彈性滑移變形，一般設置為單元典型長度的0.5%，然后選擇罰摩擦方法中的剛度進行計算。

2 位移響應分析

2.1 散粒煤位移響應

散粒煤的垂向位移響應結果，如圖3所示。分別選取散粒煤端墻中部、側墻中部和端側墻連接處3個位置的垂向一排節點，以散粒煤頂部為起點，描繪垂向位移響應曲線，如圖4所示。

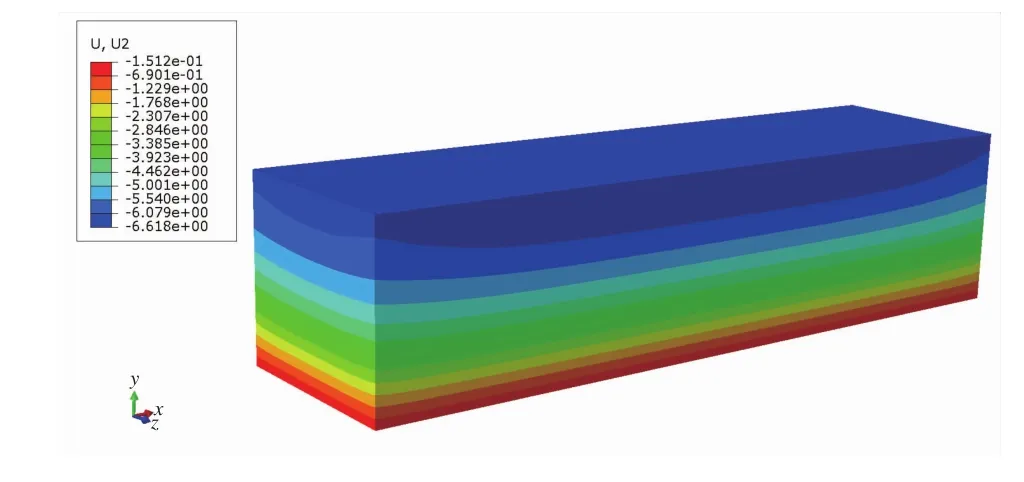
圖3 散粒煤垂向位移響應云圖

圖4 散粒煤垂向位移曲線

由圖3可見，在重力作用下散粒煤發生了沉降，散粒煤中部垂向位移最大，最大值為6.618 mm。由于散粒煤與車體端、側墻摩擦力的作用，靠近車體端、側墻的散粒煤沉降量小于內部。由圖4可以看出，散粒煤在端、側墻部位的垂向位移隨著裝貨高度的增加而逐漸減小，且呈非線性遞減。同一裝貨高度下，側墻垂向位移大于端墻垂向位移，端側墻連接處垂向位移最小。隨著裝貨高度的減小，端、側墻部位及其連接處的垂向位移差值逐漸變小，說明越靠近底部沉降逐漸變得均勻。原因是底部散粒煤所受的壓力大大超出外摩擦力，使得散體與敞車摩擦力對散體的影響逐漸減弱。

2.2 車體位移響應

散粒煤作為散粒狀介質具有流動性，其側壓力作用在車體上使車體發生位移變化，根據土力學中擋土墻側壓力理論，車體的位移變化又會反過來影響散粒煤的側壓力［13］，因此，為分析散粒煤對車體端、側墻的側壓力情況，提取計算結果中車體縱向和橫向位移響應，分別如圖5～圖6所示。

圖5 車體縱向位移響應云圖

圖6 車體橫向位移響應云圖

在散體側壓力的影響下，敞車端墻的最大縱向位移為0.028 36 mm，出現在敞車端墻頂部位置。端墻靠近底部的中間位置出現與頂部反方向的變形，這一現象的出現是由于散粒煤在重力作用下發生沉降，導致作用中心位置下移。敞車側墻的最大橫向位移為0.500 2 mm，出現在敞車側墻靠近中間位置的頂部。

3 接觸側壓力分析

以散粒煤頂部為起點，描繪散粒煤端墻中部、側墻中部測點的壓力分布曲線，并與經典庫侖理論計算結果進行對比，如圖7所示。

圖7 接觸側壓力曲線

根據土力學理論，端、側墻的位移直接影響側壓力的大小，如果端、側墻位移方向與散粒煤作用方向相同，則會出現壓力松弛現象，導致側壓力減小；如果端、側墻位移方向與散粒煤作用方向相反，則會出現壓力縮緊現象，導致側壓力增大；列車靜態工況下，端、側墻與散粒煤之間的側壓力屬于擋土墻“被動土壓力”，受散粒煤的壓力，端、側墻有向外的位移，與散粒煤作用方向相同，所以側壓力會減小。減小的程度與位移大小有關，位移大則減小的幅度越大，反之，則減小的幅度越小。

由圖7可以看出：（1）散粒煤對敞車端、側墻的側壓力沿墻高均呈非線性分布規律，且比庫侖理論計算結果略小，說明基于庫侖理論計算的車體端、側墻側壓力存在一定誤差；（2）散粒煤在車體頂點處的側壓力不為零，約為0.14 k Pa；（3）在墻高的中上部分，端墻上的側壓力值要大于側墻上的側壓力值，原因是在側壓力的作用下車體側墻頂部相對于端墻頂部發生了更大變形。底部附近，側墻上的側壓力值更大，原因是底部位置端墻變形相對更大；（4）在墻高的中部區域，近似呈線性分布，側壓力隨著深度的增加而增大；在墻高的下部分，仿真的結果與庫侖理論計算的結果迥異，側壓力值出現壓力松弛的現象。

為進一步分析同一高度散粒煤對敞車端、側墻的壓力分布規律，沿端墻—側墻水平方向選取等間距測點，描繪等高度側壓力曲線，如圖8所示。

由圖8可知，散粒煤對敞車的側壓力沿車長和車寬方向非均勻分布，且呈非線性分布。對于最為關注的車體端墻，側壓力沿車高呈非線性分布，且在頂部位置不為零；在墻高的中部區域，近似呈線性分布，側壓力隨著深度的增加而增大；在底部出現壓力松弛現象（如圖5～圖6所示），最大側壓力出現在車體底部偏上位置。

圖8 等高度接觸側壓力分布曲線

4 結 論

（1）簡化C80B型敞車模型，提出采用修正的D－P模型描述散粒煤的本構模型，考慮車體與散粒煤之間的接觸關系，實現了散粒煤對敞車車體側壓力的三維仿真模擬。該方法可以為進一步研究其他載重車型提供參考。（2）在重力作用下散粒煤發生不均勻沉降，中部沉降量最大，沿墻高沉降量呈非線性分布。敞車端墻的最大縱向位移出現在敞車端墻頂部位置；側墻的最大橫向位移出現在敞車側墻靠近中部位置的頂部。（3）通過對比分析端墻與側墻的側壓力分布曲線發現，兩者的側壓力值大小并不相同，在墻高中上部分，端墻上的側壓力值要大于側墻上的側壓力值；底部附近，

側墻上的側壓力值更大。因此，在對車體側壓力校核時，應分別校核端、側墻側壓力。（4）散粒煤對敞車的側壓力沿車長和車寬方向均呈非線性、不均勻分布，說明采用二維模型得到的側壓力分布結果不準確。

［1］ AAR Manual and Standards［S］.America：Association of American Railoads，1999.

［2］ TB／T 1335－1996鐵道車輛強度設計及試驗鑒定規范［S］.北京：中華人民共和國鐵道部，1996.

［3］ 何華.鐵路貨車的散體貨物_流體貨物動壓力研究［D］.長沙：中南大學，2008.

［4］ 曾祥坤，田紅旗.散粒貨物對鐵路敞車端墻側壓力研究［J］.鐵道學報，2007，29（4）：32-37.

［5］ 楊愛國，張志強，楊江天.基于有限元建模的敞車輕量化設計［J］.中國鐵道科學，2007，28（3）：79-83.

［6］ 王斌杰，趙方偉，李強.散粒煤對敞車靜壓力的三維有限元模擬［J］.鐵道學報，2016，38（2）：17-22.

［7］ Vidal P，Gallego E，Guaitac M，et al.Finite element analysis under different boundary conditions of the filling of cylindrical steel silos having an eccentric hopper［J］.Journal of Constructional Steel Research，2008，（64）：480-492.

［8］ Rotter J M，Hoist F G，Ooi J Y，et a1.Silo pressures predictions using discrete-element and finite element analyses［J］.Philosophical Transaction Mathematical，Physical and Engineering Sciences，Series A，1998，356：2685-2712.

［9］ Hubner A，Teng J G，Saal H.Buckling behaviour of large steel cylinders with patterned welds［J］.International Journal of Pressure Vessels and Piping，2006，（83）：13-26.

［10］ Vidala P，Gallegob E，Guaitac M，et al.Finite element analysis under different boundary conditions of the filling of cylindrical steel silos having an eccentric hopper［J］.Journal of Constructional Steel Research，2008，64：480-492.

［11］ 朱向榮，王金昌.ABAQUS軟件中部分土模型簡介及其工程應用［J］.巖土力學，2004，25：144-148.

［12］ Juan A，Moran J M，Guerra M I，et a1.Establishing stress state of cylindrical metal silos using finite element method：comparison with ENV 1 993［J］.Thin-Walled Structures，2006，44：1192-1200.

［13］ OOI J Y，SHE K M.Finite Element Analysis of Wall Pressure in Imperfect Silos［J］.Solid Structures，1997，34（16）：2065-2072.

Static Lateral Pressure Distribution Study of Granular Cargo on Gondola Car

ZHAO Fangwei，FU Xiuqin，ZHANG Hong，ZHANG Pengpai，CONG Tao，ZHANG Guanzhen，WU Si
（Metals＆Chemistry Research Institute，China Academy of Railway Sciences，Beijing 100081，China）

In order to study the static lateral pressure distribution of granular cargo on gondola car，C80B gondola car full of granular coal is regarded as the research object.Revised D－P model is adopted to simulate the constitutive model of granular coal.Through the simplified geometric model and finite element method，3－D numerical discrete model of car body is established.Flexible-flexible contact type is set between car body and granular coal.The modified hard contact is used to simulate the contact behavior.The elastic slip deformation is introduced to simulate the tangential friction behavior.Static lateral pressure on the gondola car body is simulated.The results are compared with the Coulomb pressure theory.It shows that the granular coal settled under gravity，and central vertical displacement is largest.Along the loading height，the distribution of settlement is nonlinear.The lateral pressure distribution along wall height of gondola car is nonlinear，and the value at the top is not zero.The lateral pressure along the length and width direction of gondola car is non-uniform distribution，and distribution is nonlinear.

gondola car；granular cargo；D－P model；numerical simulation；lateral pressure

U272.2

A

10.3969／j.issn.1008－7842.2016.06.11

1008－7842（2016）06－0042－04

7—）男，助理研究員（

2016－07－15）