電推進衛星角動量卸載研究

馬雪,韓冬,湯亮

1.北京控制工程研究所,北京100190 2.空間智能控制技術重點實驗室,北京100190

電推進衛星角動量卸載研究

馬雪1,2,*,韓冬1,2,湯亮1,2

1.北京控制工程研究所,北京100190 2.空間智能控制技術重點實驗室,北京100190

電推進衛星需要在進行位置保持的同時通過將推力器的指向略微偏離質心來產生控制力矩,完成角動量卸載。針對該問題,文章在給定推力器開機位置、時長和動量輪目標卸載量的情況下,提出了正常模式和故障模式下的角動量卸載算法。通過對推力模型的簡化,得出了推力器最優偏轉方向的解析解,并對考慮推力器弧段損失和不考慮弧段損失的角動量卸載算法進行了比較。仿真結果表明,所提出的卸載算法能夠在進行位置保持的同時完成角動量卸載,為電推進衛星的在軌控制策略提供了有效解決方案。

電推進;角動量卸載;小推力控制;參數優化;位置保持控制

目前,國外已有波音601 HP和702平臺、歐洲航天局ARTEMIS衛星、Loral公司的電推力衛星平臺等諸多高軌任務,搭載電推進系統作為靜止軌道衛星的主要執行機構[1]。國內已有不少學者在地球靜止軌道轉移和離軌[2-4]、深空探測[5-6]、重力場測量衛星[7]等諸多領域,開展了與電推進控制相關的研究。對于電推進衛星,星上角動量卸載的方式與傳統的化學推進衛星存在明顯區別,需要進行深入研究。

星上角動量卸載的目的是釋放星上角動量交換執行機構(動量輪、控制力矩陀螺等)因環境干擾力矩而造成的角動量累積,以避免達到飽和狀態。常用的卸載方式有磁力矩器卸載和推力器卸載。事實上,角動量卸載算法是大部分低軌、高軌衛星上普遍應用的控制算法,在航天上并非全新的問題。近年來,對角動量卸載的研究往往集中在具有特殊結構或執行新的任務的航天器上,例如對空間站等搭載控制力矩陀螺(CMG)的大型航天器的角動量管理[8-12],或是對深空探測器的角動量卸載研究[13]。而對于電推進衛星,其推力器配置為4臺電推力器呈錐形布局,推力器較少,星上角動量卸載并非獨立進行控制,需要在進行位置保持控制點火的同時,通過略微偏轉推力器的角度產生多余的力矩,實現角動量的卸載。對此,國外文獻中的方法是將位置保持控制的點火位置、點火時長以及電推力器偏轉角度作為控制參數進行優化迭代[14-15],該方法能同時對位置保持和角動量卸載的控制量實現較為精確的求解,但需要進行反復迭代,計算量相對較大。

本文考慮到星載計算機的計算能力約束,提出了位置保持控制量和推力器偏轉角度分別求解的電推進卸載算法,損失部分位置保持和卸載精度,以降低星上卸載算法的計算量。在位置保持正常和故障模式下給定推力器開機位置、時長和動量輪目標卸載量的情況下,提出考慮推力器弧段損失和不考慮弧段損失的兩種角動量卸載簡化算法,并利用數值仿真對兩種算法進行對比、驗證。結果表明,本文提出的卸載算法能夠在進行位置保持的同時完成角動量卸載,計算量大幅下降。

1 基于電推進的角動量卸載

1.1 電推進衛星位置保持點火策略

電推進衛星通常僅安裝4臺電推力器,呈錐形布局,如圖1所示。在衛星本體系下,4臺推力器成對對稱斜安裝在背地板四邊,在北側的2臺推力器為NW和NE,南側的2臺推力器為SW和SE。4臺推力器的安裝角度定義如圖2所示,α為安裝在西北向(NW)的推力器的推力方向矢量在衛星本體系x-z面投影與z軸夾角,θ為安裝在西北向(NW)的推力器的推力方向矢量在衛星本體系y-z面投影與y軸夾角,其他3臺推力器的定義與推力器NW對稱。

圖1 電推進衛星推力器布局Fig.1 Mounting position of electric thruster

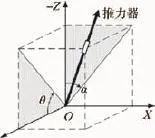
圖2 電推力器安裝角度Fig.2 Definition of gimbal angle of electric thruster

受到推力器的配置約束,電推進衛星的角動量卸載與位置保持控制之間存在耦合。電推力器在進行位置保持控制時根據卸載的方向和大小對推力方向進行略微偏轉,通過產生額外的力矩實現角動量的卸載。由此可見,電推進衛星每軌進行角動量卸載的時刻和時長與位置保持控制緊密相關。為此,本節將對電推進衛星的位置保持點火方式進行粗略介紹。

電推進衛星的位置保持以數周為一個控制周期周而復始進行。每個控制周期的前幾日由地面進行測定軌并制定位置保持策略,在此期間衛星不進行位保和卸載控制,而在剩余的時間內衛星每軌都進行數次的位置保持點火控制,并在此基礎上進行角動量卸載。電推進位置保持的點火策略有兩種形式,分別為正常模式下的位置保持策略和故障模式下的位置保持策略。正常模式即為4臺電推力器均能開機工作的模式,采取一軌分為相隔180°的2個開機時段(通常在升、降交點附近),每個時段各有2臺推力器相繼開機,利用4臺推力器控制量的排列組合實現傾角、偏心率和平經度控制,如圖3所示;故障模式下,一臺推力器發生故障,此時,僅利用未發生故障的2臺對角線上的推力器進行控制,南、北的2臺推力器除了在降、升交點附近開機外,在一個軌道周期內的第3臺位置兩臺對角線推力器相繼開機,實現位置保持控制,如圖4所示。

圖3 正常模式位置保持示意Fig.3 Station-keeping control of Nominal mode

圖4 故障模式位置保持示意Fig.4 Station-keeping control of failure mode

1.2 角動量卸載算法

當考慮位置保持控制和角動量卸載,對推力器點火時長、位置和推力器卸載偏轉角度同時求解需要進行迭代優化,計算量較大,不利于星上求解。為此,考慮到用于卸載的偏轉角度不大,對位置保持控制的影響有限,本文采取將位置保持點火時長、位置和推力器偏轉角度分開計算的方式,先求出位置保持點火位置、時長參數,再由已知的位保參數求得角動量卸載所需的推力器偏轉最優角度的解析解,降低計算量。在推力器卸載能力足夠大時,不因卸載需要改變電推力器點火時長、位置。

受到電推進衛星錐形推力器布局的影響,至少需要通過任意兩臺對角線上推力器執行卸載任務,才能對所有方向上的角動量實現較好的覆蓋。為減少推力器的轉動次數,提高驅動機構壽命,在一個軌道周期內,采用兩個對角線上推力器僅分別在一個點火位置偏移推力方向的策略,并選取推力器方向轉動方差最小的對角線推力器對進行卸載。

(1)考慮弧段損失的正常模式角動量卸載

在正常模式位置保持點火策略下,以SW和NE為例,推導角動量卸載時推力器調節角度的計算步驟。NW和SE組合的推導過程與SW和NE一致。

南、北側推力器軌道系到慣性系坐標轉換矩陣為

式中:κ為由南北位置保持傾角控制產生的點火位置偏移,與季節和年份相關。

設推力器在本體系上的安裝位置為

假設推力方向改變量在x-y平面上移動,大小為dxSW、dySW、dxNE、dyNE。為對卸載的優化問題進行簡化,假設該量為小量,不改變矢量本身大小(當推力方向改變量較小時,此簡化帶來的誤差很小)。推力大小為

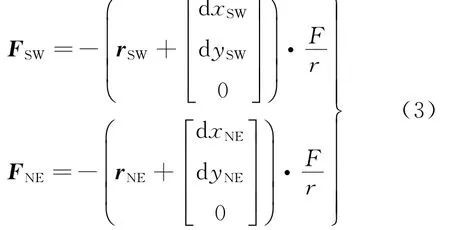
式中:F為推力大小;r為推力器距質心距離。

考慮到電推力器點火時長較長,將點火時間看成是靜止軌道衛星在軌道上運行的一個弧段,可為角動量卸載提供的動量矩公式為式中:tSW、tNE為由位置保持控制算出的單個推力器噴氣時長。

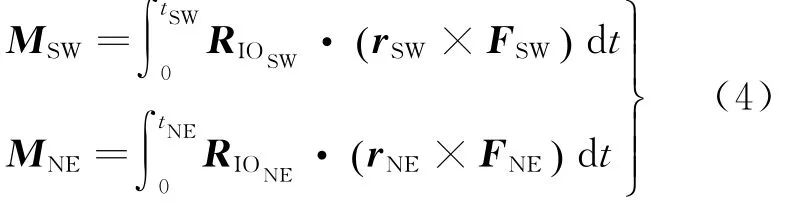
易知,角動量卸載即為求使得偏轉角方差最小的求極值問題,該問題的目標函數約束條件為

式中:Mx、My、Mz為在慣性系三個方向上的目標卸載量。

由拉格朗日乘子法,即可對該問題進行求解。設哈密頓函數極值為以下方程組的解:

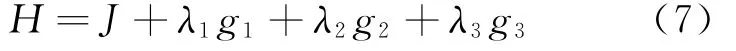
此時,待求解方程為線性方程組

依照同樣的方法,可求得另一對角線元素NW和SE的偏移量dxNW、dyNW、dxSE和dySE,并根據式(5)選擇偏轉角方差最小的一組對角線元素進行卸載。

(2)不考慮弧段損失的角動量卸載

利用上一節中的算法,雖然可求得正常模式下的角動量卸載偏轉方向,但求解過程中需要對兩個7階方陣求逆,計算量較大。因此,本節對角動量卸載算法進行簡化,進一步減小卸載算法的計算量。

不考慮弧段損失,將電推力器的點火位置看成是軌道上的一點。此時,角動量卸載提供的動量矩公式由式(4)變為

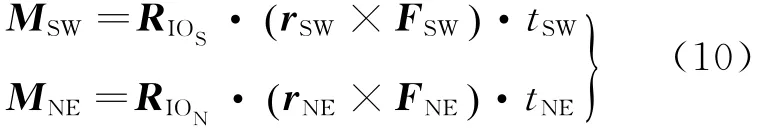
再根據式(8),可直接求出對角線上推力器的卸載偏移量:

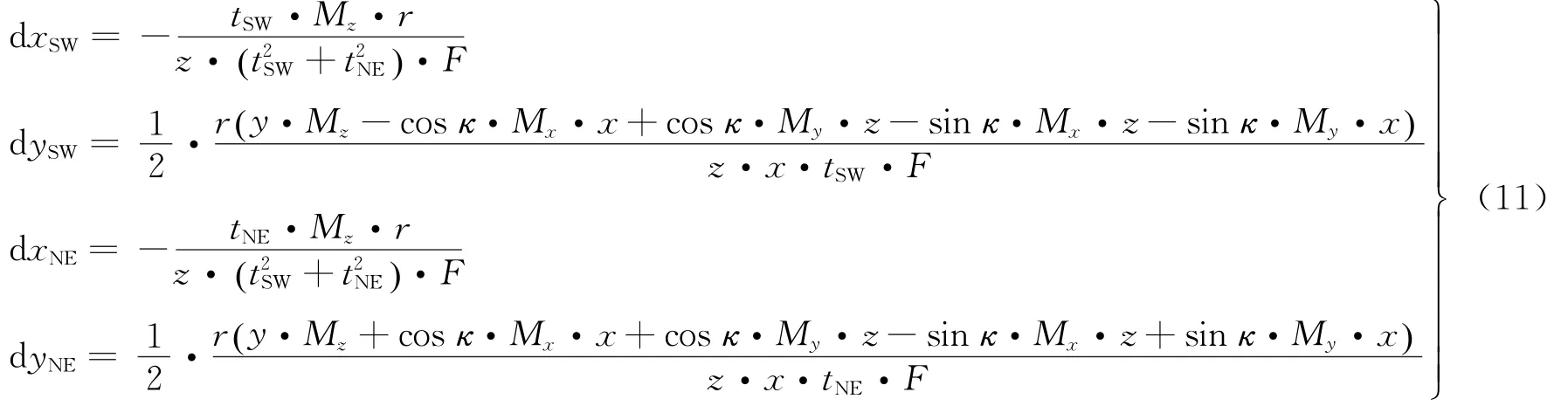
用同樣的方法,可求得另一對角線元素NW和SE的偏移量dxNW、dyNW、dxSE和dySE,在選擇偏轉角方差最小的一組對角線元素進行卸載。該方法由于不考慮弧段損失,會使卸載精度降低,但計算量大為縮小。

(3)故障模式角動量卸載

故障模式下,推力器在軌道上的三個位置點火。

三個位置上軌道系到慣性系的坐標轉換矩陣為

式中:η為故障模式下中間一次變軌所在的赤經,如圖4所示。

故障模式的角動量卸載只能依靠單一對角線上的某對推力器進行卸載,但根據選擇卸載點火段不同,有4種不同的排列組合:

其中,第4種組合M22能夠產生的角動量較小,可只考慮前3種組合,選擇偏轉角方差最小的一種組合進行卸載。

2 仿真結果

2.1 算法比較

利用上述兩種卸載算法對正常模式下位置保持時的角動量卸載進行仿真,選擇調節角度平方和較小的一對推力器完成角動量卸載,控制段每日的目標卸載量為5 N·m·s/d,方向為隨機量,分別利用考慮弧段損失和不考慮弧段損失的角動量卸載算法進行仿真驗證,仿真時間為1年,以14天為一個控制周期,14天內的前2天不進行控制,后12天進行位置保持和角動量卸載。

由于兩種算法的推力器調節角度量級相同,角度相近,僅給出不考慮弧段損失的卸載算法推力器調節角度。如圖5所示,當每日的目標卸載量為5 N·m·s/d時,推力器調節角度在5°以內。

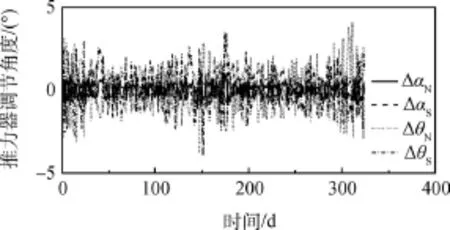
圖5 推力器調節角度曲線Fig.5 Gimbal angles of the thrusters

圖6、圖7分別為真實卸載量與目標卸載量偏差,以及真實卸載方向與目標卸載方向夾角。圖中實線為考慮弧段損失的算法偏差,虛線為不考慮弧段損失的算法偏差。如圖所示,當考慮弧段損失時,真實卸載量與目標卸載量之間的偏差在5%以內,角動量卸載方向的偏差在8°以內,具有較高的經度。當忽略弧段損失時,卸載量的偏差最大可達30%,卸載方向與目標卸載方向的夾角在15°以內,雖然在不考慮弧段損失時的情況下,卸載的精度下降,但算法依舊能夠卸載掉大部分動量輪累積的角動量。

圖6 真實卸載量與目標卸載量偏差Fig.6 Deviation of moment dumpling

圖7 真實卸載方向與目標卸載方向夾角Fig.7 Orientation deviation of moment dumpling

2.2 對位置保持的影響

本文為避免進行大計算量的優化計算,采用的是位置保持和角動量卸載分開計算的方式以求得解析解,當電推進衛星進行角動量卸載時,會將推力器方向略微偏轉,這無疑會對位置保持控制的精度產生影響。為此,本文對角動量卸載對位置保持控制的影響進行仿真驗證。對角動量卸載下的位置保持控制進行仿真,設置定點經度為東經120°,仿真時間為1年,其他仿真參數與2.1節相同。

圖8、圖9和圖10分別為考慮角動量卸載的軌道傾角、偏心率和平經度曲線,可見在疊加上卸載所需的推力器偏轉后,衛星依舊在高軌衛星位置保持控制的容許范圍之內,能夠在完成角動量卸載的同時實現位置保持控制。

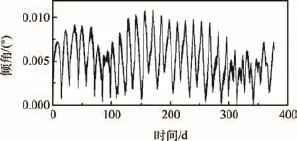
圖8 軌道傾角曲線Fig.8 Orbital inclination

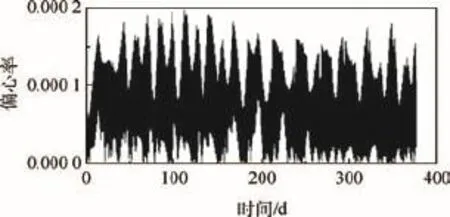
圖9 偏心率曲線Fig.9 Orbital eccentricity

圖10 平經度曲線Fig.10 Mean longitude

圖11、圖12、圖13分別為考慮角動量卸載和單純進行位置保持控制之間的控制偏差。如圖所示,角動量卸載對于南北位保的影響很小,對于東西位保的影響稍大,但也在合理的范圍內,且由于東西位保采用了反饋控制,本控制周期對位置保持產生的影響不會累加到下一個控制周期。

圖11 傾角控制偏差Fig.11 Control error of orbital inclination

圖12 偏心率控制偏差Fig.12 Control error of orbital eccentricity

圖13 平經度控制偏差Fig.13 Control error of mean longitude

3 結束語

本文提出的電推進角動量卸載方法,可用于電推進衛星進行位置保持,同時,通過偏轉電推力器的指向實現角動量執行機構(動量輪等)的角動量卸載。在給定推力器開機位置、時長和動量輪目標卸載量的前提下,推導了考慮推力器弧段損失和不考慮弧段損失的角動量卸載簡化算法,并進行了數學仿真。結果表明,考慮弧段損失的卸載精度要優于不考慮弧段損失的卸載算法,但在求解過程中需要對高維矩陣求逆,計算量明顯加大。因此,應根據星上實際計算能力選擇是否考慮弧段損失進行卸載。本文給出的角動量卸載算法能夠快速計算出卸載所需的電推力器噴氣方向,并對位置保持的控制精度影響較小,取得了較好的效果。在未來的工作中,可專門針對電推進衛星受太陽光壓力矩影響較大的特點,對電推進角動量卸載策略做進一步的研究。

References)

[1] 吳漢基,蔣遠大,張志遠.電推進技術的應用與發展趨勢[J].推進技術,2003,24(5):385-392. WU H J,JIANG Y D,ZHANG Z Y.Application and development trend of electric propulsion technology[J]. Journal of Propulsion Technology,2003,24(5):385-392 (in Chinese).

[2] 馬雪,韓冬,湯亮.電推進靜止軌道轉移與空間環境分析[J].空間控制技術與應用,2015,41(1):31-35. MA X,HAN D,TANG L.On the electricpropulsion-based geostationary transfer and space environmental analysis[J].Aerospace Control and Application,2015,41(1):31-35(in Chinese).

[3] 田百義,黃美麗,馮昊,等.GEO衛星電推進與化學推進組合變軌方案研究[J].航天器工程,2015,24(3): 28-33. TIAN B Y,HUANG M L,FENG H,et al.Orbit transfer concept for GEO satellite by combination of electric and chemical propulsion[J].Spacecraft Engineering, 2015,24(3):28-33(in Chinese).

[4] 王志剛,陳士櫓,袁建平.電推進在靜止軌道空間碎片減緩中的應用[J].飛行力學,2004,22(2):37-40. WANG Z G,CHEN S L,YUAN J P.On the application of electric propulsion in geostationary space debris mitigation[J].Flight Dynamics,2004,22(2): 37-40(in Chinese).

[5] 毛根旺,付西鵬,陳茂林.月球探測器電推進系統的應用研究[J].機械科學與技術,2008,27(7):853-856. MAO G W,FU X P,CHEN M L.Application of an electric propulsion system to a lunar detector[J]. Mechanical Science and Technology for Aerospace Engineering,2008,27(7):853-856(in Chinese).

[6] 楊福全,趙以德,李娟,等.主帶小行星采樣返回任務中的離子電推進應用方案[J].深空探測學報,2015,2(2): 168-173. YANG F Q,ZHAO Y D,LI J,et al.Application of an electric propulsion system to a lunar detector[J]. Journal of Deep Space Exploration,2015,2(2):168-173 (in Chinese).

[7] 顧左,達道安,胡長青,等.重力場測量衛星應用電推進技術[J].火箭推進,2005,31(2):23-26. GU Z,DA D A,HU C Q,et al.Application of electric propulsion technology to gravity field measurement satellites[J].Journal of Rocket Propulsion,2005,2(2): 23-26(in Chinese).

[8] 劉輝,伍斯賓斯基.利用噴氣裝置卸載航天器積累角動量的最小工質損耗控制[J].航天控制,2004,22(5): 32-35. LIU H,USPENSKY V B.Minimize propellant consumption during gyro system unloading process of spacecraft[J].Aerospace Control,2004,22(5):32-35 (in Chinese).

[9] 張軍,馬艷紅,何英姿.空間站組合體慣性系內角動量管理控制[J].空間控制技術與應用,2010,36(6):1-5. ZHANG J,MA Y H,HE Y Z.Momentum management control of space station complex in inertial reference[J].Aerospace Control and Application,2010, 36(6):1-5(in Chinese).

[10] 張志方,董文強,張錦江,等.控制力矩陀螺在天宮一號目標飛行器姿態控制上的應用[J].空間控制技術與應用,2011,37(6):52-59. ZHANG Z F,DONG W Q,ZHANG J J,et al.The application of control moment gyro in attitude control of Tiangong-1 spacecraft[J].Aerospace Control and Application,2011,37(6):52-59(in Chinese).

[11] 崔培玲,張穎.采用DGCMG的敏捷衛星姿態/角動量聯合控制[J].電光與控制,2013,20(1):49-55. CUI P L,ZHANG Y.Attitude and momentum control of agile satellite using DGCMG[J].Electronics Optics &Control,2013,20(1):49-55(in Chinese).

[12] 朱孟萍,徐世杰,陳新龍,等.基于參數辨識的大型航天器自適應角動量管理[J].空間控制技術與應用, 2014,40(3):47-52. ZHU M P,XU S J,CHEN X L,et al.Adaptive momentum management of large spacecraft based on parameter ientification[J].Aerospace Control and Application,2014,40(3):47-52(in Chinese).

[13] 戴居峰,徐紅兵,崔雁,等.“嫦娥二號"衛星L2點角動量管理[J].中國空間科學技術,2013,4(2):72-77. DAI J F,XU H B,CUI Y,et al.Momentum management of Chang’e-2 satellite on L2 point[J]. Chinese Space Science and Technology,2013,4(2): 72-77(in Chinese).

[14] ANZEL B.Method and apparatus for a satellite station keeping:US 5443231[P].1993-11-17.

[15] ANZEL B.Stationkeeping the Hughes Hs 702 satellite with a Xenon ion propulsion system[C]∥49th International Astronautical Congress.Melbourne, Australia,1998.

(編輯:高珍)

Study on moment dumpling of electric propulsion satellite

MA Xue1,2,*,HAN Dong1,2,TANG Liang1,2
1.Beijing Institute of Control Engineering,Beijing 100190,China 2.Science and Technology on Space Intelligent Control Laboratory,Beijing 100190,China

Moment dumpling of electric propulsion satellite can be established by pointing the thrust vectors slightly away from the center of mass.On the basis of this method,electric propulsion moment dumpling for both normal mode and failure mode was investigated.The analytic solution of optimal dumpling directions was given,and the question that whether the control arc should be considered was discussed.The simulation results show that proposed method can effectively perform the moment dumpling by electric thrusters.

electric propulsion;moment dumpling;low-thrust control;parameter optimization; station-keeping control

V43

:A

10.3780/j.issn.1000-758X.2016.0013

2015-11-12;

:2015-12-23;錄用日期:2016-01-18;< class="emphasis_bold">網絡出版時間

時間:2016-02-24 13:38:20

http:∥www.cnki.net/kcms/detail/11.1859.V.20160224.1338.009.html

國家自然科學基金(11502017)

*

:馬雪(1984-),女,博士,工程師,xuema.m45@gmail.com,主要研究方向為航天器動力學與控制

馬雪,韓冬,湯亮.電推進衛星角動量卸載研究[J].中國空間科學技術,2016,36(1):70-76.MA X,HAN D,

TANG L.Study on moment dumpling of electric propulsion satellite[J].Chinese Space Science and Technology,2016,36(1):70-76(in Chinese).

http:∥zgkj.cast.cn