灰色理論在廠房地坪監(jiān)測中的應(yīng)用
鄒煒
(上栗縣規(guī)劃局,江西 萍鄉(xiāng) 337009)
灰色理論在廠房地坪監(jiān)測中的應(yīng)用
鄒煒
(上栗縣規(guī)劃局,江西 萍鄉(xiāng) 337009)
依據(jù)某廠房地面監(jiān)測點數(shù)據(jù),利用灰色理論G(1.1)模型建立預測方程,對室內(nèi)地面監(jiān)測點后期的變形情況進行預測。
灰色理論;預測;GM(1.1)
【DOI】10.13616/j.cnki.gcjsysj.2016.07.029
1 引言
由于沉降監(jiān)測一般具有趨勢性的特點,所以結(jié)合一個沉降監(jiān)測資料運用等間距GM(1,1)模型進行分析,驗證等間距GM(1,1)模型具有較高的預測精度。
2 灰色系統(tǒng)理論
灰色系統(tǒng)理論是研究灰色系統(tǒng)分析、建模、預測、決策和控制的理論。并結(jié)合數(shù)學方法,發(fā)展出一套解決信息不完全系統(tǒng)(灰色系統(tǒng))的理論和方法。
2.1 灰色GM(1,1)模型
在趨勢分析常用的是GM(1,1)模型,即設(shè)系統(tǒng)的原始數(shù)據(jù)序列為 X(0)=[x(0)(1),x(0)(2),…,x(0)(n)],則 GM(1,1)模型為:式中X(1)(k)為原始數(shù)據(jù)序列的累加生成AGO,即設(shè)微分方程的系數(shù)a和參數(shù)u組成向量按最小二乘法解得方程的解為原始數(shù)據(jù)序列的預測公式為
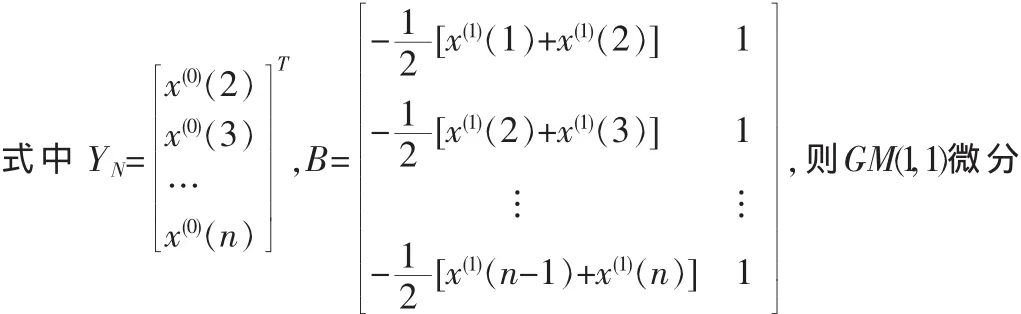
在實際的智能診斷應(yīng)用中,由GM(1,1)模型預測得到的狀態(tài)特征向量通常是作為診斷模塊判別層輸入的。
2.2 模型精度檢驗
通過檢驗的標準為精度等級越小越好,四級為不通過。精度等級如表1所示。

表1 精度等級表
3 實例分析
因上海為沖擊平原,土質(zhì)非常松軟,廠房為獨立基礎(chǔ),在廠房室內(nèi)地面設(shè)置橫縱格網(wǎng),格網(wǎng)點為監(jiān)測點,對監(jiān)測點進行定期監(jiān)測,監(jiān)測周期為每月一次。現(xiàn)將某部分監(jiān)測數(shù)據(jù)表如表2所示。
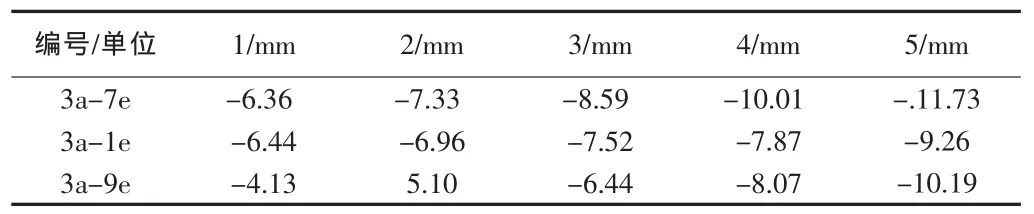
表2 部分監(jiān)測數(shù)據(jù)
3.1 建立預測模型
已現(xiàn)場監(jiān)測數(shù)據(jù)為基礎(chǔ),利用灰色理論
X(1)(5)=(-6.36,-13.69,-22.28,-32.29,-44.02)系數(shù)a和參數(shù)u組成向量a贊=[a,u]T=[-0.1560,-5.7690]T
所以預測方程為x贊(1)(k+1)=-43.32725032e0.156059k+36.9672503
3.2 預測模型擬合誤差分析
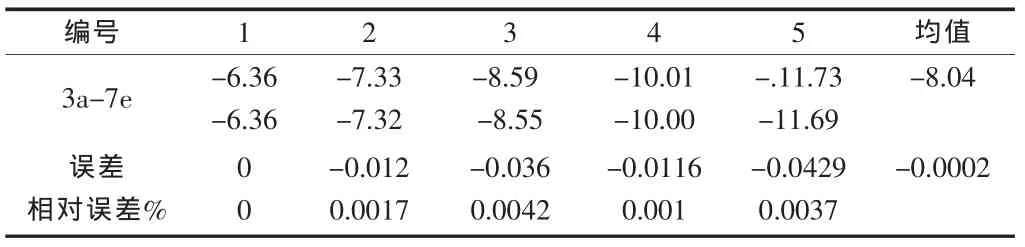
表3 預測模型擬合誤差分析表
4 結(jié)束語
1)根據(jù)室內(nèi)地的監(jiān)測數(shù)據(jù)通過GM(1.1)模型方法,得出精度為一級,所以該數(shù)據(jù)適合灰色理論模型,可以推廣應(yīng)用。
2)通過室內(nèi)地的監(jiān)測預測數(shù)據(jù)可以得出,灰色GM(1.1)只適合預測后幾期的數(shù)據(jù)。所以在選擇數(shù)據(jù)時,應(yīng)該注意原始數(shù)據(jù)和預測后期數(shù)據(jù)的比重,這樣預測精度會高些。
【1】黃聲享,李志成.工程建筑沉降觀測的非等間距灰色建模[J].地理空間信息,2004,2(1):41-43.
【2】趙顯富,郭淳.灰色預測模型及其在沉降預測中的應(yīng)用[J].鐵路航測,2002(3):30-32.
【3】羅旭,胡曉民,高學斌.灰色理論在沉降監(jiān)測信息系統(tǒng)中的應(yīng)用[J].工業(yè)建筑,2006(S1):662-664.
Application of Grey Theory in the Workshop Floor Monitoring
ZOUWei
(ShangliCountyPlanningBureau,Pingxiang337009,China)
Based on a certainworkshop groundmonitoringdata, usingthe theoryof greyG(1.1)model to establish prediction equation to predict the deflection ofthelateindoorgroundmonitoringstations.
greytheory;predict;GM(1.1)
TV698.1
A
1007-9467(2016)07-0047-02
2016-6-27
鄒煒(1986~),男,江西上栗人,助理工程師,從事房屋測繪研究,(電子信箱)441246552@qq.com。

