BDS與GPS三頻模糊度解性能分析
劉禮衡,滿小三,葉險峰
(1.湖南省第一測繪院,湖南 衡陽 421001;2.解放軍信息工程大學,鄭州 450001;3.湘潭大學能源工程學院,湖南 湘潭 411100)
BDS與GPS三頻模糊度解性能分析
劉禮衡1,滿小三2,葉險峰3
(1.湖南省第一測繪院,湖南 衡陽 421001;2.解放軍信息工程大學,鄭州 450001;3.湘潭大學能源工程學院,湖南 湘潭 411100)
隨著BDS與GPS都已經播發三個頻率,采用無幾何無電離層模糊度解算方法,著重分析了BDS與GPS三頻模糊度解算性能。通過二組BDS/GPS實測三頻基線數據分析表明:BDS的載波相位多路徑延遲比GPS更為嚴重,致使短基線BDS窄巷模糊度通過多個歷元平滑無法收斂為正確值,而GPS可以通過多個歷元可以平滑的收斂為正確值。
無幾何無電離層;BDS;窄巷模糊度
【DOI】10.13616/j.cnki.gcjsysj.2016.07.145
1 引言
高精度GNSS定位的前提條件是正確的固定模糊度值。隨著GPS現代化及我國北斗衛星導航系統逐步由區域衛星導航系統發展為全球衛星導航系統,且都播發3個頻率的導航信號,頻率的多樣性可以提高無幾何模糊度解算方法的可靠性[1]。
在三頻情形下,一般采用TCAR算法解算模糊度,但是該算法的第二步和第三步很容易受到雙差電離層殘差的影響,尤其是第三步要求雙差電離層殘差在cm級,才能保證窄巷模糊度固定成功。即使在短基線的情況下,雙差電離層殘差也很容易到達cm級。由此可見,雙差電離層殘差是影響TCAR算法中寬巷及窄巷模糊度解算的關鍵因素。為提高模糊度固定成功率,必須要消除或減弱雙差電離層殘差的影響。一般對窄巷模糊度采用無幾何無電離層模型[2],通過多歷元平滑獲取正確的窄巷模糊度值。許多學者對三頻模糊度解算的研究都是采用仿真數據,沒有考慮實際情況的復雜性,比如載波相位多路徑延遲。
文章通過實測數據分析了采用無幾何無電離層模糊度解算的BDS與GPS模糊度的收斂時間及模糊度的收斂值,初步評估了BDS與GPS三頻模糊度的解算性能。
2 無幾何無電離層模糊度解算
幾何無關(Geometry-free)模型是指采用多頻偽距和相位組合觀測值消除幾何誤差的模糊度求解模型,考慮幾何無關模型中電離層延遲的影響[3~5],幾何無關模型可以表示為:
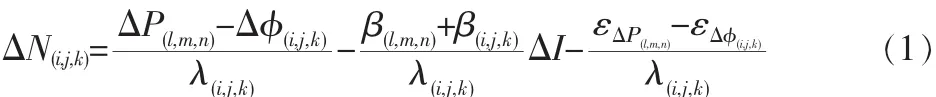
式中,△P為雙差偽距組合觀測值;△準為雙差載波相位組合觀測值;△I為L1頻點上的一階雙差電離層殘差;β為相對于f1的一階電離層延遲放大系數;ε為組合觀測值的雙差噪聲;λ為組合觀測值波長;△N為組合觀測值雙差模糊度;l,m,n,i,j,k為組合觀測值的整數系數。
顯然,采用幾何無關模型求解模糊度的主要限制是電離層延遲和偽距噪聲。
假定不同頻率的雙差載波相位觀測值精度相等,且為:

由于BDSB3頻點的碼率是B1和B2頻點的10倍,因此B3頻點的偽距觀測值精度優于B1和B2頻點的偽距觀測值[6]。則不同頻點的雙差偽距觀測值精度可以表示為:

式中,n=1,2,…,10。
根據誤差傳播率可知,雙差模糊度的精度為σ△N(以周為單位):
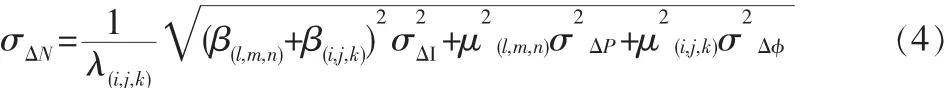
根據多頻線性組合觀測值理論,篩選的超寬巷(EWL)、寬巷(WL)和窄巷(NL)載波相位觀測值分別為:準(0,1,-1)、準(1,-1,0)和準(0,0,1)。
首先,固定超寬巷模糊度(EWL):
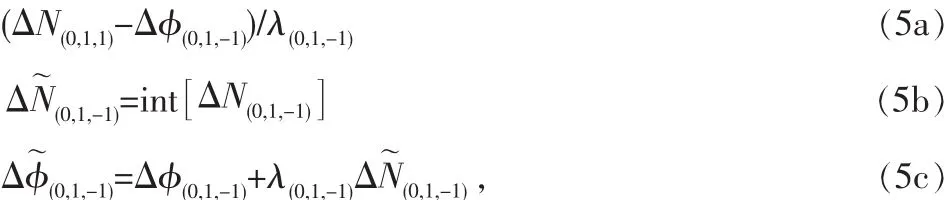
式中,int[·]表示四舍五入取整。其次,固定寬巷模糊度(WL):

最后,固定窄巷模糊度(NL):
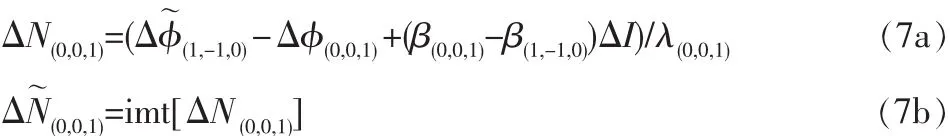
對于傳統的TCAR而言,窄巷模糊度由于其波長較短,易受雙差電離層殘差的影響。由于窄巷模糊度浮點解服從正態分布,其標準差可根據公式(4)求取,根據相關文獻可求取窄巷模糊度的固定成功率[7]。當雙差電離層殘差大于7cm時,窄巷模糊度固定成功率幾乎為0(見圖1)。故可以考慮采用無幾何無電離層模型,無幾何無電離層模糊度解算的前兩步與傳統的TCAR沒有差別,主要在于第三步窄巷模糊度的固定差別,無幾何無電離層模糊度解算窄巷模糊度的固定可以表示為:
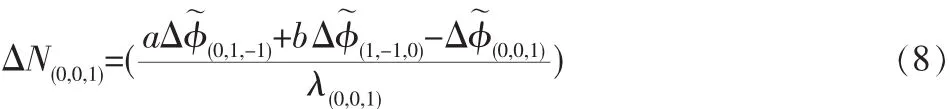
為了消除或減弱對流層誤差、雙差電離層殘差、軌道誤差等誤差,組合系數a,必須滿足以下條件:

此時,窄巷模糊度的觀測噪聲被放大,但是由于觀測噪聲服從零均值正態分布,故可以通過多個歷元平滑,然后取整獲取正確的窄巷模糊度值。


圖1 雙差電離層殘差對單歷元寬巷NL模糊度固定成功率的影響(σ△準=4mm,σ△P=60cm)
3 算例分析
文章采用TRIMBLENETR9型接收機采集了2組BDS/GPS三頻基線實測數據,基線數據A與B共用一個基站。數據的概況見表1。為了更好地分析BDS與GPS三頻模糊度解算的性能,統計了超寬巷、寬巷單歷元模糊度固定成功率及窄巷模糊度的收斂速度和收斂值。試驗中,設置截止高度角為25o,消除或減弱多路徑的影響,并且考慮了不同參考衛星的影響。通過采用LAMBDA方法多歷元連續搜索[8],確定正確的模糊度值作為無幾何無電離層模糊度解算的參考值。
從表2可以看出,以GEO衛星C01衛星為參考衛星,對數據A(零基線)、B(短基線),所有衛星對的超寬巷單歷元模糊度固定成功率總是100%,數據A和數據B的寬巷單歷元模糊度的成功率也超過99.99%。故BDS衛星超寬巷、寬巷模糊度可以實現單歷元模糊度固定或者通過幾個歷元即可以平滑收斂到正確的模糊度值。以IGSO衛星為參考衛星,可以得到以GEO為參考衛星同樣的結論(限于篇幅,未列出)。

表1 數據概況
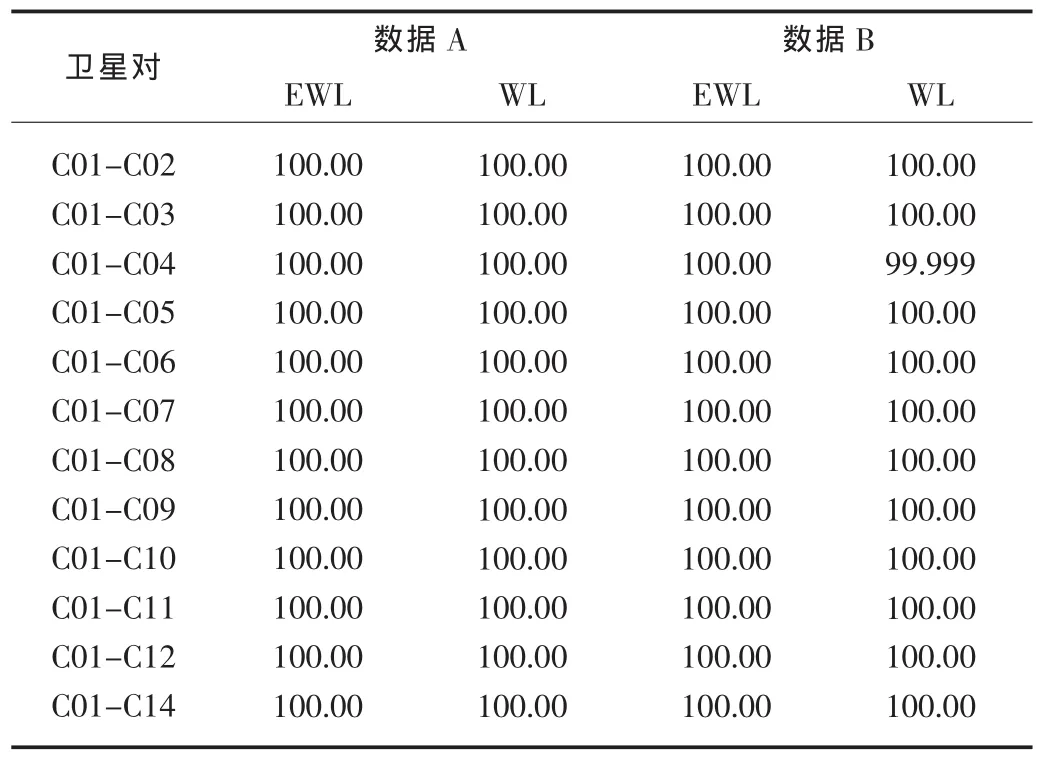
表2 數據A和BBDS衛星對超寬巷、寬巷單歷元模糊度固定成功率

圖2 數據A與數據B一天之內的GPS衛星跟蹤情況,藍色線條表示播發L5信號的衛星
從圖2可以看出,數據A和數據B在截止高度角為5o時,一天之中可以觀測到播發L5導航信號的衛星總共為8顆,但是在同一時段最多可以觀測到6顆,最少僅為2顆。為了分析每顆播發L5信號的衛星,因此,可以以每3h為一段進行分析處理。分段分析衛星具體情況見表3。
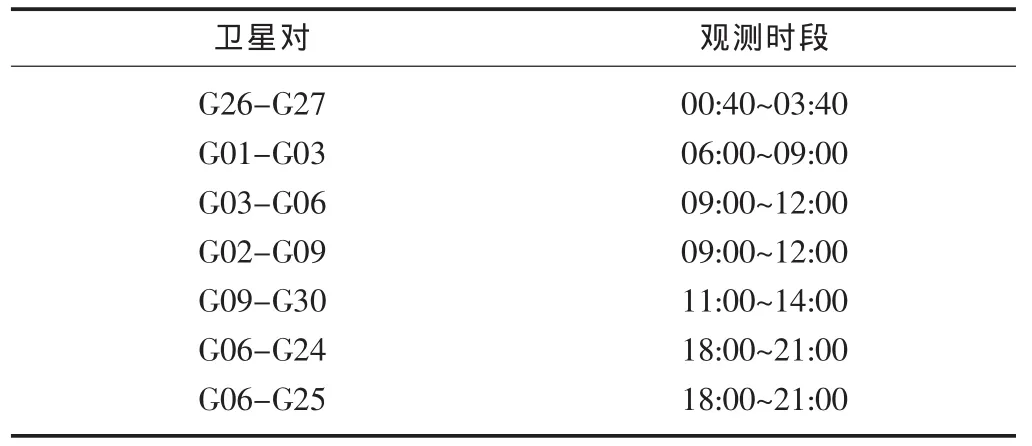
表3 數據A和B不同時段的GPS衛星對
從表4可以看出,對數據A(零基線)、B(短基線),所有GPS衛星對的超寬巷及寬巷模糊度固定成功率總是保持99.999%以上。故GPS衛星對的超寬巷及寬巷也可以實現單歷元模糊度快速固定。結合表2,可以得出:BDS與GPS采用無幾何無電離層模糊度解算的超寬巷及寬巷可以實現單歷元模糊度解算或幾個歷元平滑收斂為正確值。
從表5可以看出,對于數據A,數據處理時的截止高度角僅為25°,以C01-C02為代表,其窄巷模糊度通過幾個歷元可快速地收斂為正確值。根據表3的GPS衛星對的窄巷模糊度同樣地可通過幾個歷元快速地收斂為正確值,在GPS數據處理時,截止高度角為5°,以便處理更多的歷元數據。圖3、圖4描繪了數據A的BDS與GPS窄巷模糊度誤差及收斂的時間序列 (限于篇幅,BDS以C01-C02為代表;GPS以G06-G24為代表)。

表5 數據ABDS衛星對不同歷元數收斂的窄巷模糊度值
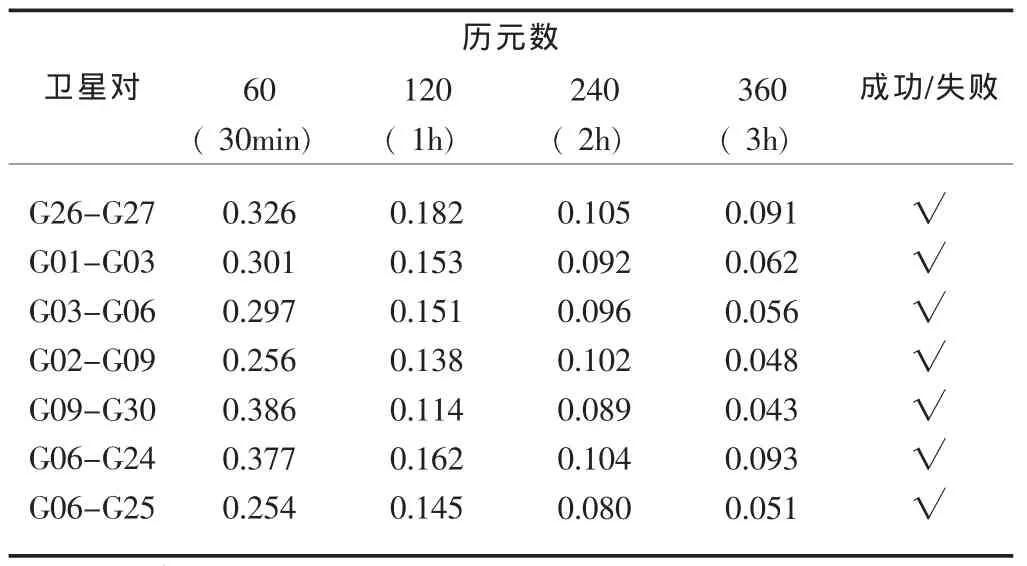
表6 數據AGPS衛星對不同歷元數收斂的窄巷模糊度值
從圖5可以看出,對于數據B,數據處理時的截止高度角僅為25°,以C01-C02衛星對為代表,其窄巷模糊度通過整個歷元平滑也沒有收斂為正確值。且出現了有周期性的波動情況,一個周期大概6h。這一現象可能是由載波相位多路徑引起,可見載波相位多路徑嚴重影響著窄巷模糊度的固定。以C06為參考衛星,也有類似的情況(限于篇幅,未繪出相應的圖)。然而,根據表6的GPS衛星對所以窄巷模糊度可以通過多個歷元平滑收斂為正確的模糊度值,數據處理時的截止高度角僅為5°,以便處理更多的歷元數據(限于篇幅,僅繪出以G06-G24為代表的窄巷模糊度誤差圖),見圖6。
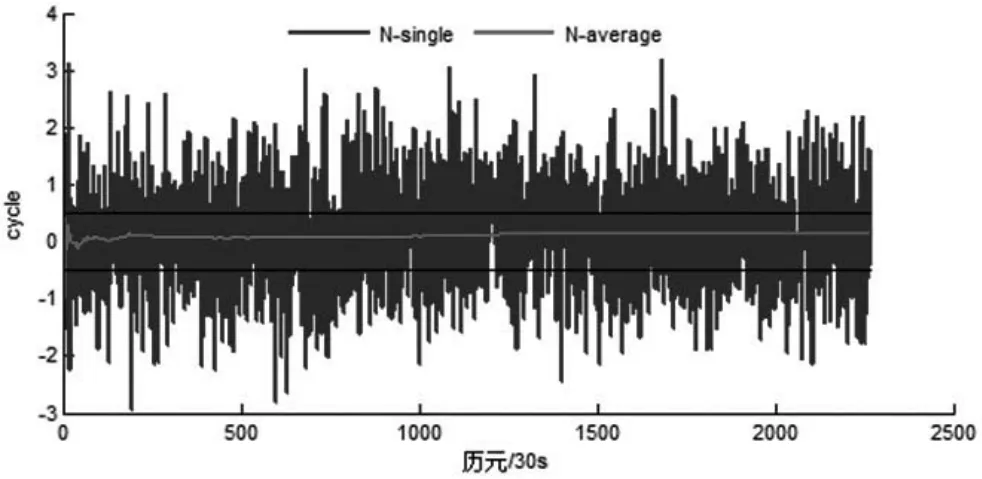
圖3 數據ABDSC01-C02衛星對窄巷模糊度誤差及其收斂的時間序列
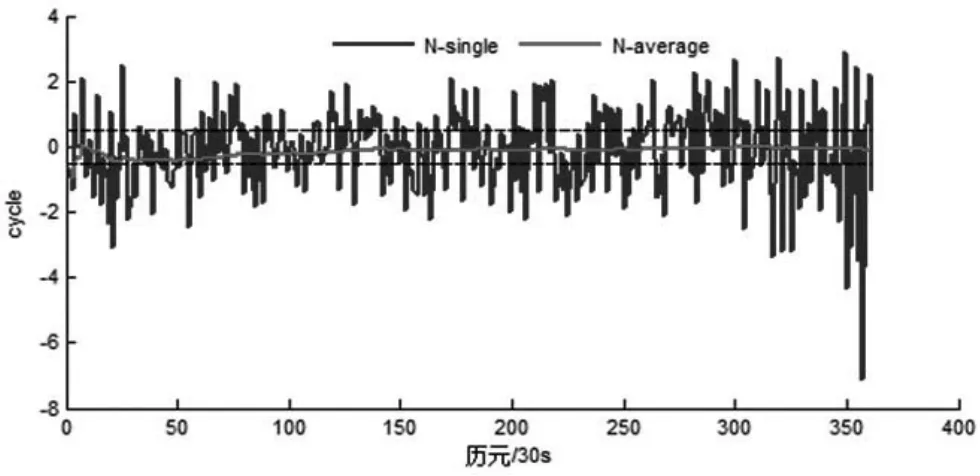
圖4 數據AGPSG06-G24衛星對窄巷模糊度誤差及其收斂的時間序列
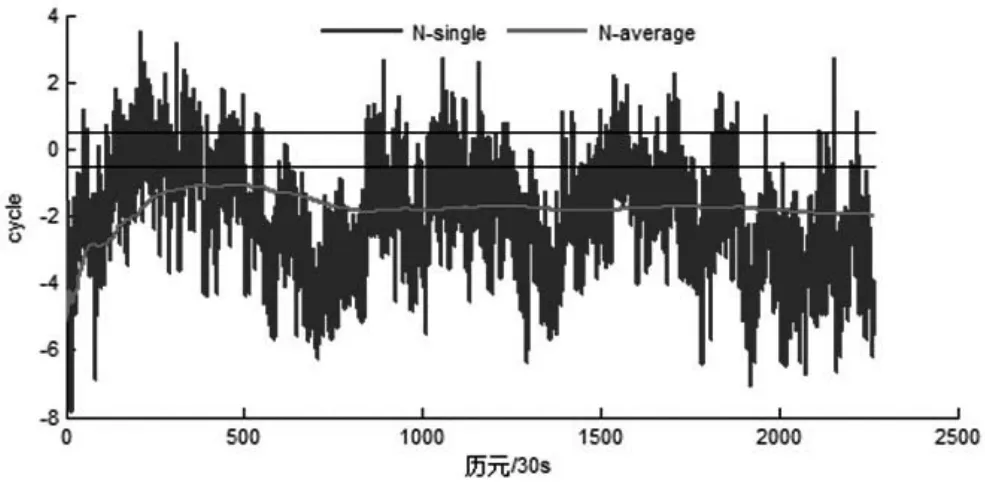
圖5 數據BBDSC01-C02衛星對窄巷模糊度誤差及其收斂的時間序列
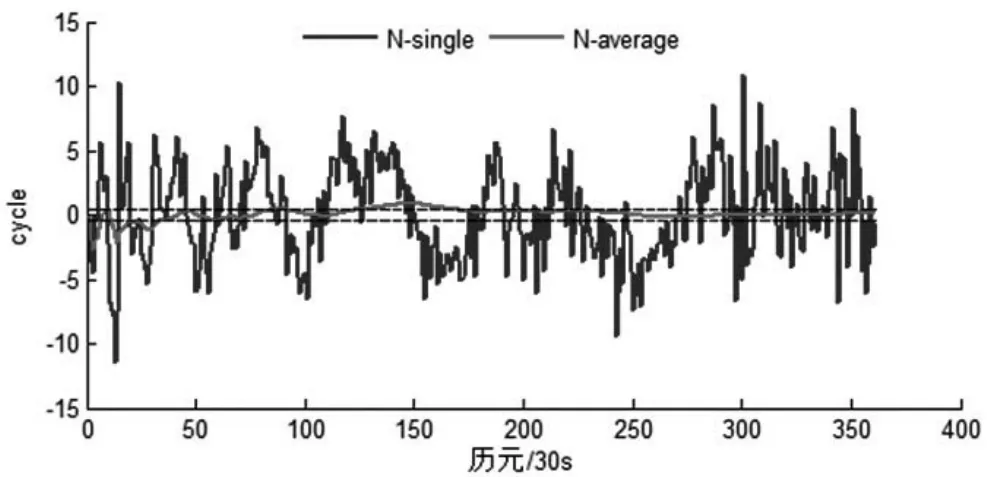
圖6 數據BGPSG06-G24衛星對窄巷模糊度誤差及其收斂的時間序列
4 結論
文章采用的無幾何無電離層模糊度解算方法,消除或減弱了對流層延遲、軌道誤差及電離層延遲的影響,僅剩觀測噪聲及多路徑的影響。通過二組實測數據對BDS與GPS的三頻模糊度解算性能進行評估分析,可以得出以下結論:(1)對于超寬巷及寬巷模糊度,BDS與GPS都能夠實現快速地固定,模糊度解算性能相當,不受基線長度的影響;(2)由于BDS的載波相位多路徑比GPS很嚴重,其窄巷模糊度通過多歷元平滑無法收斂為正確值,而GPS可以通過多個歷元可平滑收斂為正確值。
【1】李金龍.BDS/GPS多頻實時精密定位理論與算法[D].解放軍信息工程大學,2014.
【2】LiB,FengY,ShenY.Threecarrierambiguityresolution:distanceindependentperformancedemonstratedusingsemi-generatedtriple frequencyGPSsignals[J].GPSSolut,2010,14(2):177-184.
【3】FengY.GNSSthreecarrierambiguityresolutionusingionosphere-reduced virtualsignals[J].JGeod,2008,82(12):847-862.
【4】李博峰.混合整數GNSS模型參數估計理論與方法[M].北京:測繪出版社,2014.
【5】Wangk,Rothacher.M.AmbiguityResolutionfortriple-frequencygeometryfreeandionosphere-freecombinationtestedwithrealdata[J].JGeod,2013, 87:539-553.
【6】TangW,DengCetal.Triple-frequencycarrierambiguityresolutionfor Beidounavigationsatellitesystem[J].GPSSolut,2013,18(3):335-344.
【7】TeunissenP.J.G.SuccessProbabilityofIntegerGPSAmbiguityRounding andBootstrapping[J].JournalofGeod,1998,72:606-612.
【8】Teunissen,P.J.L.Theleastsquaresambiguitydecorrelationadjustment:a methodforfastGPSintegerambiguityestimatio[J]n.JournalofGeod,1995, 70:65-82.
Performance Analysis of BDS and GPS Triple-frequency Ambiguity Resolution
LIULi-heng1,MANXiao-san2,YEXian-feng3
(1.TheFirstSurveyingandMappingInstituteofHunanProvince,HengYang421001,China; 2.ThePLAInformationEngineeringUniversity.Zhengzhou450001,China; 3.SchoolofEnergyEngineering,XiangtanUniversity,Xiangtan411100,China)
AsBDSandGPShave been broadcast triple-frequency, adopting geometry-free and ionosphere-free ambiguityresolution, this paper emphatically analyzesthe performance ofBDSandGPStriple-frequencyambiguityresolution.The two group ofBDS/GPS triple-frequencybaseline real data shows that the carrierphasemulti-pathdelayofBDSisseriousthanGPSasa result, the narrowlane ambiguityofBDScan't converge to correct valuesbymultiple epoch ,but the GPScan convergetothecorrectvaluebymultipleepoch.
geometry-freeandionosphere-free;BDS;narrowlaneambiguity
P2
A
1007-9467(2016)07-0230-04
2016-6-21
劉禮衡(1974~),男,湖南耒陽人,2008年評為測繪工程師,從事測繪數據處理研究,(電子信箱)hnliuliheng@163.com。

