基于OpenGL生成TI N的程序研究
■閔盛彪 寇攀
(四川省林業科學研究院 四川 成都610081)
基于OpenGL生成TI N的程序研究
■閔盛彪 寇攀
(四川省林業科學研究院 四川 成都610081)
TIN可以用來實現復雜物體表面的逼近以及地形起伏變化的模擬,在三維可視化和地理信息系統中得到了廣泛的應用。本文主要介紹了TIN、TIN的生成算法以及離散點凸包的生成,同時以VC++6.0為平臺,調用OpenGL庫函數實現了TIN網的繪制和TIN形成區域的繪制,最后通過導入不同的實驗數據以驗證本文所述方法的可行性。
TIN;凸包;VC++6.0;OpenGL;地形模擬
0 引言
在現實世界里,地球表面呈現出的是一種不規則連續變化的曲面,為此我們在對地球表面進行模擬時,只能利用一系列的微小曲面,通過逼近的方法來實現仿真顯示。利用數字高程模型(DEM)對地球表面地形做數字描述和模擬可以很好的解決從現實物體到計算機的模數轉化,因此在測繪工程,三維可視化,虛擬現實等領域中得到了廣泛的應用。DEM有三種主要的表示模型:規則格網模型,等高線模型和不規則三角網。規則網格模型GRID,只適用于地形平坦的地方,存在大量的數據冗余,且在不改變網格大小的情況下很難表達復雜多變的地物。而不規則三角網TIN在減少數據冗余的同時能夠根據地形起伏變化來改變采樣點的密度和位置,使得表面建模更為方便靈活。利用TIN不但便于空間分析中的計算,而且還能按地形特征點如山脊,山谷線,地形變化線等來表示數字高程等特征,與GRID相比,更能表現地形細節[1]。
VC是一門功能強大易于理解和掌握的計算及編程語言,而OpenGL是一個定義了跨語言、跨平臺的編程接口的規格,是一個專業的圖形程序接口,其多功能且便于調用的底層圖形庫是整個技術的主要支撐。本文主要介紹的就是利用三角網生成算法生成TIN并調用OpenGL庫函數在VC6.0環境下的實現繪制的過程。
1 TIN生成算法及其特點
1.1 Delaunay三角網法則
一個任意的三角剖分并非是理想的三角剖分,利用隨機分布的離散高程采樣點建立連續覆蓋整個區域的TIN的技術關鍵就是確定哪三個點可以構成一個最佳三角形,并使得每個離散采樣點均為三角形的頂點。通常構建的三角網并沒有考慮到地性線(山脊線、山谷線)的框架作用,而一些地區存在大面積水域等內部不需要構網的區域,因此要對三角網的構建進行約束。Delaunay三角形具有良好的特性,利用它可以在垂直投影的地面點中根據實際情況構造最佳三角形,該方法應當滿足如下的法則:Delaunay三角網為相互鄰接且互不重疊的三角形的集合,每一個三角形的外接圓內不包含其他點。Delaunay三角網由對應Voronoi多邊形的點連接而成。Delaunay三角形有三個相鄰點連接而成,這三個相鄰頂點對應的Voronoi多邊形有一個公共的頂點,此頂點是Delaunay三角形外接圓的圓心。
根據Delaunay三角網的實現過程的不同,可以分為逐點插入法、分治算法、凸包算法、三角網生長算法等。本文主要討論了三角網生長算法,并用該算法實現TIN的繪制。
1.2 三角網生長算法
三角網生長算法的基本思路是:首先找出離散點集中相距最短的兩點,連線成為TIN的初始基線;然后按D-TIN的判斷方法找出包含此基線的Delaunay三角形的第三個端點,該端點應該位于基線的右側;連接新點與原來的兩點形成兩條新邊;再按D-TIN的判斷方法找出包含此兩邊的另外兩個Delaunay三角形的第3端點;依此循環處理所有的新生成的邊,直到所有的離散點均為D-TIN的端點。例如在離散數據中任意選擇一點A作為第一個三角形的第一個端點,然后尋找距離其最近的一點B作為第二個頂點,對AB附近的點C計算其余弦值,如果最小則C為第三個頂點。尋找C點關于AB異側的點,在所有的備選點中,按照角度最大原則選擇一點D作為AB邊上新生成三角形的第三個頂點。同理對所有的三角形進行擴展,直到所有的點被添入到不規則三角網中。
2 離散點的凸包生成
2.1 最小二維凸包
最小凸包計算在地理信息系統中有著廣泛的應用,如進行區域裁剪,獲得數字地面模型等空間分析模型的有效計算區域等。在本次程序設計中,生成離散點的凸包主要是為了繪制出TIN的區域邊界。在給定平面上的一個點集中找出一個最小點集順次連結形成一個凸多邊形,使得點集中的點皆在此多邊形內或此多邊形上,這個凸多邊形就是給定點集的最小二維凸包。
2.2 卷包裹算法
經過長期的研究,計算機科學家們推出了一系列的凸包生成算法,比較著名的有Graham掃描算法、快速凸包算法以及卷包裹算法等。在此我們探究通過卷包裹算法,來實現最小二維凸包的尋找。
卷包裹算法是凸包問題的最直觀的一種解法,它是Chand和Kapur于1970年提出的,其基本思想如下:首先過y坐標最小的點p1,畫一水平直線AB,顯然該點是凸包的一個頂點。然后AB繞p1按逆時針方向旋轉,碰到S中的第二個點p2時,直線AB改繞p2按逆時針方向旋轉而在p1與p2之間留下一條線段,該線段為凸包的一條邊。繼續旋轉下去,最后直線AB旋轉360°回到p1,便得到所要求的凸包。直線AB繞點pi的旋轉是通過如下方法實現的:首先連接pi與非凸頂點pj得到線段pipj,然后求這些線段與AB與pipj的夾角,組成最小夾角的另一端點pi+1即凸包頂點。
3 TIN的程序設計及實現
3.1 數據結構
在程序實現TIN的繪制過程中,首先要針對不規則三角網自身的特點進行數據結構的設計,在此主要的數據結構有記錄離散數據的點數據結構,記錄邊信息的線數據結構,存儲三角形的三角形數據結構,以及在凸包形成過程中所使用到的節點數據結構等。
(1)離散點數據結構。程序中使用vector
(2)線數據結構。主要記錄三角形邊兩端點的坐標信息,用數組vector
struct Line//儲存直線的兩個端點
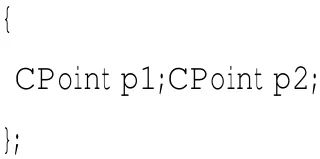
(3)三角形數據結構。vector

(4)在所有離散點的凸包的形成過程中,根據算法的要求不但要記錄位于凸包線上點的坐標而且還要記錄該點與下點連線與旋轉線的夾角,使用數組vector

3.2 程序的實現
3.2.1 數據的讀取和顯示
考慮到在實際中用來構成TIN的離散點數據量比較大,因此在該程序中數據是以*.TXT文件的形式存儲于硬盤上,當程序運行時,通過調用CstdioFile類構建的對象,對文件進行操作,并通過函數WriteString()逐行將數據讀取到內存中。在狀態欄中分別顯示了讀取點的個數以及在構網之后形成三角形的個數,該功能可以通過構建CstatusBar類對象來實現。
3.2.2 TIN的繪制
根據算法,TIN的生成可以分為這樣幾步,首先確定基線從右邊開始找點,然后調用函數GetThirdPoint(CPoint p1,CPoint p2)找到第三個點形成三角形,并將其存儲到數組vector


3.2.3 繪制離散點的凸包
根據卷包裹算法,在求離散數據凸包上點的時候需要用數據結構Node來記錄當前點坐標以及與下點連線同旋轉線之間的夾角。首先找到Y值最大的一個凸包極點做基點,然后求出所有點與旋轉線之間的夾角,快速排序找出夾角小的那一個點作為凸包點,最后轉到下一個點,以該點為基點,重復尋找,直到形成一個封閉的凸多邊形。部分代碼如下:

3.2.4 程序演示
本實驗中,以一個存有1000個離散點的文件為例,先打開文件導入數據,點擊按鈕生成TIN,再點擊按鈕繪制出TIN的生成區域,在文檔視圖的狀態欄里,可以看到當前點的個數以及生成三角形的數量。經過驗證,發現生成的TIN網滿足最大最小化原則,符合實際應用的要求,生成結果可以圖片的形式導出,如下圖所示程序研究效果。
TU195[文獻碼]A
1000-405X(2016)-12-240-3

