直流配電網潮流計算模型及算法

趙冠琨

(華北電力大學電氣與電子工程學院，北京市 102206)

直流配電網潮流計算模型及算法

趙冠琨

(華北電力大學電氣與電子工程學院，北京市 102206)

直流配電網以其傳輸容量大，適合分布式電源接入等優勢引起國內外廣泛關注，而目前其研究重點主要在結構、能效、控制、保護等方面。針對直流配電網潮流計算問題，建立考慮開關損耗及電感電容寄生參數的非理想變換器穩態模型，給出Buck，Boost等6種變換器在連續電流模式(continuous current mode，CCM)下的穩態模型參數。考慮直流配網中只有有功功率與電壓幅值，直流變換器可采用不同控制策略的特點，建立了含變換器直流配網的牛頓拉夫遜法雅克比矩陣各元素等潮流計算模型。通過對典型14節點直流配電網的算例測試，運用本文建立的模型和方法進行了潮流計算并與PSCAD仿真結果對比分析，驗證了所提模型和算法的正確性。

直流配電網; 潮流計算模型; 換流器; 牛頓拉夫遜

0 引 言

近年來，隨著經濟的快速發展，負荷需求日益增加。傳統的交流配電網面臨供電容量不足和電力線路飽和等問題，分布式電源接入交流配電網的控制策略因其間歇性和隨機性而變得復雜。相反，直流配電網具有傳輸容量大、適于分布式電源接入、無需無功補償等優點[1-7]，同時，能量轉換環節的減少使其能量傳輸效率高，上述優勢使直流配電網獲得了國內外學者的廣泛關注。

目前，直流配電網的研究工作已在全球范圍內展開，在拓撲結構、能量效率、控制和保護方面已有相關結論[8-9]。然而，直流配電網的潮流計算鮮有研究，文獻[5]提出了直流牛頓拉夫遜公式。為了解決直流配電網潮流計算問題，應考慮直流配電網的關鍵設備和參數。在直流配電網中，采用換流器而非變壓器來變換電壓等級。在換流器的建模方面，文獻[10-11]建立了整流器和逆變器的穩態數學模型。文獻[12]提出一種適用于新型直流配電網的雙向穩壓型電壓平衡器，可以實現平衡輸出端電壓波動，維持輸出端的電壓穩定。文獻[13]在連續電流模式下采用狀態空間平均法建立了DC-DC升壓變換器模型。文獻[14]提出了工作于連續電流模式下的PWM型開關轉換器模型，建立了采用受控源的升壓轉換器等效模型，其結果與采用狀態空間平均法相同。除此之外，也提及到了小信號分析法[15]和阻抗法[16]等其他方法。除了常用的方法外，文獻[17]提出了連續電流模式下基于拉普拉斯和Z變換的降壓-升壓DC-DC變換器數學建模方法。文獻[18]運用簡單的電路分析方法，得出直流變換器穩態工作時的主要電氣特性，從而根據工作特性建立了非理想Buck、Boost變換器的穩態模型。上述文獻都是針對某個特定的變換器建模，然而，由于DC-DC變換器種類眾多、結構復雜，在直流配電網潮流計算中，需要對非理想變換器的統一的穩態模型進行研究。

直流配電網是一種新型的配電模式。在直流配電網中，交流電源、分布式電源、儲能設備、交流負荷和直流負荷都通過電力變換器接于直流配電網中。 直流變壓器用于連接中壓配電網和低壓配電網，進行電壓變化和能量傳輸。文獻[19]通過對交流供電線路供電能力的分析，推導出直流供電線路在不同約束條件下的供電能力的計算模型。不同于交流電網中的變壓器，整流器、逆變器和DC-DC變換器用來變換電壓和傳輸能量，其潮流計算模型與交流變壓器截然不同。同時，直流配電網中沒有無功功率和電壓相角，應根據直流配電網的特點對節點進行重新分類。

針對直流配電網潮流計算問題，本文建立考慮開關損耗及電感電容寄生參數的非理想變換器穩態模型，考慮到直流配網中只有有功功率與電壓幅值，直流變換器可采用不同控制策略的特點，提出適用于直流配網的牛頓拉夫遜法潮流計算模型。最后通過算例驗證該模型的合理性與有效性。

1 換流器潮流模型

1.1 整流器和逆變器的潮流模型

電壓源換流器(voltage source converter，VSC)用于直流配電網。電路圖如圖1所示。設交流側線電壓有效值為US，相角為δS，交流側的功率為PS、QS，換流器側的線電壓有效值為US，相角為δS，交流側往換流橋注入的功率為PC、QC，直流側的電壓為Ud，電流為Id，忽略交流濾波器，換流變壓器與換流電抗器可結合在一起用一個阻抗ZC=RC+jXC來等效。其潮流模型如圖2所示。

交流側功率為

(1)

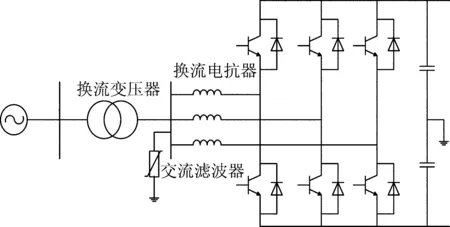
圖1 電壓源換流器主電路Fig.1 Main circuit of voltage source converter

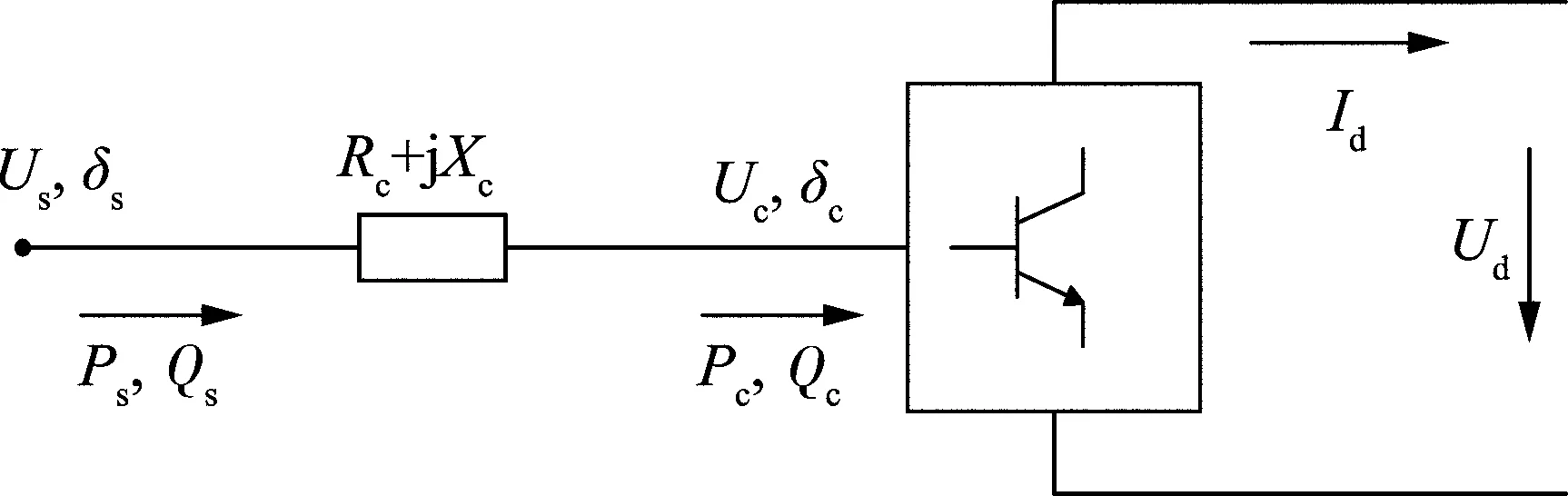
圖2 VSC的潮流模型Fig.2 Power flow model of VSC

換流器側功率為

(2)

直流側有功功率為

Pd=UdId

(3)

可用一個取決于換流器電流IC的統一公式來模擬換流橋損耗Ploss[9]:

(4)

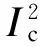
換流橋兩側的功率關系為

Pd=PC-Ploss

(5)

采用空間矢量脈寬調制(spacevectorpulsewidthmodulation，SVPWM)技術，M為脈寬調制比，換流橋輸出線電壓UC也可表示為直流電壓Ud的函數[12]：

(6)

1.2 CCM模式下DC-DC變換器潮流計算模型

變換器的工作狀態分為連續電流模式(continuous current mode，CCM)及斷續電流模式(discontinuous current mode，DCM)，臨界條件取決于電路中的周期、占空比、輸出電壓、電感值等因素[20],在周期、占空比、輸出電壓等參數給定情況下，只要電感足夠大，電路則工作于連續電流模式。基于以上假設，本文僅討論CCM模式下開關變換器的穩態模型。換流器建模時需考慮開關損耗及電感電容寄生參數。IGBT以開關Q及飽和壓降UQ的串聯作為導通時的模型，MOSFET以開關S和導通電阻RS串聯作為導通時的模型，二極管以開關D、正向導通壓降UD、導通電阻RD串聯作為其通態模型，電感線圈用理想線圈及電感電阻RL的串聯來等效，電容用理想電容與電容電阻RC的串聯來表示。

對于帶隔離的變換器而言，隔離變壓器也會產生損耗，由于隔離變壓器工作狀態不同，其主要損耗的等效參數也不同。對于反激型變換器，開關導通時，隔離變壓器二次側空載，開關斷開時，勵磁電感中儲存的能量向負載側供電，由于一次繞組電阻遠小于勵磁電阻，可將一次繞組電阻忽略[21]，因此隔離變壓器的損耗主要是空載損耗，等效模型應為理想變壓器與勵磁電感Lm及勵磁電阻Rm的并聯。對于正激型變換器，開關導通時，隔離變壓器傳遞能量向負載供電，開關斷開時，由電感向負載供電，此時隔離變壓器的損耗主要是一二次繞組電阻上的損耗，因此隔離變壓器等效成一二次繞組電阻RT1、RT2與理想變壓器的串聯。

借鑒文獻[17]提出的為CCM模式下非理想Boost變換器穩態建模的方法，本文考慮了開關損耗及電感電容寄生參數的CCM模式下非理想Buck、Buck-Boost、反激型、正激型、全橋變換器建立穩態模型。

該方法的基本思路是：

(1)建立包含元器件損耗的等效IGBT電路；

(2)在開關的導通及關斷階段，分別列出電感電壓及電容電流的表達式；

(3)不考慮開關高頻紋波，假設1個周期內電感電流及電容電壓恒定；

(4)1個周期內電感和電容吸收的能量與釋放的能量相等，則1個周期內電感電壓與電容電流的積分均為0；

(5)根據(4)中得到的公式建立等效穩態電路模型。

CCM模式下非理想變換器統一的穩態模型如圖3所示，表1中列出了Buck、Boost、Buck-Boost、反激型、正激型、全橋變換器的各項參數。其中Buck-Boost變換器的輸入電壓為-Ui，其余均為Ui。

圖3中，Ui為直流電源電壓，Ii為輸入電流，Uo為輸出電壓。在表1中，觸發信號的占空比為D，隔離變壓器變比為1∶n。其余參數前文已有介紹。

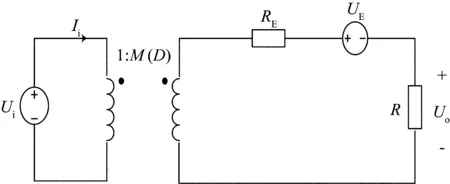
圖3 單個DC-DC變換器統一穩態模型Fig.3 Unified power flow model of a single DC-DC converters

中壓直流配電網與低壓直流配電網之間進行電能交換或直流變壓均要通過DC-DC變換器來進行。由于單個開關的耐壓水平和傳遞功率有限，單個換流器不能應用于高壓場合。屬于大電壓輸入大電流輸出場合，應采用輸入串聯輸出并聯(input-series output-parallel，ISOP)的拓撲結構，其結構圖如圖4所示。

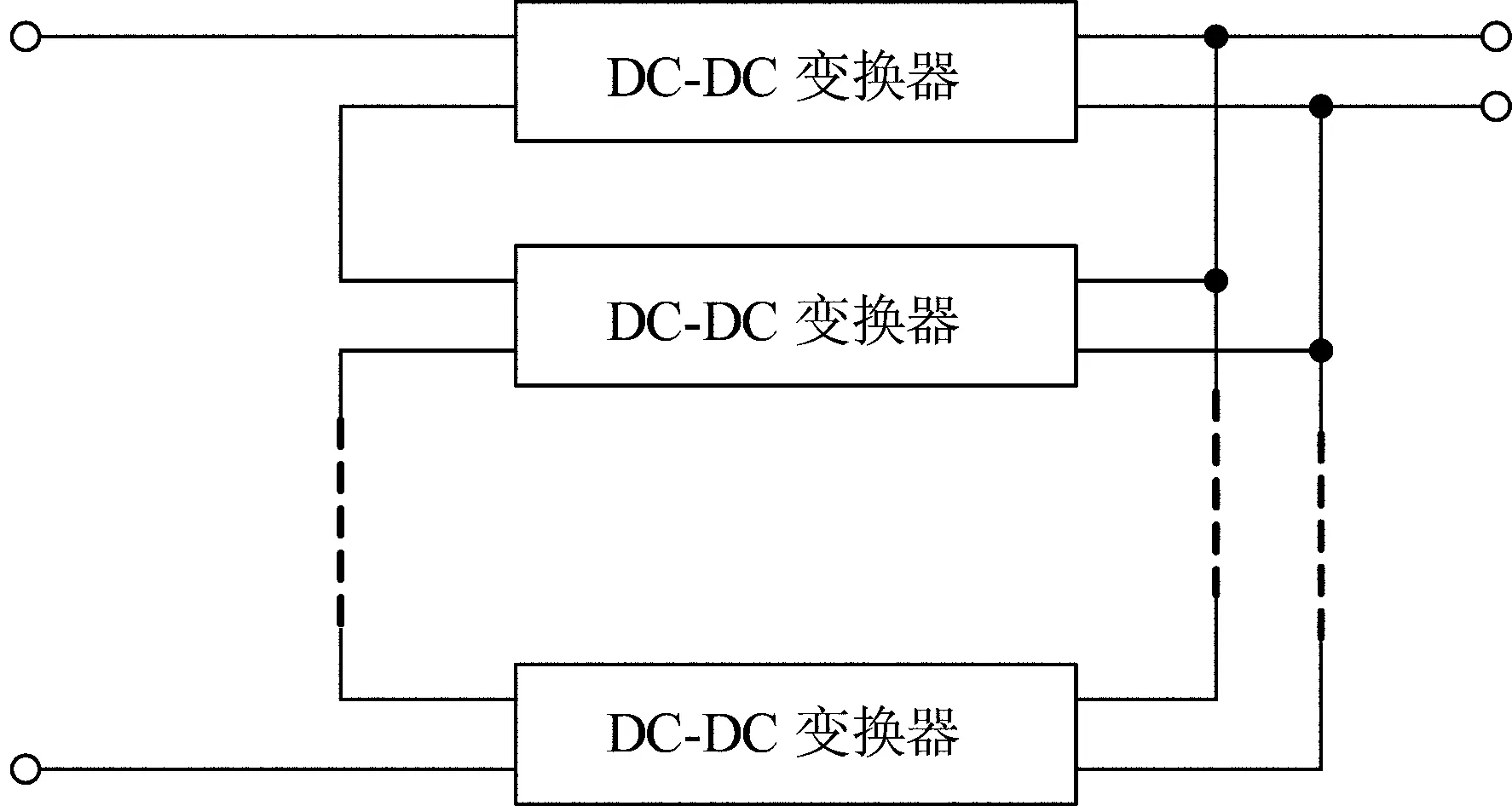
圖4 輸入串聯輸出并聯(ISOP)拓撲結構Fig.4 ISOP topology

設在ISOP的拓撲結構中有N個完全相同的變換器子模塊，在ISOP時的穩態模型如圖5所示。

圖5 ISOP拓撲下的穩態模型Fig.5 Steady-state model under ISOP topology

圖3、圖5和表1的模型也可以用于DC-DC變換器的閉環控制中。在直流配電網中，采用閉環控制來調節局部功率或電壓的某些DC-DC變換器可以直接視為V節點或P節點。另外，與交流系統中的變壓器類似，其余某些DC-DC變換器可以改變電壓等級。對于上述的DC-DC變換器，二次側電壓控制不變，一次側電壓未知。本文著重考慮變換器兩側電壓轉換關系而非針對閉環控制的具體過程。每次迭代的過程中，一次側電壓需更新。在上述情況下，為了采用DC-DC變換器的統一潮流模型，D僅僅是一個虛擬占空比，在每次迭代過程中變化靈敏并且反映了電壓關系。與交流潮流計算不同，由于D是節點導納矩陣中的可變參數，在每次迭代過程中節點導納矩陣需要更新。

2 直流配電網潮流計算模型

2.1 節點的分類及處理

在直流配電網中采用牛頓拉夫遜算法計算潮流。由于直流配電網中的物理量沒有無功功率與相角，因此可以將節點分為3類，一類是定P節點，即節點的注入功率P給定，另一類是定U節點，即節點電壓U給定，再一類是定I節點，即節點的注入電流I給定。

在穩態分析中，直接接入直流配電網的負載可視作定P節點，需要DC-DC變換器保持供電電壓恒定的直流負載可視作定U節點，需要DC-AC逆變器的交流負載可視作定I節點。

線路中實現升降壓功能的DC-DC變換器，根據其采用的不同控制方式，若是不調壓類型，出口側節點視作定P節點，若是采用定電壓控制，保持輸出電壓恒定，出口側節點視作定U節點。

交流電網、分布式電源以及儲能設備等均通過電力電子換流器接入直流配網，換流器采用定功率控制策略的視為定P節點，換流器采用定電流控制策略的視為定I節點，換流器采用定電壓控制策略的視為定U節點。在直流配電網中，像這類扮演電源角色的定U節點，同時也充當平衡節點，起著平衡潮流的作用。潮流計算過程中若發現這類節點的有功功率越限，則有功功率取其限值，定U節點轉化為定P節點。

2.2 電壓源換流器的處理

VSC用于交流電源和交流負載的接入。對交流電源來說，一般通過控制VSC保持直流電壓恒定，可直接參與直流配電網的潮流計算。對交流負載來說，一般通過控制VSC保持交流電壓恒定。因此交流側的電壓及功率為已知，這里假設直流配電網潮流計算第k次迭代得到直流側節點電壓為Ud(k)，第k+1次迭代時計算得到直流側的節點注入電流Id(k+1)。因此根據第2部分提出的潮流計算模型可得

(7)

式中M、δc是未知量，利用牛頓拉夫遜法求解式(7)。第m次迭代的不平衡量為

(8)

雅各比矩陣為

(9)

其中

(10)

則可建立修正方程式如下

(11)

第m+1次迭代的狀態量新值為

(12)

由于M在0～1之間，若假設內部第m次迭代求出的新值超出這個范圍，則令M=1，松弛交流電壓US，將其作為狀態變量，與δC一起繼續迭代求解。當滿足精度要求迭代收斂后，可根據式(1)—(6)求得電壓源型換流器直流側的電流。可以認為，整個直流配電網潮流計算是外部迭代，對換流器方程的求解為內部迭代，利用外部迭代第k次迭代的電壓Ud(k)，進行內部迭代求得的解作為外部迭代第k+1次迭代時脈寬調制(pulse width modulation，PWM)換流器直流側的節點注入電流Id(k+1)。

2.3 節點導納矩陣的建立

普通線路的導納等于線路電阻的倒數，而對于DC-DC變換器支路，可建立π型等值變換器模型，如圖6所示。

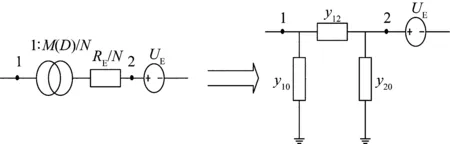
圖6 等值變換器模型Fig.6 Equivalent converter model

對圖6中等值前的原DC-DC變換器可列方程：

(13)

求解式(13)，可得

(14)

對圖7等值后的電路可列方程：

(15)

對照式(14)與式(15)，可得

(16)

當DC-DC采用不調壓控制方式時，此時占空比D是一定的，可直接建立節點導納矩陣并求解直流配電網潮流。而當DC-DC采用調壓控制方式，控制輸出電壓恒定時，此時占空比D是一個變化的數值。而由前面的分析可知，DC-DC變換器潮流模型中的參數M(D)、RE、UE與占空比D是相關的，D變化，M(D)、RE、UE也相應地會發生變化，此時為建立節點導納矩陣，需確定每次迭代時的占空比D。過程如下。

以首末端節點為I、J的變換器支路為例，找出其余與J節點相連的支路，設其另一端節點為1，2，…，m，利用第k次迭代的電壓求得各支路上流動的功率，與J節點本身所帶的負荷Pj相加得到第k次迭代時支路I-J末端的功率PJ。

(17)

式中RJx表示支路電阻。

用式(17)求得的PJ(k)值除以J點電壓從而求得第k次迭代時支路I-J上流過的電流IJ。

(18)

結合節點I電壓、變換器參數M(D)、RE、UE，求得第k+1次迭代的變換器占空比。

Buck變換器:

(19)

Boost 變換器:

(20)

式(20)中：

(21)

Buck-Boost變換器：

(22)

式(22)中：

(23)

反激變換器：

(24)

式(24)中：

(25)

對于Boost、Buck-Boost、反激變換器，占空比計算出有2個值，選取占空比在(0.1，0.9)內的值，忽略另一個。

正激變換器：

(26)

全橋變換器：

(27)

計算出第k+1次占空比后，能得出各類型變換器第k+1次的變比。

2.4 潮流計算方程

選擇狀態變量為節點的電壓值。設前n個節點均為注入功率P給定，第n+1～m個節點為注入電流I給定，計算模型如下：

建立節點導納矩陣Y，則節點注入電流為

I′=YU

(28)

由于DC-DC 變換器支路上還有一個UE的電壓降，因此其注入電流還需要相應的修正。設DC-DC變換器首末端節點分別為DI、DJ，式(28)得到的節點DI、DJ的注入電流為IDI′、IDJ′，修正后的值為IDI、IDJ。則有

(29)

記修正后的節點注入電流列向量為I，則可得注入功率的不平衡量

(30)

式中：Pg為定P節點給定的注入功率；Ig為定I節點給定的注入電流。

雅各比矩陣為

(31)

其中各元素為

(32)

則可建立修正方程式如下：

(33)

則第k+1次迭代的節點電壓新值為

U(k+1)=U(k)+ΔU(k)

(34)

2.5 潮流計算流程

直流配電網潮流計算具體流程圖如圖7所示。

圖7 直流配電網潮流計算流程圖Fig.7 Power flow calculation process of DC distribution network

3 算例分析

直流配電網如圖8所示。負荷功率單位為MW。節點1至5所在電壓等級為10 kV，節點6—14所在電壓等級為0.38 kV。節點1通過換流器與交流電網相連，視為無窮大電源。節點3、12上分布式電源均通過換流器接入。其中節點3上的分布式電源最大功率為5 MW，換流器初始時采用恒電壓控制。節點12上的分布式電源最大功率為0.6 MW，換流器初始時采用恒電流控制。各節點所帶負荷如圖所示，負荷功率單位為MW，節點13通過逆變器接入了交流負荷，節點8上是要求電壓恒定的直流負荷，用DC-DC變換器保證其電壓。

支路DC-DC變換器設置及參數如表2、3所示。節點13所接逆變器參數如表4所示。

圖8 直流弱環網Fig.8 DC weakly meshed network

表3 DC-DC變換器設置參數Table 3 Setting parameters of DC-DC converter

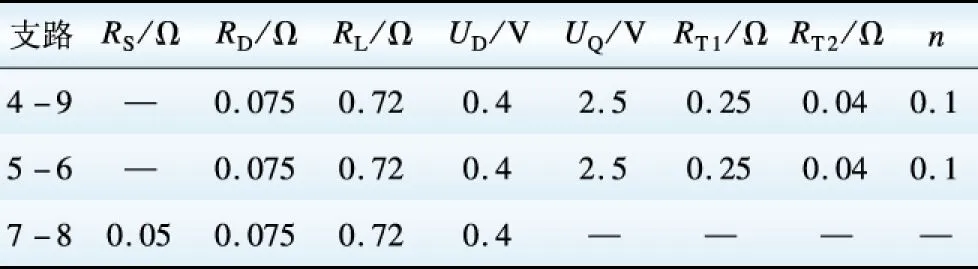
表4 逆變器設置參數Table 4 Setting parameters of inverter

初始時系統節點類型及節點數據如表5～7所示。

表5 定U節點數據
Table 5 Data of busUkV

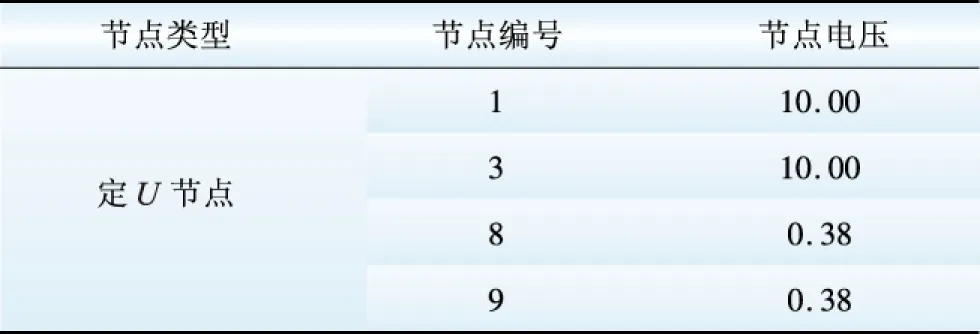
表6 定P節點數據Table 6 Data of bus PMW

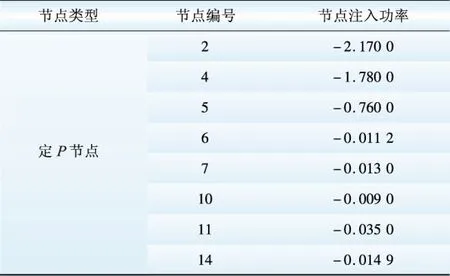
表7 定I節點數據Table 7 Data of bus IkA

該網絡中支路電阻如表8所示。

表8 支路電阻
Table 8 Line resistance Ω

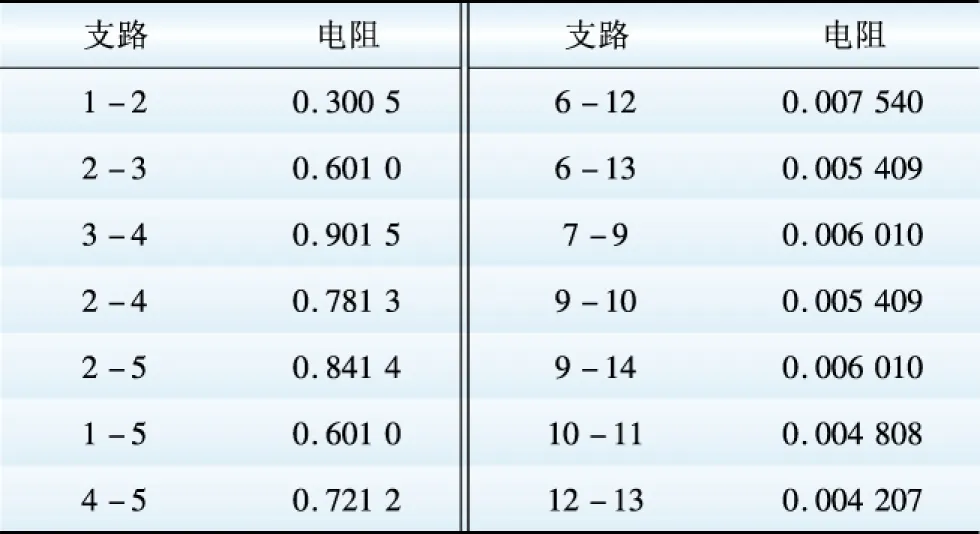
應用MATLAB編寫的程序計算該網絡潮流，得到的結果如表9—13所示。表9給出了潮流計算出的各節點電壓值，表10及表11給出了收斂后得到的電力電子換流器的參數值，表12給出了各支路功率損耗，表13給出了平衡節點注入功率。

表9 MATLAB計算的各節點電壓值
Table 9 Voltage value of each bus calculated by MATLAB kV

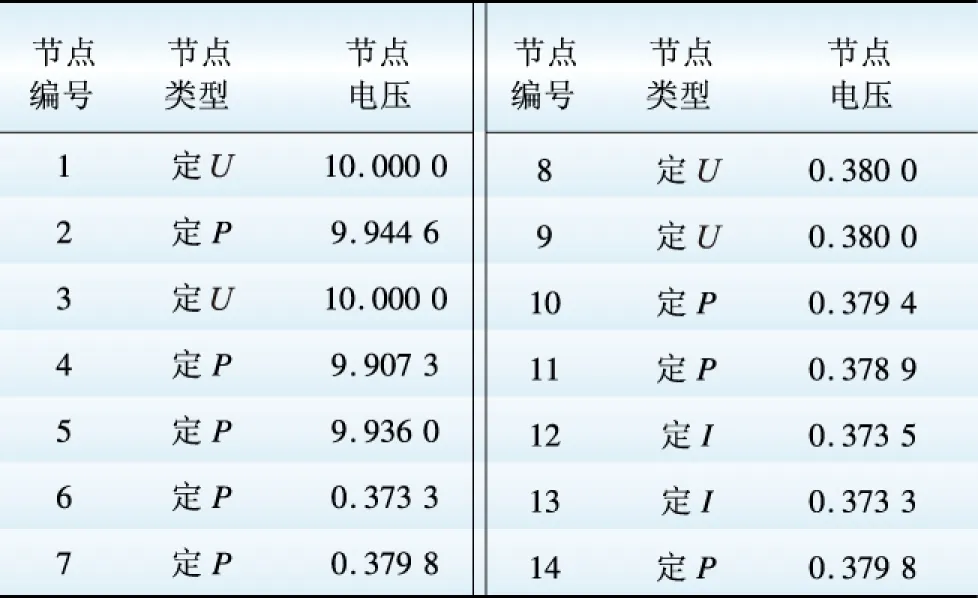
表10 計算出的DC-DC變換器參數值Table 10 Calculated DC-DC converter parameters

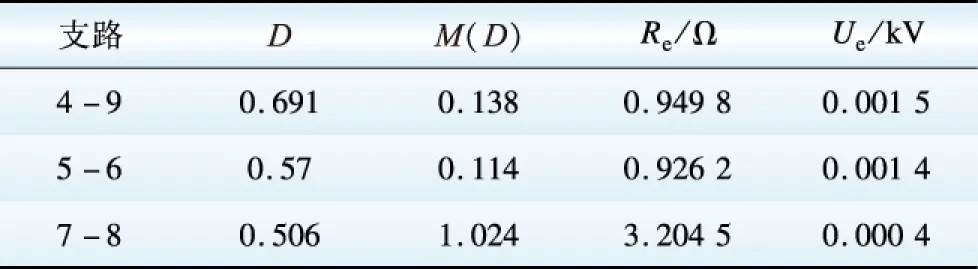
表11 收斂后DC-AC換流器參數值Table 11 Parameters of DC-AC converter after convergence

表12 各支路功率損耗Table 12 Power loss of branches MW

表13 平衡節點注入功率
Table 13 Injected power of balance bus MW

在計算結果中，節點6與節點13計算出的電壓其實有微小差異，但由于四舍五入的關系，最后節點6與13的電壓值相等，表格中的支路6-13上功率損耗為0。對于變換器支路4-9、5-6，2個變換器參數值相差不大，但由于流過變換器4-9的功率比5-6大很多，則變換器4-9上的功率損耗比變換器5-6上也大很多。

在PSCAD/EMTDC上對該弱環網進行仿真，得到結果如表14所示。

表14 PSCAD仿真結果
Table 14 Simulation results of PSCAD kV

比較MATLAB計算結果與PSCAD仿真結果，其誤差如表15所示。

表15 計算結果與仿真結果誤差 Table 15 Error between calculation results and simulation results %

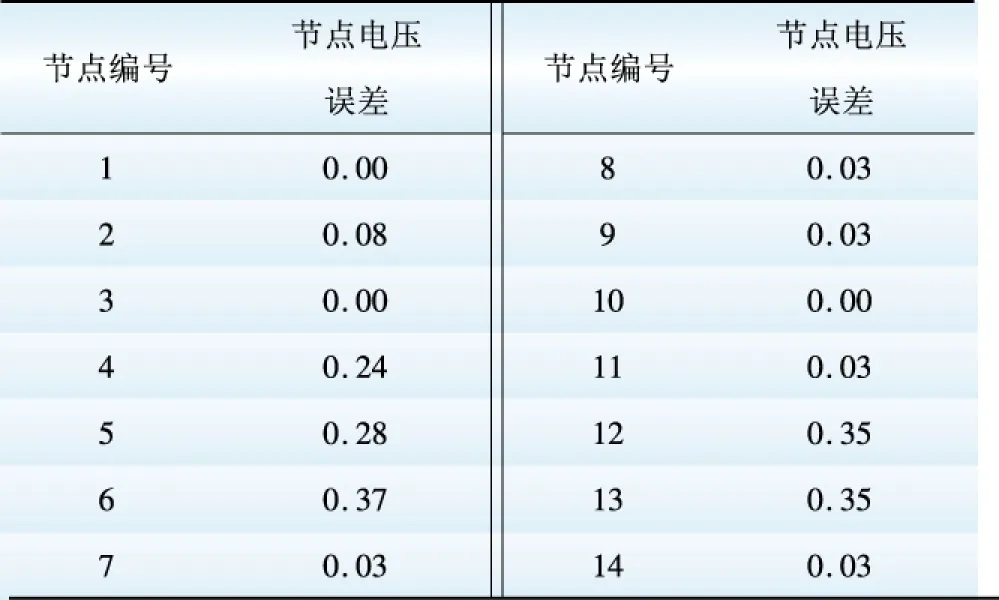
通過表15的誤差結果分析，可以看出由于加入了換流器支路，MATLAB計算出的電壓值與PSCAD仿真得到的電壓值存在了一定的誤差。其存在原因一是由于在本文的建模過程中為計算簡便省略了一部分損耗，二是由于在PSCAD仿真中，換流器的控制以及電感電容等參數的設置也有一定影響。例如在原本的設定條件下，節點9應保持0.38 kV，但仿真中由于控制的微小誤差，使得節點9的電壓值固定在了0.379 9 kV，從而對其余支路也造成了一定影響，而電感電容組成的濾波環節，其參數對波形效果影響很大，因此PSCAD仿真值只能作為一個參照。從誤差結果來看，最大為0.37%，在接受范圍內。此計算結果可以表明，本文建立的換流器穩態模型及每次迭代時AC-DC換流器支路的處理及DC-DC變換器變比的確定方法是有效的，直流配網的牛頓拉夫遜法的潮流計算模型對于計算弱環網絡是可行的。

以上算例中，網絡僅有14個節點。當直流配電網有更多的環路或者更復雜的拓撲結構時，盡管網絡結構變得復雜，但是直流系統的控制方法相對清晰，每個換流器的輸出都有一個相對應的控制策略，比如恒定電壓、恒定功率或者功率下垂控制，這些控制策略可以提供更多的節點信息。因此，一旦換流器的控制模式確定，即使拓撲結構相比本算例變得更為復雜，也對算法的有效性影響不大。

4 結 論

本文通過分析整流器、逆變器和DC-DC變換器，建立了考慮開關損耗和電感電容寄生參數的非理想換流器穩態模型。考慮到直流配電網中只有有功功率和電壓、DC-DC變換器需要保持輸出電壓恒定的特點，本文提出了應用于直流配電網的采用牛頓法拉夫遜算法的潮流計算模型。所建立算例的潮流計算結果驗證了所提出模型的合理性與有效性。

[1]LARRUSKAIN D M, ZAMORA I, ABARRATEGUI O, et al. Conversion of AC distribution lines into DC lines to upgrade transmission capacity[J]. Electric Power Systems Research,2011,81(7):1341-1348.

[2] HAMMERSTROM D J. AC versus DC distribution systems—did we get it right[C]// Proceedings of IEEE Power Engineering Society General Meeting, Tampa, FL, USA:IEEE,2007:1-5.

[3] STARKE M, LI F X,TOLBERT L M, et al. AC vs. DC distribution: maximum transfer capability[C]//Proceedings of IEEE Power and Energy Society General Meeting-Conversion and Delivery of Electrical Energy in the 21st Century, Pittsburgh, PA, USA:IEEE,2008:1-6.

[4] DASTGEER F, KALAM A . Efficiency comparison of DC and AC distribution systems for distributed generation[C]//Proceedings of Australasian Universities Power Engineering Conference, Adelaide, SA, Australia:IEEE,2009:1-5.

[5] MOHAMED A, MOHAMMED O. Power flow control in DC distribution systems[C]//North American Power Symposium, Arlington, TX, USA:IEEE,2010: 1-7.

[6] 宋強, 趙彪, 劉文華, 等. 智能直流配電網研究綜述[J]. 中國電機工程學報, 2013, 33(25): 9-19. SONG Qiang, ZHAO Biao, LIU Wenhua, et al. An overview of research on smart DC distribution power network[J]. Proceedings of the CSEE, 2013, 33(25): 9-19 .

[7] 江道灼, 鄭歡. 直流配電網研究現狀與展望[J]. 電力系統自動化, 2012, 36(8): 98-104. JIANG Daozhuo, ZHENG Huan. Reaearch status and developing prospect of DC distribution network [J].Automation of Electric Power Systems, 2012,36(8):98-104.

[8] 溫家良, 吳銳, 彭暢, 等. 直流電網在中國的應用前景分析[J]. 中國電機工程學報, 2012, 32(13)：7-12. WEN Jialiang, WU Rui, PENG Chang,et al. Analysis of DC grid prospects in China[J]. Proceedings of the CSEE, 2012,32(13):7-12.

[9] BEERTEN J, COLE S, BELMANS R .Generalized steady-state VSC MTDC model for sequential AC/DC power flow algorithms[J].IEEE Transactions on Power Systems, 2012,27(2):821-829.

[10] CHAI R Z, ZHANG B H, BO Z Q. Alternating iterative power flow algorithm for hybrid AC/DC networks containing DC grid based on voltage source converter[J]．Automation of electric power system, 2015, 39(7):7-13.

[11] LI G Y, ZHOU M, HE J. Power flow calculation of power systems incorporating VSC-HVDC[C]//2004 International Conference on Power System Technology, Singapore:IEEE,2004:1562-1566.

[12] 張弛, 江道灼, 葉李心, 等. 一種適用于直流配電網的雙向穩壓型電壓平衡器[J]. 電力建設,2013,34(10):53-59. ZHANG Chi, JIANG Daozhuo, YE Lixin, et al. A bi-directional voltage regulating balancer for DC power distribution network[J]. Electric Power Construction, 2013, 34(10): 53-59.

[13] HUSNA A.W.N, SIRAJ S.F, MUIN M.Z.A Modeling of DC-DC converter for solar energy system applications[C]//2012 IEEE Symposium on Computers & Informatics (ISCI), Penang:IEEE,2012:125-129.

[14] DIJK E V, SPRUIJT H J.N,SULLIVAN D M O, et al. PWM-switch modeling of DC-DC converters[J]. IEEE Transactions on Power Electrics, 1995,10(6):659-665.

[15] WANG Q, SHI L X,CHANG C Y. Small signal transfer functions for a single-switch buck-boost converter in continuous conduction mode[C]//ICSICT 2008.9th International Conference on Solid-State and Integrated-Circuit Technology, Beijing:IEEE,2008,:2016-2019.

[16] LUO F L, YE H. Small signal analysis of energy factor and mathematical modeling for power DC-DC converters[J]. IEEE Transactions on Power Electrics, 2007, 22(1):69-79.

[17] BAHRAVA S, MAHERY H M,BABAEI E, et al. Mathematical modeling and transient analysis of DC-DC buck-boost converter in CCM[C]//IEEE 5th India International Conference on Power Electronics (IICPE), Delhi:IEEE,2012:1-6.

[18] 張衛平, 關曉菡, 劉元超,等. DC-DC變換器穩態建模的教學方法[J].電氣電子教學學報,2008,3(5):101-104. ZHANG Weiping, GUAN Xiaohan, LIU Yuanchao, et al. Teaching method of building steady state models for DC- DC Converters[J]. JOURNAL OF EEE,2008, 30 (5): 101-104.

[19]劉自發, 李韋姝, 韋濤, 等. 直流配網線路供電能力分析[J]. 電力建設, 2014, 35(7):80-85. LIU Zifa, LI Weishu, WEI Tao, et al. Power supply capability of line in DC distribution network[J]. Electric Power Construction, 2014, 35(7):80-85.

[20] 張一工, 肖湘寧. 現代電力電子技術原理與應用[M].北京:科學出版社,1999.

[21] 李發海, 朱東起. 電機學[M]. 北京: 科學出版社,2007.

(編輯 劉文瑩)

Power Flow Calculation Model and Algorithm of DC Distribution Network

ZHAO Guankun

(School of Electrical and Electronic Engineering, North China Electric Power University, Beijing 102206, China)

DC distribution network has drawn widespread attention globally with its advantages such as larger transmission capacity and suitability for the access of distributed generation (DG). The present study on the DC distribution network is mainly in topology, energy efficiency, control and protection. According to the problem of power flow calculation in DC distribution network, this paper establishes the steady-state model of non-ideal converter with considering the switching loss and the parasitic parameters of inductance and capacitance, and gives the steady-state model parameters of buck, boost and other 6 kinds of converters under continuous current mode (CCM). According to the characteristics of DC grid, which means that in DC distribution network only active power and voltage need to be considered, and the converters have different control strategies, we propose a new power flow calculation model with Newton-Raphson Jacobian matrix including DC distribution network. We adopt the proposed model and method in the power flow calculation of typical 14-bus DC distribution network, and compare the results with that of PSCAD simulation, which verify the correctness of the proposed model and algorithm.

DC distribution network; power flow calculation model; converter; Newton-Raphson

國家自然科學基金資助項目(51577058)

TM 74

A

1000-7229(2016)05-0109-09

10.3969/j.issn.1000-7229.2016.05.016

2016-04-06

趙冠琨(1996),男,本科,主要研究方向為電力系統計算和分析。

Project supported by National Science Foundation of China (51577058)