六輪機器人逆運動學的幾何誘導迭代法研究

陳廣濤，呂偉新，彭俊杰

(1.上海大學 計算機工程與科學學院，上海 200444；2.中科院上海高等研究院，上海 201210)

六輪機器人逆運動學的幾何誘導迭代法研究

陳廣濤1，呂偉新2，彭俊杰1

(1.上海大學 計算機工程與科學學院，上海 200444；2.中科院上海高等研究院，上海 201210)

機器人控制對實時性要求高，其逆運動學的快速求解是機器人控制領域的重要問題。在傳統(tǒng)的逆運動學求解方法中，大多采用數值迭代的方法，該方法具有一定的通用性，但是該方法同時也有迭代收斂慢或者不收斂的問題。針對數值迭代法在機器人逆運動學求解過程中遇到的運算量大、收斂速度慢、結果唯一性難保證、無法確保實時性要求的問題，提出利用機器人機構的幾何特點加速迭代收斂的方法。研究機構的幾何特點，找出其表達參數，僅對必要的變量進行迭代運算，其他關節(jié)變量由機構幾何特點獲得的解析式求得。在滿足實時性要求的前提下，該方法能以較少的迭代次數達到需要的求解精度。六輪機器人是廣泛研究的一種月球探測車模型，機構較為復雜。針對該具體結構的數值仿真表明，該方法快速有效。

機器人逆運動學；迭代求解；幾何法誘導；搖臂式六輪探測車

0 引 言

機器人控制對實時性要求高，其逆運動學的快速求解是機器人控制領域的重要問題[1]。有些機器人無法采用解析方法求解逆運動學，采用數值解法就需要在給定時間內穩(wěn)定收斂，這不但要盡量減少求解運算量，還應該排除算法中的嘗試性環(huán)節(jié)。

解析法計算效率高，是保證實時性的首選，然而應用中有許多機構無法得到解析解，只能借助數值方法求解，通過選擇關節(jié)變量初值，迭代逼近真實解。數值迭代法雖然能達到給定精度的運動學方程逆解，但運算量大、收斂速度與結果唯一性難保證、無法確保實時性要求[1-2]。最嚴重的問題是，迭代次數難以預料、計算結果具有不確定的多解性、不能確保收斂[3]。早已有人認識到減少迭代參數的意義，例如，易科[4]采用構造并求解僅含有一個關節(jié)參數的非線性方程方法，把逆解問題轉化為迭代求解這個角度的問題，再進一步由解析式求得其他角度。雖然這類方法減少了計算量，但是仍然不能克服迭代是否收斂、是否存在多解的問題。

為此，文中提出一種利用機構的幾何特點輔助迭代求解的方法，可避免多解問題、確保快速收斂，從而解決機器人逆運動學求解的實時性問題。由于涉及幾何方法的問題通用性不顯著，難以概括總結出通用法則，以一個被美國NASA等研究機構廣為采用的搖臂式六輪探測車的機構模型[5-11]為例，詳細介紹了該方法的基本原理，并給出其數字仿真結果。

1 搖臂式六輪車幾何模型

文獻[6]所給出的搖臂式六輪月球探測車結構模型如圖1所示，主要由差動軸、主搖臂、副搖臂、車輪組成。其中差動軸中間的差動器使左右主搖臂相對于差動軸轉動的角度互為相反數[6]。

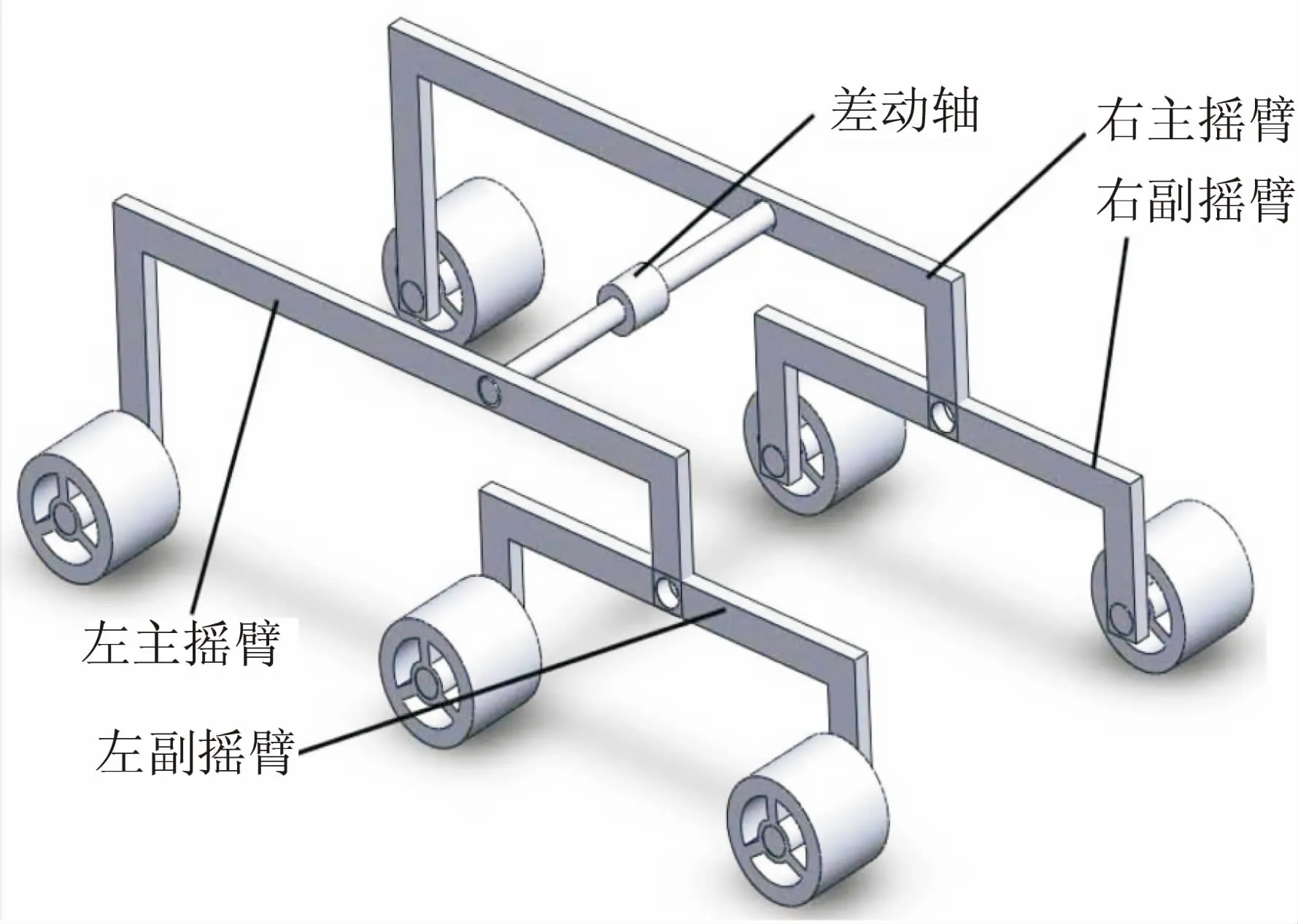
圖1 搖臂式六輪探測車結構

建立的空間坐標系如圖2、3所示。

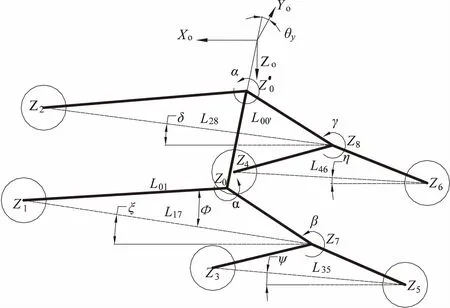
圖2 搖臂式六輪探測車空間姿態(tài)

定義左右主搖臂之間的差動角度分別α和-α，左右副搖臂相對其主搖臂的轉角分別為β和γ。定義差動軸坐標系OD-XDYDZD相對于空間絕對坐標系OO-XOYOZO的前向傾角為θx，側向傾角為θy，如圖3所示。可知，關節(jié)角{θx,θy,α,β,γ}確定后，各車輪的相對空間坐標隨之確定，反之亦然[6]。

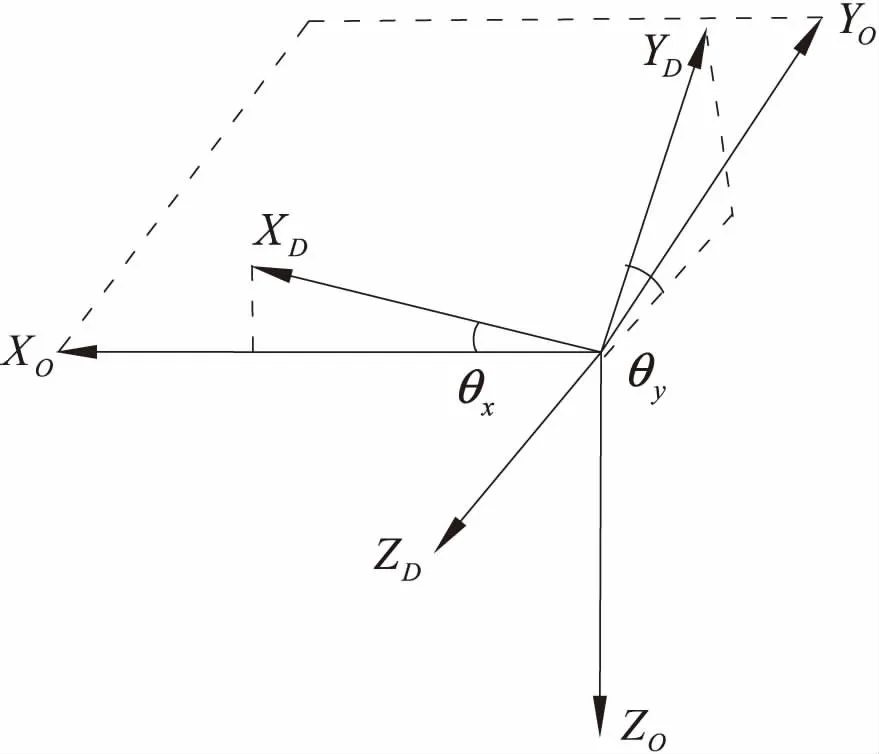
圖3 差動軸坐標系與空間絕對坐標系相對關系

應用中感興趣的是其6個輪心的相對高度與關節(jié)變量的關系，以便主動地適應月球的起伏地面。因此，其逆運動學求解問題就是如何從6個輪心的相對高度(即6個輪心在絕對空間坐標系ZO軸上的分量)得知關節(jié)變量{θx,θy,α,β,γ}。為此，以6個輪心等高的狀態(tài)作為初始狀態(tài)，并始終把最低的輪心高度設為零[7]。

2 利用幾何特征引導迭代過程

2.1 幾何特征分析及關系方程建立

文獻[6]給出的探測車結構尺寸如圖4所示。

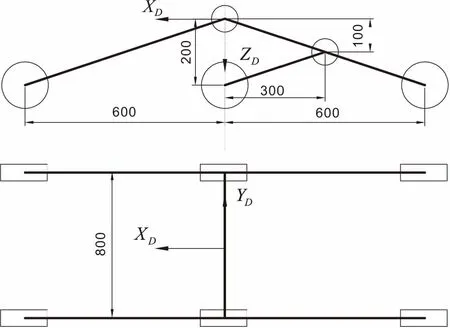
圖4 搖臂式六輪探測車結構尺寸

若是以常規(guī)方式建立探測車的運動學方程，得到的是多個矩陣相乘而形成的復雜方程組，難以簡化處理[6]。

利用圖2所示幾何關系易得到以下關系式：

(1)

(2)

(3)

(4)

(5)

(6)

(7)

Z0=Z1-L01sin(φ-ξ)cosθy

(8)

那么，容易通過中間變量表示所求關節(jié)變量：

(9)

(10)

其中，ξ0為初始狀態(tài)，即6個輪心在同一高度時ξ應該取得的值。

2.2 幾何特征引導迭代過程

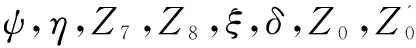
之所以選擇θy作為迭代變量，首先是因為這樣做可以把復雜的空間幾何問題簡化為平面上的問題，通過XDZD平面上的幾何關系直接得到θx,α,β,γ的解析表達式。更重要的是，能夠根據θy的幾何意義直觀地判斷迭代必然收斂于一個唯一值，避免了丟失可能解和盲目探索可能解的問題。因此，選擇適當的迭代變量是誘導迭代過程簡化計算逆解問題的關鍵[12]。

利用幾何關系輔助迭代求解逆運動學方法的思想是：找出機構運動過程中一個確定的幾何規(guī)律，利用該規(guī)律誘導迭代過程，避開不利方向，將描述該規(guī)律的參數選作迭代變量；采用盡可能少的變量表示其他關節(jié)變量，僅對必要的變量進行迭代運算，其他間接變量或關節(jié)變量均由解析式求得[13]。

本例中θy≠0是造成計算困難的關鍵，而且它在引導方向上只有一個可能解，就只可能收斂于一點。由于每次更新都相當于修正了前一次假設的誤差，因此能夠保證足夠的收斂速度。

3 數值仿真與分析

分別用常規(guī)數值求解法和文中提出的幾何輔助誘導迭代的數值法對文獻[6]中的機構實例進行求解，以驗證算法的有效性。其常規(guī)數值求解采用Matlab的fsolve函數對6元非線性方程組進行迭代求解，細節(jié)見文獻[6]。經對比發(fā)現，在所涉及表達式上，常規(guī)法求逆解的運算量明顯比幾何誘導法大，需要消耗更多的時間。再從迭代次數和時間消耗方面對比分析兩種算法。為此選擇了關節(jié)變量{θx,θy,α,β,γ}的三組不同值,通過正運動學方程求得其對應的6個輪心的高度值，然后反過來利用輪心高度作為所求逆解的已知值來求取關節(jié)變量，觀察結果與事先選定的關節(jié)變量理想值的一致性[14]。為避免所用初值不同造成的影響，三組計算的迭代初值統(tǒng)一選為{θx,θy,α,β,γ}={0,0,0,0,0}，而幾何誘導法的迭代初值也選用θy=0，兩種算法計算結果所允許的誤差均為ω=1×10-4。測試采用主頻為2.0GHz，內存為2.0GB的WindowsXP系統(tǒng)MATLAB平臺。實驗數據如表1所示,其中求逆解計算所消耗的時間采用10 000次計算后的平均值。

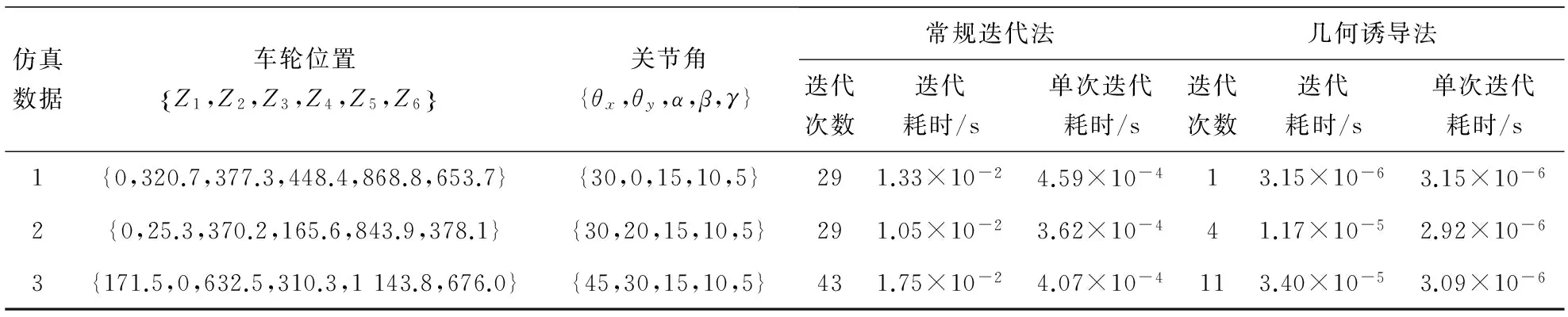
表1 實驗結果對比

由實驗數據可以看出：幾何誘導法的迭代次數遠小于常規(guī)逆解法，所耗費的時間是常規(guī)逆解法的幾千分之一甚至更少，特別地，當θy=0時，幾何誘導法僅迭代1次即得到理想值。可見，在迭代次數與計算耗時方面，幾何誘導法都明顯優(yōu)于常規(guī)逆解法。

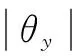
4 結束語

運動方程的常規(guī)逆解法直接從機器人的運動學方程出發(fā)，采用數學工具進行多元迭代，求解非線性方程組[14]；而幾何誘導法充分挖掘利用機器人機構的幾何特點[12]，采用盡可能少的關節(jié)變量表示其他關節(jié)變量，僅對必要的關節(jié)變量或某一中間變量進行迭代求解[15]，在同樣的運算精度要求下減少了迭代次數，單次迭代運算量也大為減少，極大地縮短了求解時間，并且避免了一般多元非線性方程組迭代方法中致命的收斂性問題，能更好地滿足機器人控制的實時性和準確性要求。

[1] 陳 鵬，劉 璐，余 飛,等．一種仿人機械臂的運動學逆解的幾何求解方法[J]．機器人,2012,34(2):211-216．

[2] 祖 迪，吳鎮(zhèn)煒，談大龍．一種冗余機器人逆運動學求解的有效方法[J]．機械工程學報,2005,41(6):71-75．

[3] 畢諸明，蔡鶴皋．六自由度操作手的逆運動學問題[J]．機器人,1994,16(2):92-97．

[4] 易 科．機器人運動學逆的數值迭代法[J]．計算技術與自動化,1992,11(2):26-30．

[5] 李所軍，高海波，鄧宗全．搖臂式月球車的運動學建模及懸架參數優(yōu)化[J]．西安交通大學學報，2009,43(9):62-66．

[6] 周開波，王旭永，羅小桃,等．搖臂式六輪探測車空間姿態(tài)建模與求解[J]．上海交通大學學報，2013,47(7):1093-1098．

[7] 毛 寧．六輪搖臂巡視器建模仿真及試驗研究[D]．長春：長春理工大學，2014．

[8] 胡 明，鄧宗全，高海波,等．搖臂轉向架式月球探測車越障通過性分析[J]．上海交通大學學報，2005,39(6)：928-932．

[9] 王佐偉，梁 斌，吳宏鑫．六輪月球探測車運動學建模與分析[J]．宇航學報,2003,24(5):456-462．

[10] 楊艷春，鮑勁松，金 燁．基于虛擬現實環(huán)境的六輪月球車運動性能分析[J]．上海交通大學學報,2010,44(8):1079-1083．

[11] 居鶴華，曹 亮，崔平遠．基于模糊邏輯的月球車逆運動學求解方法[J]．宇航學報,2009,27(4):643-647．

[12] 劉 達，王田苗．一種解析和數值相結合的機器人逆解算法[J]．北京航空航天大學學報，2007,33(6):727-730．

[13] 蔡自興．機器人學基礎[M]．北京：機械工業(yè)出版社，2009:15-26．

[14] 宋小康，談大龍，吳鎮(zhèn)煒,等．全地形輪式移動機器人運動學建模與分析[J]．機械工程學報,2008,44(6):148-154．

[15] 王慶國，林建亞，路甬祥．機器人的運動學與動力學[J]．機器人,1990,12(1):58-64．

Exploration of Geometric Inducing Method in Numerical Iteration for Six-wheeled Robot Inverse Kinematics

CHEN Guang-tao1,Lü Wei-xin2,PENG Jun-jie1

(1.School of Computer Engineering and Sciences,Shanghai University,Shanghai 200444,China;2.Shanghai Advanced Research Institute,Chinese Academy of Sciences,Shanghai 201210,China)

The automatic control of robot has a higher requirement of real-time,and it is important for automatic control to get the solution of robot inverse kinematics.In the traditional method,the solution by numerical iteration is always used,which is universal,but with the problems of slow convergence or non-convergence.Numerical iteration applied to robot inverse kinematics solution may bring the disadvantage of heavy calculation,slow convergence,the unique result not to guarantee,and good real-time performance not to determine.Therefore,a method using the geometric characteristics of robot mechanism is demonstrated to accelerate iteration convergence.It tries to find the parameters describing the geometric characteristics of mechanism studied,and need merely calculation of the iteration of key variables,while the other variables can be obtained by the analytic formula figured out by the geometric characteristics of mechanism.Applying the method can achieve the required precision by less number of iterations on the premise of meeting the real-time performance.Six-wheeled is a model of robot rover which has extensive research and complex mechanism.Numerical simulation of concrete mechanism shows the availability and high efficiency of the method.

robot inverse kinematics;iterative solution;geometric induction;six-wheeled rocker rover

2016-01-07

2016-04-19

時間：2016-11-21

國家自然科學基金資助項目(61572305)

陳廣濤(1988-)，男，碩士，研究方向為機器人、機器視覺；呂偉新，博士，教授，研究方向為機器人學、自動化、機器視覺等；彭俊杰，博士，副教授，CCF會員，研究方向為云計算、嵌入式系統(tǒng)等。

http://www.cnki.net/kcms/detail/61.1450.TP.20161121.1633.018.html

TP301

A

1673-629X(2016)12-0041-04

10.3969/j.issn.1673-629X.2016.12.009