電壓矢量細分的感應電機DTC滑模變結構控制

佘致廷，鄒 薇，熊克勤，譚瓊瓊，盧文斗

(湖南大學，長沙 410082)

電壓矢量細分的感應電機DTC滑模變結構控制

佘致廷，鄒 薇，熊克勤，譚瓊瓊，盧文斗

(湖南大學，長沙 410082)

通常造成感應電機轉矩直接控制局限性的關鍵問題在于低速情況下的轉矩產生脈動磁鏈和控制開關頻率波動無法固定。設計了基于轉矩與磁鏈滑模變結構異步電機直接轉矩控制器。此控制器設計的輸入信號分別采用定子磁鏈誤差、電磁轉矩誤差等信號，輸出信號采用12個細分電壓矢量DTC空間矢量合成電壓空間矢量。與傳統的方案中將滯環比較器以及開關電壓矢量選擇表應用到DTC中相比，這個控制器具有磁鏈控制更為準確、轉矩控制更為精細的特點，同時還能確保逆變器保持恒定的開關頻率。最終的仿真以及實驗的結果說明該控制方法具有有效性和可行性。

感應電機；直接轉矩控制；滑模變結構；電壓空間矢量

0 引 言

DTC是傳統感應電機的直接轉矩控制，定子靜止的坐標系里可以完成估計轉矩和磁鏈的工作，系統里將一些環節都已省掉，如坐標變換、電流調節器與脈寬調制器，該系統擁有較多優點，如系統的結構簡單、動態響應的速度快、優良的控制性能等[1-2]，然而，該方法仍然存在不足：例如容易使低速運行狀態下的感應電機的轉矩值過高，電壓逆變過程中控制IGBT開關的頻率無法固定、意見無法解決的脈動電流等問題[3]。眾多文獻中，針對此類問題的解決辦法一般概括為以下幾種：(1)提出細分化電壓空間矢量同時生成更復雜的開關矢量表；(2)為了使電機的低速轉矩脈動降低，由SVPWM產生可以維持恒定逆變器開關頻率的電壓的矢量表[7-13]。以模糊邏輯為基礎的占空比控制器使轉矩脈動降低，這是文獻[3]提出的辦法；文獻[4]采用改進開關矢量表，研究增加電壓矢量的控制方法。先通過SVPWM方法用于生成電壓空間矢量針對電壓矢量的控制方法，然后采用調節PI環進而達到轉矩和磁鏈的相應調整，最后，將目標需要得到的指定大小和方向的電壓矢量，通過基本單位下的空間電壓矢量按規定的算法合成[2，5-6]。文獻[5]提出的設計是以轉矩PI調節器與磁鏈為基礎，而當負載發生變化時，這一設計適應此時的優化控制存在一定難度；文獻[6]為降低電機在低速運行下轉矩脈動，提出采用調整有效矢量、零矢量的順序和各矢量的作用時間方案完善SVPWM。文獻[7]利用滑模原理、空間矢量控制與直接轉矩控制，對提高交流電機魯棒性、快速性以及抗轉矩脈動的可行性進行了深入研究。本文在文獻[8-12]研究的基礎上，提出了一種基于雙滑模變結構感應電機控制運行。傳統的DTC中有兩個滯環的比較器，采用磁鏈和轉矩滑模控制器替代它們，同時將12個細分的電太空間矢量的調制策略加入其中，合成需要的任意空間控制矢量，實現更準確的磁鏈控制以及更精細的轉矩控制，并保證逆變器開關頻率恒定。將其運用于感應電機電動汽車控制平臺，明顯提高了DTC系統的自適應能力。

1 數學模型的建立

在定子靜止坐標系下以空間矢量的形式表示感應電機電壓方程：

(1)

式中：p是微分算子；p是電機極對數；ωr為轉子速度，即電機轉速。

首先，我們采用定子靜止坐標系下電流磁鏈矢量按照給定方程(1)的方式實現針對于電機轉矩和磁鏈的控制算法，表達形式如下：

(2)

定子磁鏈幅值計算方法為：

(3)

電磁轉矩計算方法在定子靜止坐標系下：

(4)

按矩陣形式，將定子磁鏈參考坐標下的控制和狀態矢量分別按列寫成如下形式：

X=[isα,isβ,ψsα,ψsβ]T

(5)

則式(2)可用相量的形式表示：

(6)

式中：b1=(RsLr+RrLs)/σLsLr，b2=-ωr，b3=1/σLsTr，b4=ωr/σLs，b5=Rs，t=1/σLs。

2 DTC滑模變結構設計

2.1 DTC控制結構

本文在空間矢量電壓調制技術的SVM-DTC系統中制定了一種新型的控制優化策略，這種策略主要是通過改變轉矩磁鏈的雙滑模結構得到的。首先，本系統利用定子磁鏈以及轉矩之間產生的誤差，將其作為一種基準，通過傳統的空間矢量電壓調制方法得出一個最優的電壓矢量，然后將該電壓矢量施加于感應電機，以滿足電機的轉矩與磁鏈的最好的補償。同時也能兼有穩定逆變器的開關頻率及降噪的作用。

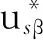
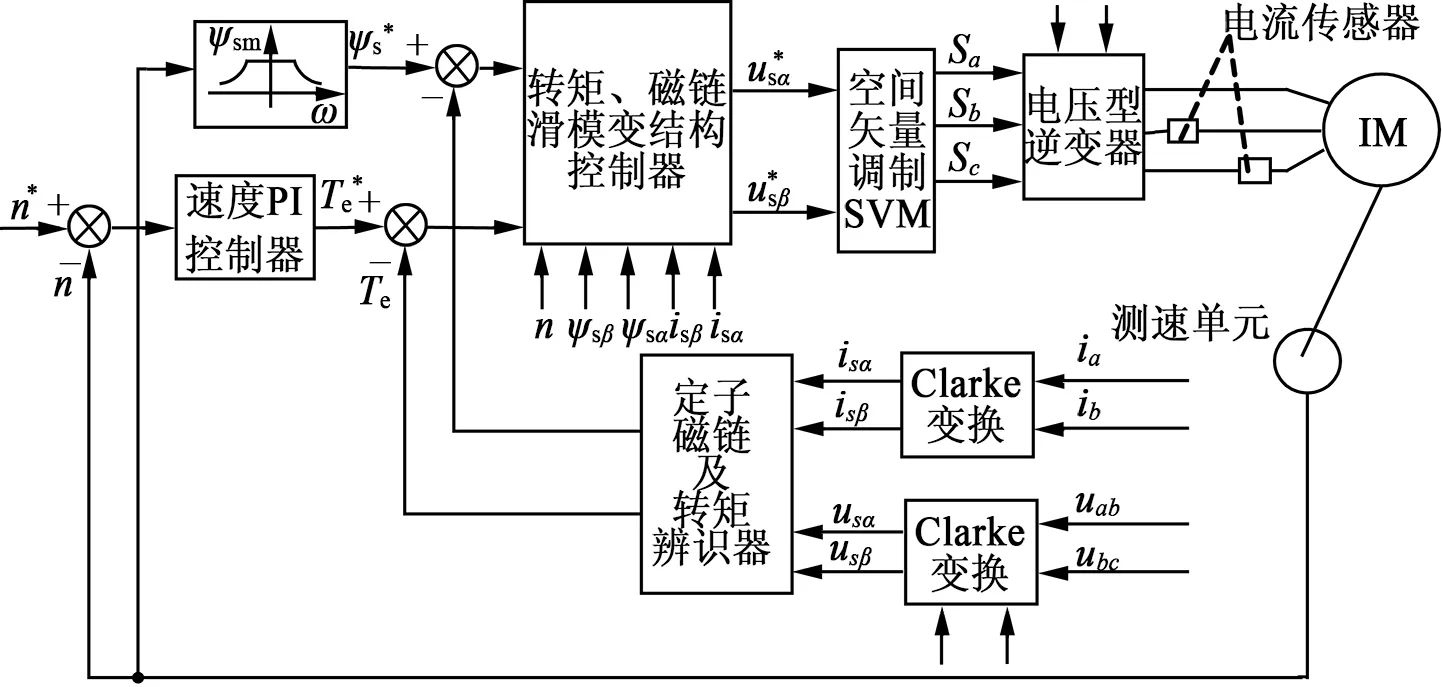
圖1 基于SVM-DTC磁鏈與轉矩滑模變結構控制感應電機系統原理框圖

定子磁鏈、轉矩估算方程在靜止α-β坐標系下：

(7)

(8)

(9)

(10)

(11)

2.2 積分滑模面設計

基于直接對磁鏈和轉矩進行控制原理，該DTC滑模變結構系統選用積分滑模面，如圖(12)所示，從而確保滑模變結構系統的穩定性，改善動態性能：

(12)

由式(12)可得：

(13)

下面進一步對式(13)進行推導。 由式(1)可得：

(14)

由式(7)和式(8)可得：

(15)

由式(9)、式(11)及式(14)、式(15)分別對定子磁鏈和電磁轉矩求導，可得：

(16)

Ψs=-2RsΨaia-2RsΨβiβ+2Ψaua+2Ψβuβ

(17)

則可進一步得到：

2Ψαuα-2Ψβuβ+KΨeΨ

(19)

利用指數趨緊率，對滑模控制器進行設計，在正常的運動階段中，實現動態品質佳的滑模控制系統,如下：

(20)

式中：K1,K2,K3,K4為正常數。 則可得：

-ST[K1ST+K2sign(ST)]-

SΨ[K3SΨ+K4sign(SΨ)]

(21)

式中，因為ST與[K1ST+K2sign(ST)]符號相同，所以ST[K1ST+K2sign(ST)]>0；同理可得，SΨ[K3SΨ+K4sign(SΨ)]>0。由此可知，STS<0這一系統能完成滑模運動，它是存在可達性與存在性的。

根據式(11)～式(13)可得：

(22)

則VSS控制率可設計：

(23)

式中：K2,K4一般取小一些，K1,K3則選大一些。這使在離切換面遠的地方，系統切換面更為迅速些，使正常的運動階段中，成功的加快了動態效應；另外，系統離切換面近的地方，能確保速度更加暖慢，當滑模切換時，成功地減小了抖振這一現象。

3 多電壓矢量的DTC-SVM

相比于采用6個非零電壓矢量和2個零矢量通過查表法生成PWM的傳統的直接轉矩的控制辦法，因為電機中只加入了很少的電壓矢量數量，電流與轉矩脈動不可避免。從而，本文采用十二扇區細分磁鏈空間，十二電壓控制矢量細分電壓以解決這個問題。具體詳細方法介紹如下：在現有電壓矢量的基礎上，根據其兩兩之間60°的角平分線方向設計出6種不同的新電壓矢量，這樣就可以相應地在空間中建立12個不同的電壓矢量(如圖2所示)，將其作為基準電壓，從而使得空間電壓矢量的精度獲得提高。

圖2 空間電壓矢量的方向以及區域

圖3中，把上述的12個電壓空間矢量進一步進行劃分，得到更為精確的電壓控制矢量。

圖3 空間控制矢量電壓分解圖

圖3中，基本的電壓矢量V23與V21共同合成了電壓矢量V2，兩個相鄰的電壓矢量V2,V1，零矢量V70和V00共同合成了電壓矢量Vref可用下式來表達：

(24)

這里，T00，T1，T2，T70是矢量V00，V1，V2，V70的作用時間；TS是采樣周期；為了計算T00，T1，T2，T70按圖2列出如下方程：

(25)

(26)

(27)

(28)

(29)

借助上面的算法和電壓矢量擁有的合理控制，進行完成作用時間的計算，使逆變器中擁有永遠恒定的開關頻率。

DTC的定子旋轉中，它的d-q坐標系內，轉矩、轉矩的電壓矢量和定子磁鏈的方程，如下：

(30)

(31)

(32)

由式(30)～式(32)可推導出：

(33)

(34)

4 仿真和實驗分析

圖4是以MATLAB 7.8/Simulink為環境，對DTC仿真的模型進行完善，建立新的仿真模型[15-16]。

圖4 感應電機DTC變結構控制系統仿真模型

將傳統的DTC系統控制的性能、磁鏈以及感應電機受轉矩滑模變結構控制的DTC系統為基礎，對DCT系統的轉矩靜態與動態的響應性能進行探討。

進行仿真研究。實驗中設定電機運行情況：(1)該電機的轉速是100 r/min，在0.05 s時刻在電機上加上一個 的轉矩，在0.12s時刻施加一個-5N·m的轉矩，在0.2 s時刻又將施加的轉矩變為+5 N·m；(2)轉速為1000r/min，負載轉矩+5～-5 N·m。實驗采用感應電機參數為：Pn=4 kW，Un=400V，fn=50Hz，nn=1430r/min，p=2，Lr=0.005838 H，Rr=1.390 Ω，Ls= 0.005 838 H，Rs=1.400 Ω,Lm=0.172 2 H，Tn=40 N·m，J= 0.013 1 kg·m2。給定磁鏈幅值1.1 Wb，滑模變結構控制器趨近律參數給定為：λ1=40,m1=5,λ2=20,m2=2。電機運行情況(1)下，傳統感應電機DTC系統感應電機DTC變結構控制系統的仿真如圖5、圖 6。電機運行情況(2)下，圖 7所示為感應電機DTC變結構控制系統的仿真結果。

從圖5(a)可以看出，定子磁鏈在低速時明顯脈動較大，其磁鏈軌跡為不規則的圓形；從圖6(a)可以看出，定子磁鏈幅值較為穩定且軌跡曲線比較接近圓；從圖5(b)可以看出，在傳統的感應電機上使用的DTC系統，當首次施加的轉矩是+5 N·m時，其最終的響應會相對較差，同時還會產生較大的脈動；從圖6(b)可以看出，當突然改變轉矩時，會加快其響應的速度，減小轉矩的脈動。通過在感應電機上使用DTC變結構控制系統，得到圖7的仿真結果，從中可以看出，當電機在進行高速運轉時，其磁鏈以及轉矩的性能均表現良好，包括了靜態性能以及動態性能。

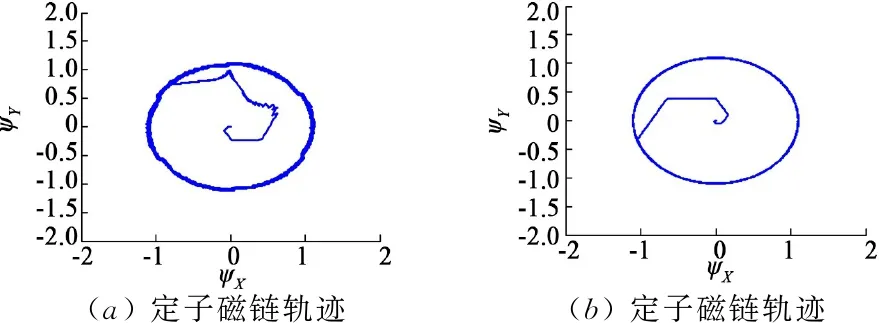
圖5 傳統感應電機DTC系統仿真結果

圖6 感應電機DTC變結構控制系統仿真結果

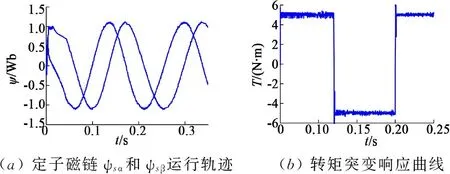
圖7 轉速為1000 r/min時感應電機DTC變結構控制系統仿真結果

為了驗證以上理論的正確性，本文以TMS320F28335為主控芯片，試驗中用到的仿真參數和感應電機參數是相同的，以磁鏈變的結構控制和轉矩為基礎，建立的的感應電機DTC系統實驗平臺上，定子的磁鏈大小為0.4 Wb，負載的轉矩設定為40 N·m，在實驗的過程中，考慮轉矩由+40 N·m突然變化為為-40 N·m的情況，對其實驗的結果進行研究，分為以下2種情況。

(1)假如將電機的轉速設置為100 r/min時，分別用 和 表示定子磁鏈的不同運行軌跡，圖8～圖10表示了轉矩在發生變化后的具體響應情況，以及A相定子的電流波形。

(2)假如將電機的轉速設置為1 000 r/min時，分別用ψsα和ψsβ表示定子磁鏈的不同運行軌跡，圖11～圖13表示了轉矩在發生變化后的具體響應情況，以及A相定子的電流波形。

由圖8～圖10可知，電機低速運行時，磁鏈以及轉矩的響應軌跡顯示出，其脈動的幅度很小。同時，A相電流為很好的正弦波波形。由圖11～圖13可知，電機在高速運行時，定子的磁鏈軌跡曲線表現相對平滑，而轉矩的脈動情況更不明顯，A相的定子電流波形畸變程度也特別小。

通過以上的實驗，其最終的結果說明了感應電機DTC轉矩與磁鏈變結構系統在靜動態性能方面表現優異，并能顯著改善電機在低速時的相關性能。

5 結 語

本文設計感應電機系統基于SVM-DTC磁鏈與轉矩滑模變結構控制器，在現有電壓矢量的基礎上，設計出六個新型的電壓矢量，從而在空間產生12個基準的電壓空間的矢量。將這12個基準的電壓空間的矢量為基礎，合成更加精準的任意電壓空間矢量。所以，這一控制方法能夠更加準確的跟蹤并控制轉矩和磁鏈的誤差。仿真與實驗后得出的結果告訴我們：通過該控制系統的使用，可以有效降低電磁轉矩的脈動。結果顯示，定子的磁鏈軌跡更加接近于園，也能具有較快的動態響應，且在速度較低時，其控制性能依然會保持良好。

[1]TAKAHASHII,NOGUCHIT.Anewquickresponseandhighefficiencycontrolstrategyofaninductionmotor[J].IEEETransactionsonIndustryApplications,1986,22(5):820-827.

[2] 佘致廷,張紅梅,何雯，等.感應電機DTC轉矩與磁鏈模糊PI自校正控制[J].電力系統及其自動化學報,2012,24(3):22-27.

[3]BUJAGS,KAZMIERKOWSKIMP.DirecttorquecontrolofPWMinverter-fedACmotors-Asurvey[J].IEEETransactionsonIndustrialElectronics,2004,51(4):744-757.

[4]SRINIVASAY,BABUK，TULASIRDG.Improvementindirecttorquecontrolofinductionmotorusingfuzzylogicdutyratiocontroller[J].ARPNJournalofEngineeringandAppliedSciences,2010，5(4):68-74.

[5]DOMENICOC,FRANCESCOP,GIOVANNIS,etal.FOCandDTC：twoviableschemesforinductionmotorstorquecontrol[J].IEEETransactiononPowerElectronics,2002,17(5):779-786.

[6]XUEY,XUX,HABETLERTG,etal.Alowcoststatorfluxorientedvoltagesourcevariablespeeddrive[C]//IEEEIndustryApplicationsSocietyMeeting.IEEE,1990:410-415.

[7]LAIYS,HENJHC.Anewapproachtodirecttorquecontrolofinductionmotordrivesforconstantinverterswitchingfrequencyandtorqueripplereduction[J].IEEETransactionsEnergyConversion,2001，16(3):220-227.

[8]LUCASC,TRZYNADLOWSRIAM.Combiningtheprinciplesofslidingmode,directtorquecontrol,andspace-vectormodula-tioninahigh-performancesensorlessACdrive[J].IEEETransactionsonIndustryApplications,2004,40(1):170-177.

[9]HASSANAA,SHEHATAEG.HighperformancedirecttorquecontrolschemesforanIPMSMdrive[J].ElectricPowersystemsResearch,89(2012)：171-182.

[10] 劉英培,栗然,梁宇超.基于雙滑模變結構PMSM直接轉矩控制無傳感器運行[J].電力自動化設備,2013,33(10):86-89.

[11]LIZheng,HUGuangda,CUIJiarui,etal.Sliding-modevariablestucturecontrolwithintegalactionforpermanentmagnetsynchronousmotor[J].ProceedingsoftheCSEE，2014(3):431-437.

[12] 鄭宏偉，饒益花，陳文光.三相電壓型PWM整流器的雙滑模控制方案研究[J].電源學報,2014(1):96-102.

[13] 張紅梅.電動汽車感應電機DTC轉矩與磁鏈變結構控制系統研究[D].長沙：湖南大學,2013.

[14] 王慶龍，張興，張崇巍.永磁同步電機矢量控制雙滑模模型參考自適應系統轉速辨識[J].中國電機工程學報,2014,34(6):897-902.

[13] 徐艷平，鐘彥儒.基于占空比控制的永磁同步電機新型直接轉矩控制策略[J].電工技術學報，2009,24(10)：27-32.

[14]INOUEY,MORIMOTOS,SANADAM.ExaminationandlinearizationoftorquecontrolsystemfordirectcontrolledIPMSM[J].IEEETransactionsonIndustryApplications，2010,46(1)：159-166.

[15] 顧德英，季正東，張平.基于SIMULINK的異步電機的建模與仿真[J].電力系統及其自動化學報,2003,15(2)：71-73.

[16] 佘致廷.感應電機無速度傳感器DTC參數辨識與控制方法的研究[D].長沙：湖南大學,2010.

Induction Motor DTC of Vector Subdivision Based on Sliding Mode Variable Structure

SHEZhi-ting,ZOUWei,XIONGKe-qin,TANQiong-qiong,LUWen-dou

(Hunan University,Changsha 410082,China)

In order to overcome torque ripple at low and switching frequency uncertainty of the tradition at direct torque control(DTC)，sliding mode variable structure DTC controller based on flux and torque was designed in the paper.The proposed controller is based on errors of flux and torque，rotor speed and stator current.On this basis,a control scheme with twelve voltage space vector DTC space vector modulation Instead of the hysteresis comparator and switching vector table was presented.Any required voltage space control vector could be synthesized using the subdivision twelve voltage space vectors.As such,the system can obtain more precise control of torque and flux,reduce torque ripple at low speed and ensure constant switching frequency of the inverter.Both computer simulation and experimental results are illustrated for verification.

induction motor; direct torque control; sliding mode variable structure; voltage space vector

2015-01-13

湖南省科技計劃項目(2013FJ4038)

TM346

A

1004-7018(2016)12-0087-06

佘致廷(1962-)，男，博士，副教授，研究方向為電力電子與電氣傳動。