基于虛擬加工的主軸跳動對表面粗糙度的作用規律分析

黃　強，王　利，翟江濤

(重慶理工大學， 重慶　400054)

?

引用格式：黃強，王利，翟江濤.基于虛擬加工的主軸跳動對表面粗糙度的作用規律分析[J].重慶理工大學學報(自然科學版)，2016(1):20-25.

Citation format：HUANG Qiang, WANG Li, ZHAI Jiang-tao.Rule Analysis of Spindle Runout Effected on Surface Roughness Based Virtual Processing[J].Journal of Chongqing University of Technology(Natural Science)，2016(1):20-25.

基于虛擬加工的主軸跳動對表面粗糙度的作用規律分析

黃強，王利，翟江濤

(重慶理工大學， 重慶400054)

摘要：機床主軸的跳動誤差是影響工件表面加工質量的重要因素，但其作用規律尚未被掌握。以車削外圓表面為例，提出了一種基于虛擬工件表面的粗糙度預測分析方法。首先，建立刀具模型和主軸跳動的數學模型，利用Matlab的計算與繪圖功能，得到在這2個因素作用下的虛擬工件表面；然后，利用高斯濾波原理對工件表面輪廓進行處理并得到粗糙度評定基準；最后，完成對表面粗糙度的數字化預測。采用這種方法，可以定量分析主軸跳動對表面粗糙度的作用規律。

關鍵詞：徑向跳動；虛擬加工表面；表面粗糙度；預測分析；高斯濾波

零件的表面粗糙度對產品的工作性能及可靠性等有著直接的影響。隨著工業技術的不斷發展，對加工精度及表面質量提出了更高的要求，相關研究工作也在不斷深入。目前，虛擬制造已成為現代制造技術的前沿領域[1]。天津大學等國內高校通過模擬數控加工仿真工件表面的形貌，開發了仿真平臺模擬整個加工過程，并利用回歸分析法預測了工件表面粗糙度[2-4]。在國外，也有學者通過回歸分析、正交實驗等數學方法和提取工件表面輪廓信息仿真表面形貌，建立工件表面粗糙度的預測模型，并達到了很好的預測精度[5-9]。表面粗糙度最常用的評定指標為表面輪廓的算術平均偏差，其表面輪廓中線的提取一般采用國際標準ISO16610[10]中推薦的高斯濾波原理。華中科技大學、哈爾濱理工大學等高校對高斯濾波原理在提取表面輪廓評定基準線的應用性及適用性方面進行了深入研究，為表面粗糙度的測量與評定提供了重要的理論支持[11-12]。研究并掌握表面粗糙度的影響因素及其作用規律是合理控制表面粗糙度的重要基礎。目前，對表面粗糙度的影響因素及其作用規律的量化分析仍主要依靠理論粗糙度公式，其包含的影響因素并未覆蓋主軸徑向跳動、進給運動誤差以及振動等重要因素。本文以探索機床主軸徑向跳動對表面粗糙度的影響規律為目標，研究其建模與分析方法。

1表面粗糙度及其影響因素

如圖1所示，工件表面的形貌按照其波動頻率可分為3個層次。低頻的是表面的形狀誤差(圖中未顯示)，中頻的稱之為波度，而表面粗糙度為高頻成分，指加工表面具有的較小間距和微小峰谷的不平度，屬于微觀幾何形狀誤差。表面粗糙度越小，則表面越光滑。表面粗糙度的影響因素眾多，至今沒有十分準確的分類描述。總體上看，工件的表面粗糙度取決于其加工工藝系統(工件本身、機床、夾具、刀具)，工藝參數(切削用量)，切削液以及加工環境。例如刀具角度與進給量、加工過程中刀具與零件表面間的摩擦情況、切屑分離時表面層金屬的塑性變形、工藝系統振動及環境振動等。

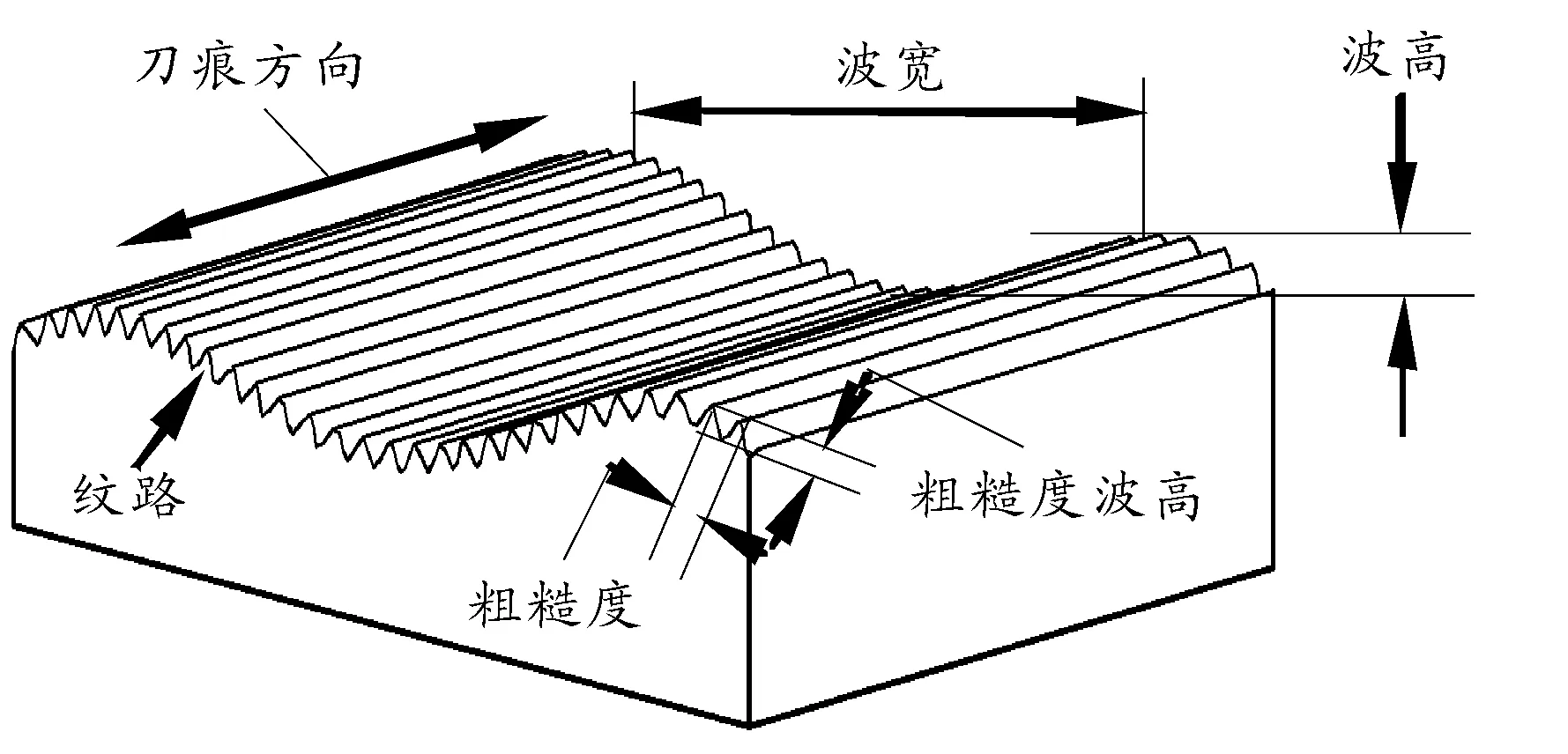
圖1　表面粗糙度示意圖

在上述影響因素中，目前只有刀具主副偏角(或刀尖半徑)、進給量與理論表面粗糙度的關系能夠量化表述，如圖2所示，其中o表示刀尖圓弧的圓心。在理想切削加工中，理論殘留高度Rmax可由式(1)計算。

(1)

式中：r表示刀尖圓弧半徑；f表示切削進給量。

式(1)又稱為理論粗糙度，而工件表面的實際粗糙度是在該理論粗糙度上疊加其他因素的作用而得到的。基于這一技術原則，本文研究機床主軸的徑向跳動對工件表面的影響程度，著重探索其建模與分析方法。

圖2　刀尖圓弧切削示意圖

2基于虛擬工件表面的粗糙度預測模型

2.1建立理想的虛擬工件表面

虛擬加工技術的產生和發展為研究表面粗糙度提供了新的技術途徑。利用虛擬加工，可以清晰描述工件表面的形成過程及結果(虛擬工件表面)。根據圖2所示要素之間的相對幾何位姿及運動關系，可得到車削圓柱表面的數學仿真模型。圖3、4是理想狀況下的車削虛擬工件表面。基本參數如下：刀具的進給量為0.1 mm/r；刀尖圓弧半徑為0.1 mm；主軸轉速為600 r/min；背吃刀量為0.03 mm。

圖3　理想的虛擬車削圓柱表面外觀

圖4　刀尖具圓弧半徑在工件表面的

2.2建立帶誤差的虛擬工件表面

2.2.1機床主軸回轉誤差建模

機床主軸的回轉精度是機床的一項重要精度指標。如圖5所示，車床主軸的回轉誤差主要包括主軸的徑向跳動誤差、軸向竄動誤差和主軸角度擺動誤差。在加工零件時，由于主軸的旋轉運動，在零件的徑向上會產生徑向跳動誤差，同時，在X軸和Y軸上會產生一定的角度擺動，在Z軸方向上會產生軸向的竄動誤差。

圖5　主軸回轉誤差示意圖

加工中，工藝系統的相對位姿、運動及其誤差可利用齊次坐標變換表示[13]。在坐標系的變換過程中，沿X，Y，Z軸的平移量設置為Δx(t)，Δy(t)，Δz(t)；繞X，Y，Z軸的轉動量設置為Δα(t)，Δβ(t)，Δγ(t)；ω表示主軸轉速；t表示主軸轉動時間；取運算符s代表sin，c代表cos；Tt表示純徑向跳動誤差矩陣；Tc表示純軸向竄動誤差矩陣；Tb表示純角度擺動矩陣。具體表示如下：

1) 主軸純徑向跳動的姿態矩陣：

(2)

2) 主軸純軸向竄動的姿態矩陣：

(3)

3) 主軸純角度擺動的姿態矩陣：

(4)

2.2.2建立帶誤差的虛擬工件表面

在現實的切削加工中，機床的誤差、變化的切削條件、機床的振動等都會影響工件的表面粗糙度。因此，殘留在工件表面的不僅是刀具軌跡留下的理論殘留高度，還有其他誤差因素導致的工件表面形貌的變化。在車削加工中，機床主軸的轉動直接帶動工件旋轉，在其他切削條件不變的情況下，主軸的3項回轉誤差直接影響著工件的表面粗糙度。本文著重探索粗糙度建模與分析的技術路線，故后續論述中均只考慮主軸徑向跳動的影響，即工件的表面粗糙度為加工表面理論殘留面積高度Rmax和機床主軸徑向跳動誤差Tt的疊加效果。將理想車削模型與式(2)所示的主軸回轉誤差矩陣相結合，利用Matlab計算和仿真出帶誤差的虛擬工件表面，如圖6、7所示。

圖6　帶誤差的虛擬車削圓柱面表面外觀

圖7　帶誤差的工件表面殘留高度局部放大圖

3虛擬加工表面的粗糙度預測方法

通過建模與仿真，刀具幾何參數、切削用量以及主軸徑向跳動對工件表面的影響均體現在圖6、7所示的虛擬工件表面中。在該表面上提取需要的表面輪廓數據，即可進行虛擬表面的粗糙度預測與評定。

3.1表面輪廓的數字化濾波及中線提取

表面粗糙度的評定需要按定義提取輪廓中線。該項工作的第1步是通過濾波方式去除檢測數據中的中低頻成分(形狀誤差和波度)。本文利用高斯濾波器[10]建立表面輪廓中線，濾波算法如下：

(5)

(6)

式中：h(x)表示高斯濾波器的權函數；h(λ)表示其頻率響應函數；λ表示波長；λc表示高斯濾波器的截止波長；α表示常數。高斯濾波器是一種具有線性相位的濾波器，當且僅當λ=λc時，其幅頻特性為50%，即濾波在截止波長處的通過率。因此，由式(6)可得α≈0.469 7。

表面粗糙度的評定基準線ω(x)可以表示為[14-15]：

(7)

(8)

式中：z(λ)是表面原始輪廓；r(x)表示粗糙度輪廓。

在實際測量或者軟件仿真過程中，其數據來自有限區域內的離散點。將式(7)進行離散化得：

(9)

(10)

式中：i=m,…,n-m；Zi-k=Z[(i-k)Δx]表示離散的數據點；hk為高斯濾波器的權函數的離散表示；m表示高斯函數的寬度；Δx表示數據點之間的間隔。

3.2去除邊界效應

在Matlab中編程實現輪廓中線的提取時，首先提取帶誤差的虛擬工件表面輪廓，并選取截止波長為0.8 mm；再根據高斯濾波器的定義，即式(7)～(9)得到實際表面輪廓及中線和粗糙度輪廓，如圖8、9所示。

圖8　工件的虛擬表面輪廓及中線

圖9　工件表面的粗糙度輪廓

在應用高斯濾波器時，采用離散的卷積或者是離散的傅里葉變換得到濾波中線，在其算法的實現過程中，會出現邊緣數據的失真。從圖8、9中可以看出：工件輪廓、中線和粗糙度輪廓的邊界都存在邊界效應，需要在首尾邊界處各去除一定長度的邊界數據之后才能對表面輪廓進行粗糙度的數字化預測。將邊界數據剔除之后得到的表面實際輪廓及中線和粗糙度輪廓如圖10、11所示。

圖10　去除邊界效應的工件表面及基準

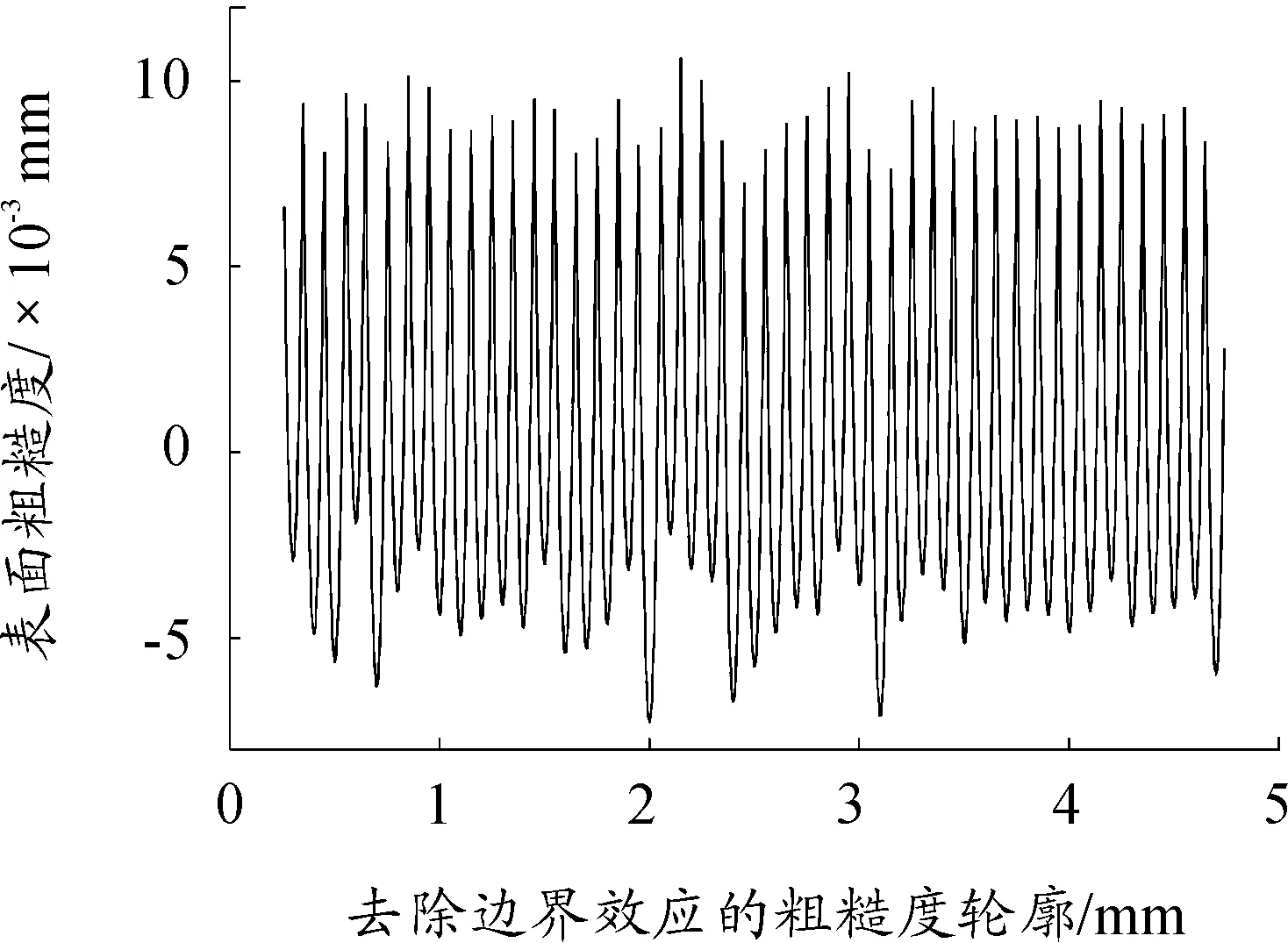
圖11　去除邊界效應的粗糙度輪廓

3.3表面粗糙度的評定

表面輪廓數據通過高斯濾波、中線提取及邊界數據剔除后，即可由定義對表面粗糙度進行評定與預測：

(11)

或者近似為

(12)

式中：lr是工件表面粗糙度輪廓的取樣長度；Z(x)是取樣長度內的縱坐標。

4主軸徑向跳動對表面粗糙度的作用規律分析

上述的建模與分析方法為研究表面粗糙度影響因素的作用規律提供了基礎。表1設計了20組不同的主軸徑向跳動范圍及其通過數字化預測得到的工件表面粗糙度值。其中，車削外圓的加工條件設置如下：進給量為0.1 mm/r，刀尖圓弧半徑為0.1 mm，主軸轉速為600 r/min，背吃刀量為0.03 mm。主軸徑向跳動的作用規律如圖12所示。

表1　不同主軸徑向跳動誤差對應的

續表

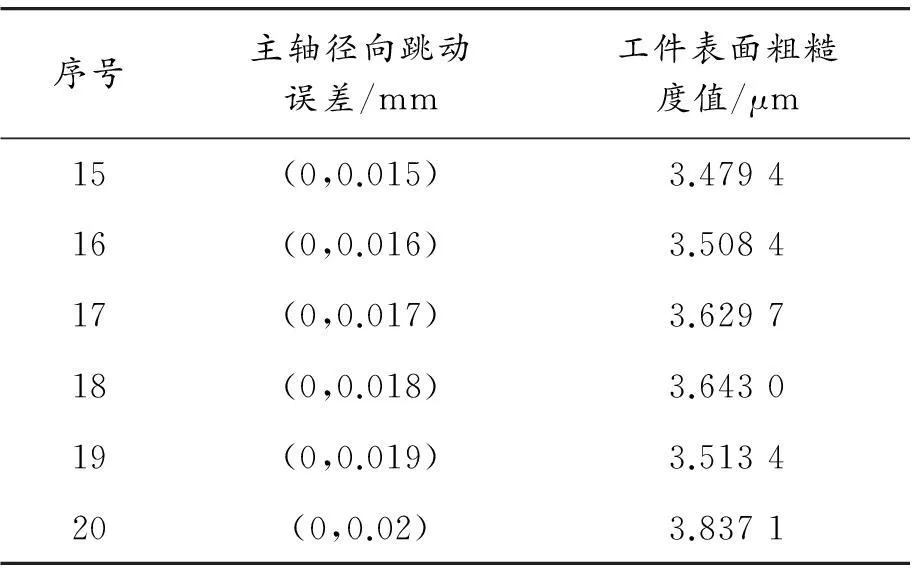
序號主軸徑向跳動誤差/mm工件表面粗糙度值/μm15(0,0.015)3.479416(0,0.016)3.508417(0,0.017)3.629718(0,0.018)3.643019(0,0.019)3.513420(0,0.02)3.8371

圖12　主軸徑向跳動誤差對工件表面

分析結果顯示：加工表面的粗糙度受機床主軸徑向跳動的影響，主軸徑向跳動誤差越大，工件表面粗糙度值越大，兩者之間呈非線性關系。利用兩者之間的量化對應關系，可以為表面粗糙度的控制，尤其是主軸徑向跳動的設計控制提供依據。

5結論

1) 通過零件表面成形原理的數字化建模，可以得到帶誤差的虛擬工件表面，并進行表面粗糙度的檢測和評定，為表面粗糙度影響因素的定量研究提供了基礎。

2) 機床主軸徑向跳動誤差越大，工件表面的粗糙度越大，兩者之間呈非線性關系。利用兩者之間的量化對應關系，可以為表面粗糙度的控制，尤其是主軸徑向跳動的設計控制提供依據。

參考文獻：

[1]楊國哲,王偉,鞏亞東,等.關于虛擬車削加工中的粗糙度預測的研究[J].組合機床與自動化加工技術,2004,01(3):11-13.

[2]王洪祥,李旦,董申.超精密車削表面租糙度預測模型的建立[J].高技術通訊,2003,5(15):77-81.

[3]范勝波.虛擬數控車削加工質量預測系統的研究[D].天津:天津大學,2005.

[4]張雪蓮,潘鐵強,汪建平,等.虛擬數控車削加工過程仿真與表面粗糙度預測[J].組合機床與自動化加工技術,2009,6(4):82-83.

[5]MITAL A,MEHTA M.Surface finish prediction models for fine turning[J].The International Journal Of Production Research,1988,26(12):1861-1876.

[6]ELBARADIE M A.Computer aided analysis of a surface roughness model for turning[J].Journal of Materials Processing Technology,1991,26(2):207-216.

[7]JACK C X,WANG X.Development of Empirical Models for Surface Roughness Prediction in Finish Turning[J].International Journal of Advanced Manufacture Technology,2002,256(34):348-356.

[8]PATRIKAR R M.Modeling and simulation of surface roughness[J].Applied Surface Science,2004,228(1):213-220.

[9]CHENG J,GONG Y,WANG J.Modeling and evaluating of surface roughness prediction in micro-grinding on soda-lime glass considering tool characterization[J].Chinese Journal of Mechanical Engineering,2013,26(6):1091-1100.

[10]ISO16610—2006.Geometrical product specifications(GPS)-Filtration-Part1:Overview and basic concept[S].

[11]曾文涵,謝鐵邦,蔣向前,等.表面粗糙度的穩健提取方法研究[J].中國機械工程,2004,15(2):35-38.

[12]許景波,袁怡寶,崔曉萌,等.表面測量中高斯濾波中線的有理逼近實現[J].吉林大學學報(工學版),2014,44(5):1347-1352.

[13]魏坤.機床主軸回轉精度的數字化建模與分析方法[D].重慶:重慶理工大學,2013.

[14]唐焱,劉棟,侯原亮，等.基于Matlab GUI的表面粗糙度評定算法的實現[J].機械設計與研究,2012,28(5):52-55.

[15]徐衛東,任小洪,周天鵬,等.基于 Matlab-GUI 數控機床熱誤差補償的仿真系統[J].重慶理工大學學報(自然科學版),2011,25(3):39-42.

(責任編輯陳艷)

Rule Analysis of Spindle Runout Effected on Surface Roughness

Based Virtual Processing

HUANG Qiang, WANG Li, ZHAI Jiang-tao

(Chongqing University of Technology, Chongqing 400054, China)

Abstract:The spindle runout is an significant factor affecting the surface quality of workpiece, but its action rule has not been mastered now. Taking the turning cylinder surface as an example, an forecast analysis way of surface roughness based on the virtual workpiece surface was proposed. The mathematical model included tool and spindle runout was established at the first. Using the calculating and plotting of MATLAB, the virtual surface affected by this two factors was built. Using the Gauss filter principle to deal with this surface, and the evaluation criteria of surface roughness was obtained. At last, the digital prediction of surface roughness was achieved. By this method, the quantitative rule of the spindle runout affecting surface roughness may be analyzed.

Key words:runout; virtual processing surface; surface roughness; prediction analysis; Gauss filter

文章編號：1674-8425(2016)01-0020-06

中圖分類號：TG506.1

文獻標識碼：A

doi:10.3969/j.issn.1674-8425(z).2016.01.004

作者簡介：黃強(1966—)，男，河南人，教授，主要從事機械制造裝備、數字化設計與制造研究。

基金項目：國家自然科學基金資助項目(51075419)

收稿日期：2015-10-15