基于改進蜂群算法的數字信號調制識別

吳少華，單劍鋒

(南京郵電大學 電子科學與工程學院，江蘇 南京 210000)

基于改進蜂群算法的數字信號調制識別

吳少華，單劍鋒

(南京郵電大學 電子科學與工程學院，江蘇 南京 210000)

針對傳統人工蜂群(ABC)算法初始種群在解空間分布不均勻、收斂速度慢等缺點，文中提出一種基于二維均勻設計和歐氏距離的改進蜂群算法。改進蜂群算法在構造初始食物源時采用二維均勻設計使食物源在解空間均勻分布，提高了算法的全局搜索能力；在構造新食物源時采用歐氏距離法提高了算法的尋優效率。文中利用信號二階以上累積量可以抑制噪聲影響的特性，從二階、四階和六階累積量中提取四個特征參數作為特征向量，采用支持向量機分類器，并用改進蜂群算法對支持向量機的懲罰因子和核函數參數進行優化，實現了2FSK、BPSK、QPSK、16QAM、64QAM五種調制方式的分類識別。仿真結果表明，改進蜂群算法具有更快的收斂速度，且改進ABC-SVM方法在信噪比-3 dB時具有更好的識別效果，平均識別率為92.9%；當信噪比超過4 dB時，改進ABC-SVM方法平均識別率達到99%。

人工蜂群；歐氏距離；二維均勻設計；支持向量機；調制識別

0 引 言

隨著通信技術和國民經濟的發展，數字信號的自動識別在民用和軍事領域被廣泛應用。在日趨復雜通信環境中，通信信號調制方式的識別仍是認知無線電、頻譜監測與管理、通信對抗等領域的重要研究課題。

通信信號的調制識別方法主要分為兩大類：判決理論識別方法和統計模式識別方法。前者采用概率論和假設檢驗理論來解決信號分類問題；后者首先將接收信號映射到特征域，然后利用模式識別方法確定判決域。統計模式識別方法主要分為兩個部分：特征提取和分類器。對于特征提取，目前主要采用的方法有提取信號瞬時頻率、瞬時相位以及功率譜密度、小波變換、原點矩、累積量等方法[1-4]。對于分類器，支持向量機(Support Vector Machines,SVM)分類器由于其能有效解決小樣本、高維數及局部最優等問題而被廣泛采用。

人工蜂群(Artificial Bee Colony,ABC)算法是一種基于蜜蜂種群智能行為的優化算法，由Karaboga在2005年提出。算法簡單易用、控制參數少、魯棒性強，適用于對復雜優化問題進行求解[5]。文獻[6]將人工蜂群算法應用于支持向量參數的優化，與粒子群算法和遺傳算法進行了比較，獲得更高的分類準確率。文獻[7]將蜂群算法與支持向量機相結合，在實測軸承故障信號的識別中獲得99.1%的準確率。然而，傳統的人工蜂群算法仍存在著種群多樣性差、搜索速度慢、易陷入局部最優等缺陷。文獻[8]引入小生境技術，解決了人工蜂群算法早熟收斂、搜索速度較慢等問題。文獻[9]將混沌思想引入ABC算法中，利用混沌的隨機性和遍歷性提高算法的全局搜索能力。文獻[10]引入OBL策略產生新食物源取代每次迭代的最差食物源,并結合NIT技術提出一種多峰優化方法。

文中采用人工蜂群算法對支持向量的參數進行優化，并結合支持向量機所需優化參數為兩個的事實，對人工蜂群算法進行改進。在種群初始時，采用二維均勻設計理論，使初始食物源更均勻分布在解搜索空間；在構建新食物源時，提出一種基于歐氏距離的覓食方法以改進種群局部和全局的更新策略。

1 信號和特征提取

文中研究的信號的調制方式分別是2FSK、BPSK、QPSK、16QAM、64QAM。考慮到信號的高階累積量包含了信號的調制信息，且二階以上的累積量能消除高斯噪聲的影響，具有良好的抗噪聲能力，因此文中以二階、四階和六階累積量為基礎進行特征提取。

1.1 信號模型

設接收信號的模型為：

式中，k=1,2,…,N，N為發送碼元序列的長度；ak為發送碼元序列；x(t)為發送碼元波形；Ts為碼元寬度；fc為載波頻率；θc為載波相位；E為信號能量；n(t)是與發送信號s(t)獨立的零均值的復高斯白噪聲。

1.2 高階累積量

k階平穩隨機過程{x(t)}的k階累積量定義為[11]：

Ckx(τ1,τ2,…,τk-1)=

Cum(x(t),x(t+τ1),…,x(t+τk-1))

(2)

對于一個零均值的復平穩隨機工程X(t)，定義p階混合矩為：

Mpq=E{[X(t)]p-q[X*(t)]q}

(3)

式中，*表示函數的共軛。

定義其各階累積量為：

C20=Cum(X,X)=M20=E{[X(t)]2}

(4)

C21=Cum(X,X*)=M21=E[X(t)X*(t)]

(5)

C40=Cum(X,X,X,X)=M40-3(M20)2

(6)

C41=Cum(X,X,X,X*)=M41-3M20M21

(7)

C42=Cum(X,X,X*,X*)= M42-|M20|2-2(M21)2

(8)

C60=Cum(X,X,X,X,X,X)= M60-15M20M40+30(M20)3

(9)

C63=Cum(X,X,X,X*,X*,X*)=M63-6M20M41-9M42M21+18(M20)2M21+12(M21)3

(10)

對于接收信號r(t)=s(t)+n(t)，其中s(t)為發送信號，n(t)為零均值的復高斯白噪聲，s(t)與n(t)相互獨立。由累積量的性質有：

Cum(r(t))=Cum(s(t))+Cum(n(t))

(11)

由式(4)～(10)知，零均值高斯白噪聲大于二階的累積量值為零，則接收信號的累計量可寫成：Cum(r(t))=Cum(s(t))。

由此可知，接收信號的高階累積量等于發送信號的高階累積量，從而不受高斯白噪聲的影響。用式(3)～(10)采用文獻[12]的方法計算數字調制信號的高階累積量。設信號的能量為E，則數字調制信號高階累積量的理論值如表1所示。

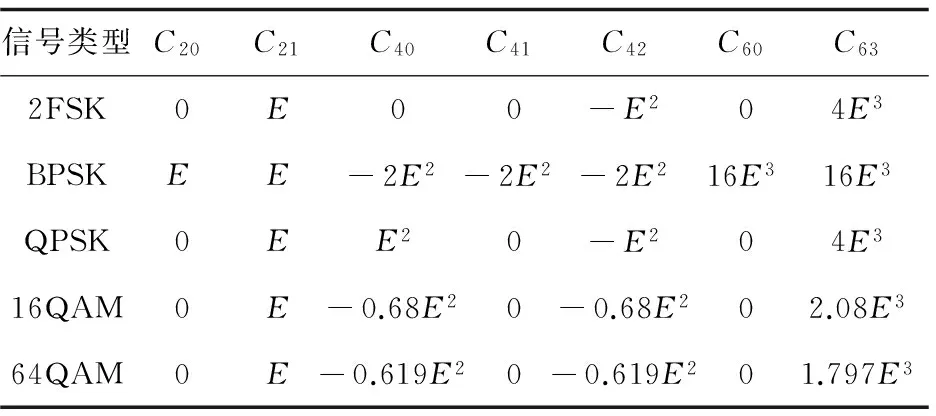
表1 數字調制信號高階累積量的理論值

因為歸一化后能夠提高SVM分類精度且能避免噪聲和接收信號的功率對識別的影響，文中構建如下歸一化特征量：

由上可知，利用F1特征量，可以識別出BPSK；利用F2特征量，可以識別出2FSK；結合F3和F4特征量，可以識別出QPSK、16QAM、64QAM。因此構建特征向量[F1,F2,F3,F4]。

2 改進ABC算法優化的支持向量機分類器

2.1 支持向量機原理

支持向量機(SVM)就是尋找一個最優線性分類平面，即最大間隔超平面。當訓練集為非線性時，將其映射到高維線性特征空間，在高維空間中構造最優線性分類超平面[13-15]。

對于文中情況，因為是五種調制信號的識別，設訓練樣本集為：

(x1,y1),…,(xi,yi),(i=1,2,…,n),x∈Rn,y∈{1,2,3,4,5}

式中，n為樣本數量；xi為特征向量；yi為類別標簽。

數字信號的調制識別是一種復雜的模式識別問題，不能簡單地假設成線性可分，考慮訓練集為線性不可分的，優化函數為：

(12)

s.t.,αi≥0,i=1,2,…,n

那么問題的最優決策函數為：

(13)

式中，K(xi,xj)為核函數。

文中采取高斯核函數[16]：

支持向量機分類性能主要依賴于懲罰因子C以及核函數K(xi,xj)參數γ。懲罰因子C越大，對誤分類的懲罰越大，核參數影響樣本在高維特征空間的分布情況。因此采用人工蜂群算法對懲罰因子以及核參數進行優化能獲得較好的識別率。

2.2 傳統人工蜂群算法原理

人工蜂群(ABC)算法模擬自然界蜜蜂采蜜的過程，將蜜蜂分為三種不同的工種：采蜜蜂、觀察蜂和偵查蜂[17-18]。采蜜蜂和觀察蜂的數量各占蜜蜂全體數量的一半。食物源與采蜜蜂數量相等且一一對應。如果某個食物源被采蜜蜂和觀察蜂放棄，則該食物源對應的采蜜蜂變為偵查蜂。人工蜂群的搜索活動可概括如下：采蜜蜂根據記憶中的食物源位置在其鄰域內確定一個新的食物源；采蜜蜂在回到蜂巢后將它們的食物源信息通過舞蹈與觀察蜂共享，觀察蜂根據采蜜蜂傳回的信息對食物源進行優選；觀察蜂根據選擇的食物源在其鄰域內搜索一個新的食物源；放棄食物源的采蜜蜂變為偵查蜂并開始搜索一個新的隨機食物源。

2.3 基于二維均勻設計方法的種群初始化

ABC算法對種群初始構造較為敏感，初始食物源在搜索空間分布不均勻將導致算法的搜索范圍受到限制，影響算法的全局搜索能力。用二維均勻設計方法構造初始食物源可以在盡可能少的迭代次數內達到實驗要求的精度，從而加速算法的收斂。

在ABC算法中，每個食物源的位置代表優化問題的一個可能解，每個解xi(i=1,2,…,SN)是一個D維向量，D為優化參數的個數，每個食物源的花蜜量對應每個解的適應度。

文中的解向量(C,γ)是二維向量，其中懲罰因子C的搜索范圍為[1,100]，核參數γ的搜索范圍為[0,0.1]。將C的搜索范圍分成均勻五段，分別為[1,20],[20,40],[40,60],[60,80],[80,100]；將γ的搜索范圍也分成均勻五段，分別為[0,0.02],[0.02,0.04],[0.04,0.06],[0.06,0.08],[0.08,0.1]。然后，分別以C為橫坐標，γ為縱坐標，構建二維平面坐標系，如圖1所示。

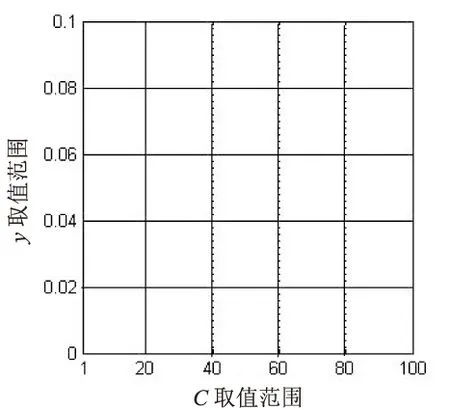
圖1 初始食物源的構建范圍示意圖

圖1中每一個方格代表一個解向量的初始構建范圍，分別從25個范圍中各構建一個解向量作為種群的初始食物源。

2.4 基于歐氏距離的食物源構造方法

在傳統的人工蜂群算法中，新食物源的生成公式如下：

vij=xij+φij(xij-xkj)

(15)

式中，k∈{1,2,…,SN}，j∈{1,2,…,D}是隨機選擇的下標，并滿足k≠i；φij為[-1,1]之間的隨機數。

由式(15)可以看出，蜜蜂搜尋新解的范圍有可能是整個解空間，這使蜜蜂的搜索行為存在盲目性，影響算法尋優效率。

文中提出一種基于歐氏距離的食物源構造方法。在二維平面中，歐氏距離是指兩點之間的距離。文中設有食物源(C1,γ1)和(C2,γ2)，定義食物源間的歐氏距離為：

(16)

每一次的迭代過程中，可以得到本次迭代過程中的最優解xbest，那么可以計算出每個解與最優解間的歐氏距離，距離越大，搜索新解的范圍就越大，反之，搜索范圍越小。

由圖1可知，全局最大歐氏距離為兩頂點(1,0)和(100,0.1)間距離，定義權重值Δi，如下：

(17)

則食物源的生成公式改進如下：

vij=xij+Δi·φij(xij-xkj)

(18)

2.5 改進人工蜂群算法優化支持向量機參數過程

改進人工蜂群算法優化SVM參數方法描述如下：

步驟一：初始化人工蜂群算法的參數，包括蜜蜂種群的數量、食物源的數量、控制參數limit、最大迭代次數N、SVM參數(C,γ)的范圍。

步驟二：將(C,γ)作為ABC算法的解向量，即食物源。根據二維均勻方法在(C,γ)的范圍內生成初始食物源(解)，將每個食物源(解)代入SVM計算出識別率，作為適應度。

步驟三：采蜜蜂在每個初始食物源(解)的附近由式(18)生成新的食物源(解)并計算適應度，與初始食物源(解)的適應度進行比較，保留適應度較高的食物源(解)。

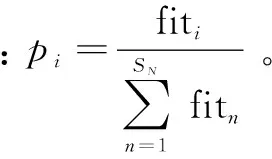
步驟五：計算每個食物源(解)的尋優次數是否超過控制參數，若超過控制參數，表示該食物源(解)陷入局部最優，舍棄該食物源(解)，該采蜜蜂變成偵查蜂，由式(18)尋找出新的食物源。

步驟六：若ABC算法達到最大迭代次數，則轉至步驟七，否則，轉至步驟三。

步驟七：結束ABC訓練，輸出最優解(C,γ)。

3 仿真結果及分析

為了驗證改進ABC算法優化SVM參數能有效地提高調制信號的識別率，在計算機中進行仿真實驗。實驗平臺為MATLAB7.9，安裝libsvm工具箱[19]。信號載波頻率fc為2 000Hz，采樣頻率fs為12 000Hz，碼元速率fb為500bps，2FSK的頻偏為750Hz。信道模型為零均值的高斯白噪聲信道。

人工蜂群算法參數具體設置：種群大小為50，食物源大小為25，最大迭代次數為200，控制參數limit為30，懲罰因子C的搜索范圍為[1,100]，核參數γ的搜索范圍為[0,0.1]，適應度為(C,γ)代入SVM分類器計算出的識別率。SVM訓練樣本集大小為500，其中各調制信號的特征向量分別為100組，共進行100次蒙特卡洛實驗。

3.1 進化曲線對比

圖2、圖3分別為ABC和改進ABC算法在-3 dB和6 dB時的平均進化曲線。

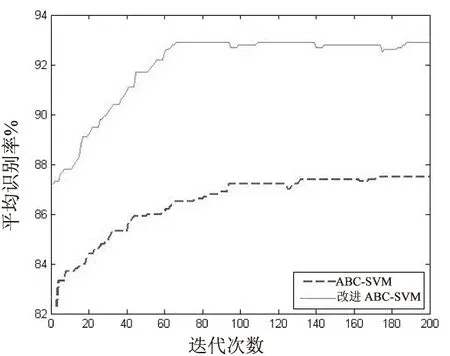
圖2 ABC-SVM、改進ABC-SVM在-3 dB下的進化曲線

圖3 ABC-SVM、改進ABC-SVM在6 dB下的進化曲線

從圖中可以看出，改進ABC算法具有更快的全局收斂速度和更好的全局尋優能力。從圖2可以看出，改進ABC算法與ABC算法最終收斂的識別率不同，改進ABC算法在93%附近收斂，而傳統ABC算法在88%附近收斂，因此在低信噪比的條件下，改進ABC算法有更好的平均識別率。

3.2 識別率對比

圖4為ABC-SVM、改進ABC-SVM在各個信噪比條件下的識別率。

從圖4可以看出：當信噪比在-3 dB以上時，ABC-SVM算法平均識別率在87%以上，改進ABC-SVM算法識別率在92%以上；當信噪比超過6 dB時，平均識別率均達到99%。由此可見，ABC算法優化的SVM在調制信號的識別中能取得較好的平均識別率，而改進ABC算法在低信噪比下的識別率優于傳統ABC算法。在當今日趨復雜的信號環境中，特別在軍事對抗中，信號的傳輸條件非常差。文中提出的改進ABC算法優化支持向量機參數的方法在信噪比較低的情況下有較好的識別率，當信噪比為-3 dB時，平均識別率為92.9%。因此，文中方法在調制識別的現實應用中能取得較為理想的效果。

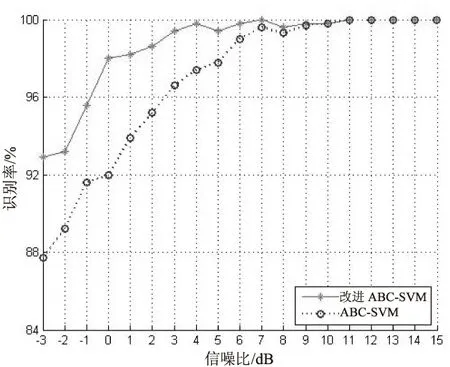
圖4 ABC-SVM、改進ABC-SVM在不同信噪比下的平均識別率

4 結束語

文中通過調制信號的高階累積量構建特征向量，提出采用改進人工蜂群算法優化SVM模型中的懲罰因子和核函數參數的方法，實現了對調制信號的分類識別。針對傳統ABC算法中存在的初始種群在解空間分布不均，算法搜索慢和算法收斂慢的缺點，文中提出基于二維均勻設計的初始解構造方法和基于歐氏距離的新食物源構造方法，一定程度上加快了算法的搜索速度和收斂速度。仿真結果表明，人工蜂群算法優化后的SVM模型對調制信號的識別有較高的準確率，在高信噪比的條件下平均識別率接近100%。而改進人工蜂群算法不僅有更好的收斂速度，而且在低信噪比條件下也有近93%的識別率。

人工蜂群算法提出的時間還不長，仍處于起步階段，對其理論和應用的研究空間還很大，還需要進一步的研究。在后續的工作中，筆者將會對蜂群算法的尋優過程進一步優化，并將其應用于調制信號的識別研究。

[1] Su W,Xu J L,Zhou M C.Real-time modulation classification based on maximum likelihood[J].IEEE Communications Letters,2008,12(11):801-803.

[2] Li Y,Wang F,Zhu G.Hybrid digital modulation classification[C]//Proc of 8th international wireless communications and mobile computing conference.[s.l.]:IEEE,2012.

[3] 王玉娥,張天騏,白 娟,等.基于粒子群支持向量機的通信信號調制識別算法[J].電視技術,2011,35(23):106-110.

[4] Orlic V D,Dukic M L.Automatic modulation classification:sixth-order cumulant features as a solution for real-world challenges[C]//Proc of telecommunications forum.[s.l.]:IEEE,2012:392-399.

[5] Zhang C Q,Zheng J G,Wang X.Overview of research on bee colony algorithms[J].Application Research of Computers,2011,28(9):3201-3204.

[6] 于 明,艾月喬.基于人工蜂群算法的支持向量機參數優化及應用[J].光電子·激光,2012,23(2):374-378.

[7] 劉 路,王太勇.基于人工蜂群算法的支持向量機優化[J].天津大學學報,2011,44(9):803-809.

[8] 臧明相,馬 軒,段奕明.一種改進的人工蜂群算法[J].西安電子科技大學學報,2015,42(2):65-70.

[9] 羅 鈞,李 研.具有混沌搜索策略的蜂群優化算法[J].控制與決策,2010,25(12):1913-1916.

[10] 畢曉君,王艷嬌.改進人工蜂群算法[J].哈爾濱工程大學學報,2012,33(1):117-123.

[11] 張賢達.現代信號處理[M].第2版.北京:清華大學出版社,2002:263-274.

[12] Ho K C,Prokopiw W,Chan Y T.Modulation identification of digital signals by the wavelet transform[J].IEE Proceedings - Radar,Sonar and Navigation,2000,147(4):169-176.

[13] 王建勇,王 海.基于高階累積量和SVM的OFDM調制制式識別[J].計算機與數字工程,2008,36(6):41-44.

[14] 張學工.關于統計學習理論與支持向量機[J].自動化學報,2000,26(1):32-42.

[15] 孫建成,張太鎰,劉海員.基于SVM的多類模擬調制方式識別算法[J].電子科技大學學報,2006,35(2):149-152.

[16] 杜樹新,吳鐵軍.模式識別中的支持向量機方法[J].浙江大學學報：工學版,2003,37(5):521-527.

[17] Karaboga D,Basturk B.A powerful and efficient algorithm for numerical function optimization: artificial bee colony (ABC) algorithm[J].Journal of Global Optimization,2007,39(3):459-471.

[18] Karaboga D,Basturk B.On the performance of artificial bee colony (ABC) algorithm[J].Applied Soft Computing,2007,8(1):687-697.

[19] Chang C C,Lin C J.LIBSVM:a library for support vector machines[J].ACM Transactions on Intelligent Systems & Technology,2001,2(3):389-396.

A Modulation Identification Algorithm for Digital Signals Based on Modified Artificial Bee Colony Algorithm

WU Shao-hua,SHAN Jian-feng

(School of Electronic Science and Engineering,Nanjing University of Posts and Telecommunications,Nanjing 210000,China)

In view of the slow convergence speed and non-uniform distribution of the initial food source of traditional Artificial Bee Colony (ABC) algorithm,a modified ABC algorithm based on two-dimensional uniform design and Euclidean-distance has been proposed.Two-dimensional uniform design is used to make the food source uniformly distribute in the solution space when the modified ABC algorithm establishes the food source,which can improve the global search ability of the algorithm.Euclidean-distance is applied in constructing new food source to improve the efficiency optimization.In this paper,four feature parameters which are picked up from second-order,fourth-order and sixth-order cumulants are obtained as a feature vector because second and higher order cumulants can suppress additive white Gaussian noise.SVM classifier and modified ABC algorithm is used to optimize the penalty factor and kernel function parameter,realizing the identification of 2FSK,BPSK,QPSK,16QAM and 64QAM.The simulation results show that the convergence speed of modified ABC algorithm is improved and the average recognition rate is 92.9% when SNR is -3 dB,as well as over 99% when SNR is more than 4 dB.

artificial bee colony;Euclidean-distance;two-dimensional uniform design;support vector machines;modulation identification

2015-09-18

2015-12-22

時間：2016-05-25

國家自然科學基金資助項目(61302155，GZ212015)

吳少華(1990-)，男，碩士生，研究方向為調制信號識別與分類；單劍鋒，副教授，博士，研究方向為智能信息處理、調制信號識別、電路故障診斷等。

http://www.cnki.net/kcms/detail/61.1450.TP.20160525.1709.056.html

TP911

A

1673-629X(2016)07-0046-05

10.3969/j.issn.1673-629X.2016.07.010