基于隨機幾何理論的多小區協作網絡分析

蔡 杰，劉 陳，陸 峰

(南京郵電大學 電子科學與工程學院，江蘇 南京 210046)

基于隨機幾何理論的多小區協作網絡分析

蔡 杰，劉 陳，陸 峰

(南京郵電大學 電子科學與工程學院，江蘇 南京 210046)

多小區協作技術能夠解決擁堵蜂窩網絡中小區邊緣用戶通信質量較差的問題,但是目前維納模型無法準確分析該技術對蜂窩網絡的影響。所以為了合理分析多小區協作技術帶來的性能提升，文中提出利用泊松點過程的方法對蜂窩小區進行建模。在該模型下利用隨機幾何工具，分析了下行鏈路和上行鏈路中使用多小區協作技術情況下的覆蓋概率，得到了覆蓋概率準確數學表達式和該技術所能提供的增益。通過分析發現，使用多小區協作技術能明顯提升小區的覆蓋能力。并且隨著協作越充分，該技術帶來的增益越大。

蜂窩網絡；多小區協作；泊松點過程；覆蓋概率；隨機幾何

1 概 述

現代社會手機用戶數量爆發式的增長使得各蜂窩網絡中的上行鏈路和下行鏈路信道堵塞。這種情況下，蜂窩小區的小區內部及小區間干擾就成為了制約整個無線通信網絡吞吐量的重要因素。因此如何制約和減輕干擾信號對手機用戶通話質量的影響就成為了設計新一代無線通信系統的重要因素。

多小區協作技術允許多個基站同時為一個用戶提供服務，從而抑制干擾信號、提高通信質量。但是這種質量的提高需要消耗大量網絡資源，這些基站組要通過光纖或者其他反饋鏈路將來自同一個用戶的信號傳給數據中心進行進一步的處理[1]。所以考慮到網絡資源和數據處理能力的消耗，多小區協作并不適合廣泛應用于整個空間中的所有用戶。在現實情況中，由于手機終端設備發送功率的不斷提高和信號編碼技術的應用，處于小區中間的普通用戶通話質量能夠得到保障，但是考慮到處于小區邊界的手機用戶距離周圍基站較遠，信道狀況較為惡劣，其通話質量受到干擾信號的影響較大。所以為了改善這一情況，處于小區邊緣位置的用戶可以使用多小區協作技術。因此文中的分析對象是蜂窩小區的邊緣用戶[2]。

基于以上假設，對于下行鏈路中某小區邊緣用戶，它能同時接到來自這n個服務基站的有用信號。而在上行鏈路中，該用戶能夠將信號同時發送給這n個服務基站。

近年來，多小區協作技術被廣泛研究。但大部分論文均使用在分析通信系統中最常用的維納模型(Wynermodel)對整個蜂窩網絡進行建模。例如，文獻[3-7]就利用維納模型對在下行鏈路中使用多小區協作技術進行了詳細分析。

維納模型是一個易于分析但是過于理想化的模型。維納模型中，認為用戶到基站之間的信道為理想信道，小區內干擾是一個常數，而小區間干擾可以忽略不計。但是在現實情況中，由于空間中的手機用戶增多導致小區間的信號干擾增加，所以小區間干擾不能忽略不計。而且隨著空間中手機用戶密集程度的變化，小區內部的干擾也會產生變化，所以將小區內干擾信號假設成常數也是過分理想化了。維納模型的另一個缺陷是，它假設空間中的所有蜂窩都是嚴格的正六邊形或矩形。但是在實際情況中蜂窩小區的形狀卻是隨機的。所以傳統的維納模型不再適合分析現代復雜的無線通信系統[8-9]。

由于維納模型眾多缺陷的存在，使得很多研究者開始使用隨機幾何模型來描述現代通信網絡的拓撲結構。隨機幾何模型認為空間中的所有基站和用戶都是隨機分布的，這樣就能很好地符合當代手機用戶隨機分布于整個空間中的實際情況。文獻[10-12]使用隨機幾何模型分析隨機選擇的某小區邊緣用戶在上行鏈路和下行鏈路中獲得的信干比時，利用現代隨機幾何理論提供的一系列有效工具得到相比于維納模型更簡潔且更精確的分析結果。

由于文中的目標是為了能夠更加準確地分析出對于某個使用多小區協作技術的小區邊緣用戶，在上行鏈路和下行鏈路的通話質量。所以選擇了隨機幾何理論中的泊松點過程模型進行建模和分析，并且使用文中提出的根據小區邊緣用戶的位置動態選擇協作基站的策略，在不限定協作基站數目的情況下，得到了上行鏈路和下行鏈路的覆蓋概率通用數學表達式。

2 下行鏈路

在蜂窩網絡的下行鏈路中，假設整個空間中的基站(BSs)分布服從強度為λd的泊松點過程(PPP)Φd。對于一個隨機選擇的小區邊緣用戶，由于文中分析的場景為整個平面，所以可以不失一般性地認為該用戶處在平面的原點位置。將下行鏈路覆蓋概率定義為，某用戶收到的有用信號功率和干擾信號功率比值(Signal-to-InterferenceRatio，SIR)大于某個門限值概率。其數學表達式可以寫為：

(1)

其中,Pd代表用戶收到的有用信號功率;Ij代表用戶收到的干擾信號功率;T代表門限值。

2.1 下行鏈路多小區協作系統模型

對于下行鏈路信道，使用文獻[12]提出的標準功率衰落模型對其進行建模。在下行鏈路中，定義路徑衰落指數為α(α>2)。對于第i個服務基站到處于原點的用戶之間的距離用Ri表示。由于文中使用的模型中基站位置是隨機分布的，所以Ri為隨機變量。假設對于基站和特定用戶之間的信號傳輸只受到均值為1的瑞利衰落的影響。所有基站的發送功率持續且穩定，并且基站發送功率的均值為1/μ。

根據之前的假設可知，對于特定的小區邊緣用戶來說，他收到的有用信號功率是其收到的來自于距離其最近的n個基站信號功率的線性疊加[13]，所以該用戶收到的有用信號功率的表達式為:

(2)

而其收到的干擾信號就是來自于空間中所有的干擾基站[14]，所以干擾信號功率的表達式為：

(3)

其中，Rn表示最遠的第n個服務基站到位于原點的特定用戶之間的距離；β(0,Rn)表示以原點為圓心、Rn為半徑的圓域。可以認為在β(0,Rn)之外的點距離原點的距離均大于Rn，所以Φβ(0,rn)這個點集內的點j代表的是干擾基站的位置。參數Dj代表處在j點位置上的干擾基站到原點用戶的距離。

又根據泊松點過程的性質可知，在某個點集中刪去有限個點后，該點集仍服從泊松點分布，所以Φβ(0,rn)這個點集仍服從泊松點過程分布。根據下行鏈路覆蓋概率定義，可以得到其數學表達式為：

又根據帕斯瓦爾定理可知：

P[pd>(IrT)]=

(5)

其中，符號L表示對隨機變量求拉普拉斯變換。

由式(4)、(5)可知，上行鏈路覆蓋概率是由用戶到各服務基站之間距離Ri的概率密度函數fRi(rt)，以及用戶收到的有用信號功率和干擾信號功率的拉普拉斯變換這兩個參數所決定。下兩節將分別計算這兩個參數。

2.2 服務基站和用戶之間距離的概率密度函數

根據前面的分析可知，用戶所選擇的服務基站是距其最近的n個基站，而隨機變量Ri則是描述第i個服務基站到目標用戶之間的距離。那么根據分布函數的定義可知，隨機變量Ri的分布函數表達式為：

FRi(r)=P{Rir}

P{Ri>r}=

P{在圓域β(0,r)中至多只有i-1個點}=

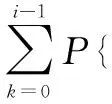
其中，Λ(r)代表泊松點過程在圓域β(0,r)內點分布強度的度量。

根據泊松點過程的定義，其表達式為：

所以根據概率密度函數定義，可得到某特定用戶到第i個服務基站距離的概率密度函數表達式為：

2.3 干擾信號與有用信號功率的拉普拉斯變換

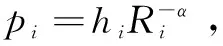
(7)

又根據拉普拉斯變換的性質可得隨機變量pi的拉普拉斯變換為：

Fpi(s)=

(8)

對于用戶來說，其收到的有用信號的功率為來自各基站信號功率的線性疊加：

同時又由于pi是獨立隨機變量，根據卷積定理可以得到隨機變量Pd的概率分布函數為:

fpd(x)=fp1(x)*fp2(x)*…*fpi(x)*…*fpn(x)

由此，根據拉普拉斯變換的定義可知：

(9)

下行鏈路中小區間干擾信號功率Ir的拉普拉斯變換根據

文獻[12]可知：

(10)

將式(6)、(9)、(10)帶入式(4)便可得到下行鏈路覆蓋概率的數學表達式。

3 上行鏈路

3.1 上行鏈路系統模型

在上行鏈路中，某隨機選擇的小區邊緣用戶能夠將信號發送給距其最近的n個基站。為了便于分析，定義對于使用多小區協作技術的小區邊緣用戶上行鏈路，該用戶將信號同時發送給n個基站，這n個基站中至少有m(1≤m≤n)個收到的來自該用戶的信號功率和該基站收到的干擾信號功率之比(SIR)大于某一門限時，就認為該用戶的上行鏈路被覆蓋。

同時對于上行鏈路來說，手機的發送功率受到本身硬件的制約，所以上行鏈路的發送功率控制是分析覆蓋概率必不可少的考慮因素。文中認為手機的發送功率與該手機距目標基站之間的距離成正比，比例常數為k。因此可以認為對于距離越近的目標基站，手機的上行鏈路發送功率越小。

在多小區協作中，考慮小區邊緣用戶所處的信道條件較差。所以為了保證上行鏈路的通信質量最好，假設手機的發送功率是由用戶到距其最遠的第n服務基站之間的距離決定的。本節依舊使用Ri代表用戶到其第i個服務基站的距離。所以某小區邊緣用戶的發送功率由Rn決定。雖然這樣會造成手機的發送功率過高，但是考慮到用戶處于小區邊緣位置的時間不可能太長，所以可以認為這樣的假設是合理的。

對于上行鏈路信道的建模，同樣使用與下行鏈路相同的由文獻[12]提出的標準功率衰落傳播模型。考慮到上行鏈路是否覆蓋的判斷標準為至少m個基站收到足夠大的有用信號功率，并且同一用戶對n個服務基站的發送功率均相同，所以可以合理地認為只要第m個基站收到足夠大的有用信號功率，那么就可認為對于使用多小區協作技術的某小區邊緣用戶，其上行鏈路被覆蓋。所以對于上行鏈路，文中的分析目標為該用戶的第m個服務基站。

3.2 上行鏈路覆蓋概率

假設整個空間中的手機用戶分布服從強度為λu的泊松點過程Φu。在整個空間中，可以不失一般性地認為特定用戶的第m個服務基站處于空間的原點。對于處于原點的基站，其收到的來自特定用戶的信號功率可以表示為：

(11)

其中，hm表示用戶到其第m個服務基站的信道，且服從均值為1/μ的指數分布。

雖然該用戶不再處于原點位置，但是他與其服務基站的相對位置并未改變。所以Rn，Rm的概率密度函數依舊符合式(6)。

(12)

分析第m個服務基站收到的干擾信號。考慮到文中分析范圍為整個空間，小區邊緣用戶數量只占空間中所有用戶的很小一部分，并且小區邊緣用戶距離所有基站的位置都較遠，所以可忽略小區邊緣用戶的信號對特定基站產生的干擾。本節只用考慮小區內普通用戶對于特定基站的干擾。

基于以上分析可知，對于特定小區邊緣用戶的第m個服務基站來說，其收到的干擾信號功率為整個空間中普通用戶發送信號功率之和。又根據泊松點過程中刪去有限個點不改變泊松點過程分布的性質，可以認為這些空間內普通用戶依舊服從強度為λu的泊松點過程Φu。由于文中假設小區內的普通用戶并不使用多小區協作，而是只與距其最近的基站進行通信。所以處于p點的小區普通用戶到距其最近的基站之間的距離用Bp表示，而p點到原點(目標基站)的距離用Dp表示。所以目標基站收到的干擾功率為：

(13)

根據上行鏈路覆蓋概率的定義得，上行鏈路覆蓋概率表達式為：

此處考慮分子分母上同時存在參數k，可消去。

又根據拉普拉斯變換性質和hm～exp(μ)可知：

(15)

根據文獻[13]可知，上行鏈路干擾信號的拉普拉斯變換為：

(16)

(17)

其中，式(16)是根據hm～exp(μ)得到的；式(17)是根據泊松點過程的概率生成泛函(PGFL)求得的。

式(17)中積分的上下界表明空間中的所有普通用戶均視作某小區邊緣用戶上行鏈路的干擾用戶。而根據文獻[13]可知，對與某用戶最近的基站是隨機分布于某用戶的Voronoi圖中的，所以隨機變量BP的概率密度函數依舊符合式(6)，表達式為：

(18)

最終將式(18)依次帶入式(14)就可得到上行鏈路的覆蓋概率最終表達式。

4 數學分析

本節利用上兩節推導出的結果進行Matlab仿真[15]，并分析結果。以下如無特殊說明均假設路徑損耗因子α=4。

在下行鏈路中，認為某小區的邊緣用戶能夠收到來自一個基站組所發送的信號。為了便于分析，只考察n=2,3,4的簡單情況。該基站組對于某小區邊緣用戶的覆蓋概率隨信干比門限的變化如圖1所示。

圖1 下行鏈路覆蓋概率

由圖1可見，由于小區用戶能夠收到來自多個基站的信號，其下行鏈路覆蓋概率能夠得到明顯的提升，且隨著選擇的協作基站的數目越多，其覆蓋概率的提升越明顯。

在上行鏈路中，文中假設對于小區內的某個邊緣用戶來說，它會選擇不同數量的協作基站，并且同時為了能夠比較，選擇最近的基站作為分析的上行鏈路目標基站(m=2，3)。在實際情況中，由于手機本身功率的限制，上行鏈路中不能選擇過多的服務基站，所以也只考慮n=3,4的情況。得到的上行鏈路覆蓋概率隨著信干比門限T的變化如圖2所示。

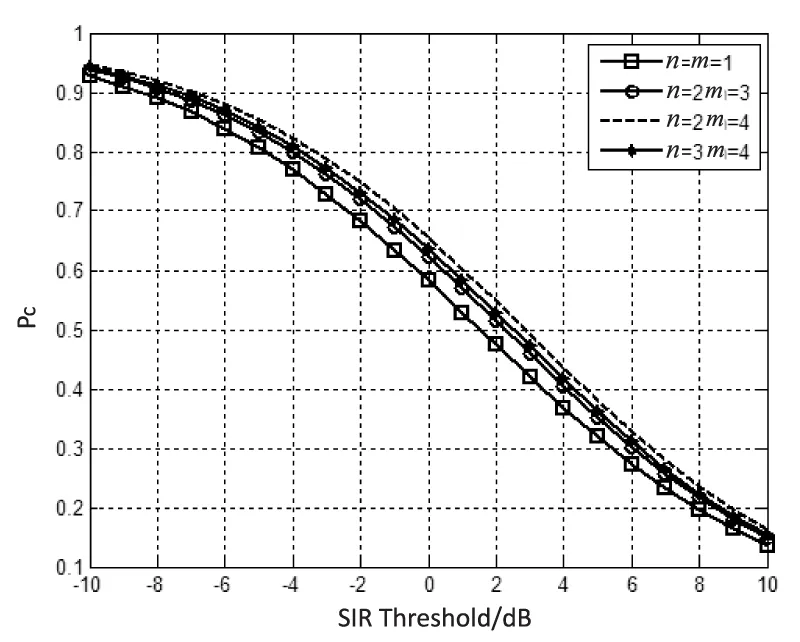
圖2 上行鏈路覆蓋概率

從圖2可以看出，由于在上行鏈路中采用了多小區協作技術，上行鏈路中手機用戶對于目標基站的覆蓋概率隨著選擇的基站數目增加而增加，這是為了盡可能多地覆蓋所選擇的目標基站而增大手機的發送功率所引起的。

5 結束語

文中提出了一種基于隨機幾何理論的框架，對使用多小區協作技術的蜂窩網絡的上行鏈路和下行鏈路分別進行建模，重點討論了利用泊松點過程的數學性質推導對于小區內的隨機選擇的任意用戶，在使用多小區協作技術的情況下，上行和下行鏈路覆蓋概率具體的數學表達式。該式能夠適用于分析任意位置小區邊緣用戶的覆蓋概率。分析了在使用多小區協作的情況下，小區中邊緣用戶的上行和下行鏈路的覆蓋概率。相較于不使用多小區協作，用戶只和距離其最近基站通信的情況，使用多小區協作能夠提升上行和下行鏈路的覆蓋概率，達到了提升小區邊緣用戶通信質量的目的。

[1] 史 聃,朱近康.分布式天線小區協作通信系統下行鏈路頻譜效率的研究[J].中國科學技術大學學報,2009,39(5):479-483.

[2] 駱 純.LTE-AdvancedCoMP中聯合處理技術及系統性能研究[D].武漢:武漢理工大學，2010.

[3]WynerAD.Thewiretapchannel[J].BellLabsTechnicalJournal,1975,54(8):1355-1387.

[4]ShamaiS,ZaidelB.Enhancingthecellulardownlinkcapacityviaco-processingatthetransmittingend[C]//Procof53rdIEEEvehiculartechnologyconference.[s.l.]:IEEE,2001:1745-1749.

[5]SomekhO,ZaidelB,ShamaiS.Sumratecharacterizationofjointmultiplecell-siteprocessing[J].IEEETransactionsonInformationTheory,2007,53(12):4473-4497.

[6]JingS,TseDNC,SoriagaJB,etal.Multicelldownlinkcapacitywithcoordinatedprocessing[J].EURASIPJournalWirelessCommunicationsandNetworking,2008,2008:586878.

[7]WynerAD.Shannon-theoreticapproachtoaGaussiancellularmultiple-accesschannel[J].IEEETransactionsonInformationTheory,1994,40(11):1713-1727.

[8] 呂星哉,王 振,朱近康.三角形蜂窩小區的遍歷信息論容量分析[J].電子與信息學報,2008,30(4):801-804.

[9]ElSawyH,HossainE,HaenggiM.Stochasticgeometryformodeling,analysis,anddesignofmulti-tierandcognitivecellularwirelessnetworks:asurvey[J].IEEECommunicationsSurveys&Tutorials,2013,15(3):996-1019.

[10]HaenggiM,AndrewsJ,BaccelliF,etal.Stochasticgeometryandrandomgraphsfortheanalysisanddesignofwirelessnetworks[J].IEEEJournalonSelectedAreasinCommunications,2009,27(7):1029-1046.

[11]AndrewsJ,BaccelliF,GantiR.Atractableapproachtocoverageandrateincellularnetworks[J].IEEETransactionsonCommunications,2011,59(11):3122-3134.

[12] 李國通,仇佩亮,徐綠洲.FDD-CDMA的下行鏈路的波束形成[J].電子學報,1999,27(12):76-79.

[13]NovlanTD,DhillonHS,AndrewsJG.Analyticalmodelingofuplinkcellularnetworks[J].IEEETransactionsonWirelessCommunications,2013,12(6):2669-2679.

[14] 郭 健,鄭迺錚,談振輝.LTE-A上行CoMP軟信息合并接收算法[J].電信科學,2012(8):53-57.

[15] 余金蓉.多小區協作系統的仿真實現及性能分析[J].計算機技術與發展,2013,23(11):258-260.

Analysis of Multi-cell Coordination Network Based on Stochastic Geometry Approach

CAI Jie,LIU Chen，LU Feng

(School of Electronic Science and Engineering，Nanjing University of Posts and Telecommunications，Nanjing 210046，China)

In response to the problem of poor communication quality suffered by edge residential users in congested cellular network,one of feasible methods is to employ multi-community collaboration technology.But now the Wyner model cannot analyze this technology accurately.In this paper,the Poisson point process is used to model the cellular community,which is able to accurately analyze communication quality of users in the scenario of edge residential users employing multi-community collaboration technology.The accurate mathematical expressions of coverage probability in uplink and downlink regarding any user within the community are calculated using stochastic geometry tools.The result shows the multi-community collaboration technology can heavily promote the coverage ability.With the adequacy of collaboration,it can bring more enhancement in coverage ability.

cellular network;multi-cell coordination;Poisson point process;coverage probability;stochastic geometry

2015-09-15

2015-12-23

時間：2016-05-25

國家自然科學基金資助項目(61372126，61302101)

蔡 杰(1991-)，男，碩士研究生，研究方向為智能信號處理；劉 陳，博士生導師，教授，研究方向為無線通信中的信號處理、空時編碼；陸 峰，副教授，研究方向為隨機幾何理論。

http://www.cnki.net/kcms/detail/61.1450.TP.20160525.1709.046.html

TN929.5

A

1673-629X(2016)06-0200-05

10.3969/j.issn.1673-629X.2016.06.045