能量因子修正的常數(shù)模盲均衡

肖　瑛，丁紀峰

(大連民族大學 信息與通信工程學院，遼寧 大連 116605)

?

能量因子修正的常數(shù)模盲均衡

肖瑛，丁紀峰

(大連民族大學 信息與通信工程學院，遼寧 大連 116605)

摘要：針對通信信號傳輸過程中能量損耗影響常數(shù)模盲均衡收斂性能問題，提出了一種能量因子修正的常數(shù)模盲均衡算法。通過在常數(shù)模代價函數(shù)中引入能量因子，對接收信號功率進行放大，以滿足SW定理在盲均衡實現(xiàn)中對傳輸信號能量的約束條件。能量因子采用梯度下降算法進行自適應調整，解決了能量因子估計困難問題。能量因子修正的常數(shù)模盲均衡算法在能量因子約束條件下對代價函數(shù)進行尋優(yōu)，可有效提高算法的收斂性能，并且改進方法體現(xiàn)在對代價函數(shù)的修正上，可推廣到基于梯度算法的各類改進常數(shù)模盲均衡算法中。仿真結果表明，文中提出的方法與傳統(tǒng)CMA算法相比具有更快的收斂速度和更小的穩(wěn)態(tài)剩余誤差。

關鍵詞：盲均衡；常數(shù)模算法；能量因子；SW定理

盲均衡技術由于不需訓練序列即可實現(xiàn)對通信信道的補償和跟蹤，可有效節(jié)省通信帶寬，提高通信效率和通信質量[1]，特別是在非合作通信中盲均衡技術具有潛在的應用價值。在各類盲均衡算法中，常數(shù)模算法(Constant Modulus Algorithm，簡稱CMA)由于收斂穩(wěn)健、實現(xiàn)簡單而得到了廣泛應用[2]。SW定理[3-4]指出，發(fā)送信號與接收信號功率相等的條件下，接收觀測信號峰度最大化是實現(xiàn)盲均衡的充分條件。在通信信號傳輸過程中，信號的能量損耗不可避免，對接收觀測信號能量進行合理補償可有效提高盲均衡的性能。CMA隱含利用了接收觀測信號的高階統(tǒng)計特征，在CMA的基礎上，進一步考慮接收觀測信號能量補償問題，可使算法滿足SW定理提出的約束條件，改善均衡性能。由于盲均衡技術的實現(xiàn)無需發(fā)送信號和信道特性的先驗信息，因此無法事先對通信信號傳輸過程中的能量損耗進行定量估計。文中在分析CMA代價函數(shù)的基礎上，引入能量因子對接收觀測信號的能量進行修正，并采用梯度下降算法對能量因子進行自適應估計，以解決能量因子定量估計困難問題。能量因子修正的CMA改進算法僅對代價函數(shù)進行了重新設計，因此該算法可推廣應用到基于梯度算法的各類改進CMA盲均衡算法中。最后利用計算機仿真驗證了文中提出方法的有效性。

1能量因子修正的常數(shù)模盲均衡

1.1　CMA盲均衡基本原理

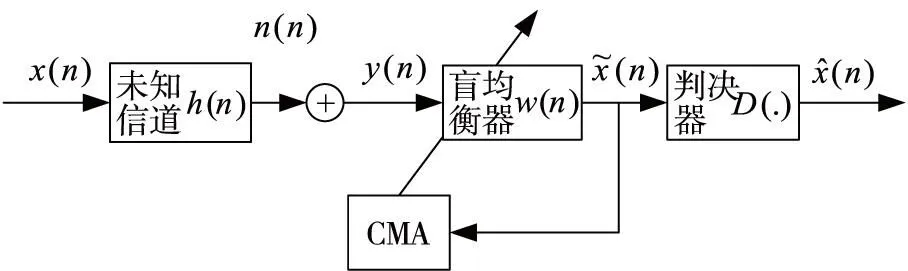
圖1　CMA等效基帶原理框圖

根據(jù)通信信號傳輸原理可知

y(n)=h(n)?x(n)+n(n)，

(1)

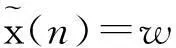
(2)

符號“?”表示卷積運算。CMA根據(jù)常模標準設計代價函數(shù)，通過最小化代價函數(shù)實現(xiàn)盲均衡，CMA代價函數(shù)為[7]

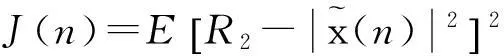
(3)

式中，R2為常模，可根據(jù)接收觀測信號的統(tǒng)計特性進行計算

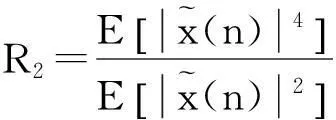
(4)

根據(jù)隨機梯度下降算法原理[8]，最小化代價函數(shù)可根據(jù)式(5)實現(xiàn)

w(n+1)=w(n)-μΔJ(n)，

(5)

式中，μ為學習步長，控制著算法的收斂速度和收斂精度。根據(jù)最小均方誤差原理，利用瞬時梯度代替期望梯度，可以得到

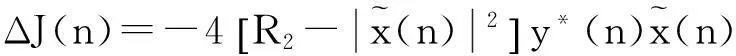
(6)

令誤差函數(shù)e(n)為

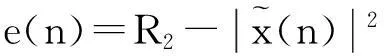
(7)

則均衡器的更新公式[9]可以寫為

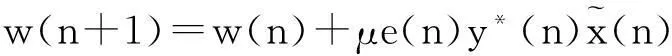
(8)

式(8)中應含有系數(shù)4，考慮該系數(shù)可以融入步長一并計算，因此在均衡器的更新公式(8)中忽略該系數(shù)。

1.2　能量因子修正CMA代價函數(shù)

O.Shalvi和E.Weistein利用信號的二、四階累積量證明了實現(xiàn)盲均衡的一個充要條件，也稱為盲均衡實現(xiàn)的峰度準則[3-4，10]，峰度準則指出如果發(fā)送信號與接收信號的功率相等，即

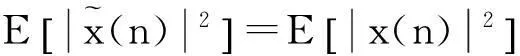
(9)

則有

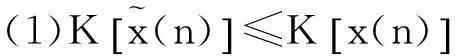
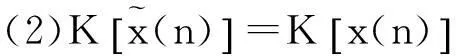
其中K[.]表示峰度，式(1)和式(2)構成的盲均衡實現(xiàn)的充要條件也稱為SW定理，由SW定理可知，發(fā)送信號與接收信號具有相同功率是盲均衡實現(xiàn)理想均衡的約束條件。而實際通信傳輸過程中，傳輸信號的能量損耗不可避免。針對通信信號傳輸過程中的能量損耗，在均衡器前端加入能量因子γ對接收觀測信號功率進行控制，原理框圖如圖2。可以證明的是該能量因子加在均衡器的輸入端和輸出端是等價的，根據(jù)圖2可以知均衡器的輸出為

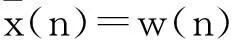
(10)

因此能量因子γ加在均衡器前端和后端具有同樣的效果。這樣CMA代價函數(shù)可以修改為

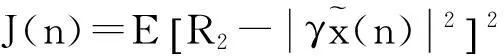
(11)

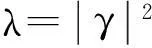
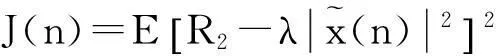
(12)

由于系數(shù)λ>0是未知的，因此將λ看作代價函數(shù)的一個變量進行自適應調節(jié)，那么代價函數(shù)的形式可以進一步寫作

(13)

最小化代價函數(shù)式(12)即可得到能量因子修正的CMA盲均衡。

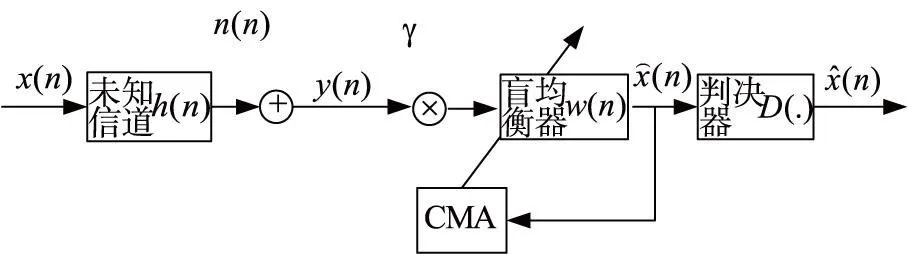
圖2　能量因子修正的CMA原理框圖

1.3　能量因子修正CMA代價函數(shù)

將代價函數(shù)式(13)視為均衡器權系數(shù)與λ(n)的函數(shù)，那么采用梯度下降算法最小化代價函數(shù)等價于

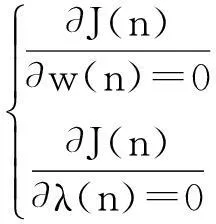
(14)

令誤差函數(shù)

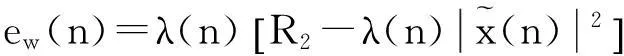
(15)

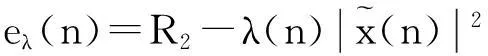
(16)

則均衡器權系數(shù)w(n)與λ(n)的更新公式為

(17)

(18)

式中，μw和μλ分別表示均衡器權系數(shù)w(n)與λ(n)更新的學習步長。利用式(17)和式(18)可最小化能量因子修正的CMA代價函數(shù)，實現(xiàn)盲均衡。

2仿真分析

為驗證能量因子修正常數(shù)模盲均衡算法的性能，在無噪聲和不同信噪比高斯白噪聲條件下進行仿真分析。仿真信道模型采用典型的電話信道[11]，等效基帶沖激響應為

h=[0.04,-0.05,0.07,-0.21,-0.5,0.72,0.36,0,0.21,0.03,0.07]。

(19)

發(fā)送信號為等概率二進制序列，采用QPSK調制方式。線性橫向均衡器長度為45，中心抽頭系數(shù)初始化為1，其余權系數(shù)初始化為0。無噪聲干擾條件下設置μw=0.002，μλ=0.004。利用剩余碼間干擾對算法性能進行評價，剩余碼間干擾[12]用式(20)進行計算。

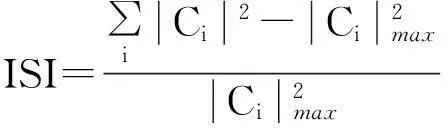
(20)

式中，C表示均衡器與信道的聯(lián)合沖激響應向量。500次蒙特卡洛仿真得到的剩余碼間干擾收斂曲線如圖3，能量因子λ(n)的變化曲線如圖4。

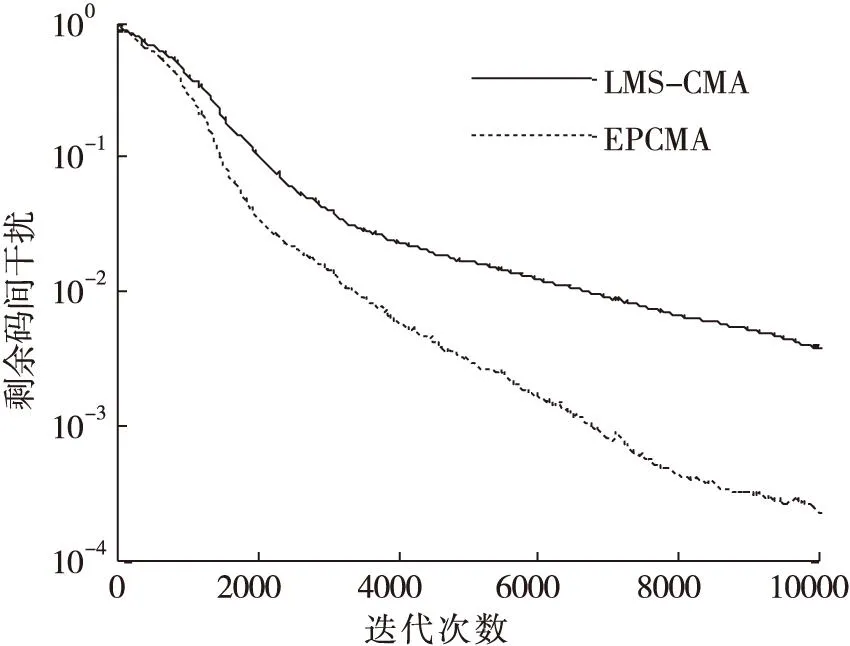
圖3　無噪條件下的ISI收斂曲線

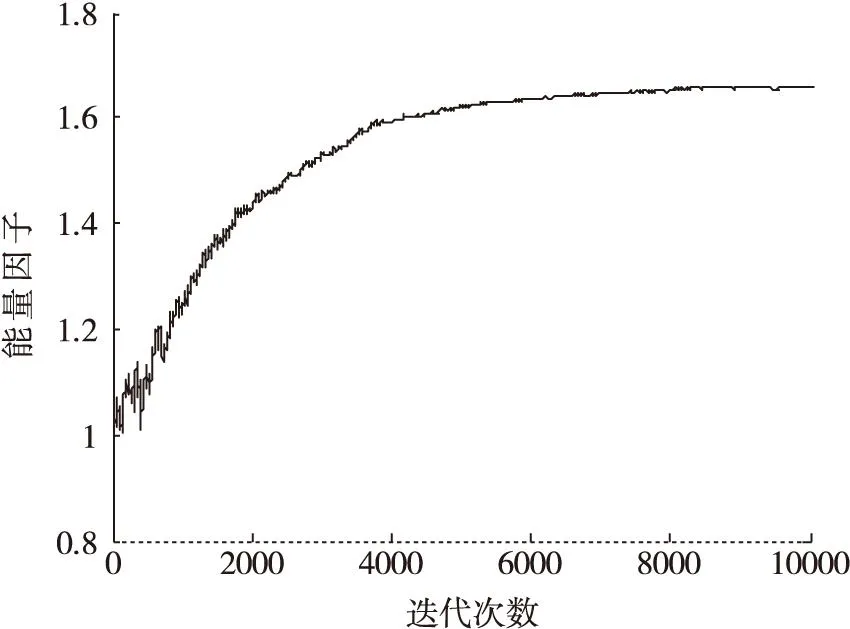
圖4　無噪條件下能量因子變化曲線

由圖3可知，文中提出的能量因子修正的常數(shù)模盲均衡(EPCMA)與CMA相比具有更快的收斂速度，在仿真無噪條件下，收斂速度約快3000步，收斂后具有更小的穩(wěn)態(tài)剩余誤差。從圖4中可以看出，能量因子λ(n)逐漸收斂至一個常值，該值為最小化EPCMA代價函數(shù)的最優(yōu)解。由于能量因子λ(n)無法事前確定，因此EPCMA采用自適應更新能量因子的方法解決了λ(n)估計的難題。

為了進一步驗證EPCMA算法的性能，在上面仿真條件下，改變信噪比各進行500次蒙特卡洛仿真，觀察算法剩余碼間干擾的收斂性能和能量因子的變化規(guī)律。仿真結果圖5a-圖11b所示。

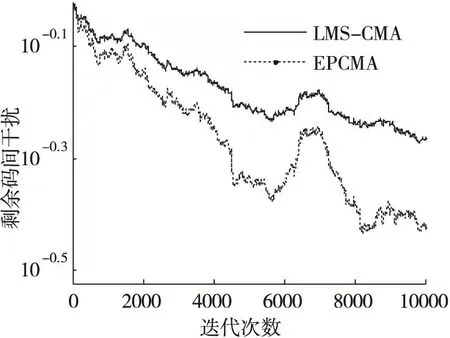
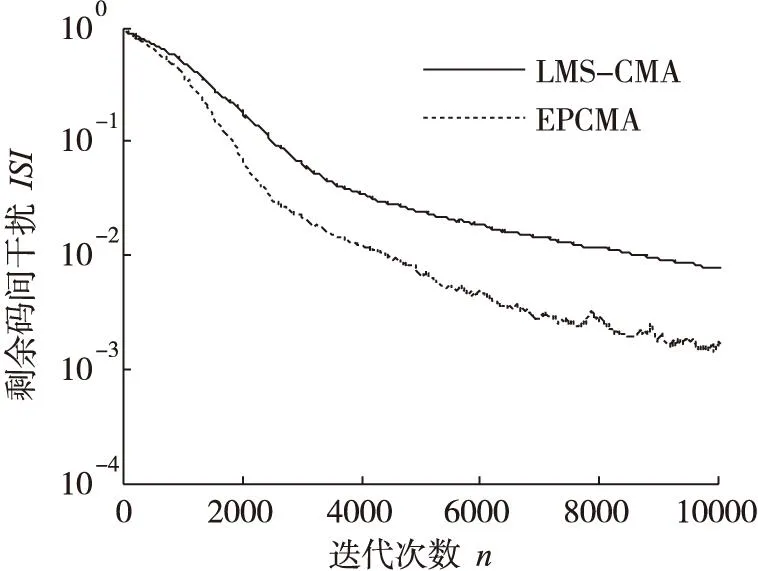
(a)ISI收斂曲線

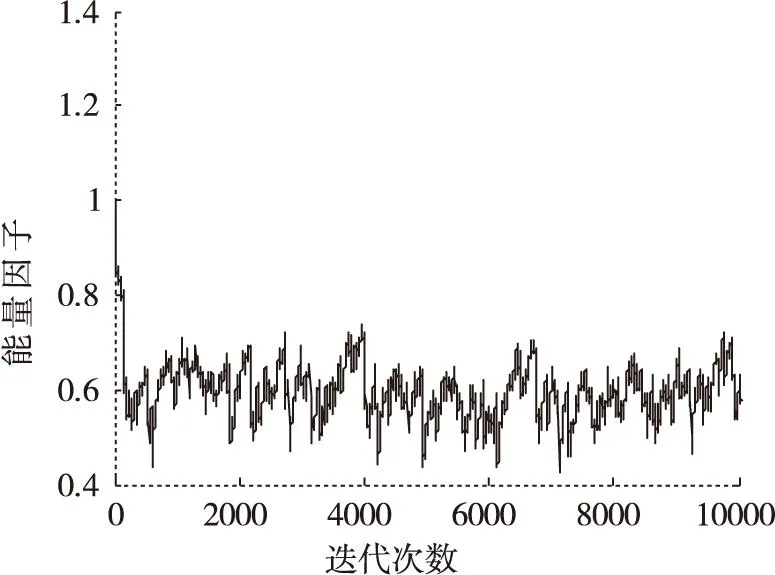
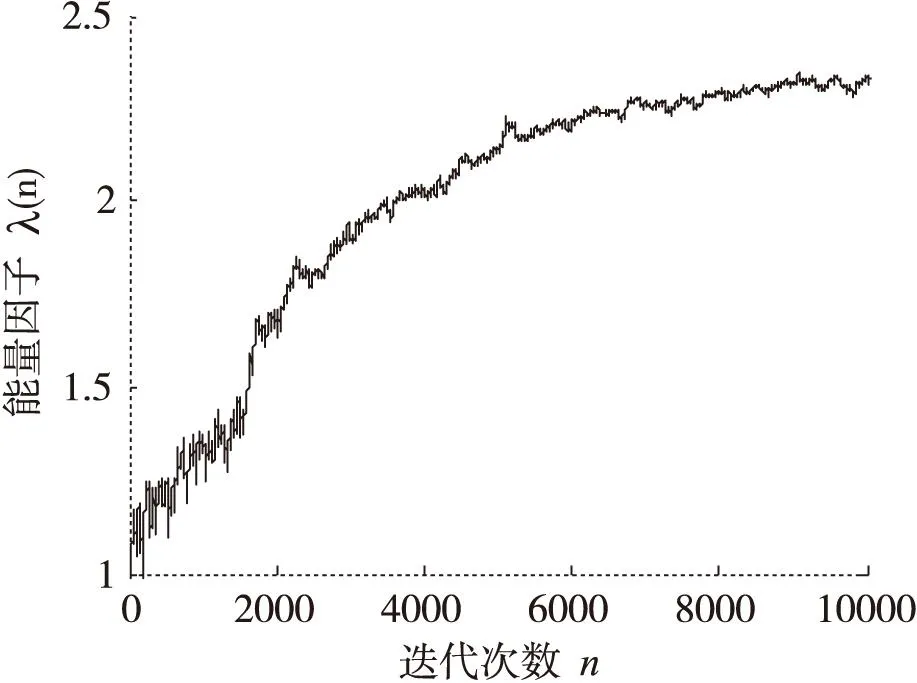
(b)能量因子變化曲線

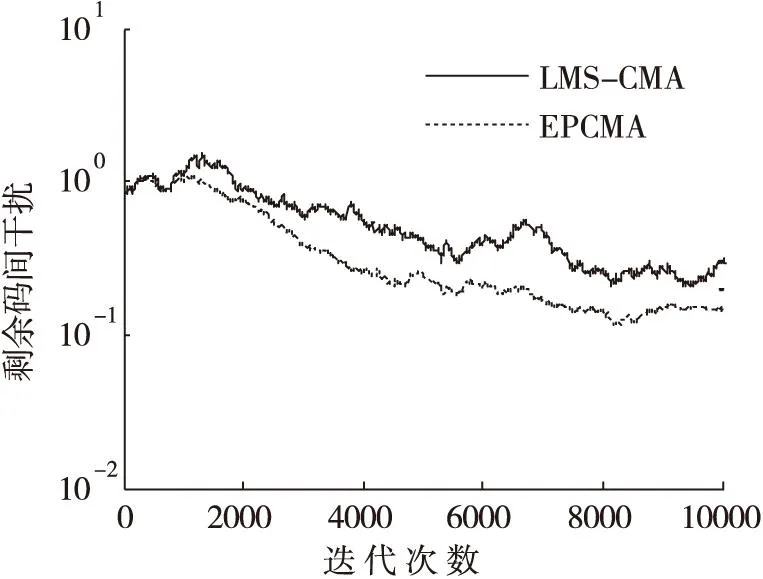
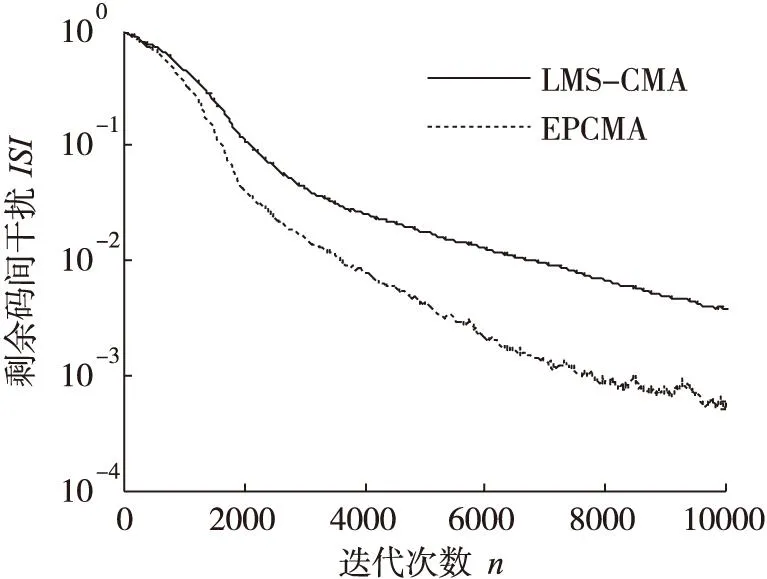
(a)ISI收斂曲線

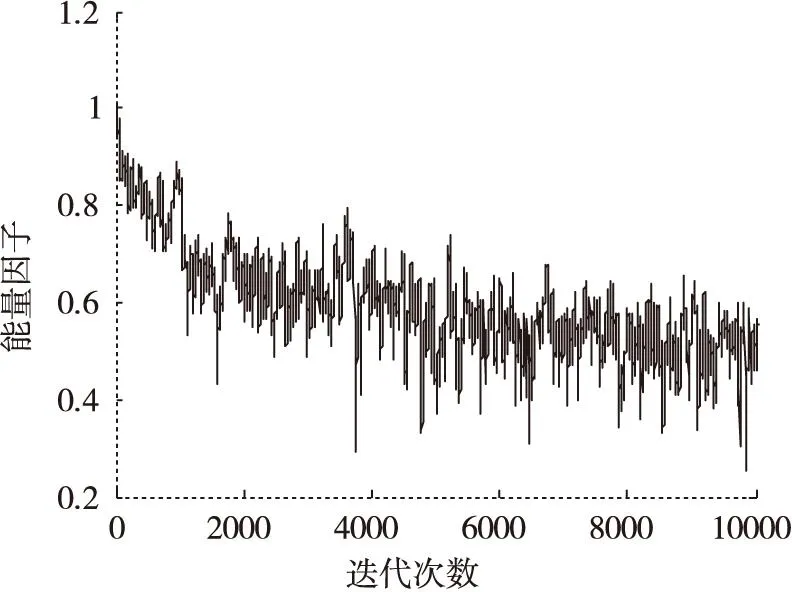
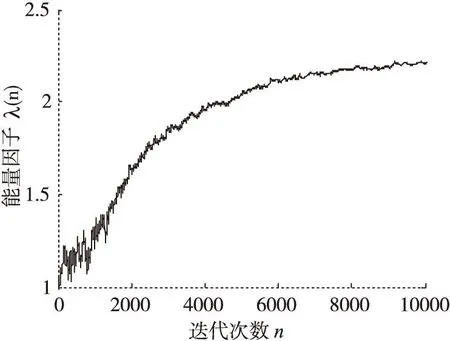
(b)能量因子變化曲線

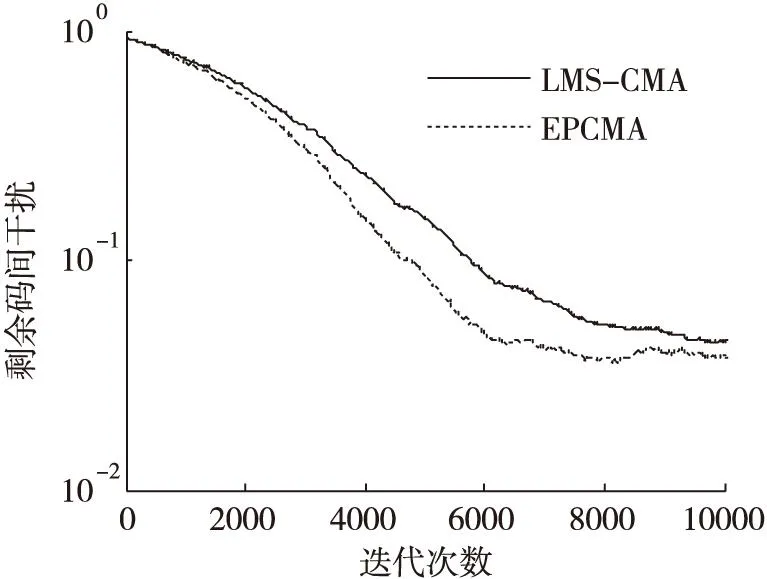
(a)ISI收斂曲線

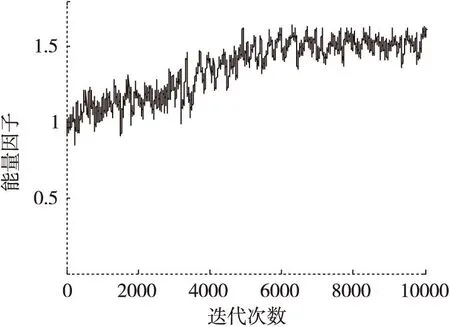
(b)能量因子變化曲線

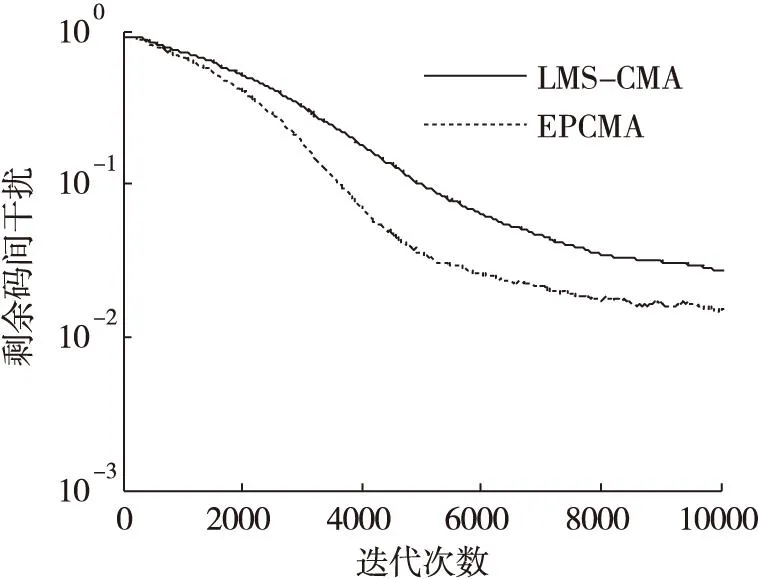
(a)ISI收斂曲線

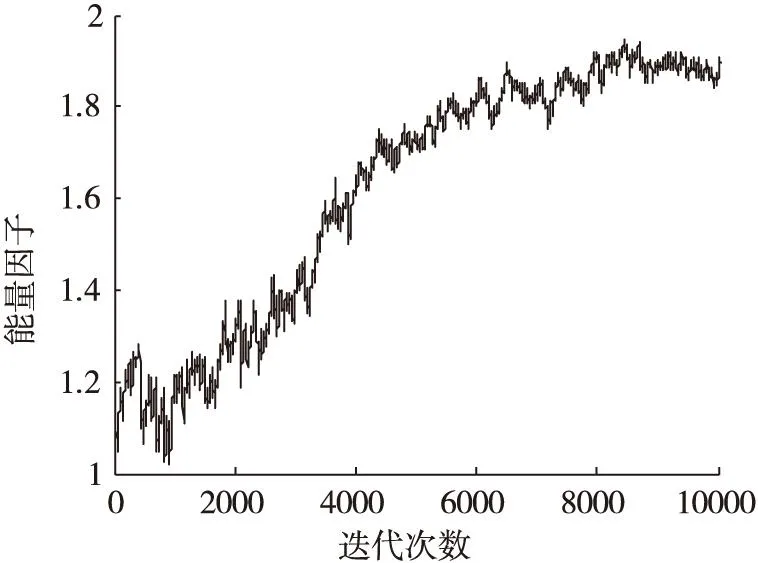
(b)能量因子變化曲線

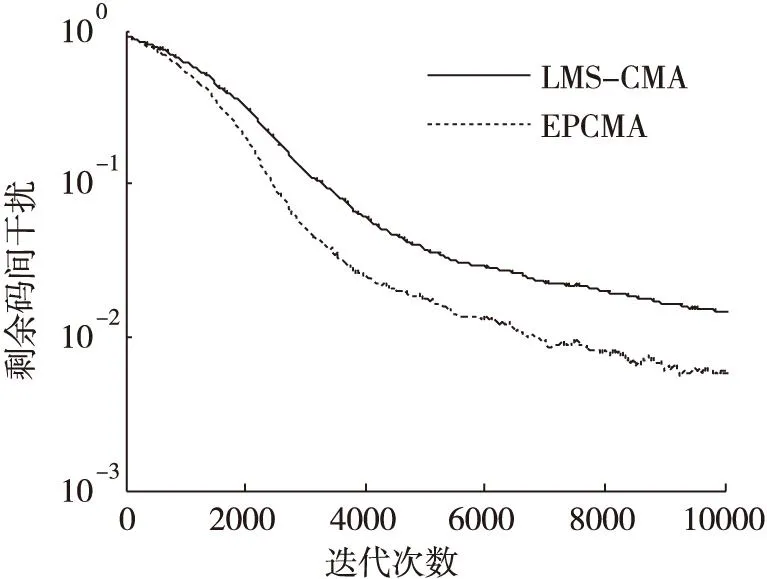
(a)ISI收斂曲線

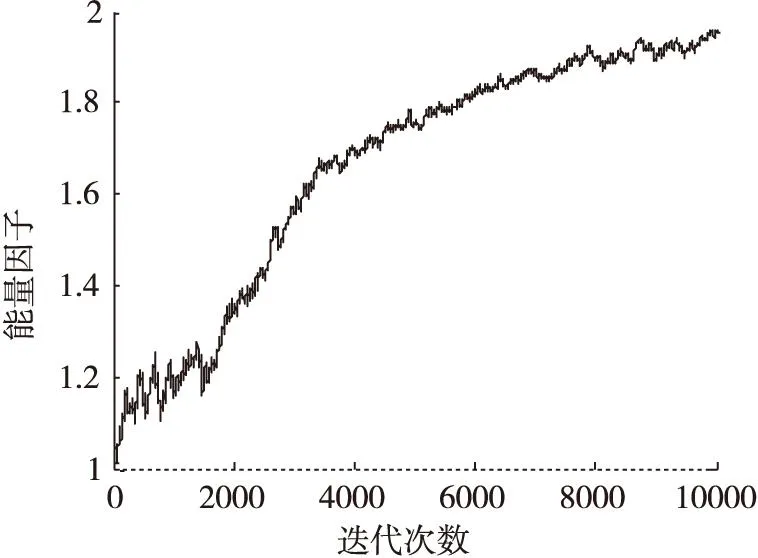
(b)能量因子變化曲線

(a)ISI收斂曲線

(b)能量因子變化曲線

(a)ISI收斂曲線

(b)能量因子變化曲線

通過在不同信噪比條件下的仿真結果可以看出，在低信噪比條件下(SNR<10dB)，能量因子λ(n)在迭代過程中逐漸趨于一個小于1的穩(wěn)定值，這是因為在較低信噪比條件下，能量因子大于1在放大信號能量的同時會導致噪聲放大，反而會降低算法收斂性能。當信噪比SNR≥10dB時，能量因子λ(n)在算法迭代過程中逐漸增大，并趨向于一個大于1穩(wěn)定值，這說明當信噪比SNR≥10dB時，對接收觀測信號能量進行放大會改善常模盲均衡的收斂性能。由圖5a-圖11b中的剩余碼間干擾收斂曲線中可以看出，EPCMA均獲得了比傳統(tǒng)CMA算法更快的收斂速度和更小的穩(wěn)態(tài)剩余誤差，證明了EPCMA是一種有效的常模改進算法。

3結語

文中在對CMA盲均衡分析的基礎上，提出了一種能量因子改進的CMA代價函數(shù)，采用自適應更新策略解決能量因子估計困難問題。利用計算機仿真對算法性能進行了驗證，并得到了在不同信噪比條件下能量因子的收斂規(guī)律，仿真結果證明了算法的有效性。能量因子改進的CMA代價函數(shù)可以推廣到其他基于梯度算法的CMA改進算法中，因此EPCMA盲均衡在實際應用中具有一定的推廣價值。

參考文獻：

[1] HWANG K, CHOI S. Blind equalizer for constant-modulus signals based on Gaussian process regression [J]. Signal Processing, 2012, 92(6): 1397-1403.

[2] OZEN A, KAYA I, SOYSAL B. A supervised constant modulus algorithm for blind equalization[J]. Wireless Personal Communications, 2012,62(1): 151-166.

[3] 張賢達，保錚. 通信信號處理[M]. 北京: 國防工業(yè)出版社, 2000.

[4] SHALVI O, WEINSTEIN E. New criteria for blind deconvolution of non-minimum phase systems (channels) [J]. IEEE Trans on information theory, 1990, 36(2): 312-321.

[5] XIAO Ying, YIN Fuliang. Blind equalization based on direction gradient algorithm under impulse noise environment [J]. Wseas Transaction on Communication, 2014, (13):171-177.

[6] 李金明, 趙俊渭, 郭業(yè)才, 等. 一種拖尾噪聲環(huán)境下的穩(wěn)健常數(shù)模盲均衡新算法[J]. 應用聲學, 2010, 29(1): 17-22.

[7] XIAO Ying,YIN Fuliang. Blind Equalization Based on RLS Algorithm Using Adaptive Forgetting Factor for Underwater Acoustic Channel [J]. China Ocean Enginerring, 2014, 28(3): 401-408.

[8] 郭瑩, 邱天爽, 唐洪，等. 脈沖噪聲環(huán)境下的恒模盲均衡算法[J]. 通信學報, 2009, 30(4): 35-40.

[9] LI S, SONG L M, QIU T S. Steady-state and tracking analysis of fractional lower-order constant modulus algorithm [J]. Circuits, Systems, and Signal Processing, 2011,30(6): 1275-1288.

[10] 王大磊, 楊賓, 吳瑛, 等. 一種基于峰度的QAM信號盲均衡與載波相位恢復準則[J]. 電子學報, 2014, 42(7): 1403-1409.

[11] JEPQ T Y, KUN D T. Analysis of the Multimodulus Blind Equalization Algorithm in QAM Communication Systems[J]. IEEE Trans on communications,2005, 53(9):1427-1431.

[12] 夏楠, 邱天爽, 李景春. 穩(wěn)定分布噪聲下基于粒子濾波的多徑時變信道盲均衡算法[J]. 通信學報, 2013, 34(11): 92-99.

(責任編輯王楠楠)

CMA Blind Equalization Modified By Energy Factor

XIAO Ying, DING Ji-feng

(College of Information and Communication Engineering, Dalian Minzu University,

Dalian Liaoning 116605, China)

Abstract:To solve the problem that the energy loss during the transmission in the communication system degrades the convergence performance of CMA blind equalization, a new CMA blind equalization modified by energy factor is proposed. The energy factor is added to the cost function of CMA, which can amplify the power of the received signal to meet the constraints of transmission signal energy to achieve blind equalization in SW theorem. The energy factor uses the gradient descent algorithm for adaptive updating, which can solve the difficult problem of energy factor estimation. The proposed method implements optimizing the cost function under the constraint conditions of the energy factor, which can effectively improve the convergence performance. Furthermore, CMA blind equalization modified by energy factor is designed in the revision of the cost function, which can be extended to all other improved types of CMA blind equalization based on gradient descent algorithm. The simulation results show that the proposed method can obtain faster convergence rate and lower steady state residual error compared with the traditional CMA blind equalization.

Key words:blind equalization; CMA; energy factor; SW theorem

中圖分類號：TN911.5

文獻標志碼：A

文章編號：2096-1383(2016)01-0072-06

作者簡介：肖瑛(1979-)，女，蒙古族，河北隆化人，副教授，博士，主要從事通信信號處理研究。

基金項目：國家自然科學 (61201418);遼寧省高等學校優(yōu)秀人才支持計劃項目(LJQ2013126);中央高校基本科研業(yè)務費專項資金資助項目(DC12010218)。

收稿日期：2015-09-04；最后修回日期：2015-10-15