數學:解題思路藏在實戰經驗中
王雙興 一路

許多同學總是會這樣抱怨:一碰到數學題,我就找不到解題思路,根本不知道題目的突破口在哪里。那么,解題思路從何而來呢?
數學考試,無非就是考查考生對基礎知識和解題技巧的掌握程度。在做題時,我們可以通過審題和回憶所學知識,找到一道題目所考查的一個或幾個知識點,以點連成面,有針對性地完成最終的解答。
首先,從題干切入,明確試題提供給我們什么樣的有效條件。
其次,著眼設問,明確題目的要求是什么。
最后,開始解答,調用相應的基礎知識、解題技巧。
【例題直通車】
以立體幾何為例,比如要證明線面垂直,這個時候就可以采用“逆向思維”,先假定它們是垂直的。那么,證明線面垂直需要哪些條件呢?回歸課本可知,線垂直于面,必然垂直于面上的兩條相交直線。
例如,如果要證明正方體ABCD-A1B1C1D1的底面對角線BD垂直于面AA1C1C,那么題目的切入點便為尋找面AA1C1C上和BD垂直的兩條相交直線。通過“正方體”這一“顯性”條件,可知:
在正方體ABCD-A1B1C1D1中,AC⊥BD
又∵AA1⊥平面ABCD
BD∈平面ABCD
∴AA1⊥BD
又∵AA1∩AC=A
且AA1、AC∈平面AA1C1C
∴BD⊥平面AA1C1C
一般情況下,題目會給出一定的“顯性”條件(對應上文:圖形是正方體),而其他的“隱性”條件(對應上文:AC⊥BD,AA1⊥平面ABCD),就需要你運用學過的知識,根據其他條件或者畫出輔助線來求證。
到了這一步,許多同學一定又開始嘀咕了:臣實在做不到啊!如果你真的做不到,那證明你對基礎知識還不熟悉,實戰經驗不夠。
所以,復習時,我們要把所有與線、面有關的知識,以及所有相關試題的參考答案(證明線面垂直的具體步驟)整理出來,反復鉆研,弄清楚該如何運用抽象條件去解題。這樣做的好處就是可以讓你更加熟悉課本的基礎知識以及解題的套路。當然,這種做法還可以延伸到其他題目。
如何掌握基礎知識和解題技巧?
首先,將課本的定理、概念、公式背熟,研究課本的例題,掌握最基本的技能——能夠運用定理、概念、公式解答最簡單的題目。
其次,總結歷年高考真題、高三數學試卷的高頻考點,將考查同一類知識點(定理、概念、公式)的題目進行歸類,整理出知識點的考查情況。例如,明確解題需要的條件,弄清楚如何利用“顯性”條件,如何根據“顯性”條件推導出“隱性”條件,熟悉完整的推理過程。
【溫馨提示】在訓練的過程中,一定要懂得站上巨人的肩膀,向老師和有能力的同學請教,這樣可以事半功倍。
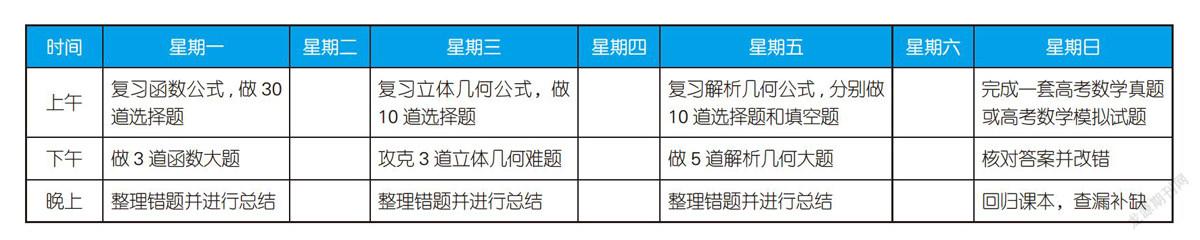
最后,附上一張我個人的數學學習時間表供大家借鑒。

