方形礫巖大小對地層電阻率的影響研究
曹婷
摘要:文章根據礫巖地層的物理特性,建立了方形礫巖地層,推導了地層電阻率的計算公式,并在COMSOL軟件中建立合理的地層模型,數值模擬了礫巖大小對地層電阻率的影響,并與理論結果進行了比較,驗證了數值模擬的合理性。
關鍵字:礫巖大小;孔隙度;地層電阻率;數值模擬
巖石是一種自然生成的混合物,其內含有一定的孔隙,在油氣儲集層內,空隙中一般填充著地層水、石油及天然氣等混合物。根據Archie公式得知,孔隙度是地層電阻率的重要因素之一,而礫巖形狀、大小及排列方式對孔隙的特征有著決定性的作用。本文主要以方形礫巖為例研究了方形礫巖的大小對地層電阻率的影響,為進一步建立接近實際地層的物理模型,研究孔隙度對地層電阻率的影響奠定了基礎。
1 方形礫巖模型及其解析解
圖1(a)所示,為一個棱長為L米的立方體地層模型,(b)為其橫截面及剖面圖,此模型中X,Y,Z方向礫巖排列方向一致,且每個方向上均有5個礫巖,在上表面加等面積大小為I的電流,下表面加等大回路電極。
假設含有礫巖的巖層高度與礫巖長度一樣為h1、不含礫巖的空隙高度為h2,5h1+4h2=L。假設模型是各向同性的,當電流導通后,地層可看作由含礫巖層與不含礫的孔隙層組成的一組串聯電阻,每個含礫巖層可看作是由礫巖和孔隙組成的并聯電路,由電路基礎可知:
根據上述式子有:
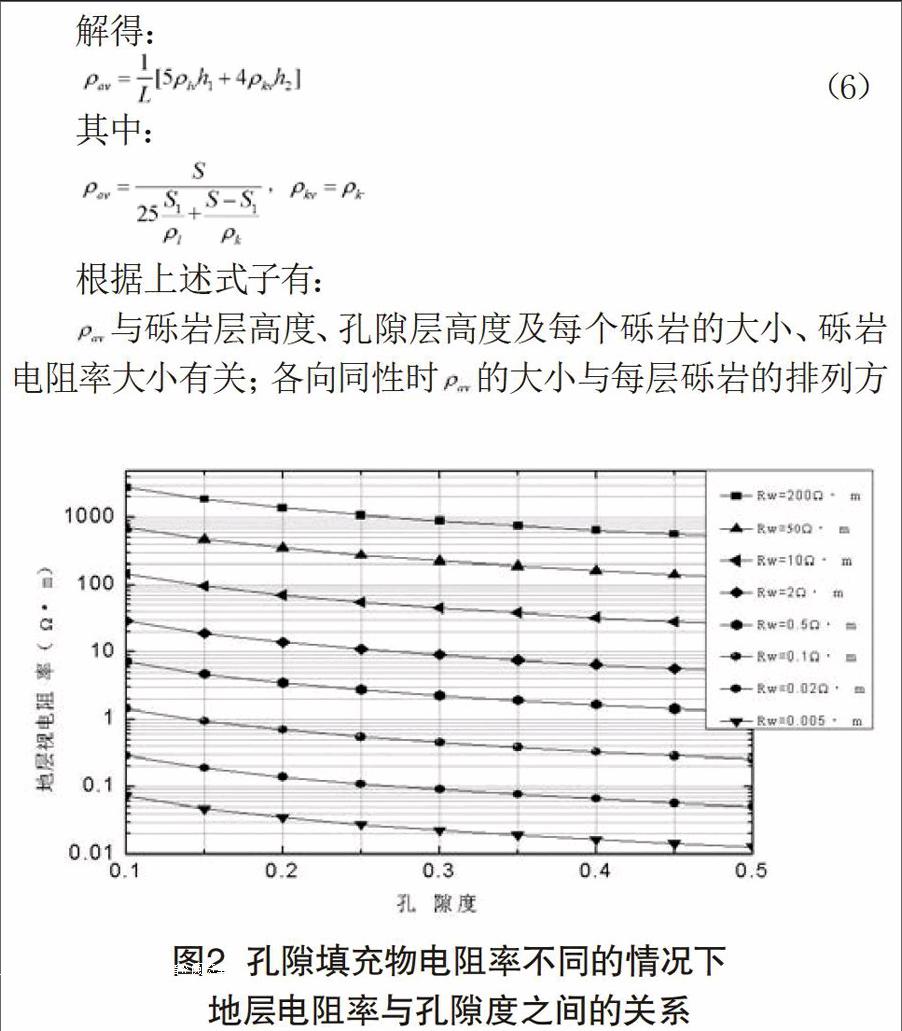
與礫巖層高度、孔隙層高度及每個礫巖的大小、礫巖電阻率大小有關;各向同性時的大小與每層礫巖的排列方式無關。
2 數值模擬礫巖地層電阻率
為驗證如圖1中所示地層模型電阻率公式正確性,本文采用COMSOL多物理場有限元數值計算軟件建立相應地層模型進行數值模擬。結果如圖2所示。圖中為礫巖電阻率為le4Ω·m,孔隙填充物電阻率在0.01~200Ω·m取值時,地層電阻率與地層中孔隙度的關系。
由圖2可知,礫巖越小,孔隙度越大,礫巖對地層電阻率的影響越小,進而說明了礫巖大小對地層電阻率的影響。從數值計算的角度驗證了公式,并與理論結果進行比較,結果一致,說明了數值模擬的合理性。