應力波在二維層狀介質中的傳播特性研究

馬驥　馮軍發

摘 要：應用ABAQUS/Explicit軟件進行動力學顯示分析，選取頁巖、大理巖、花崗巖和玄武巖巖性材料構建二維層狀線彈性模型。以在模型上端面施加一矩形脈沖載荷為例，分析了應力波在分層介質中的傳播特性，并依照模型尺寸，就同一巖性材料分別套用模型，對比分析了應力波在不同介質中的傳播特性受材料固有性質的影響程度。結果表明：①在多層介質模型中，入射應力波的傳播是逐步向四周擴散的，同時，在分界面前后出現反射和透射現象。在“頁巖+玄武巖”分界面，反射擾動起到了加載作用；在“玄武巖+花崗巖”分界面，反射擾動以卸載波的形式阻礙入射擾動傳播；在“花崗巖+大理巖”分界面，由于這兩種巖性材料的物理屬性相似，可認為其阻抗匹配，入射擾動以無反射的形式通過分界面。②在單一介質模型中，波阻抗與應力峰值呈正相關。③對比分析在層狀模型和單一介質模型中，應力波在不同時刻隨傳播距離的變化趨勢后發現，在1.31 μs時，入射應力集中，層狀模型應力峰值最大且變化范圍大，應力波傳播距離比任一單一介質模型都要小；在2.67 μs和5.64 μs時，入射應力擴散，層狀模型應力峰值小于單一介質模型，但其傳播距離大于頁巖性單一介質模型。

關鍵詞：應力波；二維層狀介質；波阻抗；傳播特性

中圖分類號：O347.3 文獻標識碼：A DOI：10.15913/j.cnki.kjycx.2016.04.007

隨著開采深度的不斷加大和地下空間的開發利用，采礦工程逐步向深部發展，巖爆、沖擊礦壓等動力災害事故頻發。事故發生的動載擾動主要以震動波、爆炸波和沖擊波等形式在地下巖體中迅速傳播。地下巖體大多是由多種不同屬性、不同厚度、不同組分按某種方式組合而成的天然層狀體。掌握動載擾動在層狀巖體中的衰減、能量耗散及其傳播特性對指導礦山安全開采和避免緊急事故發生具有十分重要的意義。

近年來，國內外專家學者對應力波在巖石和巖體結構面處的傳播特性做了大量的研究工作：王觀石、李長洪等人研究了應力波在存在非線性結構面塊體中的傳播特性；張奇通過理論公式的推導研究了當垂直于節理入射時，應力波在節理內充填物中的傳遞過程；陳虬、任輝啟運用多重尺度的漸近混合理論，建立了各向同性層狀介質中彈性諧波傳播的特征方程，然后通過數值計算進行了彌散效應分析；劉婷婷、李建春等人研究了應力波通過非線性平行節理時的能量傳遞規律，具體分析了節理的力學特性、空間分布以及應力波物理特性的變化影響能量的傳遞變化規律；叢文相、孫豪志提出了一種識別二維層狀介質中地震波速度的新方法，并證明了這一方法的可行性；董永香、馮順山等人應用非線性軟件LS-DYNA對一維應變下不同組合多層介質中爆炸波的傳播進行了數值模擬，分析了不同組合方式的多層介質和軟夾層材料對爆炸波波形、幅值和能量的影響；趙堅、陳壽根等人應用離散元程序UDEC和有限差分程序AUTODYN-2D，模擬了節理巖體中爆炸波的傳播和不同節理與波的相互作用，證明了應用數值模擬軟件研究應力波傳播問題的可行性；劉彪、陸菜平、竇林名等人利用FLAC3D數值模擬軟件的Dynamic模塊，將井下實測的一次沖擊礦壓信號作為震源，模擬研究了沖擊震動波在不同煤巖介質中的傳播特性，并通過現場工程實踐驗證了震動波在弱巖層結構中傳播的衰減效應；C.HAN和C.T.SUN通過構建具有周期性交替的不同材料的線彈性介質層的理論模型，研究了波前衰減和應力波空間衰減規律，同時，分析了層厚比、層狀介質固有的屬性和本身厚度對應力波傳播的影響。

本文主要應用Abaqus有限元分析軟件進行數值模擬：構建二維線彈性層狀巖性體模型，分析接觸層面前后應力變化情況；通過與單一介質模型進行對比，分析應力波的傳播特性；分析巖性體波阻抗對應力峰值的影響。

1 應力波在介質層面傳播的理論模型

當任一彈性波到達介質分界面時（假設分界面沒有相對滑動，且都為彈性介質巖體），會產生四種波的作用，即反射無旋波、反射等容波、折射無旋波和折射等容波。根據分界面上的連續性條件和Snell定律可以得出彈性縱波斜入射在分界面上的反射和折射情況如圖1所示。

根據式（14）和式（15），即可求得反射和透射彈性應力波的波速。

2 數值模擬模型

層狀巖體是煤巖的一種附在狀態。應力波傳播通過層狀介質面時勢必會發生反射和透射現象，并時刻伴隨著能量耗散。數值模擬采用有限元分析軟件Abaqus中的Explicit模塊。該模塊主要用于顯示動態分析，一般用于求解高速動力學問題、復雜的接觸問題和高速非線性的準靜態問題，特別適用于求解模擬沖擊、爆炸等的動態問題。為簡單起見，本文選取由不同厚度的頁巖、玄武巖、花崗巖、大理巖板拼合構成二維層狀模型，材料力學參數見表1，尺寸（長×高）為0.65 m×0.425 m。該模型采用線彈性模型（即動態擾動引起的應力波僅以彈性波的形式存在），單元類型為CPS4R（四結點雙線性平面應力四邊形單元，減縮積分），劃分網格的結點總數為14 605，單元總數為14 153，具體模型如圖2所示。

在模型坐標為（0.415，0.425）處沿y軸軸向施加一矩形脈沖載荷，其載荷加載模型如圖3所示。該矩形脈沖載荷函數表達式為：

脈沖載荷的寬度為t1=0.5 μs，所加脈沖載荷峰值為0.2E6 N，其時程曲線如圖4所示。主要模擬應力縱波沿路徑通過層狀分界面時應力波的傳播特性。

僅將二維層狀模型改變為同種巖性的實體模型，如圖5所示，模擬應力波在單一介質模型中的傳播特性，目的是與層狀巖體應力波傳播特性進行對比；同時，比較分析不同單一介質應力波峰值與介質本身波阻抗的關系。

4 數值模擬結果與分析

4.1 二維層狀介質模型應力波傳播特性

在作用載荷點周圍會瞬時產生球面波。隨著球面波的擴散，在離該中心點較遠處，可將其簡化為彈性平面波的傳播。以動載擾動源為原點構建直角坐標系，沿y軸正方向分別選取分界面附近測試單元，其具體布置如圖6所示。

由不同介質本身性質間的差異可以求出頁巖、玄武巖、花崗巖和大理巖中應力波的傳播速度分別為：

由已知的各個二維模型的高度，可計算出應力波在頁巖、玄武巖、花崗巖和大理巖介質中傳播的時間分別為1.31 μs、1.36 μs、2.97 μs 和2.95 μs。圖7中，（a）（b）（c）分別為分界面1、分界面2和分界面3處各測試單元的應力波時程曲線。

4.2 同尺寸單一介質模型應力波傳播特性

研究了層狀模型中應力波在分界面處的反射和透射現象后，下面將分析在單一介質模型、同樣的動載荷擾動情況下應力波的變化情況。分別就大理巖、花崗巖、頁巖、玄武巖建立模型?？紤]到各類巖石物理性質的差異性，模型網格劃分各有不同，其他的設置沒有變化。沿著路徑選取前結點單元、中結點單元和后結點單元，單元布置如圖8所示，繪制出的應力時程曲線如圖9所示。

從圖9（a）可以看出，監測單元1處應力變化比較明顯，約在t=2 μs后，不同的巖體應力波形表現出相同的變化規律，隨著時間的推移，應力波形呈現衰減趨勢。從圖9（b）可以看出，波形完整，且變化明顯，玄武巖在t=4.8 μs后，其應力隨時間衰減明顯，大理巖和花崗巖比較接近，其應力衰減出現在t=6.0 μs后。此時的頁巖在t=5.4 μs時才剛好出現其應力峰值σ=7.5 MPa，說明不同的巖性模型，其應力波衰減規律不同。對比三個單元測點的時程曲線發現同一規律——玄武巖巖體中應力峰值最大且出現得最快，花崗巖和大理巖應力峰值比較接近，頁巖應力峰值在最后出現。從圖9（c）中可看出，當t=8.5 μs時，玄武巖應力波已經到達末端面并發生了反射現象，形成的反射波繼續在巖性體中傳播；而其他各巖性模型在t=8.1 μs時才出現最大應力峰值，證明應力波的波前還未到達模型末端面處。

考慮到波阻抗對應力波傳播的影響，選取不同巖性模型的峰值應力最大值，繪制波阻抗—應力曲線，如圖10所示。

波阻抗（×106 kg/m2·s）

圖10 波阻抗與峰值應力的關系曲線

不同的波阻抗，所反映出的應力峰值變化規律是不同的。由于花崗巖和大理巖的阻抗匹配，因此，其峰值應力接近，這與理論是吻合的。同時，堅硬的玄武巖波阻抗最大，其應力峰值也最大。于是，我們可以得出，波阻抗與應力峰值呈正相關。

5 層狀模型與單一介質模型應力波傳播特性

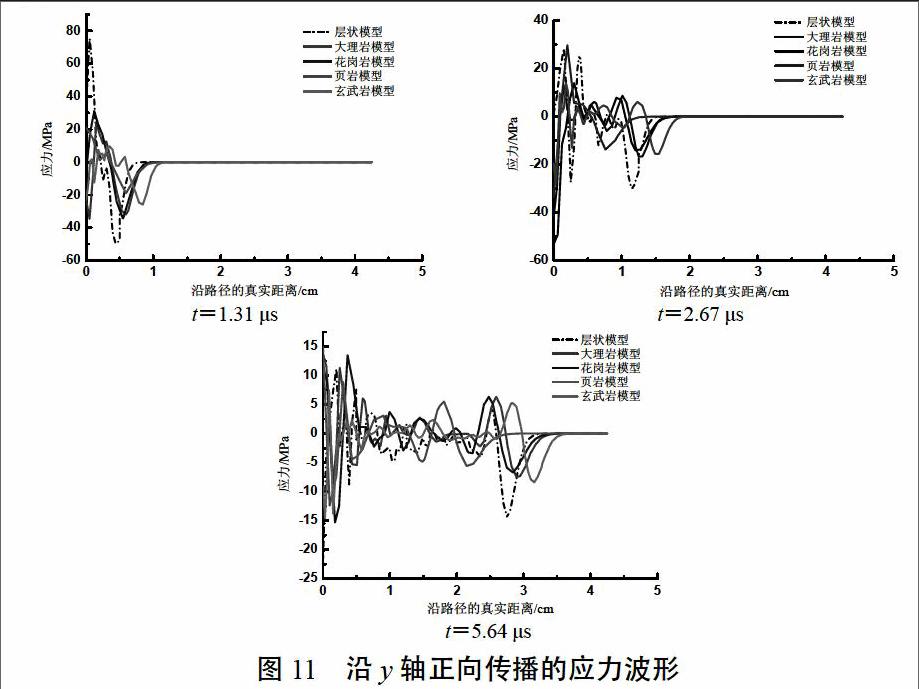
在層狀模型中，載荷源點沿y軸正向到達底端路徑上，取剛好到達分界面時刻（1.31 μs、2.67 μs和5.64 μs）的位移和應力，繪制應力波形圖。同樣，繪制出單一介質模型不同時刻應力沿路徑變化的波形圖。圖11所示為層狀模型與單一介質模型應力波形的變化。從圖中我們可以得出以下一些規律：①在1.31 μs時，在分界面1處，層狀模型的應力波從“軟巖層”進入“硬巖層”，相比于單一介質模型，其應力峰值高且變化范圍較大；對比不同巖性的單一介質模型，楊氏模量最大的玄武巖模型應力波的傳播距離最遠，花崗巖與大理巖模型相近，應力波的傳播距離十分接近，頁巖模型應力波的傳播距離最??；由于有“軟巖層”的存在，層狀模型應力波波速較慢，其傳播距離要比任一單一介質模型都要小。②在2.67 μs時，在分界面2處，應力波由“硬巖層”進入“軟巖層”，反射應力波的卸載作用導致其應力峰值變小。由此可看出，層狀模型應力波的傳播距離要大于頁巖模型中應力波的傳播距離。這是因為頁巖模型的楊氏模量最小，隨著時間的推移，在應變不變的情況下，其應力波的傳播距離最小。③在5.64 μs時，各個模型應力波的傳播距離大，波形變化較明顯，其應力峰值比前兩個時間段小，層狀模型與單一介質模型波形曲線衰減規律趨于一致。但是，層狀模型應力峰值出現在2.75 cm處，即處于層狀模型中花崗巖介質的偏中部位置。這是由于當時應力波波前剛要通過分界面3，隨著應力波的擴散，其在模型邊界處形成的應力反射擾動與剛傳播至此位置處的應力波疊加。在2.67 μs時刻，存在同樣的規律。

6 結論

數值模擬表明，對于層狀巖性體模型，在“頁巖+玄武巖”分界面前后，反射波的加載作用導致入射應力峰值增大；透過分界面后，透射應力波以加載波的形成繼續傳播。在“玄武巖+花崗巖”分界面前后，應力峰值減小，同時，透射波應力擾動峰值小于入射波；在“花崗巖+大理巖”分界面前后，出現阻抗匹配現象，入射波幾乎以無反射的形式傳入大理巖介質，分界面前后其應力峰值幾乎相等。

不同的巖性單一介質模型，其應力波形變化規律是不同的。具體表現為：巖性楊氏模量越大，其應力波峰值出現得越早，應力波形衰減越快；不同巖性介質的波阻抗與應力峰值呈正相關。

對比單一介質模型與層狀模型可得，應力波在1.31 μs時，層狀模型應力峰值最大且變化范圍大，應力波傳播距離比任一單一介質模型都要??；在2.67 μs和5.64 μs時，應力峰值小于

單一介質模型，但其傳播距離要大于頁巖性單一介質模型。

巖石是典型的復雜介質，沖擊載荷下巖體中彈塑性波、粘彈性波以及三維介質中球面、柱面波的傳播特性還都有待深入研究。

參考文獻

[1]曹安業，竇林名，秦玉紅，等.微震監測沖擊地壓技術成果及其展望[J].煤礦開采，2007，12 （1）.

[2]李月.層狀巖體聲學特性研究[D].成都：西華大學，2007.

[3]王觀石，李長洪，陳保君，等.應力波在非線性結構面介質中的傳播規律[J].巖土力學，2009，30（12）.

[4]張奇.應力波在節理處的傳遞過程[J].巖土工程學報，1986，8（6）.

[5]陳虬，任輝啟.層狀介質中波傳播的彌散分析[J].西南交通大學學報，1998，33（1）.

[6]劉婷婷，李建春，李海波，等.應力波通過非線性平行節理的能量分析[J].巖石力學與工程學報，2013，32（8）.

[7]叢文相，孫豪志.二維層狀介質地震波速度的反演方法[J].石油地球物理勘探，1992，27（2）.

[8]董永香，馮順山，李學林.爆炸波在硬-軟-硬三明治介質中傳播特性的數值分析[J].彈道學報，2007，19（1）.

[9]趙堅，陳壽根，蔡軍剛，等.用UDEC模擬爆炸波在節理巖體中的傳播[J].中國礦業大學學報，2002，31（2）.

[10]劉彪，陸菜平，竇林名，等.震動波在煤巖介質中傳播特性的模擬研究[J].煤炭學報，2011，36（2）.

[11]C.HAN，C.T.SUN.Attenuation of stress wave propagation in periodically layered elastic media[J].Journal of Sound and Vibration，2001，243（4）.

[12]李夕兵，古德生.巖石沖擊動力學[M].長沙：中南工業大學出版社，1994.

[13]王禮立.應力波基礎[M].北京：國防工業出版社，2010.

[14]莊茁，由小川，廖建輝，等.基于ABAQUS的有限元分析和應用[M].北京：清華大學出版社，2009.

[15]鐘光復，王志亮，李永池.非均質巖體中一維應力波演化過程分析[J].中國工程科學，2006，8（5）.

〔編輯：劉曉芳〕