改進最大Lyapunov指數的多變量瓦斯濃度預測研究

張欣雨　李　茹,2　高俊杰　王　浩　王晉宇　趙紅燕

1(山西大學計算機與信息技術學院　山西 太原 030006)

2(山西大學計算智能與中文信息處理教育部重點實驗室　山西 太原 030006)

3(山西煤炭進出口集團科技發展有限公司技術管理處　山西 太原 030006)

4(太原科技大學計算機科學與技術學院　山西 太原 030024)

?

改進最大Lyapunov指數的多變量瓦斯濃度預測研究

張欣雨1李茹1,2高俊杰1王浩1王晉宇3趙紅燕4

1(山西大學計算機與信息技術學院山西 太原 030006)

2(山西大學計算智能與中文信息處理教育部重點實驗室山西 太原 030006)

3(山西煤炭進出口集團科技發展有限公司技術管理處山西 太原 030006)

4(太原科技大學計算機科學與技術學院山西 太原 030024)

摘要煤礦井下瓦斯濃度受到多個環境參數的影響。首先對煤礦井下同一時間段的瓦斯濃度、風速、壓力、溫度、CO2、O2的時間序列數據進行統計學相關性分析，選擇出對瓦斯濃度影響大的幾種因素，并作為基于最大Lyapunov指數改進預測模型的輸入參數來預測未來一段時間的瓦斯濃度。改進算法為：在用C-C方法重構多變量時間序列的相空間和Wolf方法計算最大Lyapunov指數的基礎上，同時考慮夾角余弦和歐氏距離求取預測中心點的相近點。結果表明，改進預測算法提高了預測精度，平均絕對誤差和標準差分別為2.11%和2.15%。

關鍵詞相關性分析最大Lyapunov指數C-C方法Wolf方法夾角余弦

STUDY ON IMPROVED MULTIVARIATE GAS CONCENTRATION PREDICTION BASED ON LARGEST LYAPUNOV EXPONENT

Zhang Xinyu1Li Ru1,2Gao Junjie1Wang Hao1Wang Jinyu3Zhao Hongyan4

1(School of Computer and Information Technology, Shanxi University, Taiyuan 030006,Shanxi,China)2(Key Laboratory of Computational Intelligence and Chinese Information Processing of Ministry of Education, Shanxi University, Taiyuan 030006,Shanxi,China)3(Shanxi Coal Import and Export Group Co,Ltd, Technology Management Office, Taiyuan 030006,Shanxi,China)4(School of Computer Science and Technology, Taiyuan University of Science and Technology, Taiyuan 030024,Shanxi,China)

AbstractThe gas concentration of coal mine is affected by lots of environmental parameters. First, we made the statistics correlation analysis on gas concentration, wind velocity, pressure, temperature, and the time series data of CO2and O2during the same period in coal mine, and selected some factors having big impacts on gas concentration as the input parameters of the improved prediction model, which was based on the largest Lyapunov exponent, to predict the gas concentration in coming period. The improved algorithm is that based on using C-C method to reconstruct the phase space of multivariate time series and using Wolf method to calculate the largest Lyapunov exponent, the cosine of angle and the Euclidean distance are taken into account at the same time to obtain the close points to the prediction centre point. Results showed that the improved prediction algorithm improved the prediction accuracy, its’ average absolute error and standard deviation were 2.11% and 2.15% respectively.

KeywordsCorrelation analysisLargest Lyapunov exponentC-C methodWolf methodCosine of angle

0引言

我國煤礦事故發生頻率相對較高，其中瓦斯災害是威脅我國煤礦井下安全生產的主要災害之一。因此對瓦斯有效準確的預測是預防瓦斯災害的關鍵。煤礦井下瓦斯濃度受到風速、溫度、煤層厚度、煤體地質結構等多個環境參數的影響，各種因素相互作用形成了復雜的煤巖瓦斯動力系統，采用傳統線性和非線性擬合方法很難對瓦斯濃度進行準確預測。因此，基于灰色系統理論[1]、混沌理論[2]、BP神經網絡理論[3]及多種組合理論[4,5]建立的非線性、多變量的瓦斯濃度預測模型逐漸成為研究熱點。

混沌理論是非線性動力系統普遍存在的運動形式，而最大Lyapunov指數作為判斷混沌系統內在規律性的重要參數，其算法及改進算法被廣泛應用于混沌時間序列的預測問題[6-9]。但現有最大Lyapunov預測模型多考慮單變量時間序列，而煤礦井下復雜系統的動態演化是由多種因素綜合影響的，并且單變量攜帶信息存在很大的局限性。因此，建立基于最大Lyapunov指數的多變量瓦斯濃度預測模型具有實際意義。另外，針對預測中心點的軌道與通過歐式距離求得的它的最鄰近點的軌道可能并非最優的問題，本文引入了Wolf方法計算最大Lyapunov指數時，同時考慮夾角余弦和距離來求取鄰近點的思想來改進算法。

1煤礦井下多環境因素數據處理

盡管綜合考慮煤礦井下多個環境參數利于對瓦斯濃度進行準確預測，但也增加了計算量和冗余度。本文首先對數據進行歸一化處理，然后用統計學上的相關性分析法找到與瓦斯關聯度大的因素，然后再建立相應模型進行預測，這樣既能考慮到多變量影響又能減少冗余度。公式為：

(1)

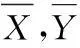
2基于混沌理論的多變量瓦斯濃度預測模型

2.1多變量時間序列的相空間重構

混沌是復雜動力系統普遍存在的一種特有狀態，系統中任一分量的演化是系統中其他要素相互作用的結果，該分量包含著動力系統在多自由度空間中的信息。Takens[10]等人提出并證明若能找到某一變量合適的嵌入維，可用該變量的延遲坐標重構相空間來恢復動力系統的規律。而單一變量攜帶信息具有一定的局限性，因此考慮用多變量來重構煤礦井下動力系統的相空間[11]。嵌入維m和時間延遲τ在相空間重構時是比較重要的參數。若τ太小，則坐標相關性太強，會造成信息冗余；若τ太大，則會導致信息丟失。m太大，則增加噪聲干擾，同時加大了運算量。參數選擇不當會直接影響重構后的相空間與原空間的同胚關系。大量文獻表明，m和τ具有關聯性[12-14]。本文采用簡化的C-C方法，關聯求取這兩個參數。

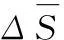
設X1,X2,…,XN為N類時間序列，對第i類時間序列有Xi=(xi,1,xi,2,…,xi,Q)，i=1, 2,…,N，Q為數據個數，則進行多變量相空間重構后的相點為：

Yp=(x1,p,x1,(p-τ1),…,x1,(p-(m1-1)τ1),x2,p,x2,(p-τ2),…，

x2,(p-(m2-1)τ2),…，xN,p,xN,(p-τN),…,xN,(p-(mN-1)τN))

(2)

2.2Lyapunov指數及其改進預測算法

對重構后多變量形成的時間序列進行混沌性識別，是驗證能否用混沌理論進行多變量瓦斯濃度預測的關鍵。Lyapunov指數具有描述重構相空間中相近軌道的平均指數發散率的性質，是判斷系統是否具有混沌性的參數，能從本質上揭示系統內在的演化規律，可作為對下一相點進行預測的參數，同時能量化最大預報時長[15]。常見計算最大Lyapunov指數的方法[16]有定義法、Wolf方法、小數據量法、Jacobian方法、正交法等。本文采用Wolf方法，設λ為求取的最大Lyapunov指數，則最大預報時長為Tl=1/λ[17]，改進求取預測中心點的鄰近點方法如下：

(1) 計算相空間中任意兩點間的最短平均距離L0作為鄰近點求取時的變化尺度：

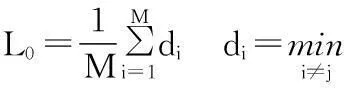
(3)

(4)

其中‖·‖為歐式距離。

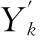
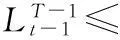
(5)

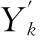
(6)

圖1　Wolf方法求鄰近點示意圖

通過上述算法，得出預測中心點YM的最鄰近點為Yk，根據Lyapunov指數具有指數發散性的性質，經過p步演化后，有：

‖YM+p-Yk+p‖=eλp‖YM-Yk‖

(7)

式中，若p≤t，t=max(τi),i=1,2,…，N，則YM+p只有一個分量xM+p,(mt-1)τt是未知的，那么可得p步后多變量瓦斯濃度預測公式：

xM+p,(mt-1)τt=xk+p±

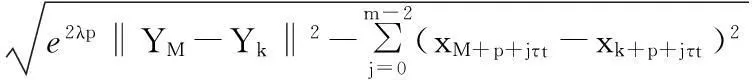
(8)

2.3改進最大Lyapunov指數瓦斯濃度預測流程

根據上述理論，采集山西省屬于高瓦斯的某煤礦對多種環境因素的實時監測數據進行分析，模擬未來時刻瓦斯濃度的變化，流程如圖2所示。

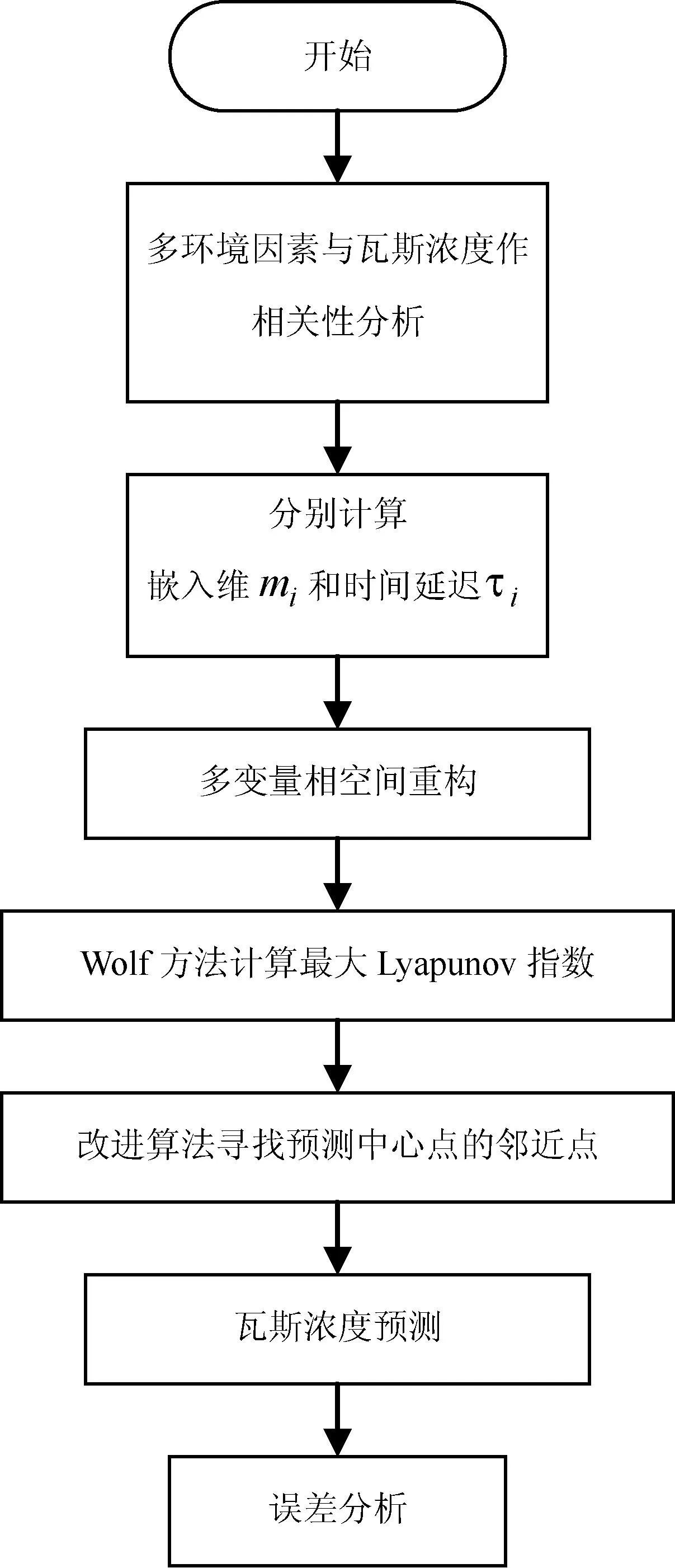
圖2　基于最大Lyapunov指數的改進瓦斯濃度預測流程

3實驗及分析

由《山西省煤礦數據采集標準(C)》的規定，實時監測數據每間隔30s上傳一次。考慮到龐大、緊密的數據存在一定數據冗余，因此，隨機抽取多種環境因素各10 000條連續的分鐘數據進行仿真實驗。首先用SPSS軟件對瓦斯濃度、風速、壓力、溫度、CO2、O2進行典型相關性分析，如表1所示。

表1　瓦斯濃度及各因素相關性分析

圖3　C-C方法求三類時間序列的m和τ時對應的(t)

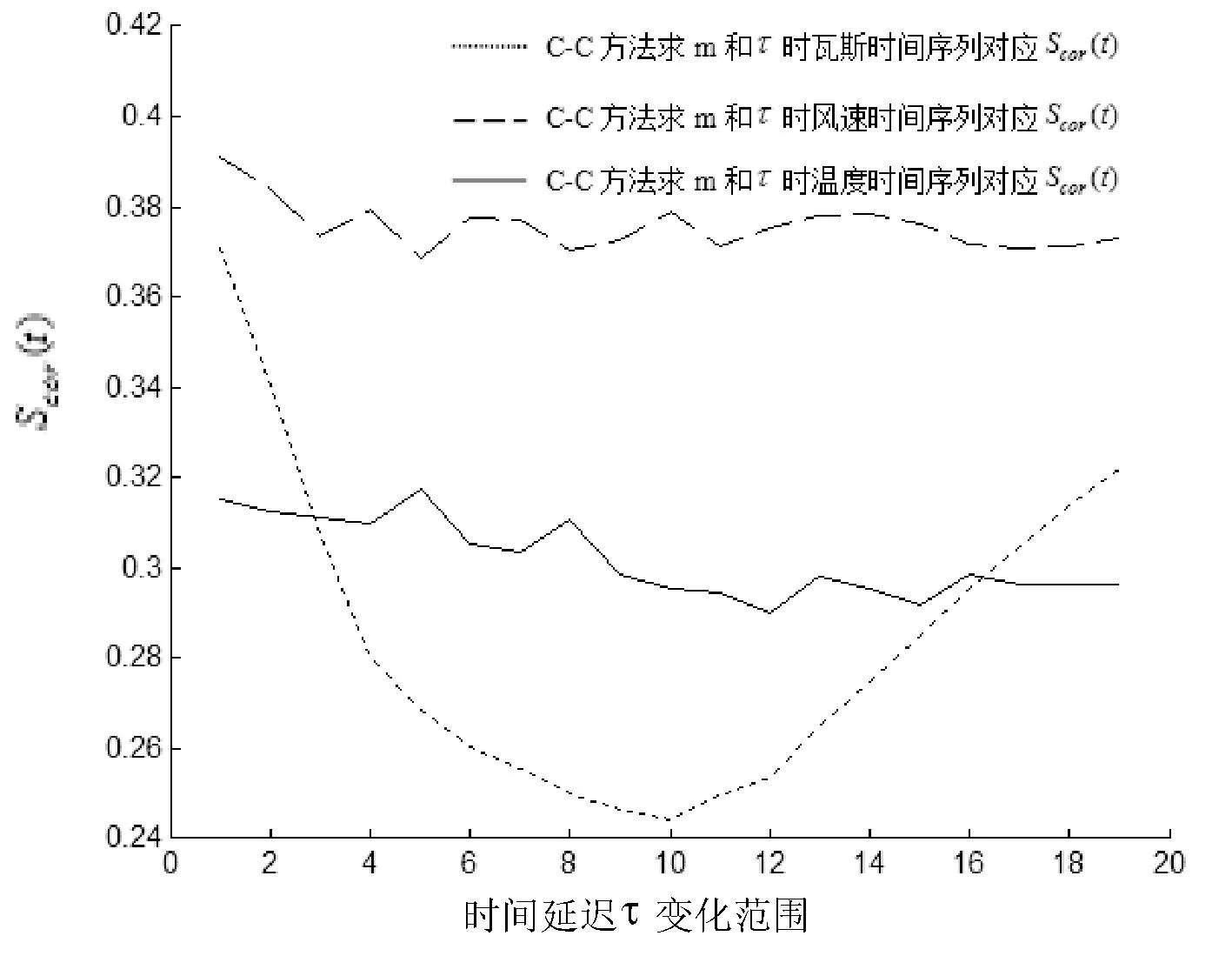
圖4　C-C方法求三類時間序列的m和τ時對應的Scor(t)

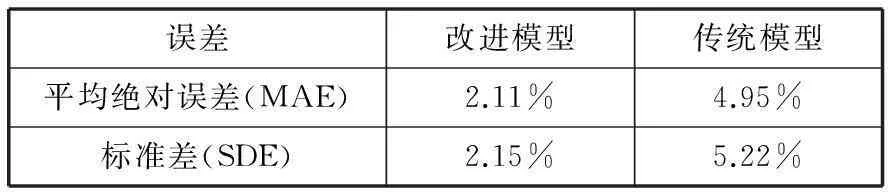
表2　改進前后瓦斯濃度預測誤差對比表

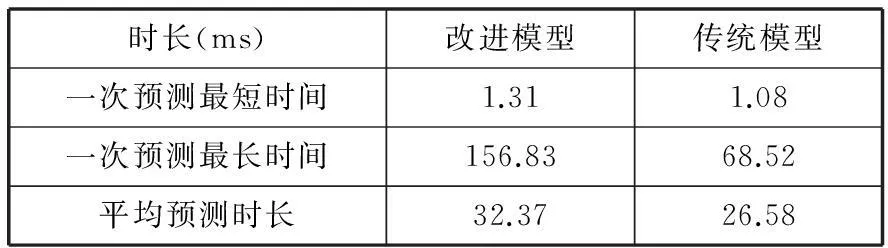
表3　改進前后算法執行效率對比表

圖5　改進前后瓦斯濃度預測對比圖

從表2可以看出，基于改進后最大Lyapunov指數的多變量瓦斯濃度預測模型的MAE和SDE分別為2.11%、2.15%，較傳統模型低，改進算法提高了預測精度。從表3可以看出，改進算法的一次預測執行最短時間和最長時間及平均時長比傳統算法耗時稍長，因為改進算法每次預測都要同時考慮歐式距離和夾角余弦來求預測點的最鄰近點，這在一定程度上增加了比較次數和運算量。如果通過距離和夾角余弦與僅通過距離求得的鄰近點是相近的，則運算時長會比較接近。由表3可知預測平均

耗時比較接近，由表2可知改進算法的精度有了提高，說明改進算法在瓦斯濃度預測上是有效的。

4結語

本文首先對煤礦井下的多環境因素與瓦斯濃度作統計學意義上的相關性分析，找到與瓦斯濃度關系密切的因素，然后用簡化的C-C方法重構多變量時間序列的相空間和Wolf方法計算最大Lyapunov指數，并通過考慮夾角余弦和歐氏距離來對基于最大Lyapunov指數預測多變量瓦斯濃度的算法進行了改進。實驗表明，改進預測模型的精確度優于傳統模型，且能及時準確地預測未來近15 min后的瓦斯濃度，可為井上煤礦安全管理人員提供分析和決策依據，并有足夠的時間采取加大通風量、疏散工人等措施，具有一定的使用價值。接下來，可探討是否能與實際接軌，結合煤礦多種地質因素來進一步改善模型，并最終應用到生產實際。

參考文獻

[1] 王文才,李剛,張世明,等.基于灰色理論的礦井瓦斯涌出量預測研究[J].煤礦開采,2011,16(3):56-58.

[2] 趙志剛,譚云亮.基于混沌理論的煤與瓦斯突出前兆時序預測研究[J].巖土力學, 2009,30(7):2186-2189.

[3] 趙延明.基于改進BP神經網絡的瓦斯含量預測模型[J].工礦自動化,2009(4):10-13.

[4] 谷松,崔洪慶,馮文麗.基于灰色理論的小波神經網絡對瓦斯涌出量的預測[J].煤炭學報,2007,32(9):964-966.

[5] 付華,舒丹丹,荊曉亮.基于MPSO-RBF的瓦斯涌出量預測研究[J].計算機測量與控制,2012,20(10):2625-2627.

[6] 張文超,譚思超,高璞珍.基于Lyapunov指數的搖擺條件下自然循環流動不穩定性混沌預測[J].物理學報,2013,62(6):1-8.

[7] 胡誠皓,楊啟林,邵定宏.基于改進最大Lyapunov指數求解的成本預測方法[J].計算機工程與設計,2008,29(18):4825-4827.

[8] 吳華穩,王富章.基于最大Lyapunov指數的鐵路貨物運量預測研究[J].鐵道學報,2014,36(4):7-13.

[9] 黃文標,施式亮.基于改進Lyapunov指數的瓦斯涌出量時間序列預測[J].煤炭學報, 2009,34(12):1665-1668.

[10] Takens F. Determing strange attractors in turbulence[J].Lecture Notes in Math, 1981,898(2):361-381.

[11] 趙志剛,譚云亮. 基于混沌理論的煤與瓦斯突出前兆時序預測研究[J].巖土力學,2009,30(7):2186-2190.

[12] 張寶燕,李茹,穆文瑜.基于混沌時間序列的瓦斯濃度預測研究[J].計算機工程與應用,2011,47(10):244-248.

[13] 韓曉霞,謝剛,韓曉明,等.基于相空間重構和支持向量機的多相催化劑失活預測[J].控制與決策,2012,27(6):953-960.

[14] 黃謙,李天偉,楊邵清,等.船舶航行數據的相空間重構及混沌特性分析[J].計算機應用,2011,31(11):3157-3164.

[15] 葛軍偉,任偉,方義秋.基于最大Lyapunov指數的軟件失效預測[J].計算機應用與軟件,2013,30(3):114-117.

[16] 張海龍,閔富紅,王恩榮. 關于Lyapunov指數計算方法的比較[J].南京師范大學:工程技術版,2012,12(1):5-9.

[17] 趙明,梁平,龍新峰.基于最大Lyapunov指數對腐蝕深度的預測[J].機械工程學報,2008,44(1):217-221.

中圖分類號TP391.9

文獻標識碼A

DOI:10.3969/j.issn.1000-386x.2016.02.016

收稿日期：2014-08-03。太原市創新成果惠及民生專項(120 231)；太原市科技創新項目(110263)。張欣雨，碩士生，主研領域：智能信息處理。李茹，教授。高俊杰，助理實驗師。王浩，本科。王晉宇，高工。趙紅燕，講師。