基于ROAD和小波收縮的MLEM低劑量CT重建算法

董嬋嬋　桂志國　張　權　郝慧艷　張　芳　劉　祎　孫未雅

(中北大學信息與通訊工程學院　山西 太原 030051)

?

基于ROAD和小波收縮的MLEM低劑量CT重建算法

董嬋嬋桂志國張權郝慧艷張芳劉祎孫未雅

(中北大學信息與通訊工程學院山西 太原 030051)

摘要針對低劑量CT (Computed Tomography)重建圖像質量退化的問題，提出一種基于小波收縮和絕對差值排序各項異性擴散的MLEM(Maximum Likelihood Expectation Maximization)低劑量CT重建算法。算法在每次迭代中首先采用MLEM算法對低劑量CT投影數據進行重建。由于各項異性擴散對噪聲敏感，所以算法先對重建后的圖像進行小波變換，再在更穩定的低頻小波域進行基于絕對差值排序的各項異性擴散處理，對小波高頻系數進行軟閾值降噪處理。然后將降噪處理后的系數進行小波反變換，得到降噪后的圖像。最后使用中值濾波對圖像進行處理，從而消除脈沖噪聲點。實驗結果表明，與其他幾種常用重建算法相比，該算法重建的圖像信噪比更高，歸一化均方誤差更小，處理后的圖像更清晰，即可以在抑制噪聲的同時，較好地保持圖像的邊緣和細節信息。

關鍵詞低劑量CT小波變換圖像重建絕對差值排序各向異性擴散

MLEM LOW-DOSE CT RECONSTRUCTION ALGORITHM BASED ON ROAD AND WAVELET SHRINKAGE

Dong ChanchanGui ZhiguoZhang QuanHao HuiyanZhang FangLiu YiSun Weiya

(School of Information and Communication Engineering, North University of China, Taiyuan 030051,Shanxi,China)

AbstractConcerning the problem of quality degradation of low-dose CT reconstruction images, we presented an MLEM low-dose CT reconstruction method which is based on wavelet shrinkage and rank-ordered absolute differences anisotropic diffusion. In each time of iteration, the algorithm first uses MLEM to reconstruct the low-dose projection data. Since the anisotropic diffusion is sensitive to noises, so the algorithm performs wavelet transform on the reconstructed image prior to conducting anisotropic diffusion processing based on rank-ordered absolute differences in more stable low-frequency wavelet domain and then carries out the soft threshold denoising processing on high-frequency coefficient of wavelet. After that the algorithm performs inverse discrete wavelet transform (IDWT) on the coefficients with denoising treatment and obtains the denoised images. Finally it uses median filter to process the image so as to eliminate the impulse noise points. Experimental results showed that compared with some other common reconstruction algorithms, the image reconstructed by the proposed one had higher signal-to-noise ratio (SNR) and smaller normalised mean square error, the processed image with the proposed algorithm were much clear, i.e., it could well preserve edges and details information of image while suppressing the noise.

KeywordsLow-dose computed tomography (CT)Wavelet transformImage reconstructionRank-ordered absolute differences (ROAD)Anisotropic diffusion

0引言

計算機斷層成像術CT技術在疾病預防、臨床診斷中發揮了巨大的作用[1]。然而，因其較高的輻射劑量會對人體造成一定的傷害，所以在掃描時應盡可能地降低射線劑量，即采用低劑量CT成像技術[2]。低劑量CT可減少對受檢者的放射危害，然而當劑量降低時，由于穿過人體抵達探測器的光子數目過少，投影數據會被隨機噪聲嚴重污染，導致重建得到的圖像質量退化明顯，重建圖像中可見明顯的條狀偽跡。因而，有效地濾除低劑量CT圖像的噪聲，有著重要的實際應用價值。

到目前為止，人們已經提出了很多濾波策略來解決噪聲問題，主要包括在投影域進行統計濾波并用濾波反投影算法重建圖像和在CT重建圖像域直接去噪的算法。目前在投影域進行濾波的研究工作主要包括：Kachelriess M等人[3]提出了一種投影域的自適應卷積濾波方法；畢一鳴等人利用噪聲的統計特性[4]，提出了一種基于標準劑量CT圖像非局部權值先驗的低劑量圖像恢復方法； Gui Zhiguo[5]等根據低劑量CT噪聲的特性，提出一種模糊中值濾波器，用此對低劑量CT的投影數據進行降噪處理，從而提高圖像的抗噪聲性能；劉祎[6]等通過使用局部模糊熵判斷細節和平滑區域，然后利用基于統計信息的各向異性濾波作用在投影數據中，從而得到高信噪比的恢復圖像。由于在投影域降噪后，即使遺留下很小的點噪聲，映射到圖像域也會形成條形偽影。因此，在重建后的圖像上進行去噪的算法得到了廣泛關注。Chen Yang[7]等通過使用非局部自適應加權先驗統計方法進行圖像重建，改善了低劑量CT圖像的質量。王麗艷[8]等通過采用待重建圖像稀疏性的先驗信息作為正則項，泊松噪聲的負對數似然函數作為保真項設計優化目標函數，從而達到去噪且保持細節的目的。Rust 等利用非線性高斯濾波器鏈對重建圖像進行平滑處理[9]，得到不錯的降噪效果且很好地保持了邊緣和細節。Lui D[10]提出一種新穎的噪聲補償CT重建方法從而提高了重建圖像的信噪比。

目前圖像降噪的方法有很多，如：數學形態學法、小波技術[11，12]、非局部均值濾波法[13]以及基于偏微分方程的圖像降噪算法法[14，15]。近年來，基于小波變換和基于偏微分方程的圖像處理方法受到人們的廣泛關注。通過以上研究分析，本文提出了一種基于小波和絕對差值排序ROAD(rank-ordered absolute differences)各項異性擴散的最大似然期望最大化MLEM的低劑量CT重建算法。該算法先對投影數據進行重建，在將重建得到的圖像進行小波分解，對高頻系數進行閾值降噪處理，對小波低頻系數進行基于ROAD的各項異性擴散。實驗結果表明，該算法重建出來的圖像可以在對圖像進行降噪的同時，較好地保持圖像的邊緣和細節信息。

1噪聲模型

關于投影數據噪聲模型的數據特點已經進行了廣泛的研究，文獻[16]認為探測到的光子數服從背景噪聲為高斯噪聲的泊松分布。Lu等人通過對多個體模進行反復掃描獲得的投影數據進行分析得出[17，18]：經系統校準及對數變換之后的低劑量CT投影數據近似服從非平穩高斯分布，且其均值和方差之間具有非線性關系。其統計模型為：

σi2=kiexp(λi/T)

(1)

其中，i=1,2,…,N表示探測器信道，N表示信道總數，λi表示第i個探測器獲得投影數據的均值，σi2表示第i個探測器獲得投影數據的方差，ki表示第i個探測器的參數，T表示用于描述掃描系統校準過程的系統參數。對于給定的CT采集系統，ki與T是給定的。

2基于絕對差值排序和小波收縮的MLEM低劑量CT重建算法

2.1MLEM重建方法

MLEM算法由于在重建過程中考慮了觀測數據的統計特性，使重建出的圖像優于FBP重建出的圖像，重建公式如下：

(2)

2.2本文算法的理論知識

2.2.1基于絕對差值排序的各項異性擴散

P-M方程的表達式為：

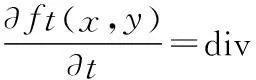
(3)

其中ct為擴散系數函數，其表達式為：

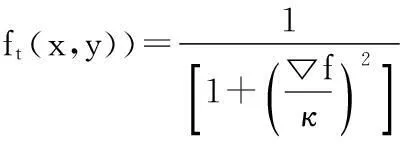
(4)

由于有些噪聲的梯度值與邊緣的梯度值相差無幾，甚至更大，因此只依靠梯度信息來檢測邊緣是不夠的。文獻[15]指出：即使在噪聲與邊緣的梯度值相似時，噪聲與邊緣處的灰度方差卻相差很大，細節處的灰度方差明顯比噪聲處的灰度方差大。Chao和Tsai在P-M模型的基礎上增加了灰度方差的信息，可以在去除噪聲的同時保留更多的細節。

通過在擴散過程中包含梯度和灰度方差的局部特征，式(4)中的擴散系數函數改為：

(5)

為了表示出某個特定的像素值與它周圍的鄰域像素值強度的差異，Roman Garnett等人[19]提出了一個局部圖像統計—絕對差值排序檢測法ROAD。設中心像素點的坐標為x=(x1,x2),則：

Ωx(N):={x+(i,j):-N≤i,j≤N}

(6)

(7)

由于圖像的內部區域及邊緣都具有連續性，所以在它周圍的八鄰域中，至少有四個鄰域值與中心像素的強度相似，說明其ROAD值較小。而噪聲會使中心像素與大多數或所有的鄰域像素在強度上相差很大，說明ROAD值較大。因此，通過ROAD值的大小可以區分出邊緣與噪聲。此時，擴散系數函數的表達式為：

(8)

基于絕對差值排序的各項異性擴散方程的離散化形式為：

ft+1(x,y)=ft(x,y)+

(9)

2.2.2小波降噪

圖像降噪的目的是為了改善圖像質量，減少噪聲，同時盡可能保持圖像的特征不被破壞。由于噪聲和圖像的特征都是高頻成分，因此在降噪的同時會損失圖像的細節特征。近年來，在圖像去噪領域，小波理論受到了許多學者的重視，將小波應用到降噪領域，獲得了非常好的效果。其中，小波閾值收縮法是目前研究最為廣泛的小波去噪算法。由于小波系數在層間存在較強的持續性，小波域中信號系數隨著尺度的增加而增加[20]，而噪聲系數隨著尺度的增加而減小。因此將信號進行小波分解后，高頻小波系數中絕對幅值比較大的小波系數主要由真是圖像信號提供，予以保留；絕對幅值比較小的小波系數主要由噪聲提供，濾除這樣的系數就可達到降噪效果。

f(k)=s(k)+n(k)k=0,1,2,…，N-1

(10)

對f(k)做離散小波變換，可得：

wf(j,k)=ws(j,k)+wn(j,k)

(11)

其中，wf(j,k)、ws(j,k)和wn(j,k)分別表示包含噪聲信號、原始信號和噪聲信號在第j層上的小波系數。

2.3算法描述

一方面，圖像經過小波變換后，邊緣和噪聲是高頻分量，圖像的主要信息都集中在低頻部分。由于各項異性擴散對噪聲較敏感，而低頻分量中的噪聲較少，因此在低頻部分進行各項異性擴散可以減小噪聲對其的影響。另一方面，小波收縮去噪方法是對小波系數進行統一處理，同時考慮了小波系數之間的相關性和局部特征。非線性擴散方法與像素點的具體位置有關[21]，它是一種從局部向整體逐漸擴散的過程。但是這種方法需要多次迭代，計算量較大，相比之下，小波收縮的速度較快。由于小波收縮方法收斂速度快，所以在高頻分量部分采用小波收縮軟閾值去噪；從計算復雜性考慮，由于圖像經過一次小波變換后，低頻部分大小減為原始圖像的1/4。所以，圖像經過多尺度分解后，低頻部分大小遠小于原圖像大小，因此只對低頻部分采用非線性濾波，比在整幅圖中采用非線性濾波所用的時間大大減少。因此，本文算法的降噪部分采用混合圖像去噪算法。

算法先對投影數據進行重建，然后將重建后的圖像進行小波分解，使得圖像的主要信息大都集中在低頻，圖像的邊緣和噪聲大都集中在高頻。再對信號的低頻小波系數進行各項異性擴散處理，減少噪聲對各項異性擴散的影響；對小波域中信號的高頻系數進行軟閾值處理。將降噪處理后的小波系數進行小波反變換，最后再對降噪后的圖像進行中值濾波處理。由于噪聲和邊緣都是高頻信息，但在小波域中信號小波系數隨著尺度的增加而變大，而噪聲系數隨著尺度的增加而減小，所以通過軟閾值處理可以有效去除噪聲。由于圖像的信息主要集中在低頻，低頻中包含的噪聲較少，因此本文將差分曲率算子引入到各項異性擴散方程中，對低頻信息進行小幅度的平滑處理，去除低頻中的噪聲。根據上述分析，本文算法的流程如圖1所示。

本文根據圖1中的流程可知該算法的具體步驟如下：

(2) 在每次重建迭代中，首先對上步重建后的圖像信號進行多尺度小波變換，生成相應的低頻分量CAi，高頻分量CHi,CVi,CDi，i=1,2,…,n為分解尺度。

(3) 然后，對高頻系數進行軟閾值處理，去除噪聲；對低頻系數用基于絕對差值排序檢測各項異性擴散算法進行圖像降噪處理。

閾值處理過程分為軟閾值和硬閾值，硬閾值方法可以很好地保留圖像邊緣等局部特征，但圖像會出現振鈴、偽吉布斯效應等視覺失真，而用軟閾值方法處理結果則相對平滑得多。因此，本文采用軟閾值方法。

(4) 在小波域進行圖像降噪處理后，進行小波反變換得到去噪后的圖像。

(5) 對各向異性擴散處理后的脈沖噪聲進行中值濾波處理：

fi,jn + 1=Median(fi,jn + 1,w)，

其中，w是中值算子的窗口。

圖1　本文算法流程圖

由文獻[22]可知，低劑量CT重建圖像的噪聲還表現為一些脈沖噪聲，各向異性擴散降噪技術對重建的圖像進行降噪后，僅可以平滑圖像的小梯度區域，而相對于周圍區域的大梯度區域則保持不變，這些大梯度可能是邊緣，也可能是圖像的峰值噪聲。而中值濾波器只會對大噪聲峰值產生的大梯度起作用，邊緣產生的大梯度將不會受到影響。因此在低劑量CT重建時，低噪聲可以由各向異性擴散平滑，而大噪聲等脈沖噪聲則由中值濾波器所消除。

即采用各項異性擴散降噪算法對重建圖像進行處理后，小噪聲引起的小梯度區域被平滑，而大噪聲峰值如脈沖噪聲由該中值濾波進行濾除。由于中值濾波是將窗口內像素的灰度值進行排序，用排序所得的中間值代替窗口中心位置像素的灰度值，若窗口選擇太大會使計算量過大，運行時間過長，不利于圖像處理的實時性，因此這里w取3×3的窗口。

(6) 重復步驟(1)-(5)直至得到最終的重建圖像。

先對投影數據進行MLEM重建，然后進行圖像域降噪處理。降噪部分即先進行基于小波收縮和絕對差值排序各項異性擴散，然后進行中值濾波。

F=(F.*(ggg*(p2./(G*F))));

%MLEM重建方法

g=reshape(F,128,128); x=double(g); xx=x;

[swa,swh,swv,swd] = swt2(xx,3,′db1′);

%采用db1進行多尺度小波分解

[thr] = ddencmp(′den′,′wv′,xx);

%對高頻部分進行小波軟閾值處理

sorh = ′s′; dswh = wthresh(swh,sorh,thr);

dswv = wthresh(swv,sorh,thr);

dswd = wthresh(swd,sorh,thr);

h=0.8; k=swa(:,:,3);

%對低頻部分進行基于ROAD的各項異性擴散降噪處理

scalval=0.085; kval=1; x=5;

he=fspecial(′gaussian′, 3, 9);

imgMean1=imfilter(k,he);

imgMean=imfilter(k,he);

for ii=2:N-1

for jj=2:M-1

for iii=ii-1:ii+1

for jjj=jj-1:jj+1

sigma(ii,jj)=(k(iii,jjj)-imgMean(ii,jj))*(k(iii,jjj)-imgMean(ii,jj));

end

end

sigma(ii,jj)=sigma(ii,jj)/9;

end

end

sigma=1+(sigma-min(sigma(:)))/(max(sigma(:))-min(sigma(:)))*254;

for ii=2:N-1

for jj=2:M-1

B=zeros(3,3);

a1=abs(k(ii-1,jj)-k(ii,jj));

a2=abs(k(ii,jj-1)-k(ii,jj));

a3=abs(k(ii+1,jj)-k(ii,jj));

a4=abs(k(ii,jj+1)-k(ii,jj));

a5=abs(k(ii+1,jj-1)-k(ii,jj));

a6=abs(k(ii+1,jj+1)-k(ii,jj));

a7=abs(k(ii-1,jj-1)-k(ii,jj));

a8=abs(k(ii-1,jj+1)-k(ii,jj));

A=[a1,a2,a3,a4,a5,a6,a7,a8];

B=sort(A);

ROAD=B(1)+B(2)+B(3)+B(4); kkk=0;

tidu=k(ii-1,jj)-k(ii,jj); tidu1=tidu; kk1=tidu*(x*ROAD*kval*kval)/((x*ROAD*kval*kval)+sigma(ii,jj)*sigma(ii,jj)*tidu1*tidu1+eps);

tidu=k(ii,jj+1)-k(ii,jj); tidu1=tidu; kk2=tidu*(x*ROAD*kval*kval)/((x*ROAD*kval*kval)+sigma(ii,jj)*sigma(ii,jj)*tidu1*tidu1+eps);

tidu=k(ii+1,jj)-k(ii,jj); tidu1=tidu; kk3=tidu*(x*ROAD*kval*kval)/((x*ROAD*kval*kval)+sigma(ii,jj)*sigma(ii,jj)*tidu1*tidu1+eps);

tidu=k(ii,jj-1)-k(ii,jj); tidu1=tidu; kk4=tidu*(x*ROAD*kval*kval)/((x*ROAD*kval*kval)+sigma(ii,jj)*sigma(ii,jj)*tidu1*tidu1+eps);

kkk=kk1+kk2+kk3+kk4;

k(ii,jj)=k(ii,jj)+kkk*scalval;

end

end

swa(:,:,3)=k;

xd=iswt2(swa,dswh,dswv,dswd,′db1′);

%小波反變換

g=reshape(xd,128,128);

g=medfilt2(g);

%中值濾波

F=reshape(g,16384,1);

3實驗結果與分析

為了驗證算法的有效性，本文采用Sheep-Logan體模作為實驗模型進行低劑量CT圖像重建的仿真，與BIPLS(Block Iterative-Penalized Least Squares)，OS-PML-OSL(Ordered Subsets-Penalized Maximum Likelihood-One Step Late)進行了比較，且為了進一步說明本文中改進各向異性擴散算法在MLEM的低劑量CT重建算法的有效性，將基于傳統PM、基于方差應用到MLEM算法中，并和本文算法進行了比較。采用大小為128 mm×128 mm，灰度為0~255的Sheep-Logan頭部體模。實驗通過在360°范圍內均勻選取984個投影角度，每個投影角度下有888條射線的方法來獲得仿真的無噪聲投影數據。在此基礎上，按照式(1)的方法向理想投影數據中加入高斯噪聲來模擬低劑量CT的投影數據，其中ki=200，T=12 000。實驗仿真環境為：32位Microsoft Windows XP Professional 2002計算機操作系統，E5300@2.60 GHz英特爾奔騰雙核處理器 ，2 GB內存。軟件環境為：MATLAB R2008a。圖2為不同算法重建的圖像。

圖2　各種算法的對比結果

圖2(a)為原始圖像。(b) 采用OS-PLS重建算法。(c) 采用OS-PML-OSL重建算法。(d) 使用MLEM算法進行重建，然后采用基于傳統PM的各向異性擴散對圖像域進行降噪。(e) 使用MLEM算法進行重建，然后采用基于方差的各向異性擴散對圖像域進行降噪。(f) 采用本文提出的算法。

由圖2(b)可以明顯看出，MLEM重建算法的重建結果圖中含有較多噪聲，重建效果不好。(c)和(d)與(b)相比可以看出：算法BIPLS和OS-PML-OSL比(b) MLEM算法重建后的圖像包含更少的噪聲，重建效果較好。而(e)比(b)、(c)和(d)中包含更少的噪聲，重建的圖像更清晰。將(f)的結果與(b)、(c) 、(d) 和(e)相比可以明顯看出：與其他四種算法的重建結果相比，本文提出算法的重建圖像更清晰，包含的噪聲更少。綜上所述，本文算法可以有效地解決低劑量重建圖像的噪聲問題，且可以在光滑去噪的同時較好地保持圖像的紋理和邊緣信息。

圖3(a)為一個大小為128 mm×128 mm的肩部仿真模型，(b)為MLEM重建后的結果，(c)為BIPLS算法處理后的結果，(d)為OS-PML-OSL處理后的圖像，(e)為基于方差的MLEM處理后的結果，(f)為本文算法處理后的結果。

由圖3可以清晰看出，圖像(f)較清晰，圖像質量較高，即本文處理后的圖像明顯優于其他算法處理后的圖像。因此，本文算法可以有效地解決低劑量重建圖像的噪聲問題，且可以在光滑去噪的同時較好地保持圖像的紋理和邊緣信息。總之，從視覺上來看，重建效果優于其他幾種比較算法。

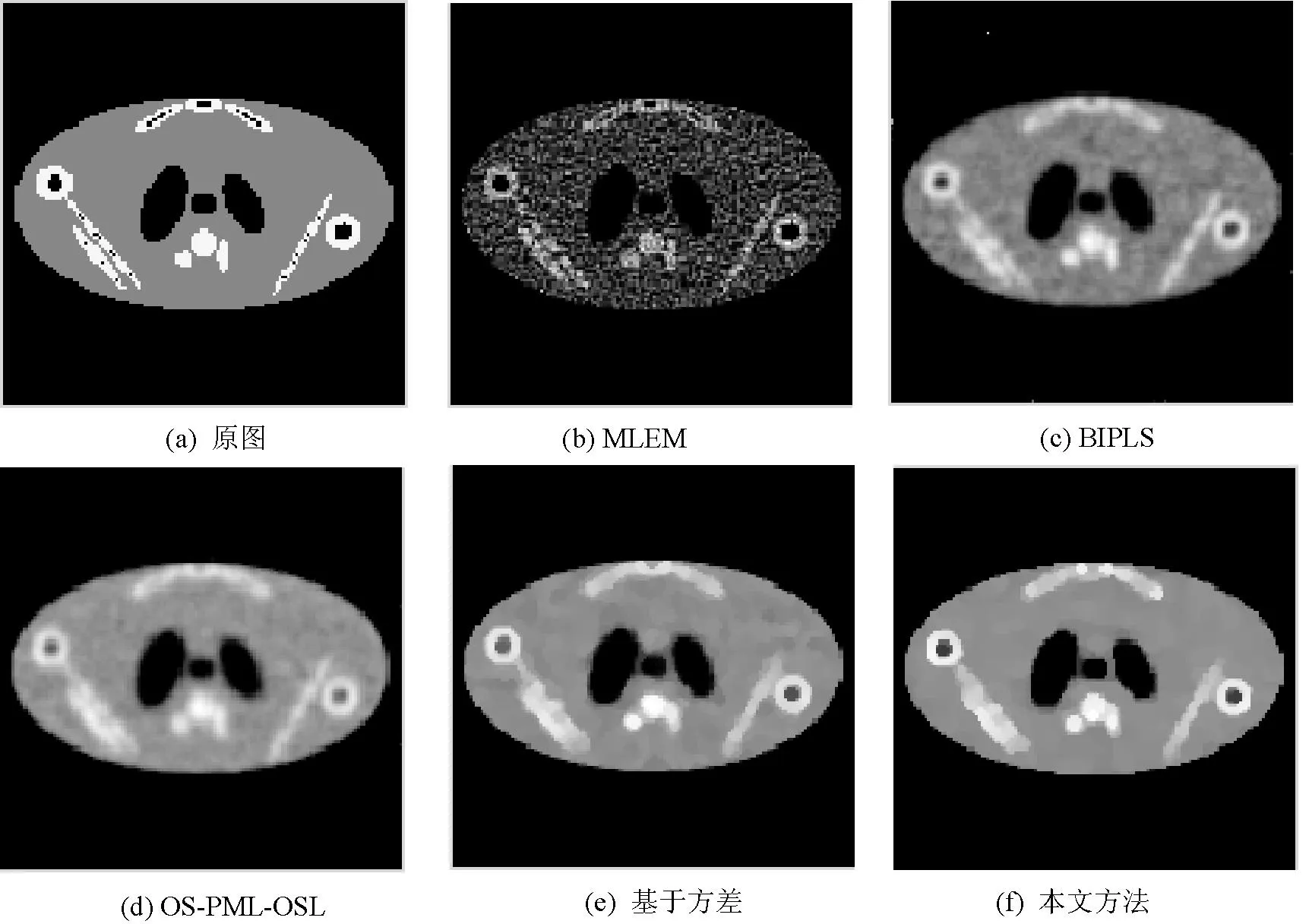
圖3　各種算法的對比結果

從上述分析可得，本文提出的算法在去噪能力與保持邊緣和細節能力方面都明顯優于其他重建方法。為了進一步證明本文算法的有效性，本文采用歸一化均方距離、歸一化均方誤差、均方絕對誤差、信噪比對其進行定量描述。其定義分別如下：

(1) 歸一化均方距離NMSD:

(12)

(2) 歸一化均方誤差NMSE:

(13)

(3) 均方絕對誤差MAE:

(14)

(4) 信噪比SNR:

(15)

其中，M和N分別為圖像的行數和列數，Fi和fi分別表示重建圖像與原始圖像的第i個像素的灰度值，Mi和mi分別表示重建圖像與原始圖像的均值，本文提出的新算法以及各種比較算法關于Sheep-Logan體模仿真的客觀評價結果如表1所示。

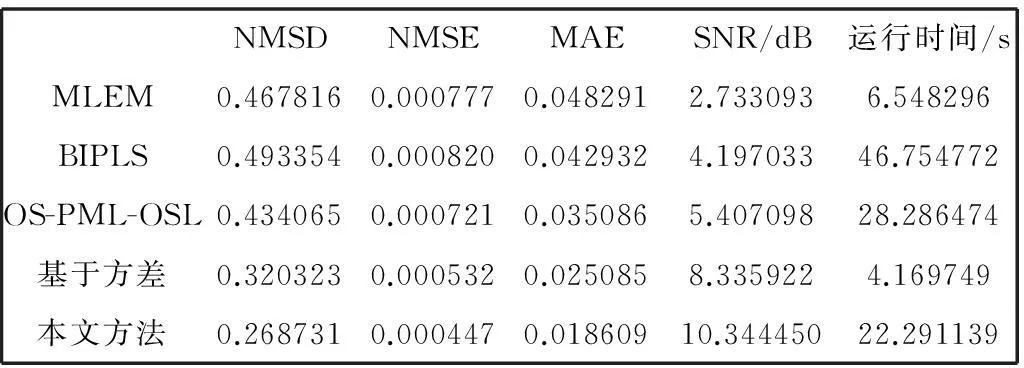
表1　各種算法的客觀評價

由表1可以明顯看出，本文提出算法的歸一化均方誤差NMSE、歸一化均方距離NMSD、均方絕對誤差MAE均比其他的幾種比較算法小，信噪比SNR高達10.344450，比其他幾種算法高出很多。因此由圖2和表1可知，無論在視覺方面還是在定量評價方面，均表明本算法在CT重建中是可行且有效的。

圖4給出了Sheep-Logan體模的以上重建圖像與原始理想圖像的側面輪廓線的比較圖。從圖中可以看出本文算法對低劑量進行CT重建更為接近理想圖像，與原始圖像的吻合度最高，即和其他幾種比較算法相比較，本文方法重建出的圖像噪聲波動最小，可以較好地去除低劑量CT圖像的噪聲以及較好地保持圖像的細節和紋理信息。

圖4　各種算法第65行側面輪廓線的對比結果

4結語

本文提出了一種基于絕對差值排序各項異性擴散和小波收縮的MLEM的低劑量CT重建算法。各項異性擴散雖然可以有效去除圖像的噪聲，但它對噪聲敏感。所以，算法在MLEM重建之后，先進行小波變換，然后在更穩定的小波域而不是噪聲圖像域進行基于絕對差分排序的各項異性擴散處理，減少噪聲對各項異性擴散的影響。實驗驗證表明：與其他常用算法相比，該算法重建出的圖像更干凈，含有更少的噪聲，信噪比更高，保持更多的圖像細節，重建效果更好。該算法可以應用于醫學CT領域中，能夠在降低輻射劑量的同時，有效地重建出符合要求的圖像。因此，該算法在醫學成像領域具有較好的應用前景。

參考文獻

[1] 張元科, 張軍英, 盧虹冰.低劑量CT圖像模型參數估計及統計去噪研究[J].西安電子科技大學學報,2011,38(3)：99-106.

[2] 張權，羅立民，桂志國.基于改進非局部先驗的Bayesian低劑量CT投影平滑算法[J].東南大學學報，2014，44(3)：499-503.

[3] Kachelriess M, Watzke O, Kalender W A. Generalized multi-dimensional adaptive filtering for conventional and spiral single-slice, multi-slice, and cone-beam CT[J]. Medical Physics,2001,28(4):475-490.

[4] 畢一鳴, 馬建華, 陳武凡.基于標準劑量CT圖像非局部權值先驗的低劑量圖像恢復[J].電子學報,2010,38(5):1146-1151.

[5] Gui Z G, Liu Y. Noise reduction for low-dose X-ray computed tomography with fuzzy filter[J].Optik-International Journal for Light and Electron Optics, 2012,123(13):1207-1211.

[6] 劉祎, 張權, 桂志國.基于模糊熵的低劑量CT投影降噪算法研究[J].電子與信息學報, 2013,35(6):1421-1427.

[7] Chen Y, Gao D Z, Nie C, et al. Bayesian statistical reconstruction for low-dose X-ray computed tomography using an adaptive-weighting local nonprior[J]. Computerized Medical Imaging and Graphics, 2009,33(7):495-500.

[8] 王麗艷, 韋志輝. 低劑量CT 的線性Bregman 迭代重建算法[J].電子與信息學報,2013,35(10):2418-2424.

[9] Rust G F, Aurich V, Reiser M. Noise dose reduction and image improvements in screening virtual colonoscopy with tube currents of 20 mAs with nonlinear Gaussian filter chains[C]//Medical Imaging 2002 Conference, New York: IEEE,2002:186-197.

[10] Lui D, Cameron A, Modhafar A, et al. Low-dose computed tomography via spatially adaptive Monte-Carlo reconstruction[J].Computerized Medical Imaging and Graphics, 2013,37(7-8):438-449.

[11] 王凱, 劉甲甲, 袁建英,等.基于小波子帶系數能量的優化權值降噪[J].計算機應用,2013,33(8):2341-2345.

[12] Zhong J, Sun H. Wavelet-based multiscale anisotropic diffusion with adaptive statistical analysis for image restoration[J].IEEE Transactions on Circuits and Systems,2008,55(9):2716-2725.

[13] 鐘瑩, 楊學志,唐益明,等.采用結構自適應塊匹配的非局部均值去噪算法[J].電子與信息學報,2013,35(12):2908-2915.

[14] Perona P, Malik J. Scale space and edge detection using anisotropic diffusion[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,1990,12(7):629-639.

[15] Chao S M, Tsai D M. An improved anisotropic diffusion model for detail and edge preserving smoothing[J].Pattern Recognition Letters,2010,31(13):2012-2023.

[16] Elbakri I A, Fessler J A. Statistical image reconstruction for polyenergetic X-ray computed tomography[J].IEEE Transactions on Medical Imaging,2002,21(2):89-99.

[17] Lu Hongbing, Li Xiang, Li Lihong, et al. Adaptive noise reduction toward low-dose computed tomography[C].SPIE Proceedings Medical Imaging, 2003: Physics of Medical Imaging,2003,5030:759-766.

[18] Li Tian-fang, Li Xiang, Wang Jing, et al. Nonlinear sonogram smoothing for low-dose X-ray CT[J].IEEE Transactions on Nuclear Science,2004,51(5):2505-2513.

[19] Garnett R, Huegerich T, Chui C, et al. A universal noise removal algorithm with an impulse detector[J].IEEE Transactions on Image Processing,2005 ,14(11):1747-1754.

[20] Liu J, Moulin P. Information-theoretic analysis of interscale and intrascale dependencies between image wavelet-coefficients[J].IEEE Trans Image Processing,2001,10(11):1647-1658.

[21] 王知強. 基于小波收縮與非線性擴散的去噪算法[J].計算機工程, 2011,37(7):249-252.

[22] Ling J, Bovik A C. Smoothing Low-SNR Molecular Images Via Anisotropic Median-Diffusion[J].IEEE Transactions on Medical Imaging,2002,21(4):377-384.

中圖分類號TP391

文獻標識碼A

DOI:10.3969/j.issn.1000-386x.2016.02.038

收稿日期：2014-08-07。國家自然科學基金項目(61071192,61271357,61171178)；山西省國際合作項目(2013081035)；山西省研究生優秀創新項目(2009011020-2)；山西省研究生優秀創新項目(20123098)；中北大學第十屆研究生科技基金項目(20131035)；山西省高等學校優秀青年學術帶頭人支持計劃項目；中北大學2013年校科學基金計劃。董嬋嬋，碩士生，主研領域：圖像降噪和圖像重建。桂志國，教授。張權，副教授。郝慧艷，副教授。張芳，碩士生。劉袆，博士。孫未雅，碩士生。