Institution框架下的結構化標記共變-逆變模擬

黃 振 華

(南京航空航天大學計算機科學與技術學院　江蘇 南京 210016)

?

Institution框架下的結構化標記共變-逆變模擬

黃 振 華

(南京航空航天大學計算機科學與技術學院江蘇 南京 210016)

摘要結構化標記共變-逆變模擬是共變-逆變模擬的一種擴充，在處理轉換系統的模擬關系時考慮了標記本身的結構。結構化標記模態轉換系統間的模態精化與結構化標記共變-逆變模擬之間存在諸多相似之處，為了在更抽象層次上研究兩者的關系，引入Institution框架。基于該框架，討論結構化標記模態轉換系統間的模態精化與結構化標記共變-逆變模擬之間的關系，并證明前者到后者存在Institution態射。結果表明，相比結構化標記模態轉換系統中模態精化關系，結構化標記共變-逆變模擬具有更強的表達能力。

關鍵詞Institution結構化標記模態轉換系統共變-逆變模擬

LABEL-STRUCTURED COVARIANT-CONTRAVARIANT SIMULATION IN INSTITUTION FRAMEWORK

Huang Zhenhua

(School of Computer Science and Technology,Nanjing University of Aeronautics and Astronautics,Nanjing 210016,Jiangsu,China)

AbstractThe label-structured covariant-contravariant simulation is an expansion of covariant-contravariant simulation,which considers the structure of labels themselves in dealing with the simulation relation of transition systems. There are many similarities between the modal refinement in label-structured modal transition systems and the label-structured covariant-contravariant simulation. In order to gain more insight into the relationship between them at a more abstract level,the Institutions framework is introduced. Based on that framework,we discuss the relationship between modal refinement in label-structured modal transition systems and label-structured covariant-contravariant simulation,and prove that there exists an Institution morphism from the former to the latter. This result indicate that label-structured covariant-contravariant simulation is more expressive than modal refinement relationship in label-structured modal transition systems.

KeywordsInstitutionLabel-structuredModal transition systemCovariant-contravariant simulation

0引言

在進程代數研究領域，轉換系統作為重要的語義模型應用廣泛，其中最常見的是帶標記的轉換系統LTS(Label Transition System)[1]，它可用于描述一般的并發系統的行為。模態轉換系統MTS(Modal Transition System)[2，3]本質上是一種LTS，其將轉換分成了兩種類型：可能轉換和必然轉換。實際上，一般的LTS也可以看作是可能轉換與必然轉換一致的MTS。不少的研究擴充了MTS概念，文獻[4]介紹了幾種定量模態轉換系統(Quantitative MTS)、時序模態轉換系統(Timing MTS)、加權模態轉換系統(Weighted MTS)和概率模態轉換系統(Probabilistic MTS)等。這些MTS的最大特點在于，轉化標記上附加了定量信息。最近，Bauer等人提出結構化標記模態轉換系統LSMTS(Label-Structured MTS)[5，6]，對帶有定量信息的MTS進行了一般性研究。

Fábregas等人提出了LTS之間的共變-逆變模擬[7，8]，其將動作集劃分為共變動作集、逆變動作集與互變動作集，并將模態邏輯語言 HML與動作的類型聯系在一起，建立了共變-逆變模擬的模態邏輯特征。采用共變-逆變模擬考查精化關系時，對于不同的動作集，在模擬關系中的處理方式也不一樣。基于共變-逆變模擬的LTS與基于模態精化的MTS之間存在諸多相似之處，Aceto等人對兩者之間的聯系做了討論[9，10]，并給出了它們之間的相互轉換關系。

然而，基于共變-逆變模擬的LTS并未考慮標記自身所帶有的結構，因此，本文引入了結構化標記轉換系統LSTS(Label- Structured Transition System)和結構化標記共變-逆變模擬LSCCS(Label-Structured Covariant-Contravariant Simulation)，并在Institution框架下討論了LSMTS與LSCCS之間的聯系。

1Institution與Institution態射

在計算機理論和數理邏輯的研究中，由于處理的問題不同，通常所采用的邏輯系統也不一樣。常見的邏輯系統包括一階邏輯、高階邏輯、Horn子句、類型論、等式邏輯、時序邏輯、模態邏輯和無窮邏輯等。目前尚且沒有哪一種邏輯系統適用于所有問題。然而，一個十分自然的問題是：能否建立一個一般性的框架，用來刻畫從一個邏輯系統到另一個邏輯系統的轉換，并描述各種邏輯系統之間的關系。基于這種考慮，Goguen和Burstall提出了Institution和Institution態射[10]。Institution為不同的形式系統提供了一個統一的組織方式，一階邏輯、等式邏輯、命題邏輯、三值一階邏輯和函數式程序邏輯等已經被證明是Institution[15]。

對于一個邏輯系統而言，其Institution包括四個基本組成部分：符號集、代數(或模型)、邏輯語句以及該模型和語句之間的滿足關系。與經典邏輯系統和模型論相比，Institution框架側重于考查由符號集的改變而帶來的影響。在建立軟件規范和設計軟件系統的過程中，有些情況下需要考慮從一個符號集轉變到另一個符號集，這一過程就是所謂的符號態射。典型的符號態射包括符號重命名、添加一些符號或將一些符號變為僅內部可見等，任何的符號態射均會引起模型和語句發生相應的變化。直觀上，語法(符號、語句)和語義(模型)的轉換方向是正好相反，不僅如此，兩者變化過程中還必須保持其滿足關系不發生改變，即：可滿足關系不隨符號的改變而發生改變，這是一個邏輯系統滿足Institution的重要條件。

下面將介紹Institution與Institution態射等基本概念，更詳盡的介紹可參考文獻[12-14]。本文假定讀者熟知范疇、函子和自然變換等范疇論基本概念。本文所采用的記號與Mac Lane所著的[16]相一致。在下文中，Set表示集合范疇，Cat表示范疇的范疇，|C|表示范疇C中對象的集合。

定義1[10]Institution是一個四元組(Sign,Sen,Mod,)，其中，Sign是一個范疇，其對象稱為符號集；Sen:Sign→Set是一個函子，將符號集Σ映射到一個Σ-語句集Sen(Σ)；Mod:Sign→Catop是一個函子，其將符號集Σ映射到Σ-模型與Σ-模型態射組成的范疇Mod(Σ)；表示集合{Σ|Σ∈|Sign|}，其中Σ?|Mod(Σ)|×Sen(Σ)，稱作Σ-滿足關系。對于Sign中任意態射f:Σ→Σ′，M′∈|Mod(Σ′)|和φ∈Sen(Σ)，如下條件成立：

M′Σ′Sen(f)(φ)?Mod(f)(M′)Σφ。

Institution僅能描述一個邏輯系統的基本要素，要刻畫從一個邏輯系統到另一個邏輯系統的轉換，就需要引入Institution之間的態射。從一個Institution到另一個Institution的態射有多種不同的定義方式，其中Institution態射和Institution余態射是最常見的兩種[2]。前者適用于從一個復雜的Institution映射到一個相對簡單的Institution，而后者通常與前者相反。本文僅涉及Institution態射。

定義2[11]給定Institution=(Sign,Sen,Mod,)和′=(Sign′,Sen′,Mod′,′)，從到′的Institution 態射包括三部分：函子Φ:Sign→Sign′、自然變換β:Mod?Mod′°Φ和自然變換α:Sen′°Φ?Sen。并且，對于任意Σ∈|Sign|、M∈|Mod(Σ)|和φ∈Sen′(Φ(Σ))，如下條件成立：

MΣαΣ(φ′)?βΣ(M)。

2LSMTS和LSCCS

本節首先介紹標記集及其相關性質，在此基礎上，介紹結構化標記模態轉換系統(LSMTS)及其模態精化，并給出了幾個例子。然后，將標記集運用到標記轉換系統中，引入結構化標記轉換系統，并將共變-逆變模擬[6]進行擴充，引入結構化標記共變-逆變模擬(LSCCS)。最后，給出了一個從LSMTS到LSCCS的轉換。

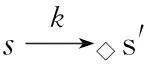
下文將使用圖來表示LSMTS，并約定虛線表示可能轉換，實線表示必然轉換，如果兩個狀態之間同時存在必然轉換和可能轉換且標記相同，則僅畫出必然轉換。下文中例1—例3均源自于文獻[5]。

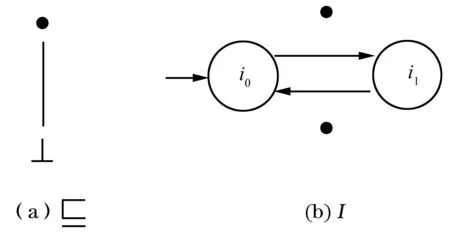
圖1　一個平凡的LSMTS

在經典的模態轉換系統中，模態精化過程就是去除一些可能轉換和(或)將一些可能轉換轉變為必然轉換的過程；而在LSMTS中，模態精化還需要考慮標記本身的精化關系。

圖2　自動售貨機LSMTS

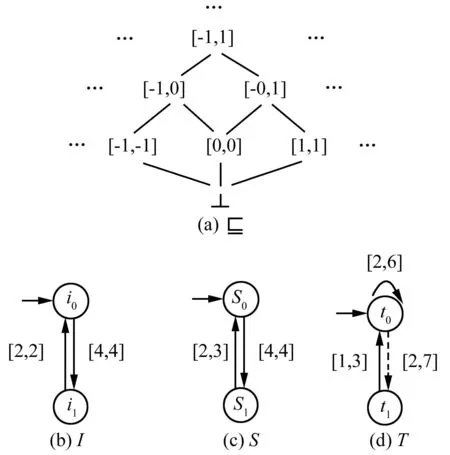
圖3　加權模態自動機

LTS可以看作是可能轉換與必然轉換一致的MTS，是進程代數研究中最重要的語義模型之一，可以描述并發系統的行為。下面回顧一下LTS中的共變-逆變模擬[5，6]。共變-逆變模擬將動作集劃分成三塊，即共變動作集、逆變動作集和互變動作集，對于不同的動作集，在模擬關系中的處理方式不一樣。

定義6[5]令P和Q是動作集A上的兩個LTS，初始狀態分別為p0和q0，{Ar,Al,Abi}是A上的一個劃分(其中Ar，Al，Abi允許為空集)。R?P×Q是P和Q之間的共變-逆變模擬關系當且僅當(p0,q0)∈R且對于任意的(p,q)∈R，如下條件成立：

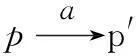
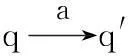
采用共變-逆變模擬考查精化關系時，規范中共變動作所標記的轉換必須在實現中被模擬；實現中逆變動作所標記的轉換必須在規范中被允許；而互變動作所標記的轉換必須滿足互模擬中的向前向后條件。本文將上述概念按如下方式推廣到LSTS上。

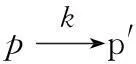
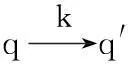
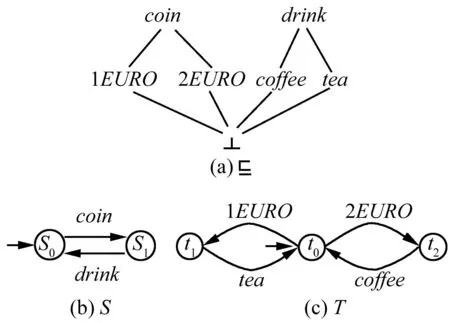
圖4　自動售貨機LSCCS

文獻[5]給出了基于模態精化的MTS與基于共變-逆變模擬的LTS之間的相互轉換關系，在這種轉換下，轉換之前與轉換之后的系統性質是保持的。與之類似，下面給出一個從LSMTS到LSCCS的轉換C。

{<⊥′,k>|k∈Kr∪Kl∪{⊥′}}。

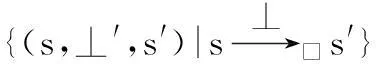
根據LSMTS和LSCCS的定義及如上的轉換C，有如下性質成立。

定理1R?P×Q是LSMTS P和Q之間的模態精化關系，當且僅當R-1是C(Q)和C(P)之間的結構化標記共變-逆變關系。

3Institution框架下的LSMTS和LSCCS

本節將在Institution框架下討論LSMTS與LSCCS之間的關系，并證明前者到后者存在Institution態射。

(1) f(K)=K′；

φ::=tt|ff|φ1∧φ2|φ1∨φ2|ψ|[k]ψ，其中k∈K{⊥}；

-Modmts(f)(M,m)與(M,m)的狀態集相同，且初始狀態相同；

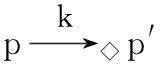
-Modmts(f)(H)=H。

證明容易驗證，Signmts是范疇，Modmts和Senmts是函子。所以，為證明mts是一個Institution，只需對Signmts中的態射f:(K,)→(K′,′)，(M′,s)∈|Modmts(K′,′)|和φ∈Senmts(K,)，證明如下條件成立即可：

按照公式φ的結構復雜度歸納證明，對于φ=tt、φ=ff、φ=φ1∧φ2和φ=φ1∧φ2這些情形，結論很容易證明，證明過程略。接下來考慮公式φ中含有模態詞的情形。

情形1φ=ψ。

(?)假設(M′,s)mtsSenmts(f)(ψ)，根據Senmts(f)的定義，(M′,s)mtsSenmts(f)(ψ)；由mts的定義可知，(M′,s)中存在，使得[l′]?[f(k)]且(M′,p)mtsSenmts(f)(ψ)；因為′具有完備性，所以，再根據函數f:K→K′滿足的條件可知，K中一定存在l使得f(l)=l′且lk，所以，(M′,s)中存在，使得lk且(M′,p)mtsSenmts(f)(ψ)；根據Modmts(f)的定義和的可靠性，由歸納假設可得，Modmts(f)(M′,s)中存在，使得[l]?[k]且Modmts(f)(M′,p)mtsψ；最后，根據mts的定義可得，Modmts(f)(M′,s)mtsψ。

(?) 假設Modmts(f)(M′,s)mtsψ，根據mts的定義，Modmts(f)(M′,s)中存在，使得[l]?[k]且Modmts(f)(M′,p)mtsψ；因為具有完備性，所以lk，根據函數f:K→K′滿足條件可知，f(l)′f(k)，因此[f(l)]?[f(k)]；根據Modmts(f)的定義，由歸納假設可得，(M′,s)中存在，使得[f(l)]?[f(k)]且(M′,p)mtsSenmts(f)(ψ)；根據mts的定義，(M′,s)mtsSenmts(f)(ψ)；最后，根據Senmts(f)的定義可得，(M′,s)mtsSenmts(f)(ψ)。

情形2φ=[k]ψ。

(?) 假設Modmts(f)(M′,s)mts[k]ψ；根據mts的定義，對于Modmts(f)(M′,s)中任意滿足[k]?[l]的，均有Modmts(f)(M′,p)mtsψ；因為具有完備性，所以kl，根據函數f:K→K′滿足條件可知，f(k)′f(l)，因此[f(k)]?[f(l)]；根據Modmts(f)的定義，由歸納假設可得，對于(M′,s)中任意滿足[f(k)]?[f(l)]的，均有(M′,p)mtsSenmts(f)(ψ)；根據mts的定義，(M′,s)mts[f(k)]Senmts(f)(ψ)；最后，根據Senmts(f)的定義可得，(M′,s)mtsSenmts(f)([k]ψ)。

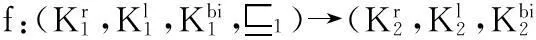
φ::=tt|ff|φ1∧φ2|φ1∨φ2|ψ|[k2]ψ，其中k1∈Kr∪Kbi，k2∈Kl∪Kbi。

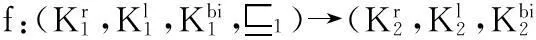
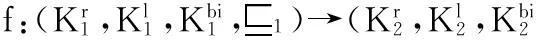
-Modcc(f)(M,m)與(M,m)的狀態集相同，且初始狀態相同；

-Modcc(f)(H)=H。

-對于k∈Kr∪Kbi，(M,s)ccψ?存在使得[l]?[k]且(M,s′)ccψ；

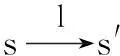
類似于LSMTS Institution，本文有如下結論成立。

定理2與定理3說明了定義9與定義10分別給出了LSMTS和LSCCS的Institution，下面將給出從mts到cc的Institution態射。

-Φ(f)(cv(k))=cv(f(k))；

-Φ(f)(ct(k))=ct(f(k))。

同樣，可按照公式φ的結構復雜度歸納證明，略。

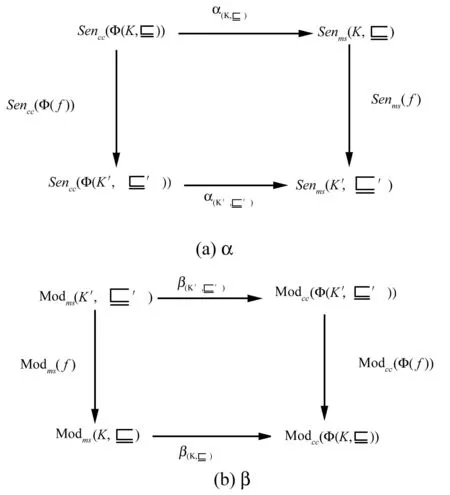
圖5　α和β的交換圖

4結語

本文引入了結構化標記模態轉換系統間的模態精化與結構化標記共變-逆變模擬，基于Institution框架，討論了兩者之間的聯系，并證明得出結構化標記模態轉換系統間的模態精化Institution到結構化標記共變-逆變模擬Institution存在Institution態射。結果表明，構化標記共變-逆變模擬具有更強的表達能力和更多應用場景，而結構化標記模態轉換系統間的模態精化具有更加直觀的特點，可以做為構化標記共變-逆變模擬的一種特例進行研究。本文從Institution 態射的角度研究了兩個系統的特點，然而，能否從Institution 余態射的角度來比較兩者之間的聯系，是一個值得進一步研究的問題。

參考文獻

[1] Keller R M. Formal verification of parallel programs[J]. Communications of the ACM,1976,19(7): 371-384.

[2] Larsen K G,Thomsen B. A modal process logic[C] //Logic in Computer Science,1988. LICS’88.,Proceedings of the Third Annual Symposium on. IEEE,1988: 203-210.

[3] Larsen K G. Modal specifications[C]//Automatic Verification Methods for Finite State Systems. Springer Berlin Heidelberg,1990: 232-246.

[4] Larsen K G,Legay A. Quantitative Modal Transition Systems[M]//Recent Trends in Algebraic Development Techniques. Springer Berlin Heidelberg,2013.

[5] Bauer S S,Juhl L,Larsen K G,et al. Extending modal transition systems with structured labels[J]. Mathematical Structures in Computer Science,2012,22(4): 581-617.

[6] Bauer S S,Fahrenberg U,Juhl L,et al. Weighted modal transition systems[J]. Formal Methods in System Design,2013,42(2): 193-220.

[7] Fábregas I,de Frutos Escrig D,Palomino M. Non-strongly stable orders also define interesting simulation relations[M]//Algebraand Coalgebra in Computer Science. Springer Berlin Heidelberg,2009: 221-235.

[8] Fábregas I,de Frutos Escrig D,Palomino M. Logics for contravariant simulations[M]//Formal Techniques for Distributed Systems. Springer Berlin Heidelberg,2010: 224-231.

[9] Aceto L,Fábregas I,de Frutos-Escrig D,et al. On the specification of modal systems: A comparison of three frameworks[J]. Science of Computer Programming,2013,78(12): 2468-2487.

[10] Aceto L,Fábregas I,de Frutos Escrig D,et al. Relating modal refinements,covariant-contravariant simulations and partial bisimulations[M] //Fundamentals of Software Engineering. Springer Berlin Heidelberg,2012: 268-283.

[12] Goguen J A,Burstall R M. Institutions: Abstract model theory for specification and programming[J]. Journal of the ACM (JACM),1992,39(1): 95-146.

[13] Goguen J,Ro?u G. Institution morphisms[J]. Formal Aspects of Computing,2002,13(3-5): 274-307.

[14] Diaconescu R. Institution-independent model theory[M]. Springer,2008.

[15] Sannella D,Tarlecki A.Foundations of algebraic specification and formal software development[M].Springer,2012.

[16] Mac Lane S.Categories for the working mathematician[M].Springer,1998.

[17] Milner R.Communication and concurrency[M].Prentice-Hall,Inc.,1989.

中圖分類號TP301.2

文獻標識碼A

DOI:10.3969/j.issn.1000-386x.2016.02.047

收稿日期：2014-09-05。國家自然科學基金項目(60973045)。黃振華，碩士生，主研領域：進程代數。