帶有停滯檢測的蟻群算法在2D HP格點模型中的應用

劉　羽　熊壬浩

1(桂林理工大學機械與控制工程學院　廣西 桂林 541004)

2(桂林理工大學信息科學與工程學院　廣西 桂林 541004)

?

帶有停滯檢測的蟻群算法在2D HP格點模型中的應用

劉羽1熊壬浩2

1(桂林理工大學機械與控制工程學院廣西 桂林 541004)

2(桂林理工大學信息科學與工程學院廣西 桂林 541004)

摘要為了提高蛋白質折疊結構預測的求解效率，針對2D HP格點模型，研究蟻群ACO(Ant Colony Optimization)算法在該問題上的應用。采用四元組表示絕對的折疊方向，并建立構象和解的一一對應關系。通過實驗對算法各階段的常用策略、方法進行比較分析。為了防止搜索陷入停滯，引入位置信息素停滯比和序列信息素停滯比兩個參數，使用一種新的停滯檢測機制。實驗結果表明，改進的算法在保證預測質量的前提下，顯著地提升了收斂速度。

關鍵詞HP模型蛋白質折疊蟻群算法停滯檢測遺傳算法

APPLICATION OF ANT COLONY OPTIMISATION ALGORITHM WITH STAGNATION DETECTION IN 2D HP LATTICE MODEL

Liu Yu1Xiong Renhao2

1(School of Mechanical and Control Engineering,Guilin University of Technology,Guilin 541004,Guangxi,China)2(School of Information Science and Engineering,Guilin University of Technology,Guilin 541004,Guangxi,China)

AbstractAiming at 2D HP lattice model we studied the application of ant colony optimisation algorithm on protein folding structure prediction in order to improve the efficiency of its solution. We used the quadruple to express absolute folding direction, and established the one-to-one correspondence between conformation and solution. Through experiment we made the comparative analyses on common strategies and methods in each stage of the algorithm. To prevent the search from going to stagnation, we introduced two parameters, the position pheromone stagnation ratio and the sequence pheromone stagnation ratio, and applied a new stagnation detection mechanism as well. Experimental results showed that the improved algorithm remarkably accelerated the convergence speed on the premise of ensuring prediction quality.

KeywordsHP modelProtein foldingAnt colony optimisationStagnation detectionGenetic algorithm

0引言

蛋白質是一種復雜的有機化合物，是由氨基酸經脫水縮合反應形成多肽鏈，然后在空間進行折疊后形成的。蛋白質是細胞的基本構成物質，是生命的物質基礎，在生物細胞中起著關鍵的生物和化學作用。蛋白質折疊問題的研究在醫學及生物工程等領域具有重大的科學價值和實用價值，其規律尚未被完全揭示。目前蛋白質折疊結構研究的主要方法包括實驗方法以及理論預測兩類。X射線晶體學方法等生物化學實驗方法對樣本的要求高、耗資大、周期長，人們逐漸將注意力轉移到理論預測方法上來。最新研究進展表明，一些小型蛋白質的精確折疊結構已使用計算機模擬得出[8]。如何從理論上建立相互作用模型是蛋白質折疊理論的核心問題。1989年Dill等提出的HP格點模型在內的簡化模型兼顧了折疊過程的物理機制以及計算機的計算能力，從而受到廣泛認可。

HP格點模型上的預測算法主要包括進化算法和蒙特卡羅算法兩類。基于蒙特卡羅算法的預測算法應用廣泛，但收斂速度較慢。2001年Liang等將遺傳算法引入蒙特卡羅算法，取得了一定效果。1996年Dorigo等提出了ACO算法，該算法成功應用于旅行商問題、車輛調度等問題。隨后Shmygelska[4,7]等將ACO算法應用于HP格點模型，取得了較好的效果。

目前已有較多文獻對HP格點模型上的ACO算法提出了進一步改進。例如，文獻[2]用PERM評價構型好壞的標準作為蟻群更新時的跡，同時采用EO算法進行局部搜索；文獻[5,7]分別在算法的局部搜索階段采用了牽引移動的方法和長距離移動的方法；文獻[3]提出了一種先用遺傳算法生成信息素分布，再利用蟻群算法求優化解的新的混合算法；文獻[4]引入了最大-最小蟻群系統中的信息素平滑機制等。這些改進涉及ACO算法的各個階段，效果不一，但少有文獻對相關的策略方法進行衡量，對算法停滯問題的研究也較少。對此，本文通過大量實驗比較分析ACO算法中常見的方法策略，在此基礎上使用一種新的停滯檢測機制，最后與其他ACO算法的效果進行比較。

12D HP格點模型

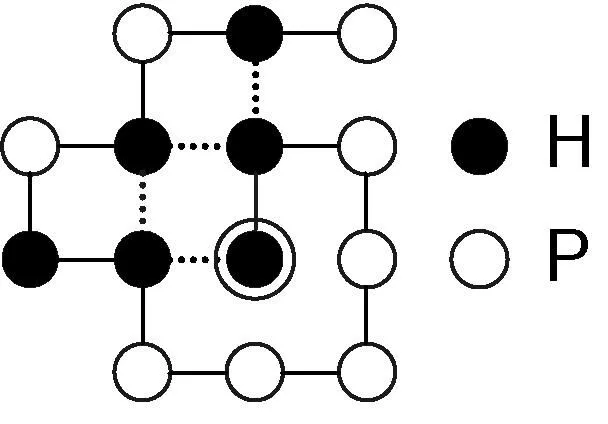
圖1　序列H2P5H2PHPHP的一個構象

HP格點模型(Hydrophobic-Polar Square Lattice Model)分為2D HP格點模型和3D HP格點模型，前者應用較為廣泛。本文僅針對2D HP格點模，但可擴展為3D HP格點模型。在2D HP格點模型中，氨基酸脫水縮合形成多肽鏈時被簡化為疏水性和親水性兩種，蛋白質則被表示為由疏水性殘基H和親水性殘基P組成的序列S。HP模型基于蛋白質折疊的熱力學假說，即天然構象的蛋白質處于熱力學最低的能量狀態。因此蛋白質折疊的過程被表示為序列S在二維網格上盤旋成能量最低的“構象”過程。網格上的一個格點只能被一個殘基占據。S中不相鄰，構象C中相鄰的H-H對稱為H-H鍵。C的能量用H-H鍵的數目n表示，表達式為EC= -1 × n。例如，圖1所示殘基序列H2P5H2PHPHP的構象，其自由能為-4。

2蟻群算法

2.1解的表示

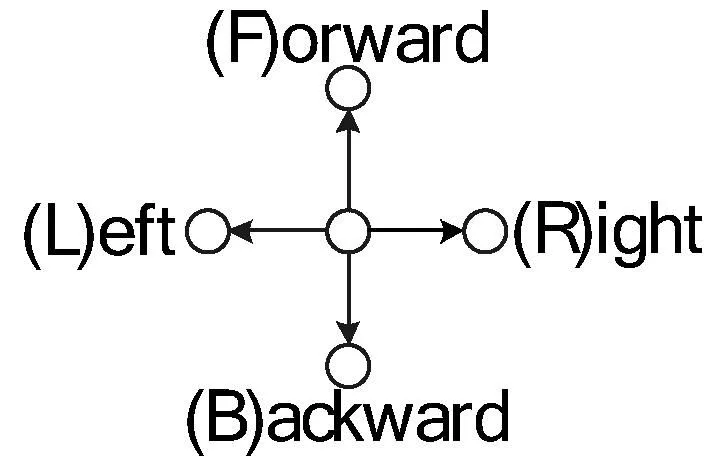
圖2　折疊方向的定義

HP模型中的殘基序列可表示為S=s1,s2,…,sn,si∈{H,P}。向網格中放置序列中的殘基si時，常用相對的方向[2-5,7]表示折疊過程，此時折疊方向序列可表示為D′=d1,d2,…,dm,di∈{S,L,R}，其中S、L、R分別代表直行、左轉和右轉。例如圖1中構象的方向序列為D′=RRSRSRLRRRRS。由于方向是相對的，必須至少固定兩個殘基的位置之后才能確定下個殘基的折疊方向，因此方向序列的長度為m=n-2。與此不同，實現采用了與文獻[1]所述相似的表示方式。如圖2所示，將方向序列定義為D=d1,d2,…,dm,di∈{F,B,L,R}，即用4個絕對的折疊方向F、B、L和R表示，此時方向序列的長度m=n-1。使用該定義圖1所示構象的方向序列為D=FRBBLLFLFRFRR。絕對的折疊方向更加直觀。

殘基序列S和方向序列D共同構成一個解。一個解只能表示一個構象，但一個構象可以用多個解表示。指定構象的起始殘基(圖1中用同心圓圈出)后，建立起解和構象的一一對應關系。考慮到構象在空間經旋轉、翻轉等操作(或以上操作的組合)后得到的構象實際上為同一構象，此時方向序列可能不唯一。通常2D HP模型不考慮構象的空間變換，但兩個不同的方向序列是否表示同一構象是可以判定的。

2.2建立構象

蟻群算法中，該階段每只螞蟻進行一次構象。構象的建立從隨機選定的位置si(1≤i≤n)開始，每增加一個殘基稱為“擴展”。從位置i向i+1進行擴展時稱為“正向”擴展，i向i-1稱為“反向”擴展。以正向擴展為例，從位置i以方向d進行擴展時，以概率Pi,d隨機選擇擴展方向，公式為：

(1)

信息素τi, d和啟發信息ηi, d共同決定擴展方向，其中d∈{F, B, L, R}，參數α和β分別反映了信息素和其發信息的重要程度。ηi,d的常見形式有以下兩種：

ηi,d=1+hi,d

(2)

(3)

其中，hi,d為從當前位置i以方向d擴展后增加的H-H鍵數目，T為取值[0.25, 0.35]的常數。下面將式(2)簡稱為HR1，式(3)簡稱為HR2。本文采用HR2，實驗部分對HR1、HR2兩組啟發函數進行了進一步討論。

構建過程中有可能出現網格上四個方向的鄰接格點都被占據而無法繼續擴展的情況，稱為“阻塞”。常見的處理策略有重新構造、回退、淘汰-克隆等策略。初步分析可知重新構造、回退策略耗時較多，但搜索到更多不同構象的可能性較大，而克隆策略耗時少同時易于實現。克隆策略淘汰無效的構象，并以概率Pi隨機從有效構象克隆。設有效構象共m個，從構象Ci克隆的概率為：

(4)

本文采用回退策略，實驗部分對回退、淘汰-克隆兩種策略進行了進一步討論。

2.3局部搜索

構象構建階段結束后，選擇一定比例具有較小能量的構象，對每個構象進行若干次局部搜索。較好的局部搜索方法包括“長距離移動”[7]、“牽引移動”[5,6]等。長距離移動是相對于“短距離移動”，例如“單點變異”和“多點變異”等來說的，它對于致密的構象依然有效，而牽引移動的優點是只需調整少數頂點即可達到有效構象。本文采用牽引移動方法，實驗部分對兩種方法進行了進一步討論。與殘基的擴展類似，牽引移動也有正向、反向兩個方向。仍以正向為例，隨機選擇殘基序列中的位置i，另設網格中的兩個格點e、f，位置i、i+1與e、f構成如圖3所示的矩形(不失正確性，假定i、i+1垂直排列)，其中i的對角為f。

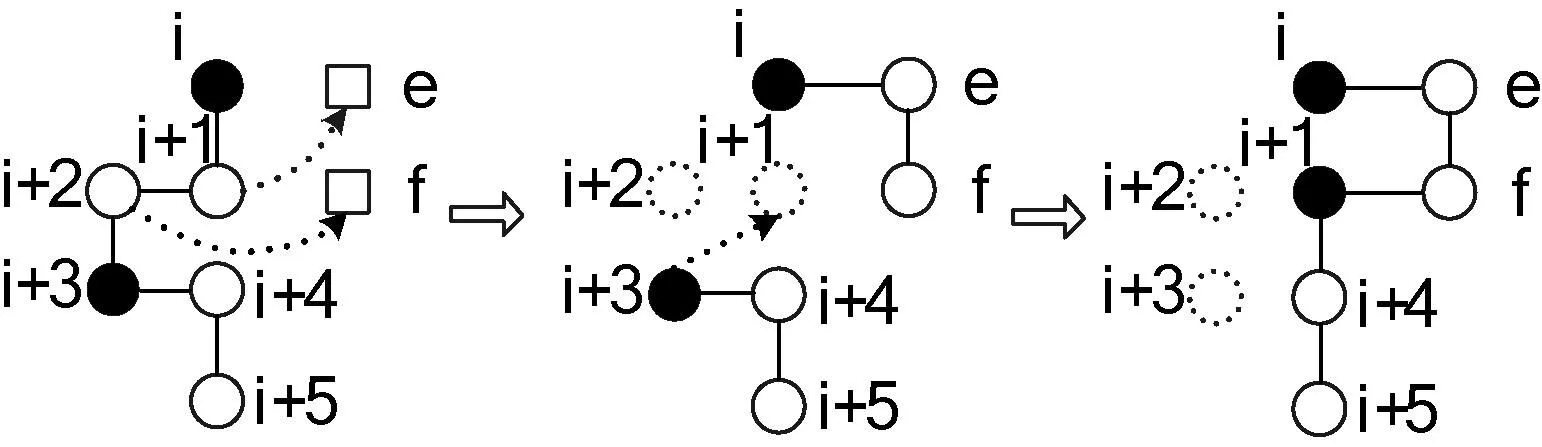
圖3　正向牽引移動示例

牽引移動算法描述如下：

Step1若e位置為空，且f為空或i+2，轉至Step2，否則移動失敗，退出算法；

Step2將i+1移動到e。如果e與i+2相鄰，轉至Step5，否則轉至Step3；

Step3將i+2移動的f。如果f與i+3相鄰，轉至Step5，否則轉至Step4；

Step4將j+3移動到原殘基j+1所在位置(i≤j≤n-3)，直至形成一個可行的構象，轉至Step5；

Step5若新構象具有更小的能量，移動成功，接受該構象，退出算法，否則移動失敗，退出算法。

以i、i+1為一條邊的矩形有兩個，對應的兩對e、f分別在邊i、i+1的兩側。為了加快收斂速度，牽引移動時使用了貪心策略，對兩對e、f先后進行搜索，取較優的結果。反向牽引移動類似，將圖3中i+1, i+2,…變為i-1, i-2,…可得到反向牽引移動的一個示例。文獻[6]證明了牽引移動并非完全可逆，本文采用了該文獻給出的修正版本。

2.4更新信息素

完成構象的構建和局部搜索后，信息素按下式衰減：

τi, d=ρτi, d

(5)

其中，ρ是信息素殘留比。然后選擇一定比例具有較小能量的構象進行信息素的增強：

τi, d=τi,d+ EC/Em

(6)

其中，Em是序列已知的最小能量值。初始狀態下τi,d= 0.25，隨著迭代的進行，某些方向上的信息素不斷增加，如果這些方向上的信息素遠大于其他方向上的信息素，造成選擇其他方向的概率非常低，搜索將會陷入停滯狀態。為了防止搜索陷入停滯狀態，常用類似于最大-最小蟻群系統中的方法對信息素進行調整[4](下面簡稱為MM)。每次更新信息素后，首先將τi,d標準化，使得∑d∈{F,B,L,R}τi,d=1。設τi, max和τi, min分別為τi, d中最大和最小的信息素，如果τi, min<θ，則令τi, max= τi, max- (θ - τi, min), τi, min=θ。

2.5帶有停滯檢測的蟻群系統(SD-ACO)

MM在每次更新信息素后進行，可以避免系統陷入停滯狀態。MM的缺陷在于，它無法確定對信息素進行調整的時機，具有一定的盲目性。分別針對各個位置i對τi,d進行調整，全局性較差。同時，由于信息素的積累與構象的方向選擇是一種正反饋機制，過早的調整信息素必然對收斂速度有所影響。若能通過某種方式對停滯做出檢測，將能很好地解決上述問題。為此，引入位置信息素停滯比ε和序列信息素停滯比μ(0.5<ε<1，0<μ<1)兩個參數，并定義：

(7)

(8)

通過對大量實驗數據的統計分析，發現使用G能夠很好表示停滯。使用上述ACO算法進行搜索(參數設置參考實驗部分)，正常更新信息素，但不進行調整。迭代若干次，統計每次迭代后G的值以及問題的求解比(當前最優能量/Em，見圖4中圖例Solve)，所有迭代完成后取平均。圖4給出了實驗部分所述序列Ser10的統計結果，其中ε分別取四個不同的值，橫軸為迭代次數，縱軸為G值或求解比。可見求解比和G值均在一定次數的迭代后趨于穩定。實驗中發現，G趨于穩定后，特定方向上的τi,d持續增大，選擇其他方向的可能性減小，而且這種情況隨著搜索的繼續越來越嚴重，以至搜索陷入停滯。對其他序列的實驗結果也得出相似的特征，這就為文中所述停滯檢測方法提供了可行性驗證，也為ε和μ兩個參數的設置提供了依據。停滯檢測的具體方法為，若G>μ則認為搜索已經停滯，隨后放棄整個蟻群系統，對τi,d進行重置。本文將這種機制稱為SD(Stagnation Detection)，將使用這種機制的蟻群系統稱為SD-ACO。

圖4　迭代次數與求解比、G值的關系

SD基于對τi,d的統計分析，相對于MM，SD先進行停滯檢測，再進行進一步處理。它使用了更全面的信息，即所有位置i上τi,d的整體狀況作為判斷依據，能夠更好地反映信息素的全局狀況。SD-ACO借鑒了遺傳算法的淘汰機制，對陷入停滯的蟻群系統進行淘汰，并用新的系統取而代之。實踐證明，SD-ACO更充分地利用了蟻群系統的構象能力，保證了解的質量，同時具有更快的收斂速度。SD還可與其他機制結合，例如與MM結合。即將SD用作單純的檢測機制，同時將MM作為平滑機制。用SD檢測到停滯后不重置τi,d，而是按照MM的方式進行調整。文中將這種混合機制稱為SD-MM。實驗部分對MM、SD和SD-MM進行了比較。

3實驗結果及分析

本文幾組實驗對蟻群算法相關步驟中的一些策略、方法進行了分析，最后比較了帶有停滯檢測的蟻群算法以及若干其他改進的ACO算法。算法使用C語言實現，編譯器為pgcpp 13.6-0，運行環境配置有Intel Core i5 @ 3.2 GHz處理器，操作系統為CentOS。為了更全面地評估算法的性能，實驗使用了文獻[1]給出的15組基準序列，并將其編號為Ser1到Ser15。如無特別說明，實驗參數設置均設置為α=1,β=2,ρ=0.8。螞蟻數均為200只，用于局部搜索和信息素更新的比例為1%，局部搜索次數500次，迭代次數為10 000次。實驗結果中的時間均為CPU時間，單位秒。

3.1HR1與HR2的比較

下面對啟發函數HR1和HR2進行實驗比較。構象調整的效果依賴于起始構象的能量，較差的起始構象很少能被調整為高質量的解[4]。啟發函數對構象的建立有重要的指導作用，較好的構象為局部搜索調整出高質量的解提供了更大的可能性。實驗僅關注HR1、HR2的啟發能力，即啟發函數對構象能量的影響，構象構造完成后不進行局部搜索，也不對信息素進行更新。不限制迭代次數，將運行時間限制在1800 s內，HR2中T取0.25。對于長度不大于36的短序列Ser1-8，分別獨立運行100次，對于長序列Ser9-15運行20次。圖5給出了Ser10-15的結果，縱軸為平均時間，百分比為達到能量的概率，“+”號后為得到的能量與Em的差值。

圖5　Ser9-Ser15兩組啟發函數的比較

對于短序列，兩者均能以100%的概率得到最優解，但HR2所用時間遠小于HR1。對于長序列，HR2搜索到的解優于HR1，且時間性能較好。此外，對于短序列，僅使用隨機搜索即可在較短時間內得到最優解。對于長序列，隨機搜索的求解能力不足，且容易“早熟”。如對于Ser12-15，使用HR2分別早在485、648、1101和945 s已找到最終解。綜上，HR2的啟發能力明顯優于HR1。后續實驗中均使用HR2。

3.2阻塞處理與局部搜索

下面對回退、淘汰-克隆兩種處理策略和長距離移動、牽引移動兩種局部搜索方法進行實驗比較。阻塞處理影響算法的收斂速度及解的質量，與局部搜索密切相關。因此實驗對上述策略、方法的四種組合，即RB-LRM、RB-PM、CLN-LRM、CLN-PM分別進行了測試。局部搜索后不進行信息素的更新，達到迭代次數后停止，各序列分別使用四種組合各自獨立運行100次。RB中回退長度為已折疊序列長度的一半(向下取整)，CLN中選擇%1的有效構象，LRM中選擇與上個殘基相同方向的概率為0.5。LRM與PM均使用了貪心策略，每次局部搜索選擇正向、反向搜索中較優的構象。為節約篇幅，表1和表2僅給出了Ser12-15的部分運行結果，即100次運行達到相應能量(E)的概率(P)、平均時間(T)及平均迭代次數(R)。空行表示沒有達到相應能量。

表1　RB-LRM與RB-PM的結果比較

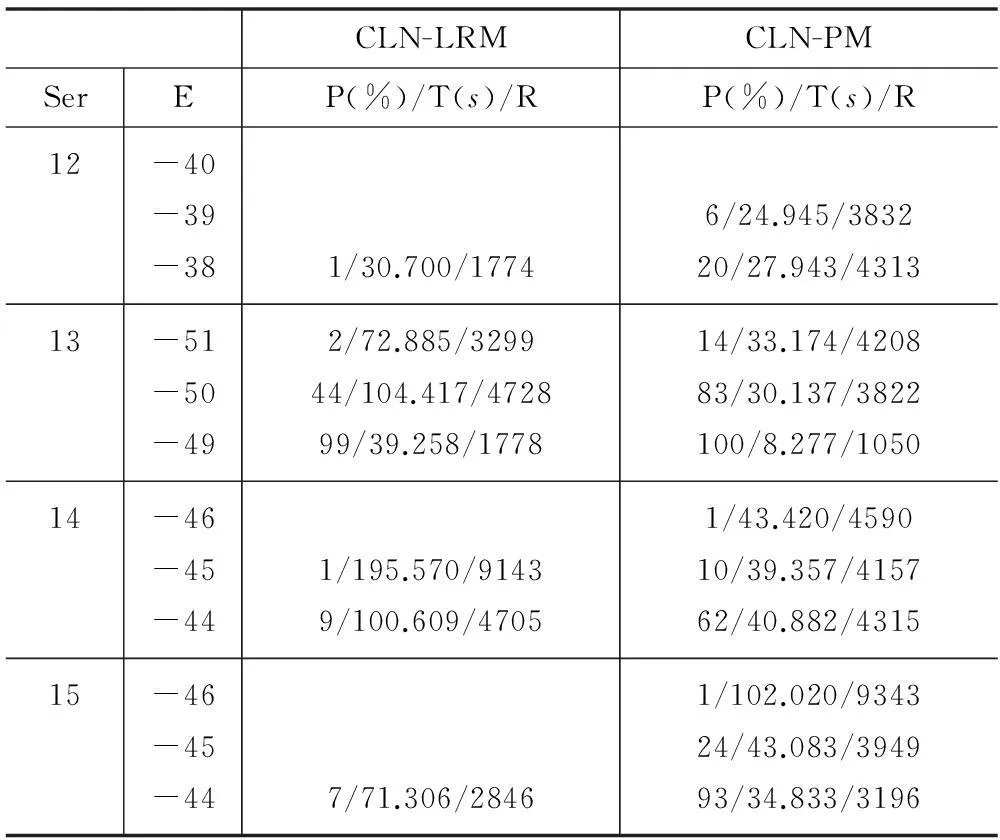
表2　CLN-LRM與CLN-PM的結果比較

將表中數據RB-LRM與RB-PM相比、CLN-LRM與CLN-PM相比，PM的最終解更好，E相同時PM的收斂速度更快、概率更大。將RB-LRM與CLN-LRM相比、RB-PM與CLN-PM相比，E相同時RB的概率更大，但收斂速度慢于CLN。Ser14中CLN-PM的最終解好于RB-PM，但CLN-PM僅以1%的概率得到該解，其他情況下RB的解均較優。Ser1-11的運行結果相似。綜上，局部搜索方法采用PM，為了保證解的質量，阻塞處理策略采用RB。后續實驗中均采用RB-PM。

3.3MM、SD以及SD-MM的比較

除默認參數外，其他參數θ=0.05，ε=0.75，μ=0.5。對于Ser1-13分別獨立運行100次，Ser14-15運行50次。表3僅給出了Ser12-15的部分運行結果，SD-ACO的結果可參見表4所示。其中“*”號標記的能量等于序列已知的最小能量(下同)。

表3　三種停滯處理機制的比較

易見無論是解的質量還是收斂速度SD、SD-MM均優于MM。Ser13中SD-MM的收斂速度遠快于SD，但求得最優解及次優解的概率均較低。Ser1-15中，僅對于Ser14，SD-MM的最終解概率高于SD，其他無論在求解質量還是收斂速度上，SD具有明顯優勢。

3.4SD-ACO與其他ACO算法的比較

SD-ACO的最終版使用HR2及RB-PM，對Ser1-13分別獨立運行100次，Ser14-15運行50次。表4給出了Ser1-15的測試結果，同時列出了其他文獻報告的結果。除文獻中已給出其改進ACO算法的命名外，其他均使用作者姓名首字母命名。表中數據第一行為能量值，“*”號標記的能量等于序列已知的最低能量(下同)，第二行為時間，空白行表示文獻未給出，若得到解的概率不為1，還給出了求得相應解的概率。

表4　SD-ACO與其他ACO算法的比較

對于Ser1-13，SD-ACO能夠保證解的質量，且收斂速度較快。對于Ser14-15，SD-ACO的解質量優于HSZ-ACO和HA，且收斂速度較快。總的來說SD-ACO的效果明顯，但Ser14中SD-ACO的解劣于LYPS-ACO，Ser15中SD-ACO的解劣于ACO-HPPFP-3。兩者均為運行較長時間后得到的，為進一步研究運行時間對SD-ACO解質量的影響，進行下述實驗。取消迭代次數限制，增加運行時間并觀察實驗結果。表4中，ACO-HPPFP-3以外其他算法列出的運行時間均在7000 s內，除Ser15外SD-ACO均達到了ACO-HPPFP-3所得的最優能量。為驗證同等時間條件下SD-ACO的效果，將時限設置為7200 s。此外，為比較不同時限下SD-ACO的運行結果，從而進一步分析運行時間對算法效果的影響，還使用時限3600 s進行了測試。對Ser12-15分別獨立運行20次，實驗結果如表5所示。

表5　兩組時限的測試結果比較

其中Ser12以100%的概率達到最優解，平均時間穩定在90 s內。雖然Ser14在時限3600 s時未找到解-47，但在時限7200 s時找到該解，且概率明顯增大。兩個時限下Ser13的兩組解均優于表4中的其他算法，Ser15求得-48的概率有較大提升。考慮到實際應用，沒有使用更大的時限進行測試，但從表5的結果可得出，隨著運行時間的增加，達到相應解的概率增大，且有可能得到質量更好的解。

4結語

HP格點模型是學術界廣泛接受的蛋白質折疊結構預測模型，將ACO算法應用于2D HP格點模型取得了較好的效果。眾多文獻對此提出了進一步改進，但效果不一。為衡量常見策略方法的優劣，本文比較分析了兩組啟發式函數、四對阻塞處理與局部搜索策略方法，并在此基礎上使用了一種新的停滯檢測機制SD，并進行實驗驗證，對蟻群算法作出了進一步改進。SD使用全局信息，通過參數化的方式檢測停滯，并借鑒遺傳算法的淘汰機制進行調整。與最大-最小蟻群系統中的停滯預防機制相比，SD不盲目調整信息素，檢測停滯的時機更為精準。實驗結果表明，將SD-ACO應用于2D HP模型取得了較好的效果。此外，并行化是提升算法效率的重要手段，這也是后續的研究方向。

參考文獻

[1] Mario GarzaFabre,Eduardo RodriguezTello,Gregorio ToscanoPulido.Comparative Analysis of Different Evaluation Functions for Protein Structure Prediction Under the HP Model[J].Journal of Computer Science and Technology,2013,28(5):870-873.

[2] 陸恒云,楊根科,潘常春,等.改進的蟻群算法求解蛋白質折疊問題[J].計算機工程與設計,2010,31(8):1787-1788.

[3] 李晚霞,莫忠息,曾濤.混合遺傳算法和蟻群算法在HP模型中的應用[J].計算機工程與應用,2006,42(31):58-59.

[4] Alena Shmygelska,Holger H Hoos.An ant colony optimisation algorithm for the 2D and 3D hydrophobic polar protein folding problem[J].BMC Bioinformatics,2005,6(30):18-21.

[5] 何蓮蓮,石峰,周懷北.改進的蟻群算法在2D HP模型中的應用[J].武漢大學學報:理學版,2005,51(1):35-37.

[6] Gy?rffy D,Závodszky P,Szilágyi A. ”Pull Moves” for Rectangular Lattice Polymer Models Are Not Fully Reversible[J].IEEE/ACM Transactions on Computational Biology and Bioinformatics,2012,9(6):1847-1848.

[7] Alena Shmygelska,Holger H Hoos.An Improved Ant Colony Optimisation Algorithm for the 2D HP Protein Folding Problem[C]//Lecture Notes in Computer Science,2003,2671:405-417.

[8] Ken A Dill,Justin L MacCallum.The Protein-Folding Problem,50 Years On[J].Science,2012,338(6110):1042-1045.

中圖分類號TP18TP301.6

文獻標識碼A

DOI:10.3969/j.issn.1000-386x.2016.02.053

收稿日期：2014-10-21。國家自然科學基金項目(41264005)；廣西教育廳科研項目(201102ZD018)。劉羽，教授，主研領域：并行計算，數據挖掘。熊壬浩，碩士。