基于MIC的MRG32k3a并行化設(shè)計(jì)與實(shí)現(xiàn)
宋博文 周津羽 華 誠(chéng) 劉 逍, 周曉輝,
1(西安郵電大學(xué)計(jì)算機(jī)學(xué)院 陜西 西安 710121)
2(陜西省高性能計(jì)算研究中心 陜西 西安 710121)
?
基于MIC的MRG32k3a并行化設(shè)計(jì)與實(shí)現(xiàn)
宋博文1周津羽2華誠(chéng)2劉逍1,2周曉輝1,2
1(西安郵電大學(xué)計(jì)算機(jī)學(xué)院陜西 西安 710121)
2(陜西省高性能計(jì)算研究中心陜西 西安 710121)
摘要隨機(jī)數(shù)產(chǎn)生器在工程模擬等領(lǐng)域獲得廣泛應(yīng)用,MRG32k3a是一種性能優(yōu)異的隨機(jī)數(shù)產(chǎn)生器,但產(chǎn)生速率較慢。針對(duì)這種情況,在研究MRG32k3a串行算法的基礎(chǔ)上,利用算法并行化理論,提出一種基于MIC(Many Integrated Core)平臺(tái)的MRG32k3a并行化方法。實(shí)驗(yàn)結(jié)果表明,該方法能通過(guò)TestU01的全部測(cè)試,移植到MIC平臺(tái)后加速比與線程數(shù)呈線性增長(zhǎng)關(guān)系,相對(duì)CPU單線程的最佳加速比為17.73。
關(guān)鍵詞隨機(jī)數(shù)產(chǎn)生器MIC并行化MRG32k3aTestU01
DESIGN AND IMPLEMENTATION OF MRG32K3A PARALLELISATION BASED ON MIC
Song Bowen1Zhou Jinyu2Hua Cheng2Liu Xiao1,2Zhou Xiaohui1,2
1(School of Computer Science and Technology,Xi’an University of Posts and Telecommunications,Xi’an 710121,Shaanxi,China)2(Shaanxi Research Center for High Performance Computing,Xi’an 710121,Shaanxi,China)
AbstractRandom number generator is widely used in engineering simulation, MRG32k3a is a random number generator with excellent performance, but its generation rate is slow. In view of this, this article presents an MIC platform-based MRG32k3a parallelisation approach using the theory of algorithm parallelisation according to the study on MRG32k3a serial algorithm. Experimental results show that the approach can pass all the tests of uniform random number test-library TestU01. After transplanting to MIC platform, the relationship of the speedup ratio and the number of threads increases linearly, and the best speedup ratio relative to CPU single-thread reaches 17.73.
KeywordsRandom number generatorMany integrated core (MIC)ParallelisationMRG32k3aTestU01
0引言
隨機(jī)數(shù)產(chǎn)生器是用來(lái)產(chǎn)生隨機(jī)數(shù)的裝置[1],一般分為真隨機(jī)數(shù)產(chǎn)生器和偽隨機(jī)數(shù)產(chǎn)生器。真隨機(jī)數(shù)通過(guò)物理實(shí)驗(yàn)或自然噪音等方式產(chǎn)生,成本高;偽隨機(jī)數(shù)通過(guò)若干種子利用數(shù)學(xué)算法遞推產(chǎn)生周期性的隨機(jī)數(shù)序列,不需要外部物理硬件的支持,并且具有類似于真隨機(jī)數(shù)的統(tǒng)計(jì)特征;因此,在科學(xué)研究和工程模擬領(lǐng)域主要應(yīng)用偽隨機(jī)數(shù)產(chǎn)生器。相對(duì)于現(xiàn)在普遍應(yīng)用的偽隨機(jī)數(shù)產(chǎn)生器LCG(Linear Congruential Generator)[2],MRG32k3a[3-5]具有長(zhǎng)周期、隨機(jī)數(shù)序列質(zhì)量?jī)?yōu)異的特點(diǎn),但較慢地產(chǎn)生速率制約了它的應(yīng)用。
隨著計(jì)算機(jī)系統(tǒng)結(jié)構(gòu)和計(jì)算機(jī)網(wǎng)絡(luò)技術(shù)的快速發(fā)展,科學(xué)研究和工程模擬對(duì)隨機(jī)數(shù)產(chǎn)生器的性能及速率要求也日益增長(zhǎng),研究隨機(jī)數(shù)產(chǎn)生器并行化是迫切的、必然的。并行計(jì)算技術(shù)迅速發(fā)展[6],將其應(yīng)用于隨機(jī)數(shù)產(chǎn)生器,成為提高隨機(jī)數(shù)產(chǎn)生器產(chǎn)生效率的方法之一。目前國(guó)內(nèi)外已經(jīng)做了一些隨機(jī)數(shù)產(chǎn)生器的并行技術(shù)的研究,并行方法總體分為兩種,第一種是每個(gè)線程獨(dú)自應(yīng)用不同類別的隨機(jī)數(shù)產(chǎn)生器,第二種是將一個(gè)隨機(jī)數(shù)產(chǎn)生器并行化到每一個(gè)線程中。第一種方法易于并行化,2000年Michael Mascagni等研發(fā)出了基于第一種方法的并行化隨機(jī)數(shù)產(chǎn)生器庫(kù)SPRNG(Scalable Parallel Random Number Generators Library),每個(gè)線程所使用的產(chǎn)生器都不相同[7];后來(lái)Shuang Gao等在此基礎(chǔ)上研發(fā)出基于統(tǒng)一計(jì)算設(shè)備架構(gòu)CUDA(Compute Unified Device Architecture)平臺(tái)的并行化隨機(jī)數(shù)產(chǎn)生器庫(kù)GASPRNG(GPU accelerated scalable parallel random number generator library)[8];Kinga Marton等于2011年提出的一種并行化隨機(jī)數(shù)產(chǎn)生器,各線程混合使用了不同類型的隨機(jī)數(shù)產(chǎn)生器[9]。第二種并行化方法則較難實(shí)現(xiàn),優(yōu)點(diǎn)是能保持隨機(jī)數(shù)產(chǎn)生器的原始序列。 2011年,Thomas Bradley等將第二種并行化方法總結(jié)為Simple skip ahead、Strided skip ahead和Hybrid三類,并且描述了基于GPU的MRG32k3a、Sobol和MT19937三種隨機(jī)數(shù)產(chǎn)生器的并行化算法及性能分析[10]。L’Ecuyer等人2001年也早以概述了MRG類隨機(jī)數(shù)產(chǎn)生器的并行化的理論過(guò)程,但沒(méi)有驗(yàn)證并行化后的結(jié)果正確性和運(yùn)行效果[11]。
目前隨機(jī)數(shù)產(chǎn)生器的并行化研究工作主要集中于多核中央處理器CPU平臺(tái),缺少基于Intel最新產(chǎn)品MIC平臺(tái)[12]并行化的相關(guān)理論依據(jù)和性能分析。另外,以上文獻(xiàn)均沒(méi)有詳細(xì)闡述MRG32k3a并行化的具體使用方法、并行化實(shí)施方案及并行化結(jié)果分析。本文利用“分而治之”思想實(shí)現(xiàn)MRG32k3a并行化,設(shè)計(jì)了一種簡(jiǎn)單的并行化規(guī)則,并確定了相應(yīng)的參數(shù),實(shí)現(xiàn)了按周期“分而治之”并行產(chǎn)生隨機(jī)數(shù)的算法,更主要的工作是基于MIC進(jìn)行了MRG32k3a并行化后的性能測(cè)試分析,檢驗(yàn)其可行性和優(yōu)越性。文獻(xiàn)[10]中Thomas Bradley總結(jié)的Simple skip ahead方法實(shí)質(zhì)上就是 “分而治之”思想在隨機(jī)數(shù)產(chǎn)生器應(yīng)用上的體現(xiàn),在一個(gè)周期內(nèi)劃分線程和分配任務(wù),每個(gè)線程獨(dú)立產(chǎn)生一段周期內(nèi)的連續(xù)的隨機(jī)數(shù)子序列。
本文主要研究工作分為以下三個(gè)階段:1) 理論研究MRG32k3a的串行與并行算法,確定最有效的并行化方案,進(jìn)行理論加速比和可擴(kuò)展性分析;2) 在Intel Xeon E5-2680上進(jìn)行了MRG32k3a串行和并行的大量開(kāi)發(fā)與測(cè)試,其中選用最為完備的均勻隨機(jī)數(shù)產(chǎn)生器測(cè)試庫(kù)TestU01進(jìn)行隨機(jī)數(shù)序列性能測(cè)試[13,14],借助TestU01檢測(cè)保證了并行化過(guò)程的正確性,最終MRG32k3a串行及并行算法均能完全通過(guò)TestU01 測(cè)試,同時(shí)完成相應(yīng)時(shí)間測(cè)試和加速比分析;3) 移植到MIC平臺(tái),通過(guò)測(cè)試挑選出最優(yōu)的Intel編譯選項(xiàng),然后完成時(shí)間測(cè)試和性能分析。實(shí)驗(yàn)數(shù)據(jù)顯示MRG32k3a并行化后的加速比和并行效率理想,MIC相對(duì)CPU單線程的最佳加速比為17.73。
1MRG32k3a串行算法及并行化方法
1.1MRG32k3a串行算法
組合多重遞歸隨機(jī)數(shù)產(chǎn)生器[3,4]CMRG( Combined Multiple Recursive Generator)遞推公式為:
xj,n=(aj,1xj,n-1+ … + aj,kxj,n - k)modmj
(1)

為兼顧速度和長(zhǎng)周期性,j= 2、k= 3時(shí)比較理想[5]。MRG32k3a屬于此種類型的CMRG,遞推公式為:
(2)
其中n≥3,a1,2=1 403 580,a1,3=-810 728,a2,1=527 612,a2,3=-1 370 589,m1=232-209,m2=232-22 853。
產(chǎn)生[0,1)之間的均勻隨機(jī)數(shù)un。
zn= (x1,n+ x2,n)modm1
(3)
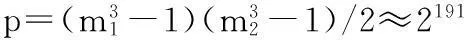
1.2MRG32k3a并行化算法設(shè)計(jì)
MRG32k3a產(chǎn)生的隨機(jī)數(shù)序列之間存在相互依賴關(guān)系,最大維度只有45[11],采用分治法可以避免維度約束。每個(gè)線程跳到隨機(jī)數(shù)序列特定位置后連續(xù)產(chǎn)生隨機(jī)數(shù),意思是說(shuō)把原始隨機(jī)數(shù)序列分割為V段,每個(gè)子序列都是原始序列的連續(xù)子序列,這些特定位置是每個(gè)線程初始值。本文將闡述MRG32k3a利用分治法并行化的具體實(shí)現(xiàn)過(guò)程。
設(shè)隨機(jī)數(shù)序列每個(gè)狀態(tài)為向量對(duì)形式:
Xi,n=(xi,nxi,n +1xi,n + 2)T
MRG32k3a遞推公式則轉(zhuǎn)化為:
Xi,n +1=AiXi,nmodmii=1,2
(4)
狀態(tài)向量組Xi,n+w可以直接由Xi,n計(jì)算:
(5)
令p是MRG32k3a的周期,T為轉(zhuǎn)換函數(shù),則T(Xn)=Xn+1,T(Xp)=X。整個(gè)周期的隨機(jī)數(shù)序列劃分成V=2v個(gè)長(zhǎng)度為W=2w的隨機(jī)數(shù)子序列,其中v+w=191。X0是隨機(jī)數(shù)序列的初始狀態(tài),每個(gè)隨機(jī)數(shù)子序列的初始狀態(tài)定義為:
C1=X0,C2=Tw(X0),…,Cg=Tw(Xg-1)=T(g-1)w(X0)
本文選取w=127,v=64,即最多運(yùn)行V=264個(gè)線程,各線程最多產(chǎn)生W=2127個(gè)隨機(jī)數(shù)序列,圖1為相應(yīng)的并行化原理圖。
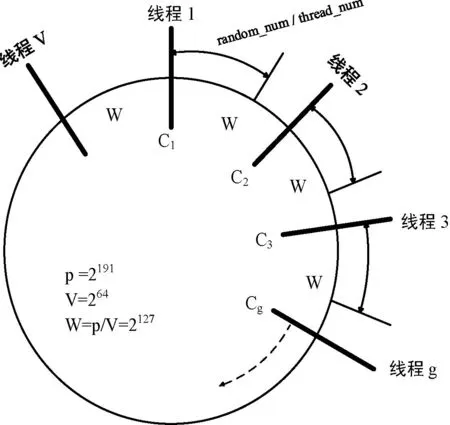
圖1 MRG32k3a并行化原理圖
如圖1所示,MRG32k3a并行化的關(guān)鍵點(diǎn)是計(jì)算每個(gè)線程的初始狀態(tài)Cg。其中,三個(gè)參量乘積的模運(yùn)算[1]定義為:
X·Y·Zmodm=((X·Ymodm)·Z)modm
(6)

MRG32k3a并行化的具體算法描述如算法1:
算法1MRG32k3a并行化算法
輸入: 種子seed[6],線程數(shù)thread_num,任務(wù)量random_num
輸出: random_num個(gè)隨機(jī)數(shù)u
Begin
(1) for i = 0 to thread_num do
(1.1) for j = 0 to 6 do
C[i][j] = seed[j]
end for
end for
(2) for all id where 0≤id≤thread_num do
(2.1) for j = 0 to random_num/thread_num do
p1 = a12 * C[id][1] - a13 * C[id][0]
p2 = a21 * C[id][5] - a23 * C[id][3]
u = ((p1 > p2) ?
(p1 -p2)/m1 : (p1 -p2 + m1)/m1
end for
end for
End
MRG32k3a串行算法產(chǎn)生n個(gè)隨機(jī)數(shù)序列,所需時(shí)間與n大小成正比,因此時(shí)間復(fù)雜度為O(n)或線性時(shí)間,它的并行算法在g個(gè)線程情況下時(shí)間復(fù)雜度為O(n/g),所以其絕對(duì)加速比為O(g),有效利用了線程數(shù)量,加速比隨著線程數(shù)增加而線性增長(zhǎng)。MRG32k3a串行算法的任務(wù)量與產(chǎn)生的隨機(jī)數(shù)總量random_num成正比,同時(shí)MRG32k3a的并行算法是將總?cè)蝿?wù)量平均分配給g個(gè)線程,理想情況下,并行算法的加速比接近于線程數(shù)。而當(dāng)任務(wù)量較少時(shí),一定的通信開(kāi)銷會(huì)額外消耗時(shí)間,比如分配線程、訪問(wèn)共享變量、內(nèi)存間轉(zhuǎn)換等操作,相應(yīng)的加速比會(huì)下降,而任務(wù)量逐漸增加后,通信開(kāi)銷所占比例越來(lái)越小,逐漸呈現(xiàn)出線性加速。

1.3基于MIC并行算法實(shí)現(xiàn)
Intel推出的基于集成眾核MIC架構(gòu)的至強(qiáng)融核系列產(chǎn)品是為了解決高度并行計(jì)算問(wèn)題。它基于x86架構(gòu),支持OpenMP、pThread等并行編程模型。英特爾MIC架構(gòu)具有更小的內(nèi)核和更多的硬件線程,以及更寬的矢量單元,是提高整體性能、滿足高度并行化應(yīng)用需求的理想之選[12]。
并行程序執(zhí)行時(shí),多線程之間相互通信會(huì)使程序運(yùn)行變得復(fù)雜,選擇合適的并行粒度才能最大限度地提高并行的效率。MRG32k3a并行化屬于細(xì)粒度并行,每線程單獨(dú)產(chǎn)生一段連續(xù)隨機(jī)數(shù)子序列,并發(fā)度高、占用資源較少、代碼較短、各線程間數(shù)據(jù)交換少,適合移植到MIC上運(yùn)行。
本文基于MIC的MRG3ak3a并行化實(shí)現(xiàn)分為三個(gè)步驟:首先,將串行程序使用OpenMP并行化,通過(guò)TestU01測(cè)試其隨機(jī)數(shù)序列的準(zhǔn)確性;再次,測(cè)試CPU上并行版本的性能,如果加速比不能隨著核數(shù)增加而線性增長(zhǎng),則需要對(duì)程序進(jìn)行優(yōu)化,使之發(fā)揮出多核的威力;最后,移植到MIC上進(jìn)行編譯選項(xiàng)篩選,Intel的各種優(yōu)化編譯選項(xiàng)在不同程度上會(huì)提升運(yùn)行效率,為最大發(fā)揮MIC性能,要選擇出最適合MRG32k3a并行程序運(yùn)行的編譯選項(xiàng),接著完成MIC上的性能測(cè)試。
2實(shí)驗(yàn)數(shù)據(jù)及性能分析
2.1TestU01測(cè)試分析
為保證并行化結(jié)果的正確性,本文選用均勻隨機(jī)數(shù)統(tǒng)計(jì)檢測(cè)庫(kù)TestU01進(jìn)行隨機(jī)數(shù)性能測(cè)試。TestU01相比Diehard,NIST等統(tǒng)計(jì)檢測(cè)庫(kù),其檢測(cè)最為嚴(yán)格,涉及216種、455個(gè)統(tǒng)計(jì)檢測(cè)。綜合SmallCrush、Crush、BigCrush的三大類測(cè)試結(jié)果,說(shuō)明了MRG32k3a串行與并行程序能夠全部通過(guò)TestU01測(cè)試。串行版本與4線程并行版本的TestU01測(cè)試的P-value統(tǒng)計(jì)分布情況,如圖2所示。圖2中串行版本P-value落在區(qū)間(0.08,0.92)之間比例為88.56%,4線程并行版本P-value落在該區(qū)間的比例為87.24%,通過(guò)的檢測(cè)比例基本相同。對(duì)串行和并行程序的測(cè)試數(shù)據(jù)進(jìn)行了雙樣本柯?tīng)柲Z夫-斯米爾諾夫KS(Kolmogorov-Smirnov)統(tǒng)計(jì)測(cè)試,P-value為0.6517,進(jìn)一步說(shuō)明它們測(cè)試數(shù)據(jù)近似服從相同分布。
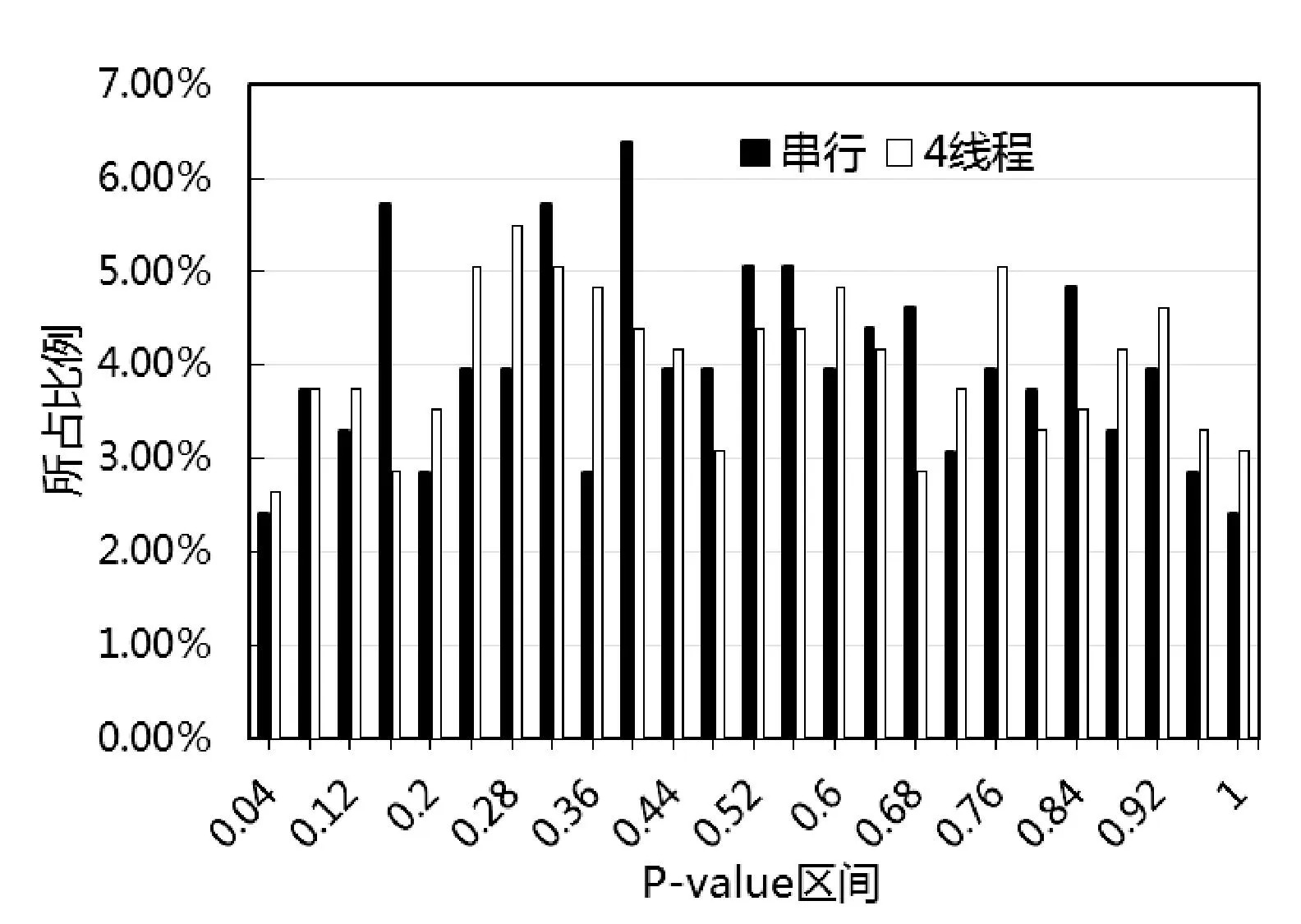
圖2 MRG32k3a串行與4線程并行程序TestU01測(cè)試的P-value統(tǒng)計(jì)分布
2.2基于CPU的并行化性能測(cè)試
實(shí)驗(yàn)環(huán)境:搭建的CPU平臺(tái)為兩個(gè)8核處理器Intel Xeon E5-2680 @ 2.7 GHz。
實(shí)驗(yàn)數(shù)據(jù)及分析:為更好地評(píng)估MRG32k3a程序的并行化成果,首先基于CPU進(jìn)行了基準(zhǔn)測(cè)試,在1、2、4、8、16線程情況下產(chǎn)生不同數(shù)量隨機(jī)數(shù)的時(shí)間測(cè)試結(jié)果如表1所示。其中產(chǎn)生同等數(shù)量隨機(jī)數(shù)的條件下,若線程數(shù)成倍增加,測(cè)試時(shí)間則成倍縮短;同等線程數(shù)條件下,若產(chǎn)生隨機(jī)數(shù)的數(shù)量成倍增加,測(cè)試時(shí)間也成倍增長(zhǎng);而且一定情況下,產(chǎn)生隨機(jī)數(shù)量越多其可擴(kuò)展性越好。圖3表示相應(yīng)線程下的加速比,橫軸為線程數(shù),縱軸為加速比,基于CPU的MRG32k3a并行化加速比與線程數(shù)呈線性增長(zhǎng),此時(shí)具有一定擴(kuò)展性,16線程時(shí)達(dá)到12.1609倍的加速比,而且在2、4、8線程時(shí)并行化效率接近100%,因此MRG32k3a并行程序可以移植到MIC。

表1 基于CPU的時(shí)間測(cè)試(s)
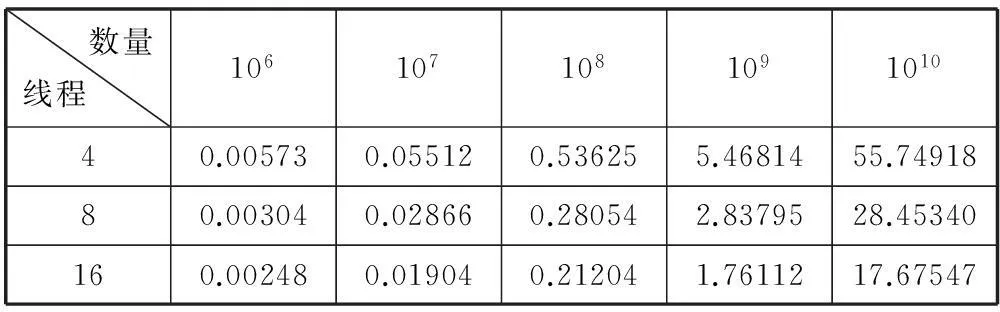
續(xù)表1
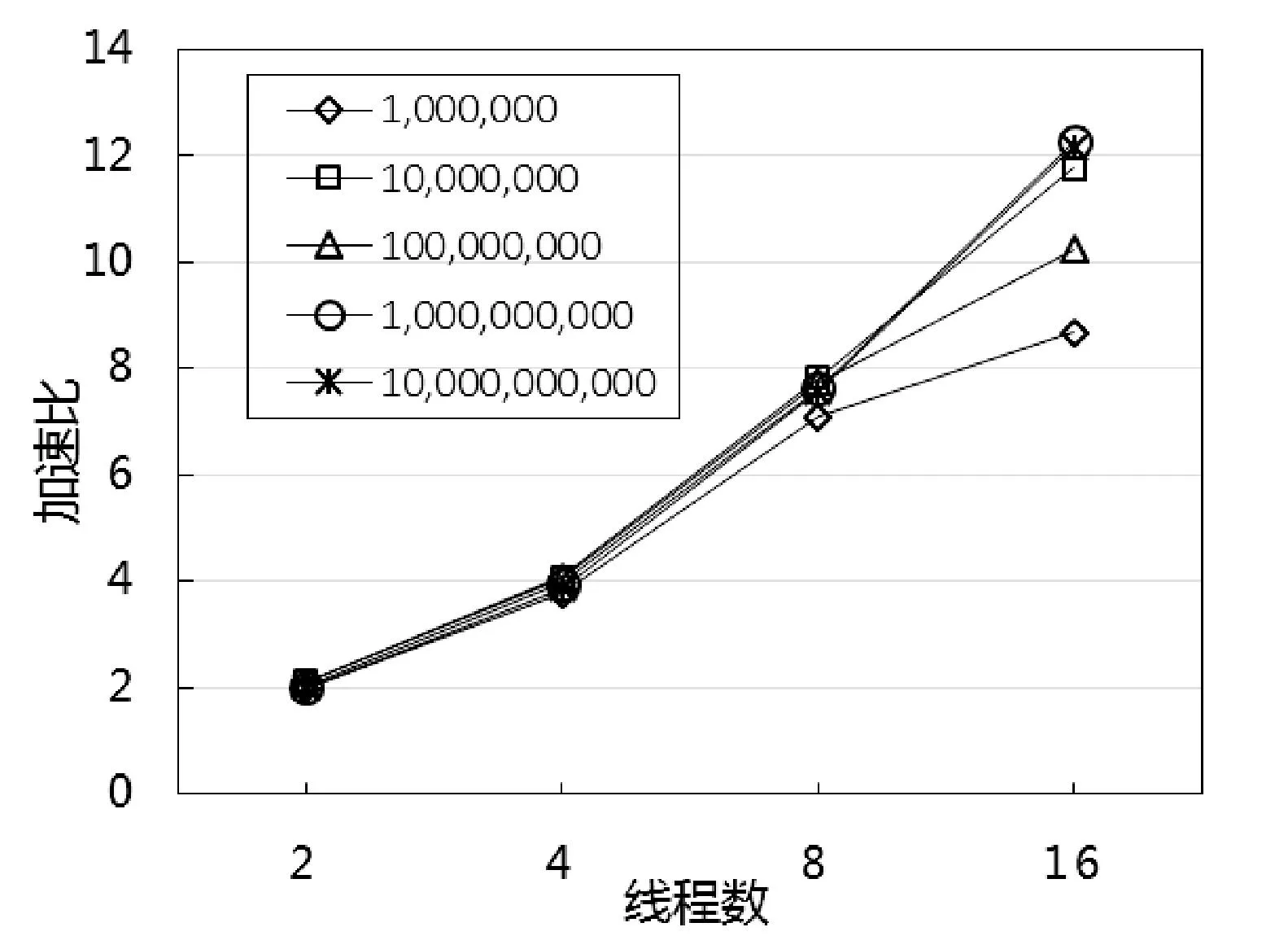
圖3 基于CPU的加速比趨勢(shì)圖
2.3基于MIC的并行化性能測(cè)試
實(shí)驗(yàn)環(huán)境:本文MIC平臺(tái)使用的是單個(gè)MIC卡Intel Xeon Phi 3110P 57cores @ 1.10 GHz,它含有57個(gè) x86 架構(gòu)指令集的核心,每個(gè)物理核心帶有4線程。
篩選優(yōu)化選項(xiàng):首先在224線程產(chǎn)生1010個(gè)隨機(jī)數(shù)情況下,依次添加不同編譯選項(xiàng)進(jìn)行時(shí)間測(cè)試,測(cè)試結(jié)果如表2所示,圖4為相應(yīng)的加速比。

表2 不同Intel編譯選項(xiàng)的時(shí)間測(cè)試(s)

圖4 不同編譯選項(xiàng)的時(shí)間測(cè)試加速比
如圖4所示,基于MIC并行化添加編譯選項(xiàng)-O3、-no-prec-div 、-fimf-domain-exclusion時(shí)加速比有所上升,優(yōu)化效果比較明顯。 其中-O3表明選用最高的優(yōu)化級(jí)別“3”,-no-prec-div指使用乘倒數(shù)替代除法來(lái)簡(jiǎn)化運(yùn)算,-fimf-domain-exclusion指排除與算法無(wú)關(guān)的浮點(diǎn)運(yùn)算,減少非正常浮點(diǎn)操作對(duì)性能的影響。
實(shí)驗(yàn)數(shù)據(jù)及分析:篩選出合適的編譯選項(xiàng)后,基于MIC平臺(tái)實(shí)現(xiàn)1、2、4、8、16、32、56、112、168、224線程產(chǎn)生不同數(shù)量隨機(jī)數(shù)序列的時(shí)間測(cè)試,測(cè)試結(jié)果如表3所示,圖5為相應(yīng)線程下的加速比。
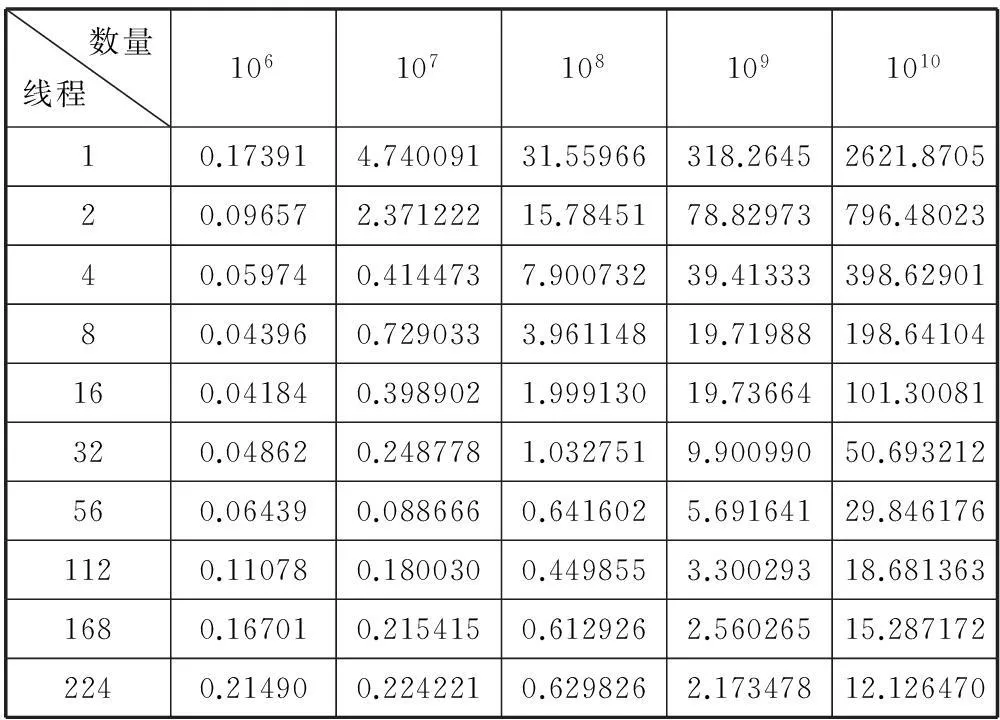
表3 基于MIC的時(shí)間測(cè)試(s)

圖5 基于MIC的加速比趨勢(shì)圖
如圖5所示,基于MIC的MRG32k3a并行化加速比效果也非常明顯,最大達(dá)到216.2105,部分線程的并行效率超過(guò)了100%。當(dāng)產(chǎn)生隨機(jī)數(shù)越多時(shí),提升效率越明顯。另外,在MIC卡上設(shè)置的線程數(shù)并不是越多越好,線程數(shù)太多,開(kāi)銷會(huì)比較大。因此要設(shè)置合適的線程數(shù)以確保MIC核的高利用率,比如圖5中基于MIC產(chǎn)生107個(gè)隨機(jī)數(shù)時(shí)在56線程左右的效率最好,多于56線程時(shí)加速比出現(xiàn)下滑趨勢(shì)。當(dāng)產(chǎn)生隨機(jī)數(shù)數(shù)量不斷增加,如產(chǎn)生1010數(shù)量的隨機(jī)數(shù),加速比逐漸呈線性狀態(tài),此時(shí)基于MIC也具有一定可擴(kuò)展性。
由于C++語(yǔ)言標(biāo)準(zhǔn)庫(kù)Boost、隨機(jī)數(shù)產(chǎn)生器庫(kù)SPRNG中沒(méi)有隨機(jī)數(shù)產(chǎn)生器MRG32k3a,本文選取了英特爾數(shù)學(xué)核心函數(shù)庫(kù)Intel MKL(Intel Math Kernel Library)中MRG32k3a的并行化結(jié)果進(jìn)行性能對(duì)比。如表4所示,測(cè)試數(shù)據(jù)來(lái)自文獻(xiàn)[10],平臺(tái)為Intel Xeon E5410,pts/s指每秒可產(chǎn)生的隨機(jī)數(shù)的數(shù)量,本文中基于MIC實(shí)現(xiàn)MRG32k3a并行化的最優(yōu)情況下每秒大約產(chǎn)生8.25E+08個(gè)隨機(jī)數(shù),而Intel MKL 基于Intel Xeon E5410平臺(tái)4線程情況下每秒大約也只能產(chǎn)生1.04E+08個(gè)隨機(jī)數(shù)。另外,對(duì)比表1中基于兩個(gè)8核CPU產(chǎn)生隨機(jī)數(shù)的時(shí)間,單個(gè)MIC卡相對(duì)CPU單線程的最佳加速比為17.73,說(shuō)明基于MIC實(shí)現(xiàn)MRG32k3a并行化具有一定優(yōu)越性,雖然MIC單核的計(jì)算
能力弱于同期的CPU,但利用眾核并行的優(yōu)勢(shì),加速比依然理想。
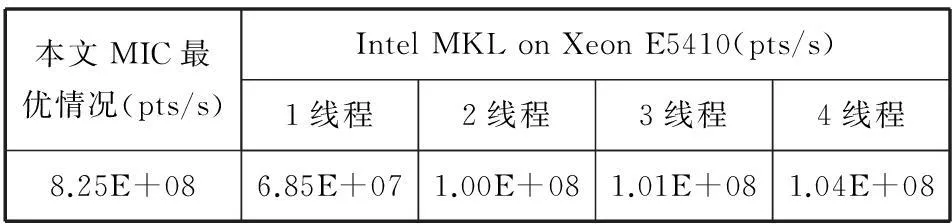
表4 與Intel MKL中MRG32k3a的性能對(duì)比
3結(jié)語(yǔ)
本文主要研究了隨機(jī)數(shù)產(chǎn)生器MRG32k3a利用“分而治之”思想的并行化實(shí)現(xiàn),將周期內(nèi)隨機(jī)數(shù)序列分段產(chǎn)生,并行程序全部通過(guò)了TestU01的455個(gè)測(cè)試,并基于MIC進(jìn)行時(shí)間測(cè)試和性能分析,最終加速比與線程數(shù)接近正比關(guān)系,部分線程并行效率超過(guò)100%,并具有一定擴(kuò)展性。與串行算法相比,基于MIC的MRG3ak3a并行化后,運(yùn)行效率得到極大改善,可廣泛應(yīng)用于高性能領(lǐng)域的科學(xué)研究。我們下一步工作將集中于使MRG32k3a并行算法更加完善,嘗試CPU+MIC協(xié)同并行化,也會(huì)繼續(xù)研究討論其它隨機(jī)數(shù)產(chǎn)生器并行化實(shí)現(xiàn)。
參考文獻(xiàn)
[1] Knuth D E.The Art of Computer Programming[M].Volume 2:Seminumerical Algorithms,1981.
[2] L’Ecuyer P.Random numbers for simulation[J].ACM Transactions on Modeling and Computer Simulation,1990,33(10):85-97.
[3] L’Ecuyer P,Blouin F,Couture R.A search for good multiple recursive random number generators[J].ACM Transactions on Modeling and Computer Simulation,1993,3(2):87-98.
[4] L’Ecuyer P.Combined multiple recursive random number generators[J].Operations Research,1996a,44(5):816-822.
[5] L’Ecuyer P.Good parameters and implementations for combined multiple recursive random number generators[J].Operations Research,1999,47(1):159-164.
[6] 陳國(guó)良.并行算法的設(shè)計(jì)與分析[M].北京:高等教育出版社,2002.
[7] Mascagni M,Srinivasan A.Algorithm 806:SPRNG:A scalable library for pseudorandom number generation[J].ACM Transactions on Mathematical Software,2000.
[8] Gao S,Peterson G D.GASPRNG:GPU accelerated scalable parallel random number generator library[J].Computer Physics Communications,2013,184(4):1241-1249.
[9] Marton K,Suciu A,Petricean D.A parallel unpredictable random number generator[C]//Roedunet International Conference (RoEduNet),2011 10th.Piscataway:IEEE,2011:1-5.
[10] Bradley T,du Toit J,Giles M,et al.Parallelization techniques for random number generators[J].GPU Computing Gems,2010:231-246.
[11] L’Ecuyer P,Richard Simard E,Jack Chen,et al.An object-oriented random number package with many long streams and substreams[J].Operations Research,2001,50(6):1073-1075.
[12] 王恩東,張清,沈鉑,等.MIC高性能計(jì)算編程指南[M].北京:中國(guó)水利水電出版社,2012.
[13] L’Ecuyer P,Simard R.TestU01:A C Library for Empirical Testing of Random Number Generators[J].ACM Transactions on Mathematical Software,2007,33(22):1-40.
[14] L’Ecuyer P,Simard R.On the performance of birthday spacings tests for certain families of random number generators[J].Mathematics and Computers in Simulation,2001,55(1-3):131-137.
中圖分類號(hào)TP311.52
文獻(xiàn)標(biāo)識(shí)碼A
DOI:10.3969/j.issn.1000-386x.2016.02.058
收稿日期:2014-06-02。陜西省自然科學(xué)基礎(chǔ)研究計(jì)劃項(xiàng)目(20 13JM8028)。宋博文,碩士生,主研領(lǐng)域:高性能計(jì)算。周津羽,研究員。華誠(chéng),工程師。劉逍,碩士生。周曉輝,教授。

