預計算類ECC標量乘算法高速存儲控制電路設計

李　博　王　威　嚴迎建　李　偉

(解放軍信息工程大學　河南 鄭州 450001)

?

預計算類ECC標量乘算法高速存儲控制電路設計

李博王威嚴迎建李偉

(解放軍信息工程大學河南 鄭州 450001)

摘要為提升橢圓曲線密碼體制中最耗時的標量乘運算的計算速度，解決采用預計算的快速實現算法中數據存儲問題，提取分析了NAF窗口算法、固定基窗口算法、固定基comb算法的存儲需求和共性特征，設計了適合ECC處理器的統一尋址電路和向量結構的高效訪存電路，有效支持目前具有預計算存儲需求的典型算法，并使得訪存效率和資源利用率大幅提升。在少量資源消耗下，與傳統存儲結構相比，訪問存儲性能提升達75%到95%。

關鍵詞橢圓曲線密碼標量乘預計算存儲結構

DESIGNING HIGH-SPEED STORAGE CONTROL CIRCUIT FOR ECC SCALAR MULTIPLICATION ALGORITHM WITH PRE-COMPUTATION

Li BoWang WeiYan YingjianLi Wei

(PLA Information Engineering University,Zhengzhou 450001,Henan,China)

AbstractIn order to improve computation speed of most time-consuming scalar multiplication operation in ECC and to solve data storage problem of fast implementation algorithm using pre-computation, we extract the common features and analyse the storage requirements in regard to NAF window algorithm, fixed base window algorithm, fixed base comb algorithm, design efficient access and storage circuit suitable for unified addressing and vector structure of ECC processor, which effectively supports for current typical algorithms with pre-computation storage needs, and significantly enhances the efficiency of access and storage and the resource utilisation. While the resource consumption is few, its performance of access and storage improves up to the range of 75% to 95% compared with traditional storage structure.

KeywordsElliptic curve cryptography (ECC)Scalar multiplicationPre-computationStorage structure

0引言

橢圓曲線公鑰密碼體制ECC以其運算速度快，占用資源少、單比特安全強度高等特點已成為公鑰密碼的新標準[1]。標量乘是橢圓曲線密碼算法的核心運算，決定著橢圓曲線密碼體制的運算速度，如何高效實現標量乘是當前研究的一個熱點。在眾多標量乘算法中，NAF窗口算法、固定基窗口算法、固定基comb算法等通過采用預計算，成為最具速度優勢的一類快速實現算法[2]。橢圓曲線密碼體制通常采用專用的ECC處理器進行實現。預計算數據帶來了額外的存儲資源以及數據頻繁訪問存儲的新問題，這也成為此類算法在處理器中適配的難點和瓶頸。

目前，許多研究者關注于算法本身，通過改進算法[3-6]，在保證速度的同時盡量降低存儲消耗。但是在算法適配中，依然不可回避資源消耗和數據頻繁訪問存儲問題。ECC處理器中通用的存儲結構并不適于這類算法的訪存需求，可能造成執行單元工作不流暢，將使算法實現效率降低。為解決存儲問題所導致的性能瓶頸，本文對上述三種采用預計算的標量乘快速算法進行了分析，提取預計算數據訪存的普遍特征，設計并實現了一種適于預計算標量乘算法的統一的尋址電路和向量結構的高效訪存電路，有效解決訪存效率問題。

1預計算標量乘算法分析

NAF窗口算法、固定基窗口算法、固定基comb算法是三種具代表性的標量乘算法，本節分別對三種算法進行分析，研究其預計算的特點。

1.1NAF窗口算法分析

非相鄰表示型NAF通過對密鑰k值重新進行NAF編碼，減少了k值中非零元素的個數，從而減少了標量乘算法的點加計算次數，提高了標量乘運算的速度[7]。窗口NAF標量乘算法如算法1所示。

算法1窗口NAF標量乘算法

輸出:kP。

2.對于i∈{1,3,5,…,2w-1-1}，計算Pi=iP。

3.Q=0。

4.對于i從l-1到0，重復執行

4.1.Q=2Q。

4.2.若ki≠0，則

若ki>0，則Q=Q+Pki。

否則，Q=Q- Pki。

5.返回(Q)。

從算法中易知，窗口NAF標量乘算法需要對窗口值內所有可能的奇數倍點進行預計算，如步驟2。預計算點的形式為iP，i∈{1,3,5,…,2w-1-1}。需要的存儲點個數為2w-2，這些點在步驟4.2中被調用參與運算，算法的期望運行時間為[1D+(2w-2-1)A]+[mD+(m/(w+1))A]，其中A表示點加運算，D表示倍點運算。

1.2固定基窗口算法

基點P固定的情況下，預計算不占用算法實現時間，采用預計算可獲得更高的運算速度，固定基窗口算法如算法2所示。

算法2固定基窗口標量乘算法

輸出:kP。

1.預計算Pi=2wiP，0≤i ≤d-1。

2.A=0，B=0。

3.對于j從2w-1到1，重復執行

3.1. 對于每個使Ki=j的i，執行：B=B+Pi。

3.2. A=A+B。

4.返回(A)。

固定基窗口標量乘算法需要對偶數倍點進行預計算，預計算點的形式為2wiP，0≤i ≤d-1，需要的存儲點個數約為d，這些點可能會在步驟3中參與運算，算法的期望運行時間為(2w+d-3)A。

1.3固定基comb算法

固定基comb標量乘算法也是針對基點P固定情況下的快速標量乘運算。comb標量乘算法如算法3所示。

算法3固定基comb標量乘算法

輸出:kP。

1.對于所有長度為w的二進制串(aw-1,…,a1,a0)，預計算[aw-1,…,a1,a0]P。

2.若需要，則用0填充k的左邊，記k=Kw-1//…//K1//K0，其中每個串Kj的長度為d。用Kij表示Kj的第i位。

3.Q=0。

4.對于i從d-1到0，重復執行

4.1. Q=2Q。

4.2. Q=Q+[Kiw-1,…,Ki1, Ki0]P。

5.返回(Q)。

comb算法對于所有可能的位串(aw-1,…,a1,a0)都要進行預計算 [aw-1,…,a1,a0]P，需要的存儲點個數為2w-1。這些點將在步驟4.2中參與運算，算法的期望運行時間為(((2w-1)/2w)d-1)A+(d-1)D。

NAF窗口算法、固定基窗口算法、固定基comb算法是三種各具代表性的算法，雖然都采用預計算，但預計算的數據不同，分別為基點的奇數倍點、偶數倍點和連續倍點，且計算量和存儲量也各不相同。NAF窗口算法適用于基點未知的情況，后兩種算法適于基點固定的情況。其共同特征是預計算的各點將依條件頻繁在算法核心步驟中被調用，且選點具有隨機性。這涉及到兩個問題：一是正確找到點的位置，即統一的尋址電路設計；二是快速存取，即高效讀寫電路設計。

2預計算標量乘算法存儲結構設計

為解決上節提出的問題，本節將對預計算數據的尋址和讀寫進行分析，并設計統一的尋址電路和向量結構的高效訪存電路。

2.1統一的尋址電路設計

統一尋址的理論依據來源于不同算法中的共性特征。分析可知，三種算法都需要根據某個特定值確定取點的位置，對于算法1，該值為步驟4.2中的ki；對于算法2，該值為步驟3.1中的i；對于算法3，該值為步驟4.2中的[Kiw-1,…,Ki1,Ki0]。這里統一用Rk表示。

P的一個坐標x或y占用的存儲單元數用VL=L/W表示，其中L為x或y的二進制表示長度，W為存儲單元的位寬。VL在尋址中的作用將在后面詳細描述。

接下來，將分別對三種算法提取尋址公式：

? NAF窗口算法

對于算法1：奇數倍點的存儲，在圖1中給出了該情況下的P值存儲形式。

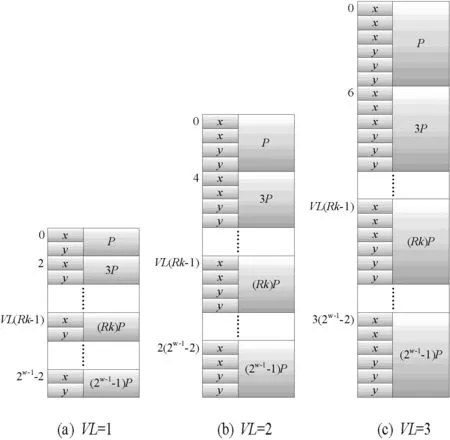
圖1　不同VL下P的奇數倍值存儲形式

算法1中存儲的點為{P,3P,…,(2w-1-1)P}，以順序的方式依次存儲。圖中(a)、(b)、(c)分別表示VL為1、2、3時的情況，并標出了各點的初始地址。對圖1的存儲方式，采用數學歸納法，提取出點的初始地址計算公式為VL*(Rk-1)，其中Rk∈{1,3,5,…,2w-1-1}。

? 固定基窗口算法

對于算法2：偶數倍點的存儲，在圖2中給出了該情況下的P值存儲形式。

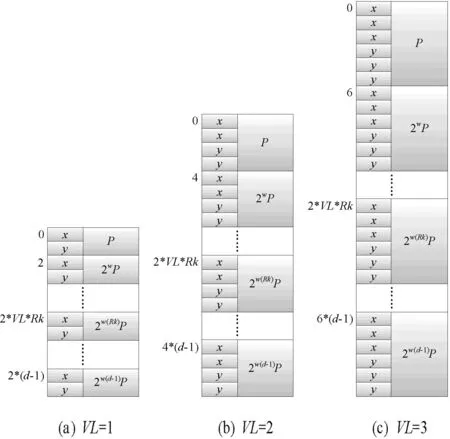
圖2　不同VL下P的偶數倍值存儲形式

算法2中存儲的點為{P,2wP,…,2w(d-1)P}，以順序的方式依次存儲。圖中(a)、(b)、(c)分別表示VL為1、2、3時的情況，并標出了各點的初始地址。對圖2的存儲方式，采用數學歸納法，提取出點的初始地址計算公式為2×VL×Rk，其中Rk∈{0,1,…,d-1}。

? 固定基comb算法

對于算法3：連續倍點的存儲，在圖3中給出了該情況下的P值存儲形式。

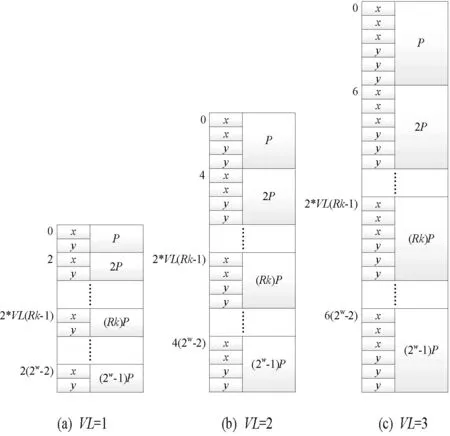
圖3　不同VL下P的連續倍值存儲形式

算法3中存儲的點為{P,2P,…,(2w-1)P}，以順序的方式依次存儲。圖中(a)、(b)、(c)分別表示VL為1、2、3時的情況，并標出了各點的初始地址。對圖3的存儲方式，采用數學歸納法，提取出點的初始地址計算公式為2×VL×(Rk-1)，其中Rk∈{1,2,…,2w-1}。

綜上得到三種算法的初始地址尋址公式如下：

奇數倍點尋址：VL×(Rk-1)；

偶數倍點尋址：2×VL×Rk；

連續倍點尋址：2×VL×(Rk-1)。

三個公式形式十分相近，可以采用統一的硬件完成，細微差別可通過設置模式選擇信號來確定。

2.2向量讀寫電路設計

解決尋址后另一個問題就是讀寫控制，對于普通讀寫電路，以VL=n為例，取一個點P的坐標x需要n條取數指令，并且要配合地址加一操作，共需要2n條匯編指令，耗費2n個時鐘周期。讀寫操作是頻繁的，因此迫切需要提高讀寫效率。

一個坐標x被分成n個分量 (x1, x2,…,xn)進行存儲。這種存儲具有向量操作的特點，適于采用向量結構的存儲單元[8]。向量操作是單指令多數據流(SIMD)的一種實現，是開發數據級并行性的有效模型[9]。一條向量指令對一組數據指定了相同的操作，相當于完成一個循環操作。向量操作的特點就是單指令多操作，對數據的讀取就需要用一條指令讀出完整長度的數據。每組數據之間相互獨立，不存在相關性，可以實現多個相同操作的并行執行。因此，本文引入向量操作，用一條指令完成存取，以提升取數效率，減少指令數，縮短存取時間。

用一條指令完成一組數據的存取，只需將讀寫使能信號根據向量長度VL保持n個有效周期，取出一個完整坐標x的n個分量，地址自增加1由硬件配合同步。由此，取點P的一個橫坐標x，指令數從2n條降為1條，周期數從2n降為n。

存取時間還存在進一步降低的空間：由于橢圓曲線密碼中的參數位寬較大，實現上通常采用小位寬的基本運算單元多次調用或級聯拼接來完成，通過流水分割解決數據間的相關性，如圖4所示。很多算法理論上支持這樣的拼接迭代，實際的算法實現上也通常采用這種策略，即第一組數據分量進入運算模塊后即開始運算，相當于存取數據的時間僅為第一個分量存取的時間，其他分量存取與執行時間重疊。因此存取時間進一步縮短至1個時鐘周期。

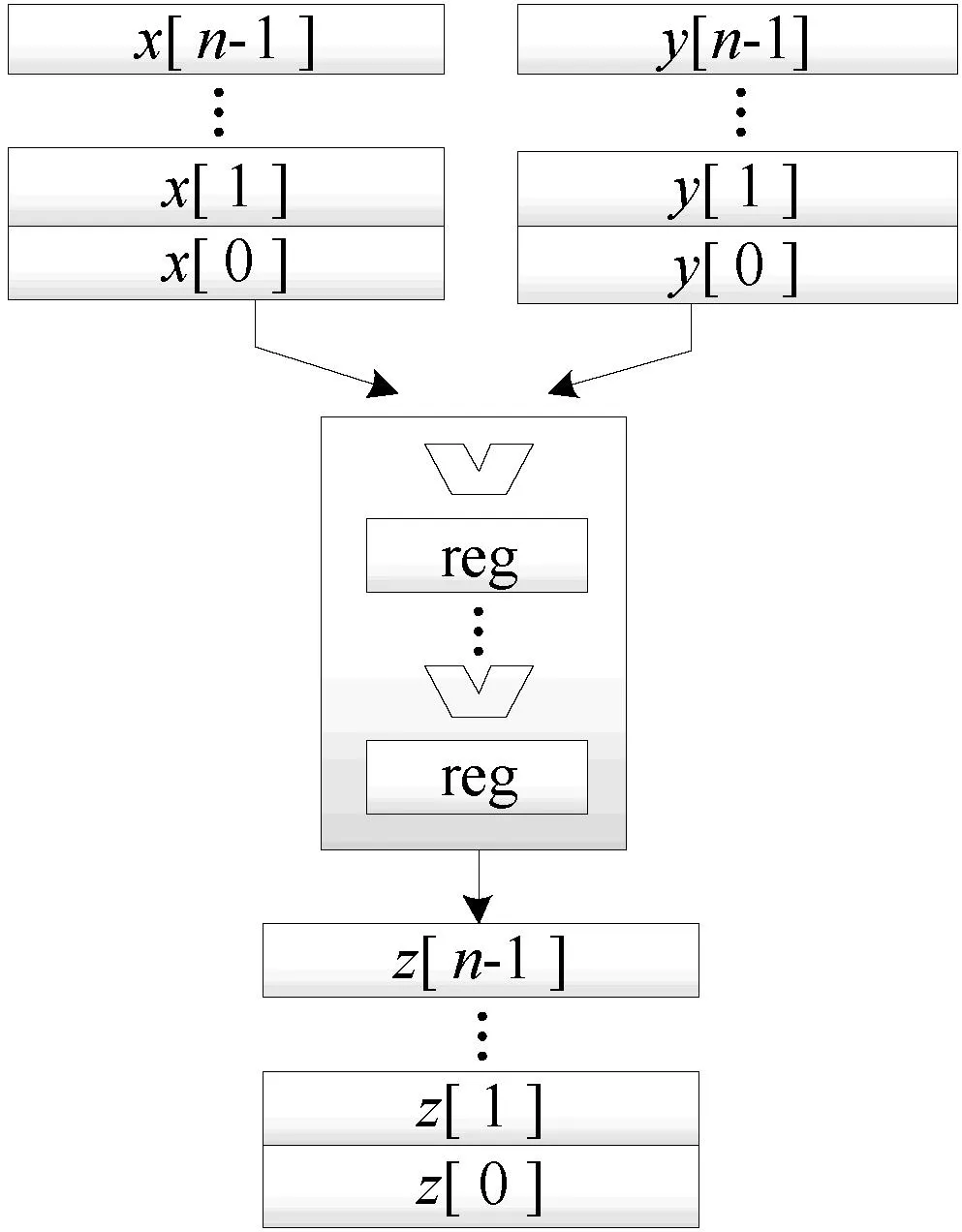
圖4　向量指令并行執行模式

2.3設計實現

統一尋址電路和向量讀寫電路如圖5所示。

圖5　向量指令并行執行模式

上半部分為向量使能EN_VL產生電路：初始使能信號EN高有效一個周期，表示開始向量操作，經過多級寄存器寄存后的延遲信號，在“*”單元中根據VL的值選擇性地進行“或”操作，得到一個保持VL個周期高有效的使能信號EN_VL，即向量使能信號；

下半部分為向量地址產生電路：虛框內為統一尋址電路，通過模式選擇信號Mode1和Mode0確定地址生成公式，即分別控制VL是否乘“2”和Rk是否減“1”，以滿足三種算法需求。生成的初始地址，在向量使能信號EN_VL高有效的前一個周期存入地址寄存器Addr_reg，向量使能EN_VL高有效的VL個周期中，Addr_reg在各周期內完成自加1操作，產生向量地址信號Addr。

統一的尋址和向量讀寫電路實現簡單，資源占用極少，卻可以帶來較高的性能提升。

3性能分析

本文的設計在性能提升上體現在兩方面：一是該結構支持預計算存儲，進而可以適配預計算類快速標量乘算法帶來的性能提升；二是向量結構使得指令數減少，訪問存儲時間縮短帶來的性能提升。

3.1支持預計算類算法所帶來的性能提升

首先，本文設計的向量存儲結構特別適合預計算類標量乘算法，能有效提高標量乘實現效率。三種算法在不同窗口長度w下性能提升程度不同，將其與未采用預計算的原始算法——“從左至右二進制”方法進行對照。在素域上，點加A計算量是倍點D計算量的1.4倍，據此得到各情況下算法期望運算時間與原始算法的百分比如圖6所示。

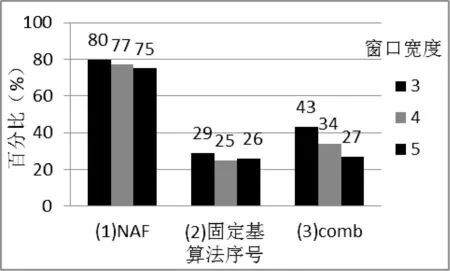
圖6　預計算標量乘算法性能提升

從圖6可以看出固定基類的算法計算量降低明顯，不過其存儲點的資源也較大；NAF窗口法計算量降低相對較小，但適用于非固定基的情況，存儲需求小。具體選用何種算法需綜合考慮性能和資源及應用需求。本文的設計結構對上述類型的算法均能夠較好地支持，性能提升范圍達20%至75%。

3.2存儲結構的性能提升

本文設計的向量結構存儲單元，在滿足算法需求的必要存儲資源基礎上，僅增加統一尋址和讀寫控制電路的少量資源，卻帶來了訪問存儲上性能的顯著提升。指令條數由2n降為1，間接降低了譯碼、數據相關等環節的硬件代價，在資源消耗上看，甚至是不增反減的。

訪問存儲時間的提升十分明顯，消耗時鐘周期數最大可從2n降為1。以NIST推薦的3種長度橢圓曲線為例，選取長度分別為256、384、521 bit的三類曲線，存儲單元基本位寬選用32、64、128 bit，圖7中給出了各種情況下的采用向量結構訪存時間占普通結構訪存時間的百分比。

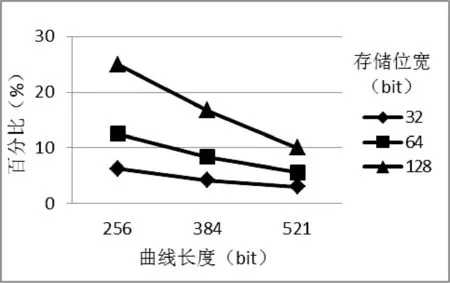
圖7　向量結構訪存時間占原時間的比率

可以看出，在存儲單元位寬相同時，曲線長度越大，訪存時間占原時間的比率越小，進而性能提升比率越大；在曲線長度一定時，存儲單元位寬越越小，訪存時間占原時間的比率越小，進而性能提升比率越大。存儲單元位寬的選取應綜合考慮各種因素，適合具體應用需求，總體來說，與傳統的存儲結構相比，節省訪問存儲時間達75%至95%。

4結語

本文通過對多種預計算類標量乘算法進行分析，提取預計算數據的訪存特點，設計了向量結構的存儲結構。統一尋址電路和高效的讀寫電路有效提升了該類算法訪存效率，有效減少指令條數，降低譯碼等硬件代價，減少了循環控制開銷，并極大地縮短了存取時間。

參考文獻

[1] Hankerson D,Vanstone S,Menezes A J.Guide to elliptic curve cryptography[M].Springer,2004.

[2] 劉斌,瞿新南.橢圓曲線密碼體系中標量乘的快速算法研究[J].計算機安全,2013(6):13-16.

[3] Daiyuan B.低存儲需求的快速標量乘法算法[J].計算機工程,2012,38(4):137-139.

[4] 劉國柱,祁華欣.優化的低存儲NAF標量乘算法[J].科學技術與工程,2013,13(19):5683-5686.

[5] 王玉璽,張串絨,張柄虹.一種改進的固定基點標量乘快速算法[J].計算機科學,2013,40(4):135-138.

[6] 蔣洪波,吳巖,馮新宇,等.基于NAFw的二進制域乘法算法[J].重慶工商大學學報:自然科學版,2012,29(6):47-49.

[7] 趙前進,李西萍,戴紫彬,等.NAF標量乘算法的并行計算研究[J].電子技術應用,2010(7):160-162.

[8] 王永文,陳微,鄭倩冰,等.多線程向量處理器中向量數據存儲結構的設計與實現[J].計算機研究與發展,2012(1):53-55.

[9] 楊曉輝.橢圓曲線密碼專用指令協處理器研究[D].河南:解放軍信息工程大學,2011.

中圖分類號TP309.7

文獻標識碼A

DOI:10.3969/j.issn.1000-386x.2016.02.075

收稿日期：2014-05-27。李博，碩士生，主研領域：專用集成電路設計。王威，碩士生。嚴迎建，副教授。李偉，講師。