魚群互利共生動力學模型的穩定性分析

王斌斌熊煥煥張海亮（浙江海洋學院，浙江舟山316000）

?

魚群互利共生動力學模型的穩定性分析

王斌斌熊煥煥張海亮
（浙江海洋學院，浙江舟山316000）

摘要：通過對經典種群動力學模型的改進，建立了互利共生魚群的動力學模型。利用非線性微分方程穩定性理論,得到了互利共生魚群動力學模型的平衡點，并對其平衡點進行了穩定性分析。文章最后從魚群的演化角度解釋了相應的變化過程。

關鍵詞：互利共生；動力學模型；穩定性

1引言

關于種群問題，Malthus在《人口原理》一書中提出著名的Malthus人口模型，荷蘭生物學家Verhulst建立了logistic模型，這些模型都準確的預測了當時的人口數量變化。那么，對于海洋中的魚群而言，是否可建立類似的模型來探討魚群的變化規律呢？

20世紀40年代，Lotka和Volterra建立了種間競爭關系的理論基礎，提出了著名的Lotka-Volterra模型，為魚群及其它種群問題的研究開辟了新的模型研究方式。在魚群生態系統里，一般研究具有捕食關系的魚群競爭模式與非捕食關系的魚群競爭模型，且后者更具有普遍性。在非捕食的關系中，研究者對種群的相互競爭做了大量的研究，但缺少對互利共生方面的動力學模型的研究，為此有必要去建立魚群互利共生的動力學模型來探討海洋中魚群的數量變化規律。

2互利共生模型的建立

海洋捕撈者都希望掌握或了解魚群的變化規律，甚至希望某些魚群能夠按照他們意愿而發生相應的變化，這樣有利于獲得最大的經濟價值。通過建立魚群動力學模型來分析魚群隨時間的演化規律，預測它們的發展趨勢，是一種常用的方法。本文通過改進Lotka-Volterra模型，建立互利共生魚群的動力學模型。

對于魚群甲，當魚群乙在同一區域生存時，由于兩個魚群之間互利共生，勢必會促進魚群甲的增長。即魚群乙的存在對魚群甲的增長產生積極的影響，需要對lo?gistic模型增加了互利共生的項，給出了類似Lotka-Volt? erra模型的模型。

我們給出的魚群甲的動力學方程為

類似魚群甲，魚群乙互利共生的動力學方程：

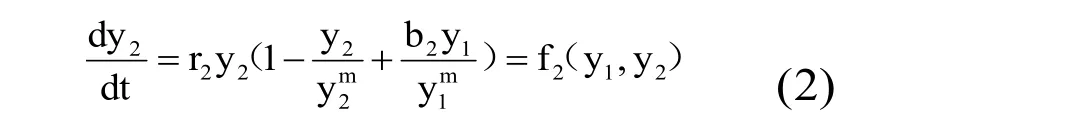
在logistic模型的基礎上，通過引進互利共生項，并且用b1、b2來具體刻畫魚群互利共生的強弱機制，建立了合理的魚群互利共生的動力學模型(1)、(2)。

3魚群模型的穩定性分析

所建立的魚群互利共生模型在什么情況下保持系統的平衡？如何使魚群在一個相對平衡的狀態下生存？這可以通過對上述給出的互利共生的模型(1)、(2)穩定性分析來得到。

模型(1)、(2)的平衡態方程為

由式(3)可求得4個平衡點：

下面分別對這些平衡點討論它們的各自的穩定性。求導計算得：

對于魚群的平衡態A1(0,0)，代入(4)式可得

特征方程為

對應的特征方程的解為

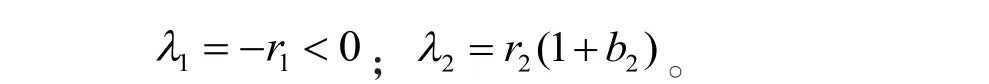
如果b2< -1，那么平衡態為穩定的結點。如果b2> -1，那么平衡態為不穩定的鞍點。

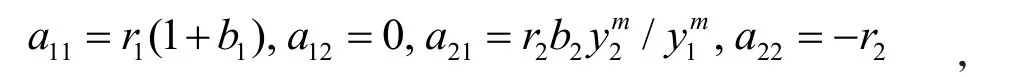
對應的特征方程的解為

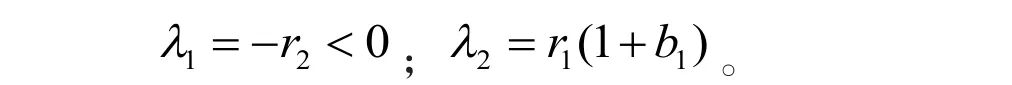
1點。如果b1> -1，那么平衡態為不穩定的鞍點。

對于魚群的平衡態

A4((1+b1)/(1-b1b2),(1+b2)/(1-b1b2))，代入(4)式得

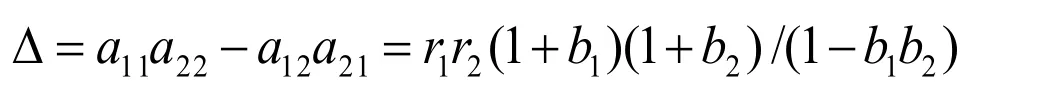
4結論

本文建立了互利共生魚群的動力學模型，求出了其4個平衡態點，并且討論了它們各自的穩定性。當兩個魚群在海洋中生存時，它們的演化規律有如下幾條：

1、當b1> -1，b2> -1，即二種魚群為雙方各自提供生長資源時，兩種魚群互相促進兩種魚群的生長，互相的存在有利于它們的生長。隨著時間的變化，整個魚群將會向A4演化，達到雙方共存的穩定的狀態。

2、當b2< -1或b1> -1時，乙魚群的存在，增加了甲魚群生成資源，而甲魚群的存在，減少了乙魚群生長資源。因此魚群乙的存在促進了魚群甲的生長，魚群甲的存在抑制了魚群乙的生長，整個魚群將會向A2演化。

3、當b1< -1或b2> -1時，即乙魚群的存在，減少了甲魚群的生成資源，而甲魚群的存在，增加了乙魚群生長資源。魚群乙的存在抑制了魚群甲的生長，魚群甲的存在促進了魚群乙的生長，整個魚群將會向A3演化。

4、當b1< -1，b2< -1時，，A4為鞍點，兩種魚群互相的減少原有資源，兩個魚群互相之間達不到促進的作用，整個魚群將遠離A4。

基金項目：浙江省大學生科技創新活動計劃（新苗人才計劃）項目立項資助項目（2015R411035）

中圖分類號：U693+.9

文獻標識碼：A

文章編號：1006－7973（2016）01－0075－02