圖像畸變校正算法在測量中的應用

河南省計量科學研究院　劉賓武　張　燕　鄭開放

?

圖像畸變校正算法在測量中的應用

河南省計量科學研究院劉賓武張燕鄭開放

【摘要】工業(yè)用鏡頭對物體進行取像時，物體會產生畸變失真。畸變對物體參數(shù)的后續(xù)測量產生影響，所以必須對畸變圖像進行校正。本文通過對已有圖像畸變校正算法的介紹比較，采用了一種不拘泥于具體鏡頭，適用性強的校正算法。此算法首先根據(jù)畸變圖像產生的原理對徑向畸變建立模型，算法第一步使用亞像素邊緣算法對失真圖像定位邊緣、提取邊緣點；第二部用最小二乘法對提取的邊緣點進行線性擬合，得到所有點與標準點的總平方和；第三步使用LM算法對第二步得到的總平方和進行優(yōu)化參數(shù)處理，得到最優(yōu)參數(shù)；第四步將最優(yōu)參數(shù)帶入反校正模型，最終還原圖像。還原后的圖像與標準圖像相比，校正結果的精度可以達到1個像素的最大誤差。

【關鍵詞】廣角鏡頭；徑向失真；亞像素；LM算法

0　引言

在工業(yè)測量領域中，電子元器件針腳距離的自動化檢測是一大應用。針腳距離的自動化檢測首先要求對針腳進行取像，廣角鏡頭由于其價格低、視場大而應用廣泛。由于成像系統(tǒng)和特定的生產環(huán)境造成的影響，拍攝后的圖像產生畸變，不利于后續(xù)處理。廣角鏡頭取像的特點：鏡頭焦距距離拍攝物體距離越近，失真越大；距離越遠，失真越小。但遠距離的拍攝會收到各種光源的影響，造成拍攝不清。失真類型為徑向失真。

廣角鏡頭（工業(yè)使用）所造成圖像坐標點位置的像素誤差大致在2-12個像素之間，如賓得（PENTAX)公司生產的焦距為8mm的工業(yè)鏡頭，其在近距離拍攝圖像時會產生3個像素左右的失真。圖像的畸變校正可以從兩方面考慮，硬件的改進和軟件的優(yōu)化。一般來說，硬件改進的成本較高，實現(xiàn)起來困難。但軟件不同，軟件改進起來容易且容易實現(xiàn)，最重要的是軟件可以降低企業(yè)的成本，利于推廣。本文首先對現(xiàn)有校正模型算法進行分析，然后采用了一種徑向畸變圖像校正模型來校正圖像以及完成軟件實現(xiàn)，為工業(yè)中的自動化測量提供參考，此算法的特點：通用性強，不限制于具體鏡頭。

1　圖像畸變算法介紹

目前最常用的畸變校正算法主要有模板法和基于參數(shù)已知——等效球面法。

模板法原理：首先做好一個理想的模板，對模板取像，然后對理想模板和成像模板上標定對應點，為對應點建立數(shù)學畸變模型，計算出模型的各個參數(shù)，最后將完整的畸變圖像代入數(shù)學模型，完成圖像還原。模板法包括棋盤格模板法[1]和同心圓模板法[2]。模板法優(yōu)點是精度高，但算法需要制作理想模板，數(shù)學計算量大，實時性低。

基于參數(shù)已知——等效球面法[3]原理：采用等效球面模型來模擬圖像畸變，需要提取鏡頭的水平角度、垂直角度以及焦距的大小，利用上述參數(shù)可以完成圖像的畸變校正。計算量小。其優(yōu)點是無需對各種鏡頭提取模板，只用知道鏡頭的水平角度、垂直角度以及焦距，就可以還原畸變的圖像，算法簡易實現(xiàn)。但在確定其鏡頭參數(shù)時存在誤差，導致算法精度不高。

基于上述兩種畸變校正模型優(yōu)缺點考慮，下面介紹一種通用性強、不限制于具體鏡頭的畸變校正模型系統(tǒng)。通過實驗結果證明，此校正算法的精度為一個像素。

2　徑向畸變校正系統(tǒng)的建立

2.1算法設計

2.1.1建立徑向畸變校正模型

基于廣角鏡頭，建立徑向失真模型[4]。令標準圖像（圖1）的邊緣點的坐標為(x,y)，畸變圖像（圖2）中的對應點（邊緣紅點）的坐標為（），令圖像的長、高為W和N，令xc=W/2，yc=N/2，中心點坐標為（xc,yc)，公式如下：

圖1　標準圖

圖2　畸變圖

其中L(r)是關于半徑r的多項式。

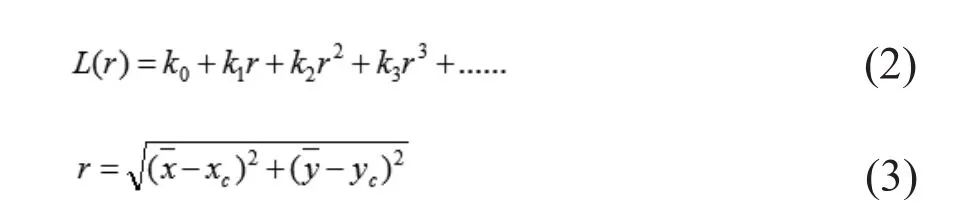
k0，k1，k2，...是模型參數(shù)。關于L(r)最高次的確定，我們選取偶數(shù)項（k0，k2，k4）作為畸變模型參數(shù)，實驗結果表明，選取偶數(shù)項比選取奇數(shù)項（k1，k3）建立的模型效果更好。多項式的最高次數(shù)越高，校正效果越精確，但會導致計算量增加。實驗表明，選取就可以達到要求的精度，計算量低。

2.1.2算法步驟

(1)用亞像素[5]邊緣算法對畸變圖像進行邊緣定位，提取邊緣點；

(2)將提取的邊緣點集失真模型公式(1)中，對參數(shù)k做初始化，得到校正點集；

(3)對校正點集做直線擬合處理，得到直線擬合方程L；

(4)將校正點集到直線L的距離的總平方和作為誤差，初次的誤差當做初始值；

(5)使用LM參數(shù)算法優(yōu)化參數(shù)k，得到最優(yōu)k；

(6)將k代入反校正算法模型，還原圖像（如圖3所示）。

圖3　算法流程圖

2.2軟件界面設計（如圖4所示）

2.3界面部分按鈕的簡介

Image：打開圖片；亞像素檢測：對選取的畸變圖像進行邊緣取點；求解畸變參數(shù)：將取到的邊緣點代入校正模型，進行參數(shù)k最優(yōu)化處理；重構圖像：將參數(shù)k代入反校正模型，還原圖像。

圖4　軟件概覽圖

3　實驗結果與分析

本文從定性和定量兩方面對實驗結果進行分析。

3.1 定性分析（如圖5所示）

3.2定量分析

實驗圖像的選取：不同程度畸變的四張圖像，通過軟件運行還原圖像，以均方誤差E和最大距離d兩個參數(shù)作為實驗結果。

3.2.1實驗圖片的選取

圖6　 標準圖與畸變圖的對比圖

如圖6所示，實驗圖像選取四張畸變程度大小不同的圖像，最大距離d與最小距離d描述標準圖和畸變圖，如表1所示，以像素為單位：

表1　畸變程度不同的四幅圖

3.2.2 求解最優(yōu)參數(shù)k

圖7　邊緣點示例圖

如圖7所示，對畸變圖像進行亞像素邊緣定位取點，每條邊選取200個點，總共800個點帶入畸變校正算法模型，運行算法得到最優(yōu)參數(shù)k。如表2所示，系數(shù)k保留小數(shù)點8位：

表2　最優(yōu)參數(shù)

3.2.3 定量分析

均方誤差E：將校正后的圖像的左邊緣選取的380個點與對應的標準圖像的380個點進行求均方誤差運算，由于本實驗為測量兩直線的距離，所以只計算x水平方向的均方誤差E。公式如下：

說明：標準圖像的最外邊緣矩形的左上角的點坐標為(128，48)，將校正后的圖像的最外邊緣矩形邊的坐標與標準圖像進行計算。

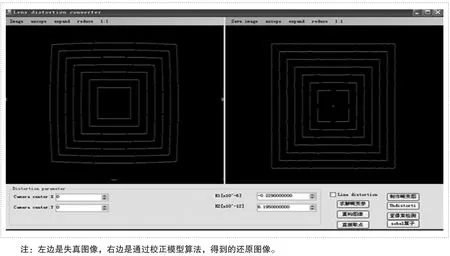
圖5　實驗結果圖

四幅圖的均方誤差與最大最小距離如表3所示，單位（像素），小數(shù)點保留到后六位：

圖8所示是四幅還原圖像與標準圖像的對比分析圖。

表3　校正結果

圖8　效果對比圖

說明：圖8是我們以標準圖最左邊緣的像素坐標與四幅校正圖最左邊線進行對比的實驗結果圖（y坐標不變，x坐標有誤差），標準圖像外邊緣上角坐標(128,48)，下角坐標為(128,432)。從圖8上看出還原后的圖像與標準圖像的像素位置相比，x坐標最小誤差為0.05個像素，最大誤差為0.53個像素，還原圖像精度為1個像素。

4　總結

上述實驗結果表明，此畸變校正系統(tǒng)精度較高。相比于現(xiàn)有其他校正算法，此算法具有不拘泥于具體鏡頭、適用性廣的特點，不足之處在于算法運行時間較長，需要繼續(xù)優(yōu)化。此算法可應用到廉價的廣角鏡頭中代替昂貴的鏡頭，降低企業(yè)成本。在工業(yè)自動化測量中，此算法可為工業(yè)中物體參數(shù)的測量，如元器件針腳距離的自動測量提供參考。

參考文獻

[1]湯旭濤.廣角攝像頭視頻圖像實時校正系統(tǒng)設計[碩士學位論文].上海:華東師范大學,2009.

[2]盛琳陽.基于圓序列的多幀對齊和徑向畸變校正算法[J].計算機應用與工程,2006(15).

[3]王偉,鐘堰利.廣角鏡頭圖像畸變校正系統(tǒng)的研究[J].光學技術,2004(4).

[4]王茂義,王睿.一種校正圖像邊緣的改進算法[J].儀器科學與光電技術,2006.

[5]李慶利.一種基于多項式插值改進的亞像素細分算法[J].2008.

[6]楊文茂,李全英.空間解析幾何[M].1997.