基于數據場和單次劃分的聚類算法

張　霓，陳天天，何熊熊

(浙江工業大學 信息工程學院，浙江 杭州 310023)

?

基于數據場和單次劃分的聚類算法

張霓，陳天天，何熊熊

(浙江工業大學 信息工程學院，浙江 杭州 310023)

摘要：針對現有大部分聚類算法普遍存在聚類質量不高、算法參數依賴性大、聚類類別個數和聚類中心無法準確確定等問題，在此提出了基于數據場和單次劃分的聚類算法(DF_SPCA).該算法通過分析數據的分布特征，引入數據場理論，在分析每個數據對象的距離和勢值分布圖的基礎上確定聚類中心.等聚類中心確定后，其余數據點在比自身勢值更高的數據點中找到與其距離最小的數據點，將類標與該數據點保持一致，從而實現單次劃分.最終算法在多個數據集上進行性能測試，并與其他聚類算法進行比較.實驗結果證明：DF_SPCA具有較高的聚類質量，能夠有效處理任意形狀的簇.

關鍵詞：數據場；數據聚類；勢值；聚類分析；勢值-距離分布

聚類的目的是根據物理對象或者抽象對象之間的相似性將數據集劃分成多個不同的類簇，使形成的同一個類簇中的對象具有較高的相似度，而不同簇中的對象相似度較低[1].聚類技術在文本分析[2]和模式識別[3]等諸多領域[4-7]都有廣泛的應用前景，在現有的聚類算法中，基于劃分的方法是一種被廣泛使用的聚類算法，其基本思想是通過預設聚類數目，然后隨機選擇聚類中心，通過迭代不斷優化目標函數，直至獲得最優目標函數時完成聚類.代表算法有K-means[8]和FCM[9]等.這類算法的優點在于簡單有效，易于操作，但由于算法需要預設聚類個數，對原始數據聚簇的分布形態有極大的影響，同時算法還存在聚類結果對初始簇類中心選擇敏感、對噪聲適應性差、不能發現任意形狀的簇等缺點.基于密度的方法主要是針對任意形狀的簇的發現而提出的，其基本思想是通過預設參數來發現數據密集區域，確定核心點，再利用核心點確定密度相連的對象實現聚類，獲得最終的聚類結果.代表算法有DBSCAN[10]和OPTIC[11]等等.這類算法的主要優點是具有良好的可擴展性，能夠處理任意形狀的簇，對于噪聲數據是健壯的，但是聚類結果的優劣對參數的依賴性較強，通常需要經驗設定.

有些算法[12-17]將數據場理論與傳統聚類算法相結合來實現聚類；文獻[13，15]將數據場理論與劃分算法K-means,PAM等相結合，利用勢分布函數獲取初始的聚類中心，提高了聚類質量和收斂速度，但保留了基于劃分算法需要預設聚類個數和對離群點敏感的缺點；文獻[18]提出了一種基于數據場的密度聚類算法DF_DBSCAN，結合勢函數分布改進DBSCAN的聚類過程，提高了聚類準確率，但同時增加了算法的復雜度，且保留了DBSCAN算法對參數敏感性強的缺陷.針對上述問題，在此提出了一種基于數據場和單次劃分的聚類算法(DF_SPCA).計算每個數據對象的勢值和距離值，作出勢值與距離的分布圖，根據聚類中心具有較高勢值，且被較低勢值的其他數據點包圍的特性確定聚類中心，無需預設聚簇的個數，同時能夠自動聚類中心的位置.等聚類中心確定后，將其余點按到最近鄰的更高勢值對象的最小距離進行劃分，該過程只需單次掃描，不需要迭代運算.實驗結果表明：DF_SPCA算法有較好的聚類性能，能夠實現對任意形狀的簇聚類.

1數據場理論

場的概念是英國物理學家法拉第在1837年第一次提出，用于描述物質粒子之間存在的非接觸相互作用.隨著場理論的發展，場的概念被抽象描述為一個數學概念，用來描述某個數學函數或物理量在空間中的分布規律.數據場理論[8]借鑒了物理學中場的思想，將其場的描述方法和物質粒子間的相互作用引入到抽象的數據空間中.該理論用勢函數來描述數據對象之間多對一的相互關系，克服了傳統數據聚類算法中只考慮對象之間一對一作用關系的缺陷，認為空間中任意點的狀態是其他所有對象共同作用的結果[18-20].

考慮到高斯分布的普適性以及短程場作用更有利于揭示數據分布的聚簇特性，將數據場勢函數[8]定義如下：

定義1已知數據空間Ω?Rd上的對象集合D={x1,x2,…,xi,…,xn}及其產生的數據場，則任意對象x∈D的勢函數描述為

(1)

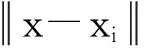
為了分析單數據對象產生的數據場中場強與距離的分布關系，假設mi=1，可得到具體關系如圖1所示.

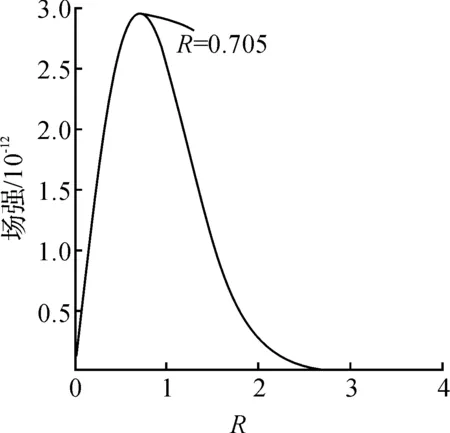
圖1　單數據對象數據場中場強與距離的分布關系Fig.1　The distribution of field intensity and distance in the data field of a single data object

當距離數據對象0.705σ時，場強達到了最大值，即以場源對象為中心，半徑為0.705σ的球面上存在很強的作用力指向場源對象.而當距場源對象的距離大于R≈2.121σ時，場強函數很快衰減為0，指示著短程場作用.因此，數據空間內的任意對象主要受其R≈2.121σ鄰域空間內的數據點影響作用，為了減小計算復雜度，將數據場勢函數定義進行修改.

定義2已知數據空間Ω?Rd上的對象集合D={x1,x2,…,xi,…,xn}及其產生的數據場，則任意對象x∈D的勢函數描述為

(2)

式中p為數據空間內對象x以半徑為R≈2.121σ所形成的鄰域空間內數據對象的數目.

數據場理論具有較好的刻畫數據和反映數據間多對一作用關系的能力，能夠對聚類算法獲得數據原始聚簇分布有較好的指導作用.

2基于數據場和單次劃分的聚類算法

2.1　主要思想

通過結合數據場理論對數據集中的數據對象分析，根據定義2計算每個數據對象的勢值，勢值越大的數據對象，說明其R≈2.121σ半徑內的數據對象越多，且距離該數據對象的距離越近，因此該點很大程度上是該簇類集合的中心.而勢值很小的數據對象，說明其R≈2.121σ半徑內的數據對象較少，說明該點很可能是游離在外的離群點對象.如圖2所示，x和y代表數據對象在二維空間的坐標，而z代表其在空間內的勢值強度，可以發現該數據存在4個簇類，且每個簇類的中心位置的勢值強度最大，越邊緣的數據對象的勢值強度越小.另外，簇中心與簇中心的距離較大，而簇內的數據對象到簇中心的距離較小.

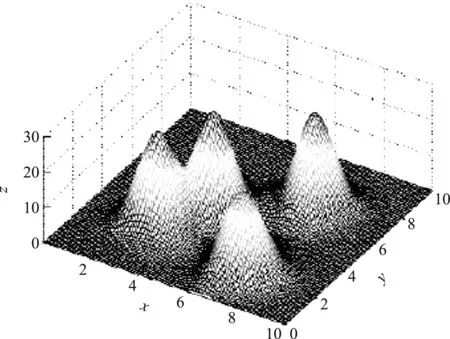
圖2　數據場示意圖Fig.2　Sketch map of data field

DF_SPCA算法主要基于以下兩點規律:

1) 簇類中心被具有較低勢值的鄰居點包圍，且與具有更高勢值的其它數據對象有相對較大的距離.

2) 噪聲點具有相對較小的勢值，且與勢值較高的數據對象有相對較大的距離.

對于任意一個數據對象xi，需要計算兩個量：數據對象的勢值φ(xi)和到具有更高勢值的其它點的最小距離δi.數據對象的勢值φ(xi)可以根據定義2計算得到.

定義3對于任意數據對象xi，其到具有更高勢值的其他數據對象xj的最小距離δi定義為

(3)

式中dij為兩個數據對象xi和xj之間的距離.

對于具有最高勢值的數據點xi，定義δi為該數據點到數據對象xj的距離的最大值，即δi=maxj(dij).

存在人造樣本數據集DataSet1，其數據對象由二維數值屬性x和y描述，其數值僅表示數據對象在二維空間中的位置分布，DataSet1數據集在二維空間內的數據分布如圖3所示.

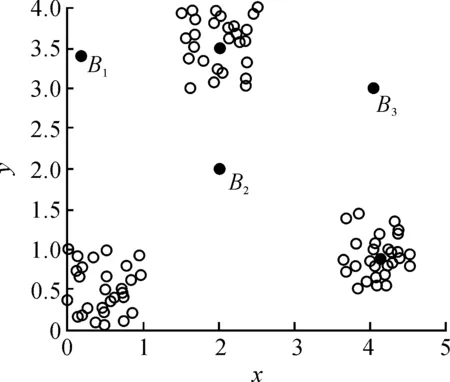
圖3　樣本DataSet1數據分布圖Fig.3　Data distribution map of sample DataSet1

計算樣本數據集中每個數據對象xi的勢值φ(xi)和到具有更高勢值的其他點的最小距離δi，作出φ(xi)和δi的分布圖如圖4所示.

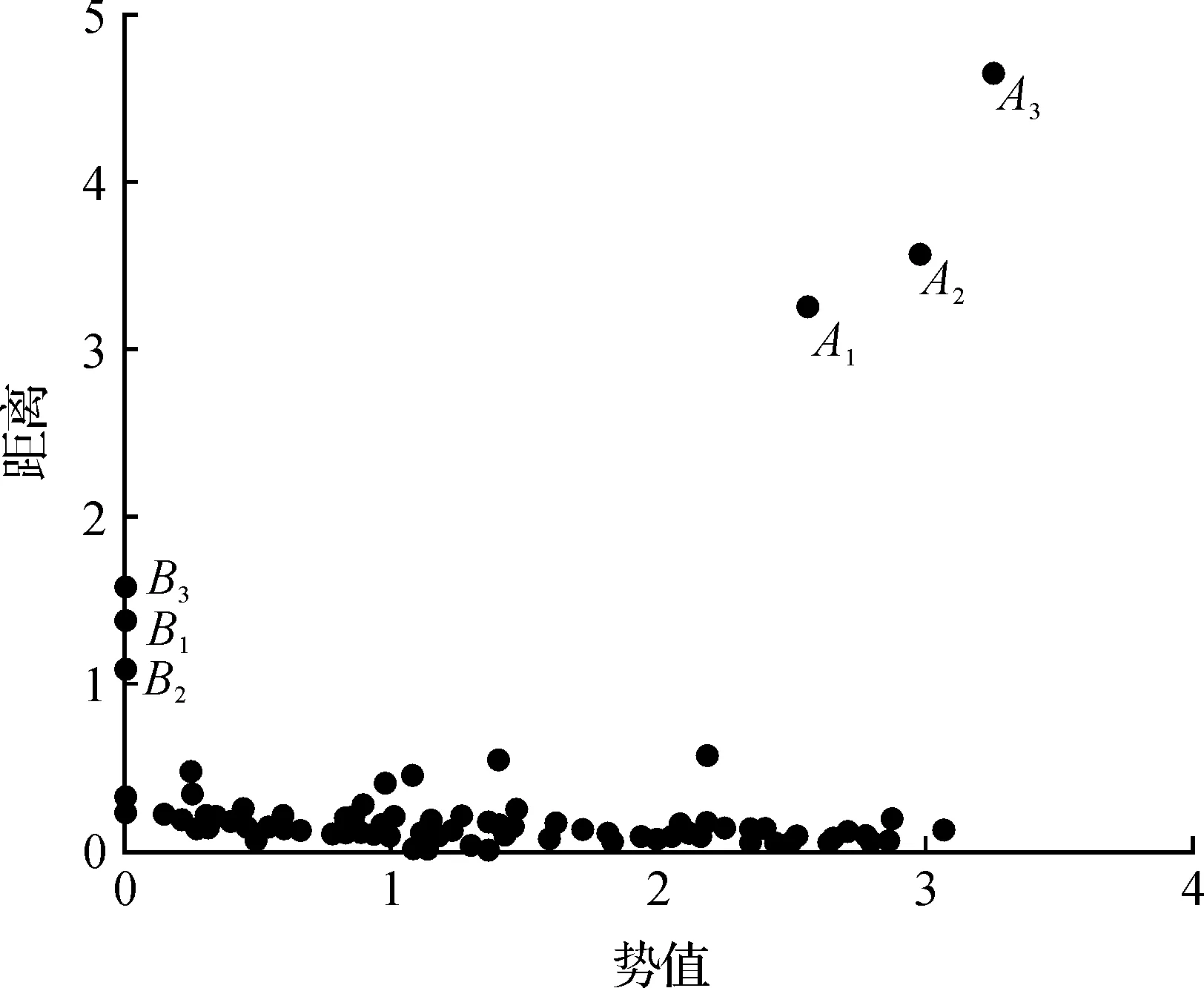
圖4　數據對象勢值和距離分布圖Fig.4　Potential value and distance distribution map of data objects

圖3中B1，B2，B3是原始數據分布中的3個簇的簇類中心，其在圖4中具有較大的勢值φ(xi)和較大的距離δi；A1，A2，A3是遠離簇的數據點，即離群點，其在圖4中具有較小的勢值φ(xi)和較大的距離δi；而其余點均屬于某個簇類，具有較小距離δi的性質.

通過分析圖4可以確定數據集的簇類中心，等簇類中心確定后，將其余點按到最近鄰的更高勢值對象的最小距離進行劃分，使得當前對象的類別標簽與高于當前對象勢值的最近鄰對象的標簽一致，從而對所有對象的類別進行標定.該過程與傳統劃分算法不同，只需一步完成，不需要迭代計算.

對于噪聲點，算法無需用人為設定噪聲點閾值截斷的方法去除噪聲點，而是先算出類別之間的邊界，然后找出邊界中勢值最高的點的勢值作為閾值，將此勢值閾值記為φb，只保留此類別中大于或等于此勢值的點.

算法在參數設定上只需要輸入影響因子σ的值，其作用在于控制對象間的相互作用力程，因此σ值的選擇也變得至關重要.淦文燕等[12,20]通過求解最小勢熵的方法確定最優影響因子取值，由于勢熵越大，則表明此時產生的數據場越不穩定；勢熵越小，則說明此時產生的數據場越穩定.因此，淦文燕等將影響因子的優化問題轉化求解最小勢熵的問題.DF_SPCA算法借鑒影響因子優化算法來確定影響因子σ的值，進而對σ值進行整定，使得算法對于不同的數據集，能夠根據勢熵最小化原則確定相應的σ值.

2.2　算法描述

輸入：數據集D={x1,x2,…,xi,…,xn}，影響因子σ的值.

輸出：聚類結果.

步驟1根據式(2，3)計算每個數據對象xi的勢值φ(xi)和相應最小距離δi.

步驟2根據每個數據對象xi的勢值φ(xi)和相應最小距離δi作出勢值和距離分布圖，分析勢值和距離分布圖確定聚類中心.

步驟3等聚類中心確定后，將所有數據對象按勢值從大到小排序.

步驟4將排序后的數據對象序列，按次序將這些點按到最近鄰的更高勢值對象的最小距離進行劃分.

步驟5聚類完成，輸出聚類結果.

3實驗與性能分析

實驗操作系統為Windows 7，開發平臺為Microsoft Visual C++ 2010.硬件條件：CPU為Intel Core I5 2.6 GHz，內存為4 GB.為了驗證新算法DF_SPCA的性能，算法對5個數據集進行測試.Aggregation，Spiral，Flam這3個數據集來自于東芬蘭大學(http://cs.joensuu.fi/sipu/datasets/),而其他2個數據集來自UCI數據庫，具體信息如表1所示.

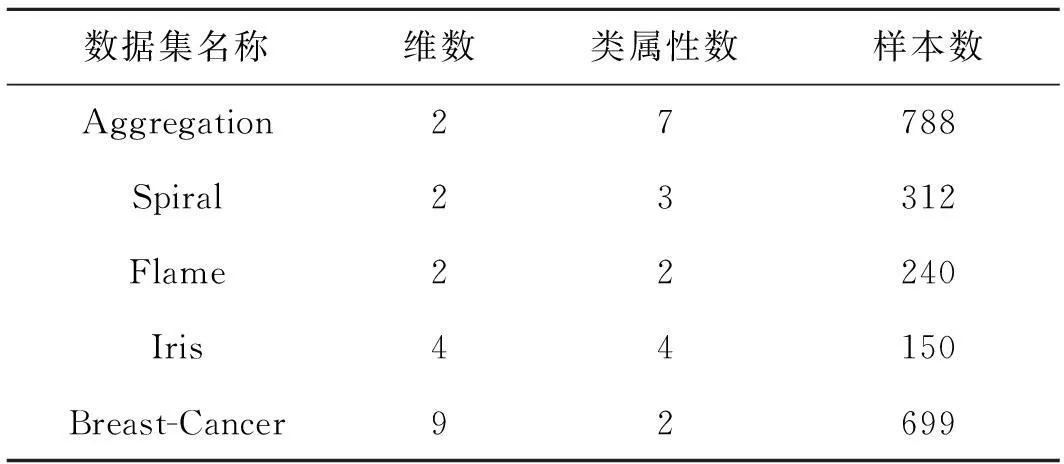
表1　5個真實數據集信息

3.1　聚類結果評價

DF_SPCA采用由Huang和Ng[21]提出的聚類準確率作為評價標準：聚類準確率r的定義為

(4)

式中：ai為最終被正確分類的樣本數目；k為聚類數；n為數據集中的樣本個數.聚類準確率越高，說明算法的聚類質量越高.當聚類準確率為1時，說明算法該數據集上獲得的聚類結果是完全正確的.

3.2　實驗結果分析

數據集Aggregation、數據集Spiral、數據集Flame均為二維數據，其中包含各種形狀的簇.算法對這3個數據集進行測試，其得到的勢值與距離分布圖和相應聚類結果展示如圖5，6所示.

圖5　3個數據集的勢值和距離分布圖Fig.5　Potential value and distance distribution map of the three data sets

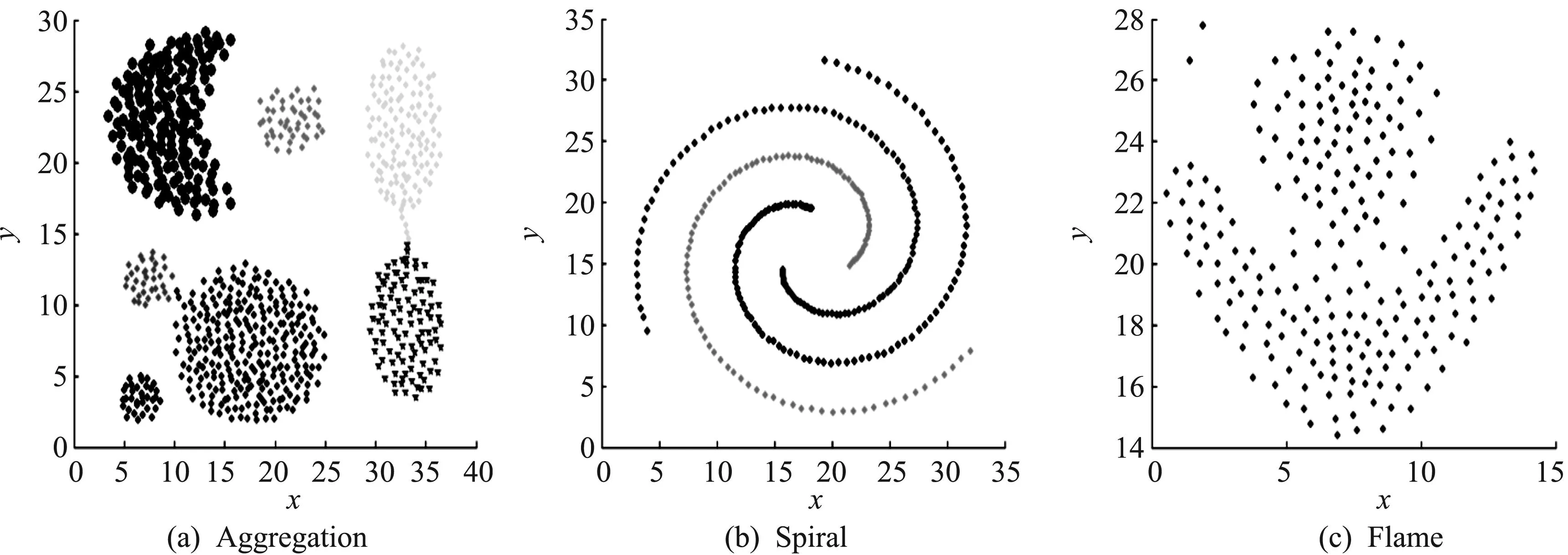
圖6　3個數據集的聚類結果分布圖Fig.6　Clustering result distribution map of the three data sets

對于數據集Aggregation、數據集Spiral、數據集Flame，算法均能夠得到聚類準確率100%的聚類結果.實驗結果表明：算法對任意形狀和變密度的簇進行聚類，均能獲得較高的聚類質量.

算法對UCI數據庫數據進行測試，首先對Iris數據進行實驗.Iris數據集包含150個數據集，每個數據對象由4個屬性值描述，數據集分為3個類：Iris-Setosa，Iris-Versicolour和Iris-Virginica.并在此說明，所有的數據集中，類屬性只用來評估算法的聚類結果，不參與聚類過程.圖7給出了算法在Iris數據上得到的勢值與距離分布圖，其對應的σ為0.213.

圖7　Iris數據的勢值與距離分布圖Fig.7　Potential value and distance distribution map of Iris data set

DF_SPCA算法、K-means算法、DBSCAN算法、DF_DBSCAN算法[18]在Iris數據集上的聚類準確率r如表2所示.

表2　4種算法在Iris數據集上的聚類準確率r

表2中的聚類結果表明：DF_SPCA算法的聚類準確率比K-means和DBSCAN分別高出了11.5%和26.67%，與DF_DBSCAN算法相當，因此DF_SPCA算法和DF_DBSCAN算法在Iris數據集上均能夠獲得較好的聚類質量.

Breast-Cancer(乳腺癌)數據集最早由Wisconsin州立醫院大學提供，含有699個數據對象，分為2個類：惡性腫瘤(Malignant)和良性腫瘤(Benign).每個數據對象由9個數值屬性描述.圖8給出了DF_SPCA算法在Breast數據上得到的勢值與距離分布圖，其對應的σ為6.824.

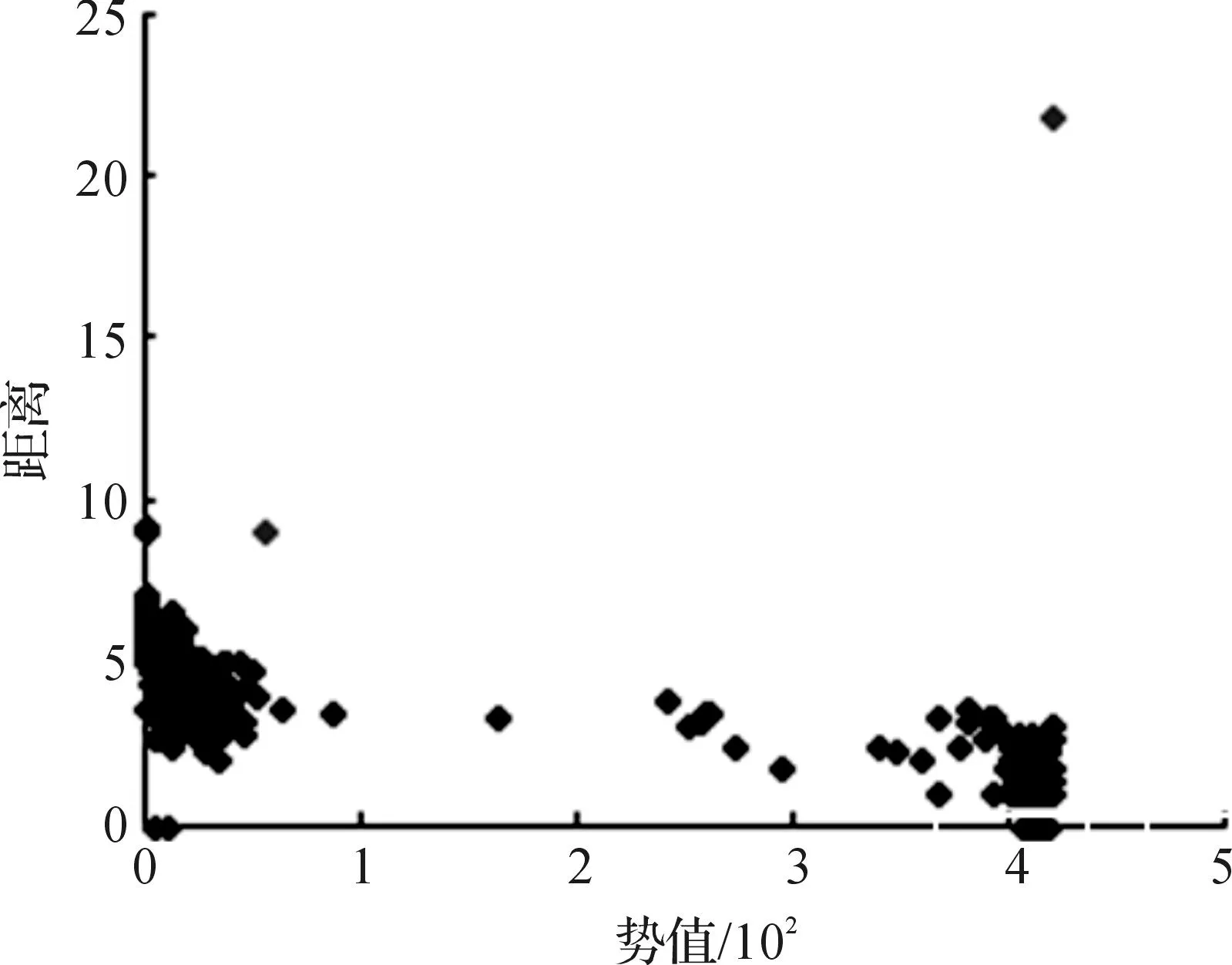
圖8　Breast數據的勢值與距離分布圖Fig.8　Potential value and distance distribution map of Breast data set

DF_SPCA算法、K-means算法、DBSCAN算法、DF_DBSCAN算法在Breast數據集上的聚類準確率r如表3所示.

表34種算法在Breast數據集上的聚類準確率r

Table 3Clustering accuracy of four algorithms on Breast data set

算法K-meansDBSCANDF_DBSCANDF_SPCAr0.92800.65520.91560.9380

表3中的聚類結果表明：DF_SPCA算法的聚類準確率比K-means、DBSCAN和DF_DBSCAN分別高出了1%，28.28%和2.24%.因此DF_SPCA算法的性能更好.

算法在不同數據集的實驗結果表明：DF_SPCA算法與其他算法相比，能夠取得更好的聚類準確率，因此算法的性能更好.

3.3　算法復雜度分析

假設聚類對象數據集規模是n個數據(樣本)，則DF_SPCA算法的時間復雜性主要由計算每個數據對象的勢值與距離構成的，該過程的計算復雜度分別為O(n2)，等聚類中心確定后，算法只需經過一次劃分就能完成聚類，其計算復雜度為O(n-k)，其中k為確定的聚類中心數目.

一般基于劃分的聚類算法，如k-means算法，其時間復雜度是O(tkn)，通常基于層次和基于密度聚類算法，如DBSCAN算法，其時間復雜度為O(n2)，其中t為迭代次數，k為聚類個數，n為數據對象個數.DF_DBSCAN算法的時間復雜度與DBSCAN算法相似.從以上理論分析可知：相比于基于劃分聚類算法，DF_SPCA算法復雜度要高，但與基于層次和基于密度的聚類算法相當，主要消耗在計算每個數據對象的勢值和距離的過程中，但是其優勢在于無需確定聚類個數，并能自動確定聚類中心和對于任意形態分布的數據集均能得到較滿意的聚類結果，因此可以在一定程度上彌補其時間復雜度較高的缺陷.

4結論

筆者提出了一種基于數據場和單次劃分的聚類算法(DF_SPCA)，引入數據場理論，使其具有反映數據間多對一作用關系的優勢，進一步計算每個數據對象的勢值和相應的距離.通過分析每個數據對象的勢值和距離分布確定簇類中心，得到的聚類結果更加符合數據的原始分布，使能獲得較好的聚類質量，實驗驗證了本算法的可行性和有效性.DF_SPCA算法的惟一參數σ值采用勢熵最優算法選取，使得算法具有一定的自適應性，同時算法不需要預先設定聚類個數，能夠自動確定聚類中心，并且能夠處理任意形狀的簇和離群點.下一步的研究重點是使用DF_SPCA算法對混合屬性數據實現高質量的聚類，進一步探討如何對混合屬性數據進行高效聚類.

參考文獻：

[1]HAN J, KAMBER M. Data mining concepts and techniques[M]. San Francisco: Morgan Kaufmann,2001.

[2]ZHANG W, YOSHIDA T, TANG X J, et al. Text clustering using frequent item sets[J]. Knowledge-based systems,2011,23(5):379-388.

[3]HAN J, KAMBER M, PEI J. Data mining concepts and techniques[M]. 3th ed. San Francisco: Elsevier,2011.

[4]IAMON N, BOONGOEN T, GARRETT S, et al. A link-based cluster ensemble approach for categorical data clustering[J]. IEEE knowledge and data engineering,2012,24(3):413-425.

[5]龍勝春，傅佳琪，堯麗君.改進型K-Means算法在腸癌病理圖像分割中的應用[J].浙江工業大學學報，2014,42(5):581-585.

[6]高雪，謝儀，候紅衛.基于多指標面板數據的改進的聚類方法及應用[J].浙江工業大學學報，2014,42(4):468-472.

[7]肖剛，吳利群，張元鳴，等.一種基于協作頻度聚類的Web服務信任評估方法[J].浙江工業大學學報，2014,42(4):393-399.

[8]淦文燕,李德毅.基于核密度估計的層次聚類算法[J].系統仿真學報,2004,16(2):302-306.

[9]余建橋,張帆.基于數據場改進的PAM聚類算法[J].計算機科學,2005,32(1):165-168.

[10]王海軍,鄧羽,王麗,等.基于數據場的C均值聚類方法研究[J].武漢大學學報(信息科學版),2009,34(5):626-629.

[11]李學,苗奪謙,馮琴榮.基于數據場的粗糙聚類算法[J].計算機科學,2009,36(2):203-206.

[12]李春芳,劉連忠,陸震.基于數據場的概率神經網絡算法[J].電子學報,2011,39(8):1739-1745.

[13]JI Z X, SUN Q S, XIA D S. A modified possibilistic fuzzy c-means clustering algorithm for bias field estimation and segmentation of brain MR image[J]. Computerized medical imaging and graphics,2011,35(5):383-397.

[14]BERGET I, MEVIK H B, NAES T. New modifications and applications of fuzzy C-means methodology[J]. Computational statistics & data analysis,2008,52(5):2403-2418.

[15]ESTER M, KRIEGEL P H, SANDER J, et al. A density-based algorithm for discovering clusters in large spatial databases with noise[C]// Proceedings of the National Conferences on Aritificial Intelligence. Stockholm: Stockholm University,1998:226-231.

[16]DAVE R N, BHASWAN K. Adaptive fuzzy c-shells clustering and detection of ellipses[J]. IEEE transactions on neural network,1992,3(5):643-662.

[17]ANKERST M, BREUNIG M, KRIEGEL H P, et al. OPTICS: ordering points to identify the clustering structure[J]. ACM sigmod record,1999,28(2):49-60.

[18]楊靜,高嘉偉,梁吉業,等.基于數據場的改進DBSCAN聚類[J].計算機科學與探索,2012,6(10):903-911.

[19]李德毅,杜鹢.不確定性人工智能[M].北京:國防工業出版社,2005.

[20]淦文燕,李德毅,王建民.一種基于數據場的層次聚類方法[J].電子學報,2006,34(2):258-262.

[21]HUANG Z. Clustering large data sets with mixed numeric and categorical values[C]// In the first Pacific-Asia Conference on Knowledge Discovery and Data Mining. Singapore: World Scientific Publishing,1997:21-34.

(責任編輯：劉巖)

A single partition clustering algorithm based on data field

ZHANG Ni, CHEN Tiantian, HE Xiongxiong

(College of Information Engineering, Zhejiang University of Technology, Hangzhou 310023, China)

Abstract:Most existed clustering algorithms have problems such as low clustering quality, parameter sensitivity, and difficulty in determining cluster centers and number of clusters. In this paper, a single partition clustering algorithm based on data field (DF_SPCA) is proposed to solve the problems. Firstly, through analyzing the distribution of the data, the data field theory is introduced. Base on analysis of each data object distance and force distribution, the cluster center is determined Then the rest data point will find out the nearestt point from the data points with higher potential value and keep in same cluster with it. Finally, the proposed method is tested on a series of data sets and the results show that DF_SPCA algorithm has a better clustering quality and can deal with clusters of arbitrary shape.

Keywords:data field; data clustering; potential value; cluster analysis; potential value and distance distribution

中圖分類號：TP39

文獻標志碼：A

文章編號：1006-4303(2016)01-0052-06

作者簡介：張霓(1970—)，女，浙江杭州人，副教授，碩士生導師，研究方向為醫療信息系統和移動機器人，E-mail:zn@zjut.edu.cn

基金項目：國家自然科學基金資助項目(61473262)

收稿日期：2015-06-19