網式過濾器的計算模型選擇及內部流場分析

陶洪飛，朱玲玲，馬英杰，滕曉靜，鄭文強

(新疆農業大學水利與土木工程學院，烏魯木齊 830052)

2010年中央1號文件《關于加快水利改革發展的決定》提出加大水利建設，實施最嚴格的水資源管理制度，在新疆農業用水占社會經濟總用水的96%，而對GDP的貢獻率卻只有17.1%，而農業灌溉僅有39.2%采用了高效節水灌溉，對于水資源短缺的新疆來說農業節水潛力還很大[1]。根據《新疆高效節水建設方案》及《新疆農業節水建設發展規劃》確定了每年完成農業高效節水面積20萬hm2以上，至2020年新疆農業高效節水面積累計達到286.667萬hm2以上的推廣目標。目前，新疆已建的有關農業高效節水工程，灌溉水源絕大部分為地下水，但許多地區的地下水超采嚴重，所以未來選擇地表水作為灌溉水源已成為新建微灌工程的最優選擇[2]。新疆河水多為山溪性河流，泥沙含量高，易造成灌水器(如滴頭、微噴頭等)堵塞，目前，采用的是沉沙池和組合式過濾器的方法去除微灌用水中的泥沙，以防止灌水器堵塞，從而保障工程的正常運行[3,4]。過濾器是微灌系統中的關鍵性設備之一，其中網式過濾器相對于砂石過濾器和疊片過濾器而言，具有容易操作、更方便清洗及對無機污染物有較高的去除效率等優勢[5]。目前，大部分學者[6-11]開展了有關網式過濾器系列產品的水力性能、去除效率及結構優化等方面的研究。WU[12]根據網式過濾器的結構參數和大量的水頭損失試驗數據，得到了一個水頭損失計算的三維模型。

通過查閱相關文獻，發現對網式過濾器內部流場的研究很少，分析原因是網式過濾器的內部結構較為復雜，很難通過現有的測試手段(如PIV或LDP)來測量速度場，但隨著計算機的廣泛應用以及計算機容量的增大，仿真模擬流動已具有很高的可靠性和準確度。故選擇正確的數學模型對網式過濾器中的流場進行數值模擬不失為一種有效的方法。因此，筆者采用Fluent軟件開展了網式過濾器過濾過程中的清水流場模擬，并將計算結果同物理試驗結果對比，從而選擇最適合模擬網式過濾器內部流場的數學模型，并在此基礎上分析了該過濾器的清水流場，計算結果為該過濾器的后續研究工作奠定了基礎，同時也為研究網式過濾器提供了一種新的研究手段。

1 網式過濾器的介紹

由圖1可知，網式過濾器由罐體、濾網、控制器等主要部分組成，其關鍵參數包括罐體長度1.031 m，直徑0.254 m；濾網長度0.961 m，直徑為0.2 m；進、出口直徑均為0.2 m；排污口直徑0.05 m。

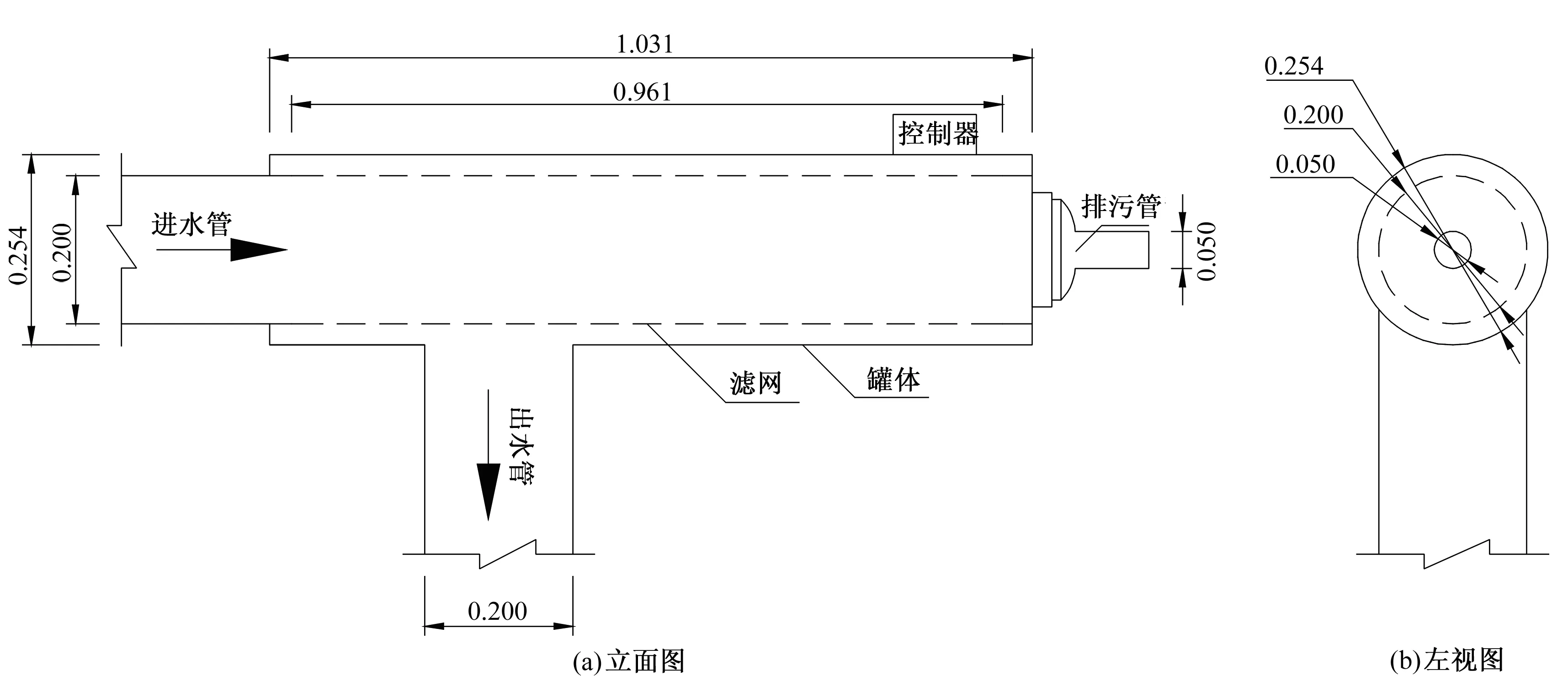
圖1 網式過濾器結構示意圖(單位：m)Fig.1 Structural diagram of screen filter

過濾器的工作原理描述如下：當灌溉水從進水管流入網式過濾器中，所有大于網孔孔徑尺寸的污物都會滯留在濾網上，而過濾水則流向出水管；隨著污物的累積，水頭損失逐漸增大，當水頭損失達到預設壓差值時，控制器自動開啟排污閥進行排污，排污的同時過濾依然進行，滿足灌溉需水要求，當達到預設的排污時間時，排污閥自動關閉，沖洗結束，繼續過濾。

2 網式過濾器的CFD模擬

2.1 數學模型

采用Fluent軟件中的多孔介質階躍(Porous Jump)模型來模擬濾網，多孔介質相關參數表達式如下：

(3)

式中：C1為阻力系數，m-2；C2為慣性損失系數，m-1；α為滲透率，m2；D為濾網孔直徑，mm；ε為孔隙比(也叫“篩分面積百分比”)，%。

根據物理試驗中采用的濾網參數：濾網孔直徑D=0.18 mm，孔隙比ε=38%，絲徑d=0.112 mm。根據給定的參數值，可計算得到：C1=3.24×1010m-2，C2=219 703.2 m-1，α=3.09×10-11m2。數值計算時考慮過濾網的厚度，其值為0.001 m。

分別選用Fluent6.3提供的Standardk-ε、RNGk-ε及Realizablek-ε為數值計算的湍流模型，與多孔介質階躍模型耦合求解。這3種模型的湍動能k和耗散率ε的方程見文獻[13]。

2.2 坐標建立

圖2為網式過濾器的三維坐標。從圖2中可知該過濾器的長度方向為X坐標，寬度方向為Z坐標，高度方向為Y坐標。為分析該網式過濾器中的流場分布情況，分別截取X=0.51 m、Y=0 m及Z=0 m 3個典型代表面進行分析研究。并定義遠離出水口一側的濾網為上濾網，靠近出水口一側的濾網為下濾網；分別選取Y=±0.114、±0.1、±0.086斷面與Z=0斷面相交的6條線：Y1=0.114(上濾網外側)、Y2=0.1(上濾網)、Y3=0.086(上濾網內側)、Y4=-0.086(下濾網內側)、Y5=-0.1(下濾網)、Y6=-0.114(下濾網外側)來分析濾網及其內、外側的流速。

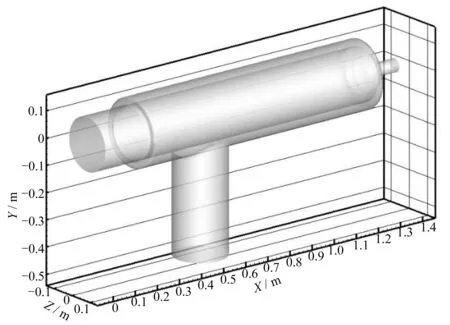
圖2 三維坐標Fig.2 Three-dimensional coordinate

2.3 網格劃分及計算方法

為減少數值模擬的計算工作量和保證計算精度，對過濾器的計算網格進行了優化。將過濾器的網格進行分塊劃分，進、出口因為結構簡單，采用六面體結構性網格，其余部分采用四面體非結構網格，網格總數為123 252個。

對網式過濾器的數值計算采用非定常的壓力基隱式算法，研究的計算區域和控制方程的離散均采用有限體積法。采用Fluent6.3提供的SIMPLE算法來計算壓力與速度的耦合方程，差分格式采用精度更高的二階迎風格式。殘差標準為1.0×10-3，迭代時間步長為0.000 1 s。

2.4 邊界條件

(1)過濾器進水管中運動的水流，可近似視為均勻流，取進流方向與X軸正向一致，故設置進水口的邊界條件為速度進口：U=u，V=0，W=0。根據網式過濾器物理模型試驗情況，進流量為352.1 m3/h，則根據流速定義可得該工況下u= 3.11 m/s。

(2)網式過濾器出水口的邊界條件設置成壓力出口，壓力大小為200 kPa。

(3)網式過濾器的罐體、管道內壁及排污管均按固壁定律進行處理，采用無滑移邊界條件，即U=V=W=0。

3 最優數學模型的確定

3.1 水頭損失對比

對于過濾器而言，我們最為關注的是其水頭損失，因為其值的大小是評價過濾器性能的一個重要標準。表1為物理試驗結果與數值模擬結果的水頭損失對比情況，從表1中可知，物理試驗中網式過濾器的水頭損失為3 m，而紊流模型中的Standardk-ε模型、RNGk-ε模型、Realizablek-ε模型的計算水頭損失分別為3.91、3.18、3.12 m，與物理試驗結果的相對誤差分別為30.3%、6.0%、4.0%，因此，Realizablek-ε模型與多孔介質階躍模型耦合的計算結果同物理試驗結果吻合最好。同時也驗證了Realizablek-ε模型可以模擬高應變率及彎曲程度較大的流動[14,15]。

表1 結果對比Tab.1 Results comparison

3.2 計算耗時對比

網式過濾器的數值計算是在同一臺計算機上進行，計算機內存都占用127 MB，CPU都占用25%，而當進、出口流量平衡，即完全收斂時，從表2可知，RNGk-ε模型計算用時272 min> Standardk-ε模型計算用時271 min> Realizablek-ε模型計算用時269 mim，但總的來說，三者計算時間相差不大，最長與最短的計算相差僅為3 min。

表2 3種模型的計算時間對比Tab.2 Time comparison of three models

通過水頭損失和計算耗時對比，最終選擇Realizablek-ε模型與多孔介質階躍模型來模擬網式過濾中的流場。

4 流場分析與討論

4.1 速度場對比

圖3為網式過濾器中不同斷面的速度矢量分布圖。從圖3(b)和圖3(c)中可知，水流從進水管處均勻地流入網式過濾器中，當水流進入罐體時，水流的速度分布特性發生改變，一部分水流進入上濾網，通過濾網孔進行過濾；一部分水流進入下濾網進行過濾，當突然遇到出水口邊界時，流速分布發生了巨大的變化，水流由沿X軸正向運動快速轉變為沿出水管右側斜向下運動，從而造成出水管左側的部分區域產生漩渦，水流運行33 cm左右的距離后，水流沿出水管均勻地向下運動；而X=0.61 m處以后的水流速度大部分呈“點狀”分布，說明流速很小。從圖3(a)中可知水流在出水管中的流速是關于Z=0截面對稱分布的，靠近管壁內側的水流流速較大，在運動至距出水口10 cm處時，水流流速會減小。

圖3 不同斷面的速度矢量圖Fig.3 Velocity vector diagram of the different section

圖4為網式過濾器中不同斷面的速度云圖。從圖4(b)和圖4(c)中可以看出進水管中的水流流速分布比較均勻，為3.0 m/s左右；當水流運動至罐體時，過水斷面面積增大，水流流速減小，水流繼續運動一段路程，過水斷面面積沒變，但流速卻沿X方向逐漸減小，最終達到一個恒定值為0.5 m/s左右。這是因為受到排污口固體邊界條件的影響，當水流運動至該處時，水流會發生反向流動，與沿X軸正向運動的水流發生碰撞、摩擦和混摻，從而消耗大量的能量，造成水流流速減小。由于出水口邊界條件影響，出水口中間處的水流流速依然較大，為5.0 m/s左右，而左、右側漩渦處的流速較小，為0.5 m/s左右。從圖4(a)可知出水管中的水流流速關于Z=0斷面對稱分布，水流在出水管Y=-0.12 m左右時的流速最大，5.0 m/s左右。

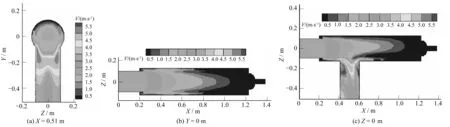
圖4 不同斷面的速度云圖Fig.4 Velocity contours diagram of the different section

4.2 壓強場對比

圖5為網式過濾器中不同斷面的壓強場。從圖5(a)可知出水口正上方罐體中的水流壓強由中心向四周逐漸減小，與速度流場分布規律相反，中心處壓強最大，可達230 kPa左右，濾網附近最小的壓強為210 kPa左右，兩者相差約20 kPa。從圖5(b)可知，X=0～0.2 m處，壓強分布比較均勻，X=0.2～0.75 m處，上、下濾網的內外壓差較大，這是因為水流進入罐體后會以一個相對較大的流速分別流向上、下濾網，并經過濾網孔完成過濾，從而造成濾網的內外壓差；X>0.75 m，上、下濾網的內外壓差較小，壓強分布較均勻。從圖5(c)可知進水管處的水流壓強明顯大于出水管處的水流壓強。由于受到罐體中上、下濾網及出水口邊界條件的影響，水流從進水管流至出水管過程中會發生局部水頭損失和沿程水頭損失。故當位置水頭和流速水頭一定時，進水管處的壓強大于出水管處的水流壓強，與實際液體恒定總流的能量方程相符合。

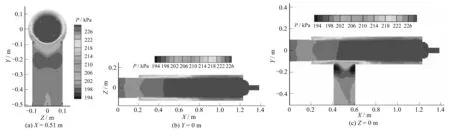
圖5 不同斷面的壓強場Fig.5 Pressure flow of the different section

5 流速討論

圖6為水流流速沿X軸的變化曲線。從圖6(a)中可得出2點：①上濾網及上濾網外側的水流流速沿X軸的變化包含兩個階段：流速迅速增大階段。X=0.2～0.25 m時，上濾網及上濾網外側的水流流速沿X軸迅速增加，但上濾網的水流流速增加幅度明顯大于上濾網外側，上濾網的流速最大值達2.2 m/s左右，約為上濾網外側流速最大值的兩倍。流速逐漸減小階段。X=0.25～1.23 m時，上濾網及上濾網外側的水流流速逐漸減小，雖然減小幅度不同，但減小趨勢大體相同。②上側濾網內側的水流流速沿著X軸逐漸減小，且水流流速比上濾網外側的水流流速大很多，但兩者的流速差卻沿著X軸逐漸減小，兩者的最大流速差約為2 m/s；當X=1.05～1.191 m時，上濾網內、外側的水流流速大體相同，流速差幾乎為0。從圖6(b)中可知，下濾網及其內外側的水流流速沿X軸方向的變化規律，與上濾網及其內外側的有所不同，主要是因為出水口邊界條件的影響。

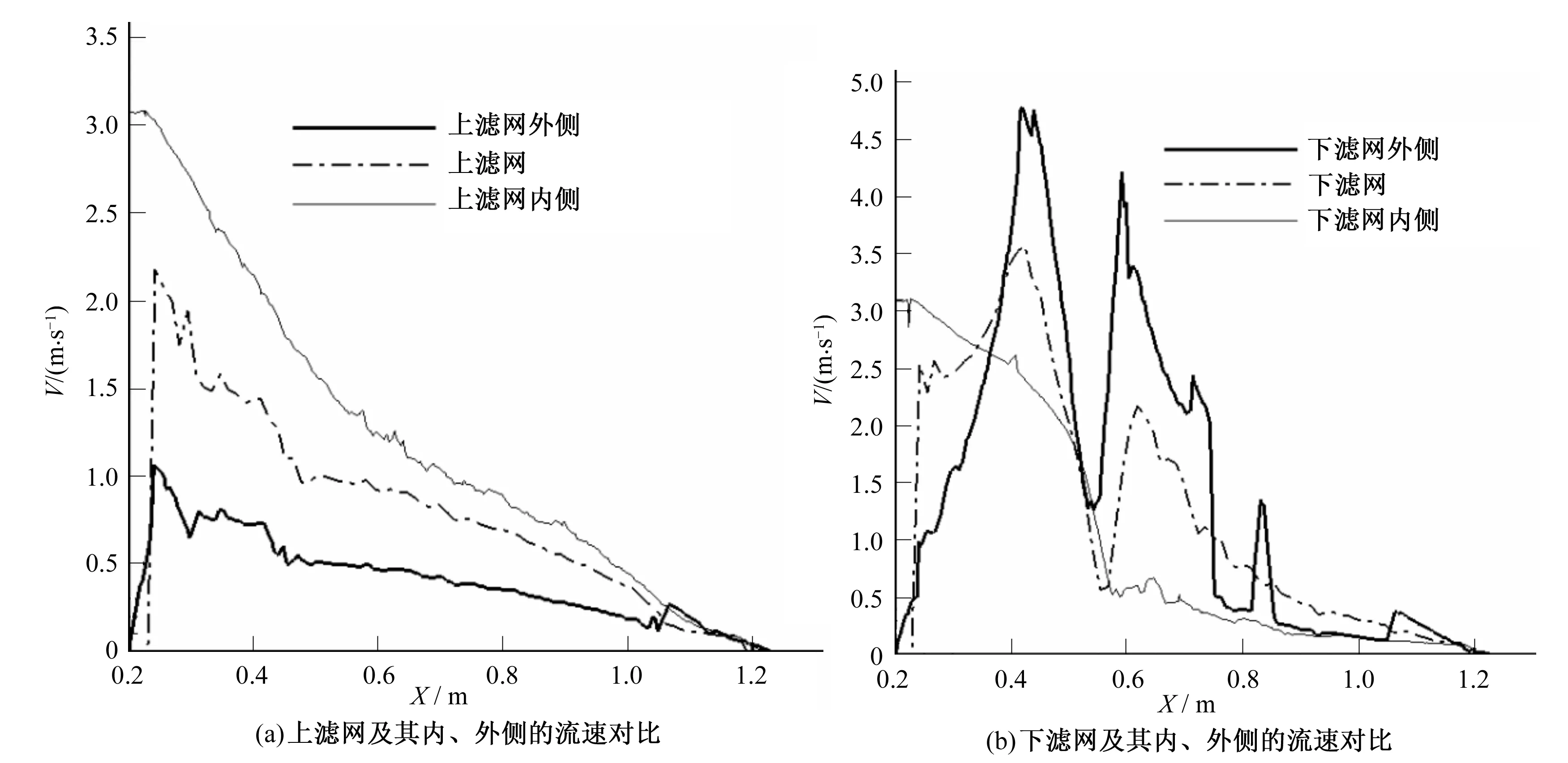
圖6 水流流速沿X軸的變化曲線Fig.6 Change curve of water velocity along X axis

綜上所述，濾網內、外側的水流流速沿X軸方向的分布很不均勻，從而影響網式過濾器的過濾效率，特別是網式過濾器尾部附近的濾網，內、外側流速相差較小，水的滲透率就較小，導致過濾效率較低，如何提高網式過濾器的過濾效率值得進一步研究，可通過改變出水管出水口位置解決水流流速分布不均勻的問題。

6 結 語

利用Fluent6.3軟件對網式過濾器的內部流場進行數值模擬，主要得到以下結論。

(1)Realizablek-ε模型與多孔介質階躍模型能更好地模擬該網式過濾器的內部流場，這為今后該過濾器的結構優化、沖洗過程及水沙兩相流流場的數值模擬奠定了基礎。

(2)得到了水流從進水管進入網式過濾器并流出出水管的運動狀態，指出排污口固體邊界和出水口邊界條件對該過濾器的速度流場和壓強場分布規律影響很大。

(3)濾網內外側的水流流速沿X軸的分布不均勻，但由于出水口固壁邊界條件條件的影響，上濾網水流的流速沿X軸的分布規律不同于下濾網，降低了網式過濾器的過濾效率；同時濾網內外側較大的壓強差，容易導致濾網變形，直至損壞，故減小流速和壓強的不均勻分布有待進一步研究。

[1] 蘇 薈.新疆農業高效節水灌溉技術選擇研究[D]. 新疆石河子：石河子大學，2013.

[2] 孫 娟.河水滴灌重力沉沙過濾池的設計與應用推廣[J].節水灌溉，2014,(1):60-64.

[3] 陶洪飛，邱秀云，李 巧，等.不同鰓片間距下的分離鰓內部流場三維數值模擬[J].農業機械學報，2014，45(6):183-189.

[4] 陶洪飛，邱秀云，趙麗娜，等.水沙分離鰓內部流場的數值模擬[J].農業工程學報，2013，29(17)：38-46.

[5] Tajrishy MA,Hills DJ, Tchobanoglous G. Pretreatment of secondary effluent for drip irrigation[J]. Journal of Irrigation and Drainage,1994,120(4): 716-731.

[6] 劉煥芳，劉 飛，谷趁趁，等.自清洗網式過濾器水力性能試驗[J]. 排灌機械工程學報，2012，(2)：203-208.

[7] Avner Adin, Giora Alon. Mechanisms and process parameters of filter screens[J]. Irrigation and Drainage Engineering, 1996,293(4):112-115.

[8] Thokal R T, Raghavendra A G, Suresh N M, et al. Effect of sand particle size and concentration on performance of screen filter in trickle irrigation[J]. An-nals of Arid Zone, 2004,43(1):65-71.

[9] 宗全利，劉 飛，劉煥芳，等.滴灌用自清洗網式過濾器排污壓差計算方法[J].農業機械學報，2012，43(11)：107-112.

[10] 劉煥芳，鄭鐵剛，劉 飛，等．自吸網式過濾器過濾時間與自清洗時間變化規律分析[J]．農業機械學報，2010，41(7)：80-83.

[11] 劉 飛，劉煥芳，宗全利，等.自清洗網式過濾器水頭損失和排污時間研究[J].農業機械報，2013，44(5)：127-134.

[12] Wenyong WU, Wei CHEN, Honglu LIU, et al. A new model for head loss assessment of screen filters developed with dimensional analysis in drip irrigation systems [J]. Irrigation and Drainage, 2014 (63):523-531.

[13] 白兆亮，李 琳. 有壓管道中孔板相對間距對局部阻力系數的影響及其機理研究[J].水電能源科學，2015，33(1)：177-182.

[14] 于 勇. FLUENT入門與進階教程[M].北京：北京理工大學出版社，2010.

[15] 江 帆，黃 鵬. FLUENT高級應用與實例分析[M].北京：清華大學出版社，2010.