灌區多水庫聯合優化調度研究

吳 振，顧文權 ，邵東國

(武漢大學 水資源與水電工程科學國家重點實驗室，武漢 430072)

水資源時空分布極度不均衡造成的資源型缺水問題已嚴重制約了區域經濟的發展。在資源型缺水區，單庫調度通常難以滿足自身灌區用水需求，多水庫聯合調度能在更大尺度上綜合考慮水資源的調配，將水資源豐富區域的水調到水資源緊缺的區域，為緩解缺水地區水資源危機提供了一種重要手段[1]。科學有效的調水規則和供水規則是指導多水庫有效調水和供水的關鍵。為此，國內外學者對多水庫聯合運用規則做了大量理論與方法方面的探索[2-7]。郭旭寧、胡鐵松[8]等提出了基于集對分析的水庫群聯合調度規則研究以及確定水庫調水和供水規則的二次規劃模型；I.Nalbantis等[2]建立線性模型確定各調度時段每個水庫的供水任務；王國利等[9]提出了基于協商對策的多目標群決策模型；方紅遠等[10]建立了基于供水可靠性最大、供水破壞能力最強以及單一時段破壞深度最小的多目標混合整數規劃模型。

相對單庫調度而言，多水庫聯合供水系統增加了水庫間的調水量，在實際操作中則需要增加調水規則來指導水庫調度。調水時機和調水規模是決定調水規則的關鍵因素，這兩個方面的合理確定則依賴于供水系統的目標，即不同的供水目標會生成不同的調水規則。對缺水區域而言，如何合理分配有限的水資源，減少缺水損失系統風險是人們普遍關注的熱點問題。為此，本文從風險最優化的角度建立多水庫聯合模擬優化調度模型。同時優化確定調水規則、供水規則以及調水規模，最終依據優化結果計算出各水庫區用水戶供水量，并應用于高關-短港水庫的實際調度。

1 模型介紹

1.1 目標函數

基于供水系統全局缺水風險最小化的多水庫聯合模擬優化調度模型，是將缺水風險納入目標函數中，目標函數包括缺水風險最低、棄水量最小、調水時段數最小，目標函數如下式：

(1)

式中：決策變量x,y,z分別為各水庫調水控制線、供水限制線、和調水水庫的最大調水規模；T為總時段數；Rt為缺水時段；SUi為i水庫的棄水量；N為水庫的個數；wE，WSU和WT分別為各子目標的權重。

1.2 約束條件

(1)水量平衡約束：

Vt+1=Vt+It-Qt-Lt-SUt-Dt

(2)

式中：Vt+1為t時段末蓄水量；Vt為t時段初蓄水量；It為t時段徑流量；Qt為t時段供水量；為t時段蒸發滲漏損失量；SUt為t時段棄水量；Dt為t時段調水量。

(2)水庫蓄水能力上下限約束：

Vmin≤Vt≤Vmax

(3)

式中：Vmin，Vmax分別為水庫蓄水能力的上下限。

(3)決策變量上下限約束：

Vmin≤xi,yi,zi≤Vmax

(4)

(4)水庫庫容-面積-水位特征曲線：

Zi,t=f(Vi,t),Vi,t=f(Si,t)

(5)

式中：f(Vi,t)為水位-庫容曲線函數；f(Si,t)為庫容-面積曲線函數。

為這款腕表提供動力的是精工機心8L55：37鉆，36,000vph的高頻自動機心。它擁有55小時動力儲備，以及停秒功能。SLA025在全球范圍內限量1500只，并采用“華夫餅干”格飾的黑色橡膠表帶搭配針扣。

(5)限制供水能力不超過允許破壞深度：

α1=0.9，α2=0.80

式中：α1為工業生活的供水限制系數；α2農業供水限制系數。

(6)非負約束：模型中所有變量均為非負。

1.3 缺水風險指標

(1)缺水風險的計算式子如下：

(6)

式中：Rt為缺水時段；T為供水系統總時段數；SN表示供水系統缺水總時段數。

缺水指數綜合考慮了各缺水年發生的頻率和缺水量。

(2)平均易損性是用來刻畫供水破壞造成后果的嚴重程度，本文采用平均缺水率表示易損性，計算式子如下：

(7)

1.4 模型求解

基本粒子群算法在運行過程中，很容易陷入局部最優解[11]，為避免出現局部最解，出現早熟收斂的現象，采用并行多種群混合進化的粒子群算法(PMSE-PSO)。PMSE-PSO法的具體步驟如下：①算法在可行域范圍內隨機產生M×N個粒子，其中M為子群體個數，N為每個子群體中粒子的個數，并計算每個粒子的目標函數值；②將粒子按目標函數值從小到大的順序進行排序；③按照分配規則將總群體分成M個子群體，每個子群體中粒子的個數為N；④利用 PSO算法進化每個子群體；⑤經過一定迭代次數后，將子群體進行混合，使所有粒子進行信息交流，并將每個粒子按目標函數值重新進行排序；⑥如果滿足終止準則則退出；否則回到步驟③。

2 實例應用

2.1 研究區概況

高關水庫灌區位于湖北省京山縣以北大富水流域，高關水庫灌區內有1座大型水庫、1座中型水庫、58座小型水庫以及13 893處塘堰作為灌溉水源，設計灌溉面積2.56萬hm2。其中高關水庫是灌區的骨干調節水庫，它位于湖北省京山縣北部的大富水河上游，是漢北水利總體建設規劃中的一座以灌溉為主，兼有防洪、發電、養殖等綜合效益的大(Ⅱ)型水庫，水庫控制面積303 km2，總庫容20 108萬m3，興利庫容15 432萬m3，補水至大富水及漁子河水庫。

短港水庫位于應城北部楊河鎮境內，是一座中型水庫，最大蓄水面積1 023 hm2，最大水深16 m。短港水庫攔截大富水，承雨面積70 km2，總庫容6 967萬m3，興利庫容4 141萬m3，水庫的主要功能是灌溉供水，設計灌溉面積0.8萬hm2，有效灌溉面積0.47萬hm2。

2.2 模型求解與結果分析

為緩解水資源緊缺、提高生活及工業用水保證率，充分利用高關水庫與短港水庫之間的庫容差異以及水文差異，在滿足自身需水的情況下，高關水庫向短港水庫調水，使供水系統缺水風險最低。本文選取1973-2013年的長系列資料，以2013年為現狀水平年，以月為計算時段，運用上述模型優化求解短港水庫和高關水庫調水規則，計算各水庫的供水量、缺水量，以及相關計算參數(wE為0.35，wSU為0.42和wT為0.23)，進而得到缺水風險和平均易損性(見表1和表2)，并與單庫調度結果對比分析。

從表中結果分析，單庫調度時短港水庫灌區的生活用水5%缺水損失程度的缺水風險為0.271 4，P=10%缺水損失程度的缺水風險為0.261 2，P=20%缺水損失程度的缺水風險為0.246 9，雖然缺水風險比較低，但是并沒有滿足生活供水保證率要求(90%)，而在雙庫聯調中，短港水庫的P=5%缺水損失程度的缺水風險為0.059 2，P=10%缺水損失程度的缺水風險為0.057 1，P=20%缺水損失程度的缺水風險為0.055 1，生活供水保證率達到95%左右，而且生活用水的平均缺水率(平均易損性)為0.081 3。這說明在高關水庫灌區基本保證自身供水的條件下，向短港水庫調水大大降低了短港水庫灌區的生活供水的缺水風險，充分利用了系統水資源。高關灌區水資源充足，各部門用水的滿足程度很高，缺水風險很低。其工業和生活供水的保證率達到90%左右，農業供水保證率為85%左右。向短港水庫供水后，僅對工業和農業供水產生了一些影響，工業缺水風險僅升高了1%左右，農業風險升高了30%。雖然高關水庫經兩庫聯調后的平均易損性較單庫時有所升高(生活供水從單庫供水的0升為0.039 8，工業供水從單庫供水的0.040 6升為0.079 8，農業供水從單庫供水的0.125 7降為0.240 8)，但對供水保證率的影響卻不大，卻大大降低了供水系統全局平均易損性，這是運用該模型使高關水庫對短港水庫進行了水量補償。

表1 各用水部門缺水風險Tab.1 Water shortage risk of various water use sectors

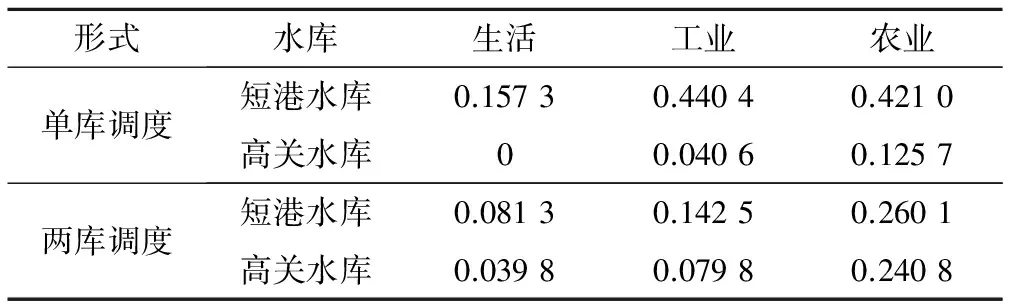
表2 各用水部門平均易損性Tab.2 Average vulnerability of various water use sectors

單庫調度時短港水庫灌區的工業用水P=5%缺水損失程度的缺水風險為0.551 0，P=10%缺水損失程度的缺水風險為0.542 9，P=20%缺水損失程度的缺水風險為0.528 6，并且平均缺水率為0.440 4，發生5%至20%缺水損失程度的概率只有2.24%，這表明極端的缺水損失比較嚴重，集中破壞大，不利于當地經濟的可持續發展。經高關水庫調水后，P=5%缺水損失程度的缺水風險為0.893 9，P=10%缺水損失程度的缺水風險為0.138 8，P=20%缺水損失程度的缺水風險為0.134 7，并且平均缺水率為0.142 5，發生5%至20%缺水損失程度的概率為75.92%，意味著避免了工業用水極端的缺水損失。單庫調度時短港水庫灌區的農業用水P=10%缺水損失程度的缺水風險為0.459 2，P=20%缺水損失程度的缺水風險為0.455 1，P=30%缺水損失程度的缺水風險為0.453 1，并且平均缺水率為0.421 0，發生10%至30%缺水損失程度的概率只有0.61%，這表明極端的缺水損失比較嚴重，集中破壞大，不利于當地農業的可持續發展。經高關水庫調水后，P=10%缺水損失程度的缺水風險為0.553 1，P=20%缺水損失程度的缺水風險為0.553 1，P=30%缺水損失程度的缺水風險為0.163 3，并且平均缺水率為0.260 1，發生5%至20%缺水損失程度的概率為38.98%，表明極端缺水損失程度明顯降低。

3 結 語

(1)在高關水庫灌區基本保證自身供水的條件下，向短港水庫調水大大降低了短港水庫灌區的生活供水的缺水風險，生活供水達到了供水保證率要求，并且避免了工業用水極端的缺水損失造成的集中破壞。而高關水庫灌區的缺水風險沒有明顯升高，因此供水系統全局缺水風險最優，充分利用了水資源，保證了兩個灌區的可持續發展。

(2)經高關水庫向短港水庫調水后，短港灌區的各用水部門的平均易損性明顯降低，雖然高關水庫灌區各用水部門的平均易損性略有升高，但并沒有影響本灌區的供水保證率，充分發揮了水庫興利效益，緩解了短港灌區的水資源短缺矛盾。

(3)本文建立的模型具有普遍意義，可以推廣到多個并聯水庫向一個水庫調水，從供水系統全局缺水風險最低的角度，同時優化確定調水規則、供水規則及最大調水規模，在調水量未知的情況下，優化調度模型，把調水水庫最大調水規模為決策變量之一，然后把優化得到的最大調水規模作為本流域最后一個虛擬的用水戶進行供水，進而確定各時段實際調水量和用水戶供水量。

□

[1] 王 強,周惠成,梁國華,等.渾太流域水庫群聯合供水調度模型研究[J].水力發電學報,2014,(3):42-54.

[2] NalbantisI,Koutsoyiannis D.A parametric rule for planning and management of multiple-reservoir systems[J].Water Resource Research,1997,33(9):2 165-2 177.

[3] Yeh WWG.Reservoir management and operations models: A state-of-the-art review [J]. Water Resources Research,1985,21(12):1 797-1 818.

[4] 劉本希,廖勝利,程春田,等.庫群長期優化調度的多核并行禁忌遺傳算法[J].水利學報，2012,43(11):1 279-1 286.

[5] 彭安幫.跨流域水庫群引水與供水聯合優化調度研究[D].遼寧大連：大連理工大學,2015.

[6] 張皓天.受水區供水水庫(群)優化調度方法研究及應用[D].遼寧大連：大連理工大學,2013.

[7] 劉 娜.跨流域水庫群聯合優化調度應用研究[D].遼寧大連：大連理工大學,2015.

[8] 郭旭寧,胡鐵松,呂一兵,等.跨流域供水水庫群聯合調度規則研究[J].水利學報,2012,(7):757-766.

[9] 王國利,梁國華,曹小磊,等.基于協商對策的群決策模型及其在跨流域調水方案優選中的應用[J].水利學報,2010,41(5):624-629.

[10] 方紅遠,甘升偉,花金祥.干旱期水庫供水風險分析的多目標規劃法[J].水力發電學報，2007,26(2):14-18,26.

[11] 曾 祥,胡鐵松,郭旭寧,等.跨流域供水水庫群調水啟動標準研究[J].水利學報,2013,(3):253-261.