調速器參數對水電站水力干擾過渡過程的影響

賴 旭，陳 強

(武漢大學 水資源與水電工程科學國家重點實驗室，武漢 430072)

0 引 言

對于采用一洞多機布置形式的電站，由于機組運行時存在水力聯系，當其中一臺機組丟棄全負荷或者大幅度增加負荷時，必然對其他正常運行的機組產生影響，這種水力干擾[1-3]引起的過渡過程將直接影響電站的供電質量，嚴重時還將影響電站的安全穩定運行。因此，針對水電站水力干擾過渡過程的研究是十分必要的。而已有水力干擾過渡過程的研究多采用簡化模型，發電機數學模型多采用簡化的一階模型，管道模型多采用彈性管道模型；只考慮引水發電管道系統和水輪機的影響，忽略了電氣系統的影響。如文獻[4]采用彈性管道模型及一階發電機模型，研究了分叉管的位置和調壓室面積等引水道參數對水電站水力干擾過渡過程的影響；文獻[5]采用一階發電機模型，研究了引水發電系統穩定以及調速器參數對系統穩定性的影響。以往調速器參數對電站過渡過程影響的研究多針對單管單機布置形式的電站，如文獻[6,7]均在單管單機仿真模型的基礎上，研究了調速器參數對單管單機水電站的小波動過程的影響。目前，針對一洞多機電站展開調速器參數對水力干擾過渡過程影響與參數優化的研究還很少。

本文采用特征線法建立管道模型及分岔管模型，并引入高階發電機模型以及勵磁系統和負載模型，建立了完整的水機電聯合仿真模型，在此基礎上研究了調速器參數對一洞多機布置形式的電站水力干擾過渡過程的影響，并利用多目標粒子群(MOPSO)算法對調速器參數進行了優化。

1 引水發電系統數學模型

水電站引水發電系統模型包括引水管道、水輪機、調速器、發電機、勵磁系統和負載，它們之間的整體關系如圖1所示。引水管道采用特征線法[8]，水輪機采用水輪機的模型綜合特性曲線[9]。

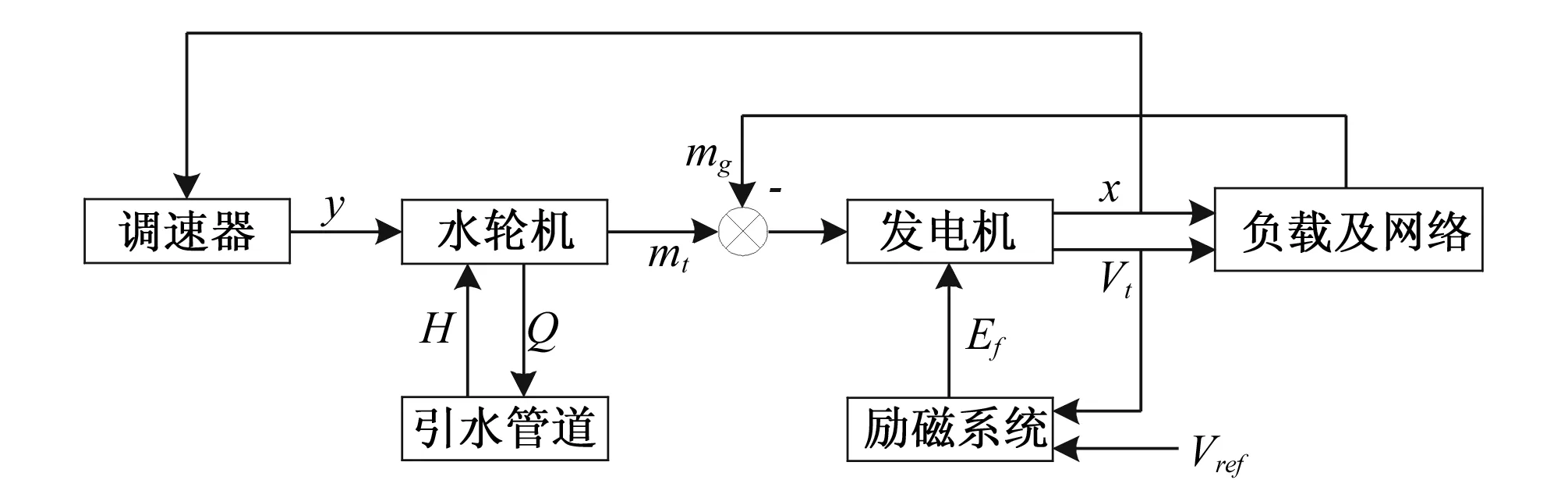
圖1 水電站引水發電系統結構框圖Fig.1 Structure of water diversion and power generation system in hydropower station

1.1 分岔管數學模型

對于如圖2所示的分岔結點，方程組可寫為[8]：

特征方程：

HA=CAP-BAQA

HB=CBM-BBQB

(1)

HC=CCM-BCQC

連續性方程：

QA=QB+QC

(2)

如果結點處的水頭損失以及不同管道的流速頭之差可以忽略，于是能量方程：

HA=HB=HC

(3)

聯立求解式(3)至式(5)，可得：

(4)

于是，HB和HC可由式(3)確定；QA,QB和QC可由式(1)確定。

對于超過三根分岔管的分岔結點，也能得出相似的方程組。

1.2 調速器數學模型

頻率調節:采用輔助接力器型調速器, 方框圖如圖3所示，其微分方程的表達式為[9]：

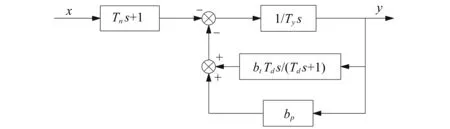
圖3 輔助接力器型調速器方框圖Fig.3 Block diagram of auxiliary Servomoter governor

(5)

功率調節，采用 PI 型控制模式，方框圖如圖4所示，其微分方程的表達式為：

圖4 PI型控制模式方框圖Fig.4 Block diagram of PI control mode

(6)

式中：x為機組轉速偏差相對值；Pg為機組給定功率；Pt為機組實際功率；Tn為測頻微分時間常數或加速時間常數；Td為緩沖時間常數；bt為暫態轉差系數；bp為永態轉差系數；Ty為主接力器時間常數。

1.3 發電機數學模型

在忽略定子繞組暫態，并忽略阻尼繞組的作用，只計及勵磁繞組的暫態和轉子動態的假設下，將轉子運動方程、電流電壓方程和電磁暫態過程方程聯合起來得到發電機三階數學模型[10,11]：

電磁暫態方程和定子磁鏈方程：

(7)

電磁轉矩方程和定子電壓方程：

(8)

轉子運動方程：

(9)

式中：ω、δ分別為轉子角速度相對值和轉子電角度；ω0為轉子額定角速度；Vt、I分別為發電機端電壓和定子電流，下標d、q分別表示d、q軸分量；Ef為由勵磁電壓所決定的假想空載電勢；E′q為發電機q軸暫態電勢；Ta為機組慣性時間常數；T′d0為d軸暫態開路時間常數；X′d為d軸暫態電抗；Xd、Xq為發電機d、q軸同步電抗；ψd、ψq為d、q軸磁鏈；Me為電磁力矩；D為阻尼系數。

1.4 勵磁系統模型

本文采用如圖5所示的I型靜止勵磁系統。

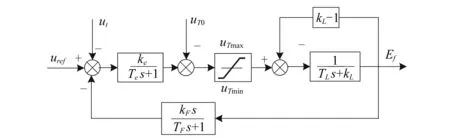
圖5 勵磁系統模型框圖Fig.5 Block diagram of excitation system model

圖5中，ke和Te分別為該慣性環節即調節器總體的放大倍數和時間常數，kL和TL分別為勵磁機的自并激常數和等值時間常數，kF和TF分別為該環節額定放大倍數和時間常數。

1.5 網絡數學模型

網絡元件主要包括輸電線路，本文采用電力系統分析中常用的輸電線路集中參數元件模型中的∏型等值電路。在電力系統穩定分析中，電力網絡一般采用穩態方程來代表。同時，假定正常運行時三相是對稱平衡的，故可以用單相系統來表示。

設線路阻抗(包括輸電線路和變壓器)為Z=Re+jXe，則有：

ΔV=IZ

若用d-q坐標系表示，則得到：

(10)

式中：i表示送端節點；j表示受端節點。

對于無窮大電網，設電網電壓為Us,則：

(11)

1.6 負荷數學模型

本文采用恒定阻抗法，即根據正常運行方式下負荷點的電壓VH0和功率SH0=PH0+jQH0,用下式求出負荷的阻抗值：

(12)

并假定暫態過程中該阻抗值不變。

2 算例分析

由以上給出的引水發電系統各環節的數學模型，按照水電機組控制系統各個環節的連接關系進行連接，建立包含水力、機械和電氣各子系統的水電站水機電聯合仿真計算模型。

如圖6所示，某電站布置形式為一洞兩機，具體參數如下：水輪機：nr=428.6 r/min，Pr=45.36 MW，Qr=31.48 m3/s，Hr=154.3 m；

引水管道：L=850 m，A=25.13 m2，l1=l2=50 m，A1=A2=12.56 m2，a=1 000 m/s；

發電機：Xd=1.07 pu，X′d=0.38 pu，Xq=0.66 pu，T′d0=5.4 s，cosφ=0.8，Ta=9.098 s，en=0，un=10.5 kV。

勵磁系統：ke=50，Te=0.08 s，kL=1，TL=1.06 s，kF=0.04 s，TF=0.04 s。

調速器：Ty=0.4 s，頻率調節：bp=0，功率調節：bp=0.04。

網絡：Xe=0.2 pu，Re=0。

負荷：PH0=1，QH0=0.01，VH0=1。

水電機組采用上述參數，水電站系統初始處于額定運行狀態，水力干擾的過程：1號機正常運行，2號機組甩負荷，導葉10 s直線關閉。

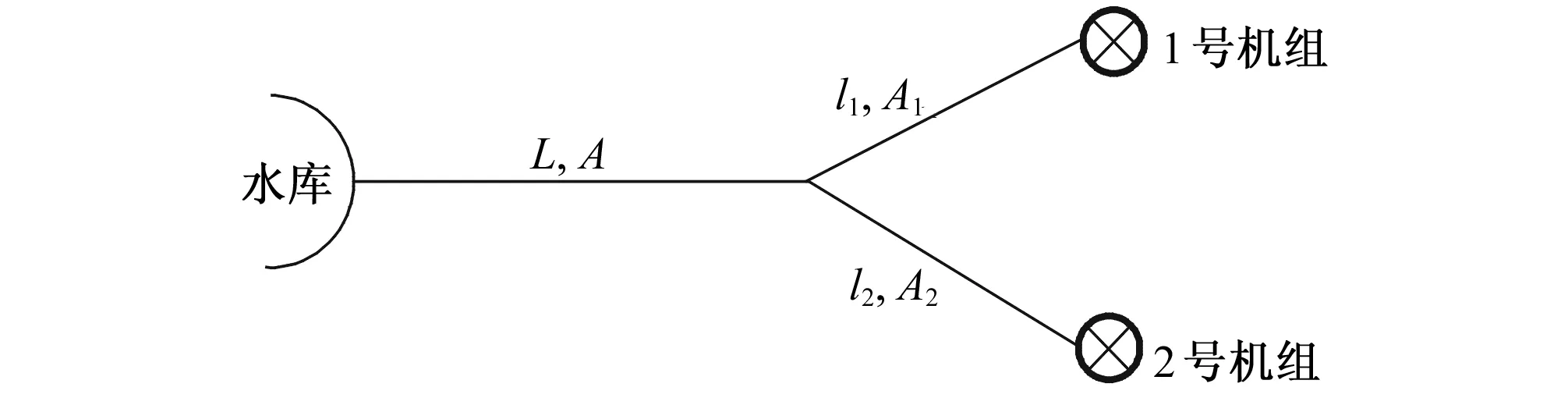
圖6 一洞兩機電站示意圖Fig.6 Diagram of single-pipe two-units hydropower plant

2.1 調速器參數對水力干擾過程的影響

根據《水輪機電液調節系統及裝置技術規程》[12]，調速器主要調節參數及其調整范圍為：暫態轉差系數bt(1%～200%)，緩沖時間常數Td(1～20 s)和加速時間常數Tn(0～2 s)，以下仿真計算中各參數均位于調整范圍內。

2.1.1機組并無窮大電網

機組并無窮大電網，采用頻率調節，因轉速恒定，則調速器不動作；采用功率調節，調速器動作以跟蹤給定功率，減小差值。發生水力干擾時，機組采用頻率調節和功率調節的結果對比如圖7所示。

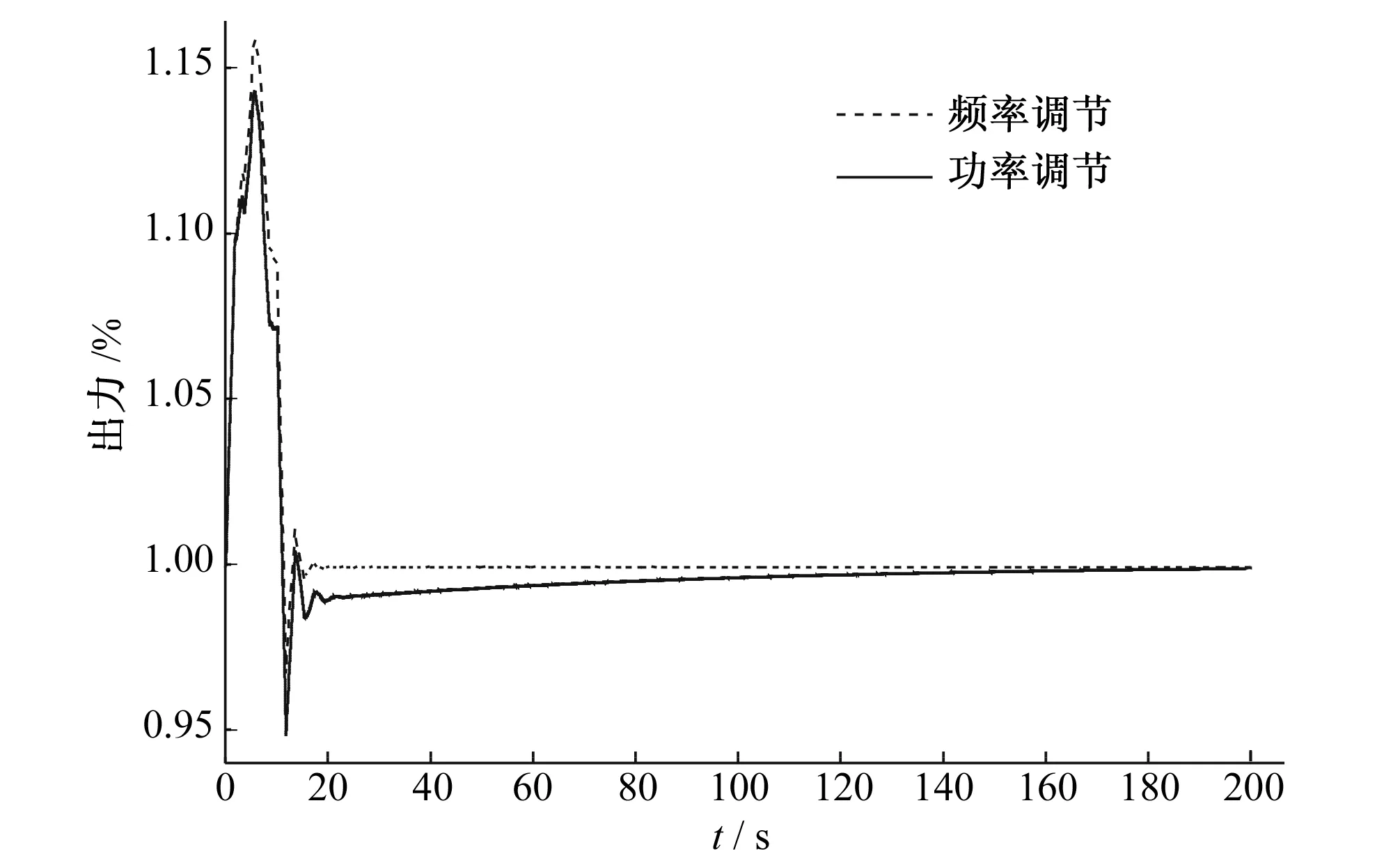
圖7 頻率調節與功率調節機組出力結果對比(bt=0.5,Td=8)Fig.7 Comparison results of Output between frequency regulation mode and power regulation mode(bt=0.5,Td=8)

由結果對比圖可知，頻率調節相比功率調節，機組出力波動幅值較大。其原因在于，水力干擾過渡過程中機組實際功率發生改變，功率調節模式下調速器動作以減小與給定功率的差值，從而減小了出力波動幅度；而頻率調節模式下，調速器對水力干擾過渡過程不做調節，機組出力波動幅度較大。因此，機組并無窮大電網，發生水力干擾應采用功率調節。

針對上述實例，對功率調節模式下調速器參數做仿真比較，結果如圖8所示。

由圖8可知，暫態轉差系數bt越小，機組出力波動幅值越小，但減小幅度有限；緩沖時間常數Td的不同取值所得出力結果基本重合，對機組出力幾乎沒有影響。因此，機組并無窮大電網，調速器參數取值的不同對水力干擾過渡過程影響較小。

2.1.2機組并孤立電網

機組并孤立電網，通常采用頻率調節模式。水力干擾過渡過程中調速器參數按小波動整定原則確定，可以保證系統穩定[5]。因此采用傳統的斯坦因推薦公式整定調速器參數作為典型參數[9]:

bt=1.5Tw/Ta=0.245 5

Td=3Tw=4.467

Tn=0.5Tw=0.744 5

對上述實例做仿真比較，結果如圖9所示。

圖8 無窮大電網條件下調速器參數對水力干擾過程的影響Fig.8 Effect of governor parameters on the process of hydraulic disturbance on the condition of infinite power grid

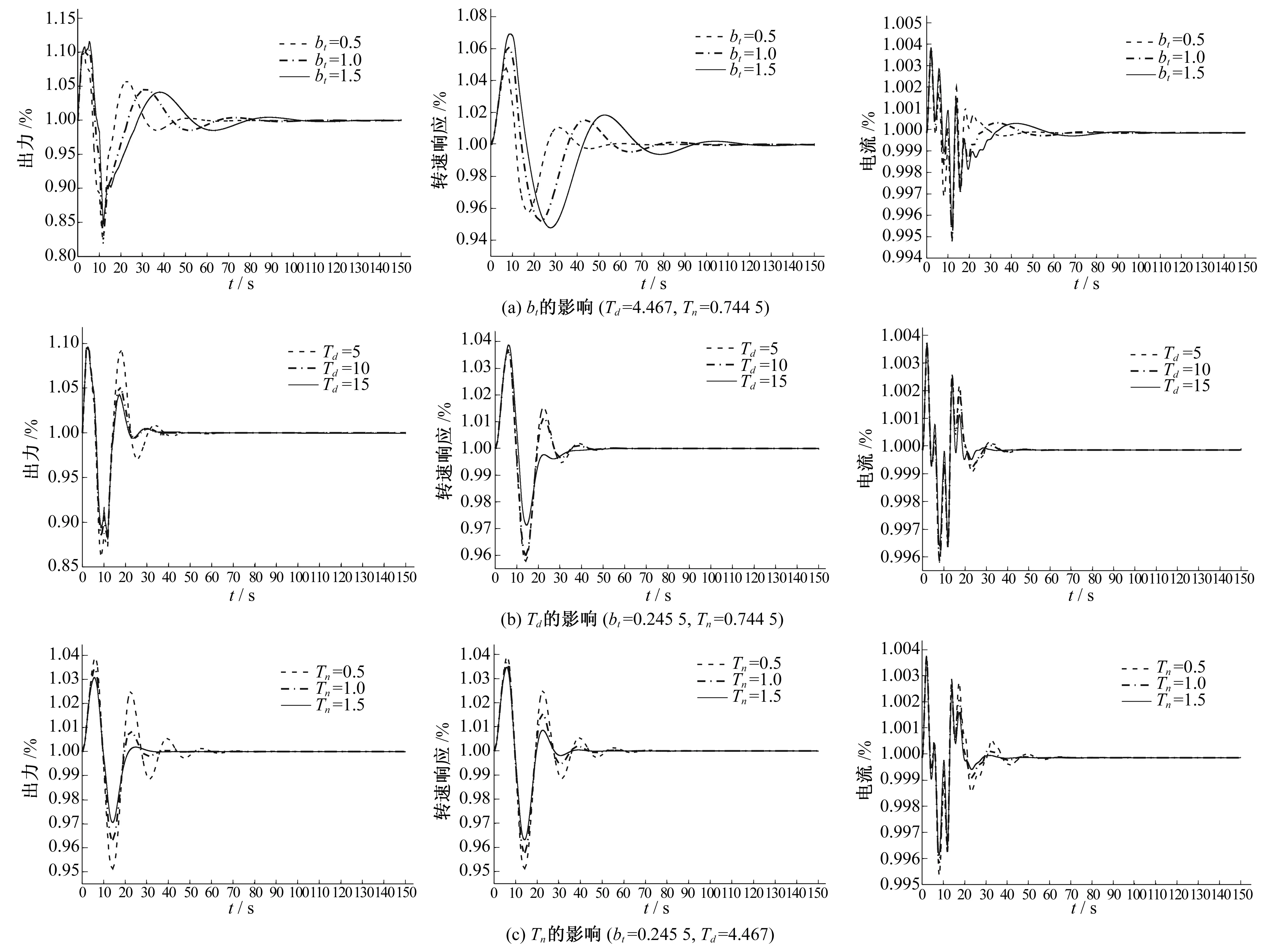
圖9 孤立電網條件下調速器參數對水力干擾過程的影響Fig.9 Effect of governor parameters on the process of hydraulic disturbance on the condition of isolate power grid

相比簡化模型僅能反映流量、壓力等水力系統物理量的動態過程，完整的水機電聯合仿真模型計算還能得出電氣側的各物理量的變化過程，如機組電流的動態過程。對比圖9中機組出力、轉速與電流動態響應可見，機組電流變化過程與機組出力、轉速變化過程基本一致，但響應速度更快，波動更明顯。

由圖9(a)可知，暫態轉差系數bt越大，機組出力、轉速及電流的超調量越大，衰減也越慢；對比圖9(b)、圖9(c)可知，相比Td和Tn，改變bt的大小對水力干擾過渡過程的影響更為顯著。

由圖9(b)可知，緩沖時間常數Td越大，機組出力、轉速及電流的超調量越大，但衰減較快；改變Td的大小對超調幾乎沒有影響，對后續衰減影響較大。

由圖9(c)可知，加速時間常數Tn越大，機組出力、轉速及電流的超調量越小，衰減越快；可見Tn取值的增大有利于水力干擾過渡過程中各物理量的調節。

綜上所述，機組并孤立電網，調速器參數取值的不同對水力干擾過渡過程影響較大，其中以bt影響最為顯著。

2.2 調速器參數的優化

機組并無窮大電網，調速器參數對水力干擾過渡過程影響較小。而機組并孤立電網，調速器參數對水力干擾過渡過程影響較大，因此本文主要研究機組并孤立電網調速器參數的優化。

Coello等提出了基于動態網格歸檔技術的多目標粒子群[13](multi-objective particle swarm optimization，MOPSO)算法，并做了實例驗證，結果表明了算法的有效性。本文根據其算法編制程序。

MOPSO算法的參數設置如下：

(1)基本參數：慣性因子ω=0.729，加速因子c1=c2=1.495，外部檔案規模為100，種群粒子數為30，最大迭代次數為50。

(2)尋優參數：水輪機調速器需要優化的參數有3個：暫態轉差系數bt，緩沖時間常數Td，加速度時間常數Tn。

(3)性能指標函數(目標向量)：性能指標函數用以評價群體中每個粒子的性能，就本文而言，優化PID參數的目標就是使得水力干擾過程中反映機組出力動態品質的超調量mp最小和調節時間ts最短；為保證系統最終穩定與機組出力最終收斂，加入第3個性能指標穩態誤差e。上述3個性能指標函數構成粒子的目標向量。

針對上述實例的水力干擾過程，運用MOPSO算法對調速器參數進行優化，從MOPSO算法的最優解集中選取超調量較小、調節時間較短的折衷解，與采用典型參數對比仿真結果如圖10所示，結果對比如表1所示。分析優化結果可得：

由圖10可知，MOPSO折衷解所得出力結果相對典型參數不僅超調量較小，振蕩幅度較小，且衰減較快。具體而言，由表1可得，MOPSO折衷解所得出力結果相比典型參數超調量減少了0.6%，調節時間減少了18.47 s。因此運用MOPSO算法獲得的尋優參數得到的出力結果超調量更小、調節時間更短、動態品質優異。

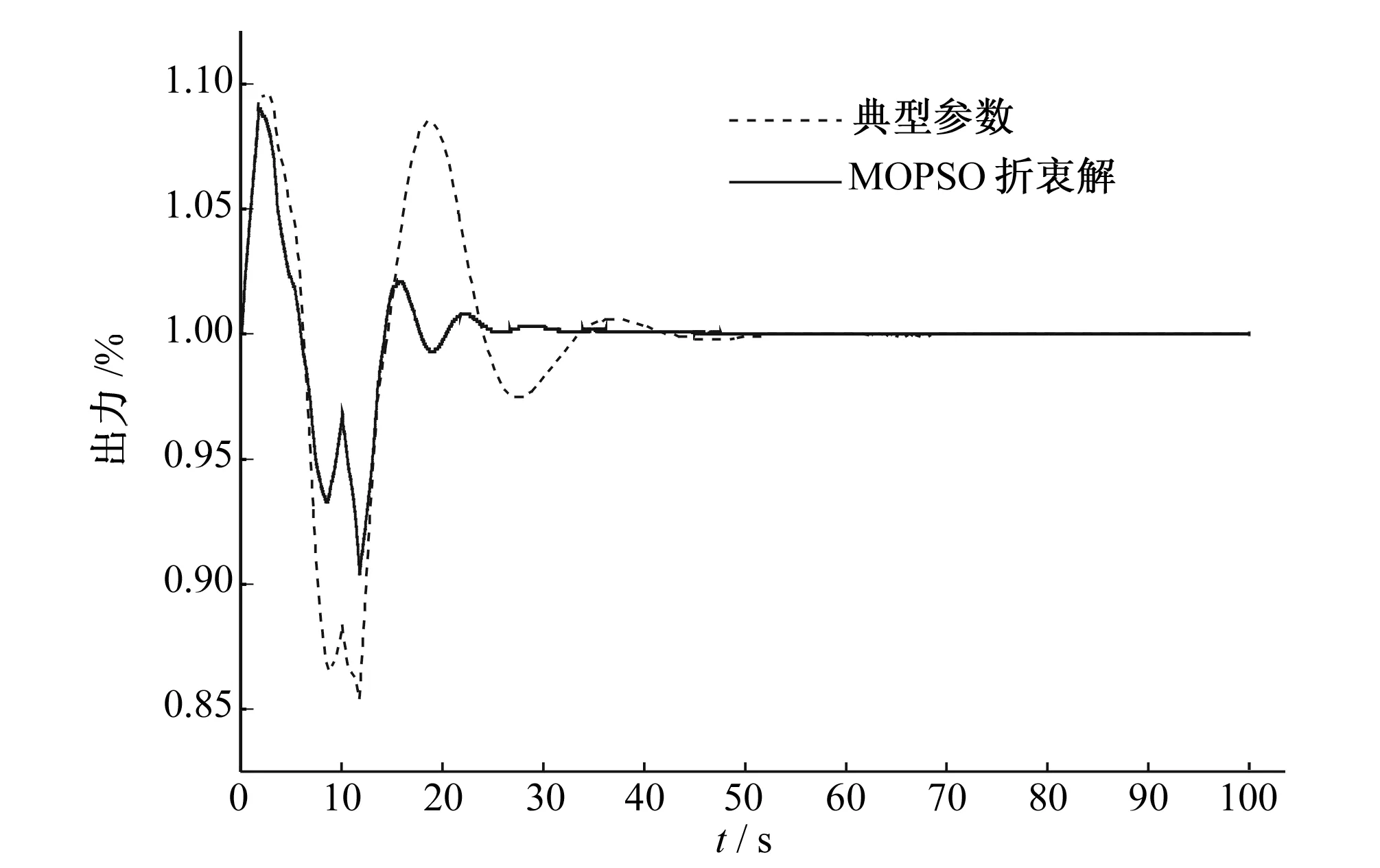
圖10 兩組調速器參數出力結果對比Fig.10 Output response of two sets of governor of optimal solution set parameters

3 結 語

本文在建立完整水機電聯合模型的基礎上，以一洞兩機電站為例，對復雜引水管道系統中的水力干擾過程進行仿真，研究了調速器參數對水力干擾過渡過程的影響，并運用MOPSO算法對水力干擾過渡過程中的調速器參數進行了優化。研究結果表明：

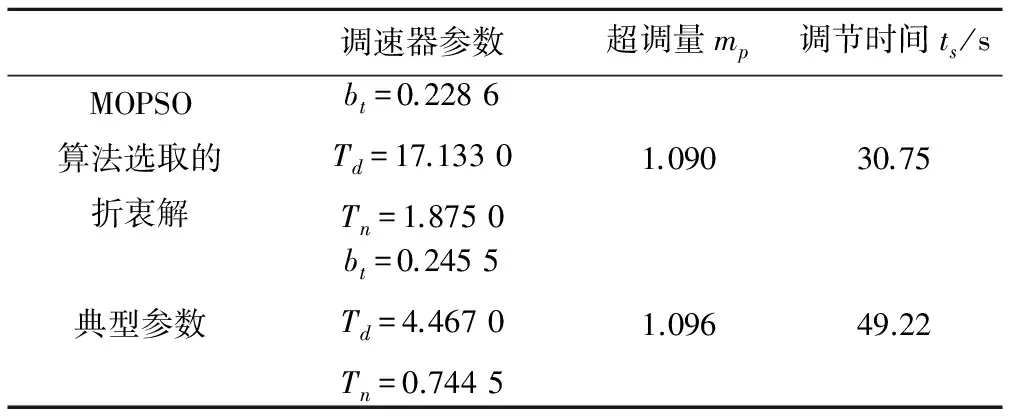
表1 MOPSO算法折衷解與典型參數結果對比Tab.1 Results of MOPSO algorithm's Compromise solution and typical parameter

(1)機組并無窮大電網，采用功率調節相比頻率調節出力波動幅值較小，但調速器參數對水力干擾過渡過程的影響較小。

(2)機組并孤立電網，調速器參數對電站水力干擾過渡過程的影響較大，其中以暫態轉差系數bt的影響最為顯著。相比以往的簡化模型，本文的水機電聯合仿真模型能更精細模擬一洞多機布置形式電站的水力干擾過渡過程。

(3)以機組出力超調量mp最小、調節時間ts最短和穩態誤差e最小為目標，運用MOPSO算法優化了孤網運行條件下一洞多機布置形式電站的調速器參數，優化后的調速器參數能使電站機組的出力獲得優良的動態品質，改善了一洞多機布置形式電站水力干擾過渡過程，提高了電站的供電質量。

□

[1] 孔慶蓉，張永良，江春波．錦屏二級水電站長引水隧洞水力特性研究[J]．水力發電，2009，35(3)：32-37．

[2] 吳世勇，周濟芳，申滿斌．錦屏二級水電站復雜超長引水發電系統水力過渡過程復核計算研究[J]．水力發電學報，2015，34(1)：107-116．

[3] 王洪亮，俞曉東，陳 勝，等．吉林臺二級水電站水力干擾過渡過程研究[J]．水電能源科學，2009，27(5)：169-171．

[4] 孫美鳳，陸桂明．高水頭引水式水電站機組之間水力干擾的研究[J]．中國農村水利水電，2002，(9)：55-58．

[5] 陳乃祥，張揚軍，屠明奇，等．抽水蓄能電站中水力干擾下的過渡過程及其穩定問題的研究[J]．水利學報，1996，(10)：68-74．

[6] 孟安波，葉魯卿，殷 豪，等．遺傳算法在水電機組調速器PID參數優化中的應用[J]．控制理論與應用，2004，21(3)：398-404．

[7] 唐正茂，馬士虎，解 德．基于外部存檔的并行遺傳算法在水輪機調速器參數優化中的應用[J]．中國電機工程學報，2012，32(28)：90-96．

[8] Wylie E B, Streeter V L. Fluid Transients in Systems[M]. Englewood Cliffs, NJ; Prentice Hall, 1993.

[9] 沈祖詒．水輪機調節[M]．北京：中國水利水電出版社，1981．

[10] 高慧敏，劉憲林．基于詳細水機電模型的水電系統動態過程仿真[J]．系統仿真學報，2003，15(4)：465-471．

[11] 鄒 金，賴 旭，宗 欣．發電機電磁過程對帶孤立負荷運行的水電站過渡過程的影響[J]．武漢大學學報(工學版)，2013，46(1)：109-112．

[12] DL/T 563-2004，水輪機電液調節系統及裝置技術規程[S]．

[13] Coello C A C，Pulido G T，Lechuga M S．Handling multiple objectives with particle swarm optimization[J]．IEEE Transactions on Evolutionary Computation，2004，8(3)：256-279．