“講道理”的課堂：生動與深刻的完美演繹
———以羅鳴亮老師的課堂教學為例

鄭梅春

一、出其不意，感受課堂靈動之美

數學課堂教學是師生之間交往互動與共同發展的過程，在這個過程中教師需要創設意料之外的驚奇，讓學生在常規處質疑，在本質中思考，激發學生主動學習的興趣，讓數學學習變得更為生動有趣，讓課堂教學充滿“出其不意”的驚喜。

例如，羅老師在執教《小數的意義》一課時，從數數入手，讓學生明白正方形卡片涂色部分不滿“1”時，用小數表示得先把卡片平均分成十份，看取幾份就是零點幾。緊接著，羅老師又借助信封，和學生玩起了“信封猜小數”的游戲。

師：我們再來猜一猜，如果老師信封里的正方形，涂色的有4塊，你們猜是哪個小數？

生：0.4。

師：一定？

生：肯定！

羅老師慢慢從信封抽出了卡片。（如圖1所示）

圖1　

圖2

生：老師，你錯了。

師：老師哪錯了？

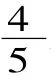
師：那還能用小數表示嗎？生1：不能。

生2：可以的，只要把這5份中的每一份再平均分成2份，變成10份，那么涂色部分就成了8份，是0.8。（如圖2所示）

師：還想繼續猜小數嗎？要什么提示？

生：要提示平均分成10份，并且知道取了幾份。

師：好！就按照你們想的來，確定平均分成10份，但涂色要比8份多。

生：0.9。生：1.0。

師：還有嗎？生：沒有了。

老師故意慢慢地把信封里的卡片抽出來。學生看到露出圖3頂端部分，都大聲高呼到“0.9”。

師：為什么是0.9？

生：因為把卡片平均分成了10份，涂了其中的9份，所以是0.9。

師：一定嗎？

生：一定！

老師把卡片完整地抽出來，學生一片嘩然。隨后，便是一陣熱烈的回應。

圖3　

圖4

生：老師，你又騙人，不是0.9！

師：不是0.9，那該用哪個小數表示呢？

生1：要把那個0.1再平均分成10份。

生2：就要把這個正方形平均分成100份。

師：為什么還要再平均分？

生3：因為不夠0.1，所以要再平均分成十份，才知道是多少。

生4：老師，我猜有可能是0.87……

在學生們爭先恐后的猜測中，羅老師分別再把卡片用課件做了如圖4所示的平均分。學生都得到了0.88這個答案，并說出了自己的想法。

在讓學生用“信封猜小數”的環節中，教師創設了平均分成5份的這一意外，讓學生經歷了從不能用小數表示到想出辦法用小數表示這一思維變化過程，深刻認識了小數是十進制分數的這一本質。接著在認識兩位小數時又出其不意地設置了懸疑，讓學生誤猜0.9，從而引出兩位小數產生的必要性。整個教學過程，學生從肯定猜測到自我否定到最后的尋求辦法解決問題，都圍繞著小數的本質進行講道理，課堂充滿思維和智慧的撞擊，學生的學習興致盎然。

二、追本溯源，領略思維深刻之美

鄭毓信教授認為：“優秀教師的特色不應局限于教學方法或模式，也應體現其對教學內容的深刻理解，反映他對學習和教學活動本質的深入思考。”對數學教師來說，在教學中，不但要向學生展示既定的數學知識，還必須能夠解釋其中的道理：為什么要認識它？它是怎么產生的？對概念、公式、定理等不能滿足于形式上的理解，而要明白其來龍去脈、知識串聯，既要重視其內涵，也要把握其外延；對數量之間或形體之間的邏輯關系要建立整體的認識，聯通各知識之間的關系，正確把握數學知識之間的因果關系。

例如，羅老師在執教《近似數》一課創設了猜“摩托車價格”的活動：

師：老師買了一輛摩托車的價格大約是8000元，猜猜，摩托車的價格實際是多少？猜對了就可以獲得獨家贊助的摩托車卡片一張。

生：可能8001。

生：8002。

生：7999。

師：還有嗎？這個價格好猜嗎？有沒有好一點的辦法？

（教師出示如下“數軸”，讓學生把猜測的摩托車價格標在數軸上）

生：我寫的是 8200，在8000前面一點。

生：我寫的是 7999，比8000少，在8000的后面一點。

生：我寫的是8000左右。

師：左右？什么意思？請到前面來表達你的想法。

（這名學生上去把7000和9000之間都用粉筆涂上了，如下圖。

全班同學都笑了，此時，教師不置可否，拿出四張卡片）

師：我把摩托車價格寫在牌子上，千位可能是幾？

生：7或者 8。

師：如果千位是7，那百位可能是幾？

生：百位可能是0～9。

生：百位可能是5～9。

此時，前面那名涂色的學生站起來了，說了如下一段話：

生：百位應該是等于500或大于500的近似數。老師，我要上黑板擦掉一些。

說完就噌噌噌地跑上去，把原來畫的圖擦掉一部分（如下圖）。然后開始講道理：

生：要大于7500的才能約等于 8000。因為 7499靠近7000,7500后面的數才靠近8000，所以7000～7500這里的數不能要。（學生掌聲）

生：老師，我還要把8500后面的擦掉（又跑上去擦掉）。因為8500后面的數更靠近9000，那就變成約等于9000了。

師：對了，數學是講道理的，這就是為什么要“四舍五入”的道理。

學生這一自悟說理的過程，我們看到了學生原先對近似數區間的感知是不清晰的，他們知道用“四舍五入”的方法來求近似數，而對為什么要“四舍五入”卻是懵懂的。羅老師根據學生的認知特點，借助數軸的直觀，學生通過辨析、討論，加深了對近似數的認知。學生在講理過程中，逐步明晰近似數是與實際接近的數，規定“四舍五入”是因為其與實際的準確數更為接近，讓學生對于近似數能表示一個區間有了更豐富、更清晰的認識。我們可以看到，學生的思維在追溯“為什么四舍五入”的過程中逐步走向深刻。

三、推理探究，感悟數學理性之美

著名教育家蘇霍姆林斯基說：“在我們每個人的內心深處，都有一個根深蒂固的愿望，那就是希望自己是一個發現者、探究者，而在兒童的內心深處，這種愿望尤其強烈。”在教學中，要充分調動學生內心深處的探究欲望，在分析驗證中去感受數學推理所帶來的成功喜悅。

羅老師《探究 2、3、5倍數特征的道理》一課，讓我們深刻領略到，學生在推理探究過程中從內心所煥發出來的對數學學科的喜愛。

問題：為什么判斷一個數是不是5的倍數只要看個位數，其他數位都不用看？

師：先獨立思考，再同桌交流。

生：雙數個5相加個位是0，單數個5相加個位是5，自然數能分成兩類，一類是單數，一類是雙數，所以答案末尾必須是0或 5。

生：我和我的同桌有一種想法，就是一個奇數乘以5，它的個位一定是5；一個偶數乘以5，它的個位一定是0。

生：我有補充，如果去掉個位的話，末尾就是0，末尾為0的一定是5的倍數，所以只要看個位是不是5的倍數就行了。

師：誰聽懂了他的想法？

生：他的意思是，不管多大的一個數，去掉個位余下的數一定是整十數，再加個位上的5或者是0，這樣的一個數肯定是5的倍數。

師：（在計數器的十位上撥1）是不是5的倍數？（是）為什么？

生：因為它表示1個十，一個十是5的倍數。

師：（將計數器藏在桌底下）我在十位上撥，還是不是5的倍數？（是）你們沒看到，怎么還能肯定？

生：因為每個十都是由2個5組成的，無論十位上撥幾個十都是5的倍數。

師：我在百位上撥，還是5的倍數嗎？（是）為什么？

生：100里面有10個十，十是可以被5整除的，10個十除以5等于20，百位表示的是有幾個百，不管幾個百都是5的倍數。

師：猜猜接下來我會在哪一位上撥？

生：千位。

師：對不起，你們都猜錯了。我為什么不在千位上撥了？

生：因為千位跟百位、十位都一樣。1000是由10個一百組成，而一百是5的倍數，所以千位不管是幾都是5的倍數。

師：（將計數器藏在桌底下）我在個位上撥，還是5的倍數嗎？

生：不確定。

師：現在為什么不確定？

生：假如你撥了1個，就不是5的倍數；在個位撥5才是5的倍數。

生：現在我明白了為什么判斷是不是5的倍數只看個位，其他數位不用看的道理了。

師：5的道理是這樣，想想5的道理和哪個數是一樣的？

生：和2是一樣的，個位上是 0，2，4，6，8 的數，都是 2 的倍數。

師：為什么只看個位呢？

生：10是5個 2，100是 50個2，1000是500個2。個位上只有 2，4，6，8 是 2 的倍數，3 和5都不是2的倍數。

師：那3的倍數，為什么要看各位上數的和？

生：因為3的倍數的個位是不確定的，可能是0，可能是1，可能是2……所以不能只看個位，得總體來看。

師：為什么個位不確定？為什么要總體來看呢？

生：因為10不能被3整除，還有余數，所以每個數位都要看。

師：那為什么判斷3的倍數又要把各個數位上的數加起來呢？你們能試著研究嗎？

……

推理可以分成合情推理與演繹推理，其中合情推理包括歸納推理與類比推理，本節課，羅老師讓學生自主探究，把推理方法應用得淋漓盡致。5的倍數為什么只看個位，學生從舉例入手，從十位不用看類推到百位、千位等都不用看的道理，從而歸納出5的倍數只看個位的道理。而從5的道理又類比遷移推理到2為什么也只看個位，3卻要看各個數位。整個過程，學生不斷地調動思維進行講理，在比較、判斷中，逐步推理出判斷數的倍數特征背后潛在的道理。在判斷3的倍數為什么要計算各個數位之和，更是把演繹推理和合情推理有效結合，讓學生真正喜愛上了探究，以至于在課的最后，學生發出如此的感慨：“我覺得平時我們上數學課老師直接教我們方法，這節課我們是尋找為什么要這樣做。刨根問底，總結方法。”“這一節課不知道有沒有改變其他人，但至少改變了我，顛覆了我對數學的理解。學習數學不是簡單地記住公式就可以了。”學生在這節課上，充分感受到了數學理性的魅力。

鄭毓信教授提出：數學教育主要應當促使學生更為積極地去進行思考，并能通過數學學習學會思維，特別是能逐步學會想得更深、更合理、更清晰、更全面。從羅老師的課堂我們看到了：讓學生在尋求數學本質的過程中明晰數學道理，真正讓數學課走向“深刻”和“生動”，這樣的“講道理”課堂，正是我們學生所喜愛的、教師所追求的精彩課堂！