風洞MDOE的形式實驗設計方法研究

張 江，秦永明，馬漢東

（中國航天空氣動力技術研究院，北京 100074）

風洞MDOE的形式實驗設計方法研究

張 江＊，秦永明，馬漢東

（中國航天空氣動力技術研究院，北京 100074）

MDOE風洞實驗方法能夠用相對于傳統實驗方法更少的吹風次數，獲得更高精準度的數據。為了解決現有基于參數模型的MDOE方法獲取較強非線性氣動規律能力的不足，需要發展基于非參數模型的MDOE方法。本文對基于非參數模型的MDOE的形式實驗設計方法進行研究。通過“虛擬”風洞實驗的方法，對兩種常用的“空間填充設計”——拉丁超立方設計和均勻設計應用于風洞實驗的適用性進行對比，并在此基礎上發展了幾種對均勻設計的優化改進方法，可以進一步提高樣本點設計質量，使其滿足風洞實驗的要求。研究表明：均勻設計較拉丁超立方設計更為穩健、均勻，更適合基于非參數模型的風洞MDOE方法；在均勻設計方法基礎上，根據風洞實驗的特點發展了優化方法，包括邊界點補充、樣本點密度調整和重復點設計，能夠將已有的“先驗信息”應用于實驗設計中；所發展的形式實驗設計方法所需的測量點要少于OFAT方法的測量點（如示例中所用的測量點數僅為OFAT方法的66.7%），且能夠充分和準確地對較劇烈的非線性變化規律進行采樣。本文對風洞MDOE的形式實驗設計方法的研究結果，為后續發展基于非參數模型的風洞MDOE方法奠定了基礎。

MDOE；非參數模型；均勻設計；拉丁超立方；風洞實驗

0 引 言

現代風洞實驗測試系統的構成越來越復雜，增加了實驗中各環節的微弱變化所導致的系統誤差來源，使得風洞實驗誤差的控制難度加大，同飛行器設計不斷提高的數據質量要求之間的矛盾越來越突出。傳統的單因子實驗方法（OFAT方法）對實驗環境變化導致的誤差缺少控制和消除能力［1］，且生產效率過低［2］。現代實驗設計（MDOE）領域的研究表明通過改進實驗設計，能夠有效地減小甚至消除實驗環境中不可控因素對實驗結果的影響。風洞MDOE實驗方法就是將現代實驗設計理論應用于風洞實驗產生的新技術，它能夠用相對少量的實驗次數，獲得更高質量的數據。

MDOE方法通過建立統計模型來獲取氣動規律。統計模型有方差分析模型、參數回歸模型、非參數回歸模型和穩健回歸模型等。形式實驗設計方法是MDOE的重要組成，是對測量樣本點數量和取值進行設計的方法。不同的統計模型需要不同的形式實驗設計方法。方差模型適用于因素線性效應的研究，采用具有合適分辨力的部分因子設計［3］，可以通過較全因子設計更少的實驗次數，計算出主因素的效應和交互效應，并且有效避免主因素與交互作用及交互作用間出現混淆（Confounded）現象。參數回歸模型能夠給出氣動力系數隨姿態角、馬赫數、控制面偏轉角等自變量變化的非線性規律，在風洞MDOE中被廣泛應用［4］。基于參數回歸模型的MDOE的形式實驗設計方法有中心復合設計（Center Composite Design，CCD）、面心復合設計（Face－centered Central Composite Design，FCD）和最優回歸設計（Optimum Design）等［5－6］。這些設計方法都屬于回歸設計，在進行設計前要確定氣動模型的結構形式。

隨著現代戰斗機和導彈對機動性要求的不斷提高，飛行器氣動力規律通常是非線性和多變量耦合的，基于參數回歸模型的MDOE方法已經不能滿足要求。當氣動規律的非線性較強時，基于多項式的響應面模型難以很好地對全局氣動規律進行擬合［7－8］。由于非參數模型較多項式模型有更強的非線性建模能力，所以基于非參數模型的MDOE方法逐漸被人們所關注［9］。非參數模型的形式實驗設計一般采用拉丁超立方設計（Latin Hypercube Sampling，LHS）和均勻設計（Uniform Design），在風洞MDOE中還沒有相關的研究。本文針對風洞非參數模型MDOE的形式實驗設計方法開展研究，采用Kriging方法進行建模，對拉丁超立方設計和均勻設計應用于風洞實驗的適用性進行比較，并根據風洞實驗的特點發展相應的優化方法。

1 研究方法

為了深入分析研究不同的實驗設計方法的優缺點，本文通過建立標模實驗氣動模型，進行“虛擬”風洞實驗。“虛擬”實驗是實驗設計方法研究中常用的方法，實驗設計方法研究中需要頻繁地對各種設計進行比較和優化，真實的風洞實驗周期長、成本高，而虛擬風洞實驗可以及時地獲得結果，采用這種方法能夠高效、低成本地進行實驗設計方法的研究［10］。本文所采用的實驗氣動模型是利用在中國航天十一院FD－06風洞已有的大量標模實驗數據構建的。輸入一組新的設計樣本點，就可以獲得該樣本對應的六分量氣動數據和不確定度，完成一次“虛擬”的風洞實驗過程。然后根據虛擬風洞實驗結果，進行建模和數據分析，通過和實驗氣動模型（即標準響應面）相比較，考核其還原氣動模型的能力。

自變量的設計空間如下：

迎角：0°～40°；

滾轉角：0°～90°。

響應變量：法向力系數CN，前體軸向力系數CAF，側向力系數CZ，俯仰力矩系數mzg，偏航力矩系數myg和滾轉力矩系數mx。

檢驗設計優劣除了通過數據和繪圖直接對比外，還利用統計方法對各種設計方法建立的響應面模型的近似精度進行比較。選擇一定量均布于設計空間的檢驗點，分別代入標準響應面和樣本點建立的響應面模型得到標準值yi、預測值y＾i和預測值的不確定度Ui，采用整體均方根誤差RMSE和判定系數R2對新響應面模型的擬合程度進行評估，采用整體平均不確定度M＿U 對預測誤差進行評估，公式分別如下：

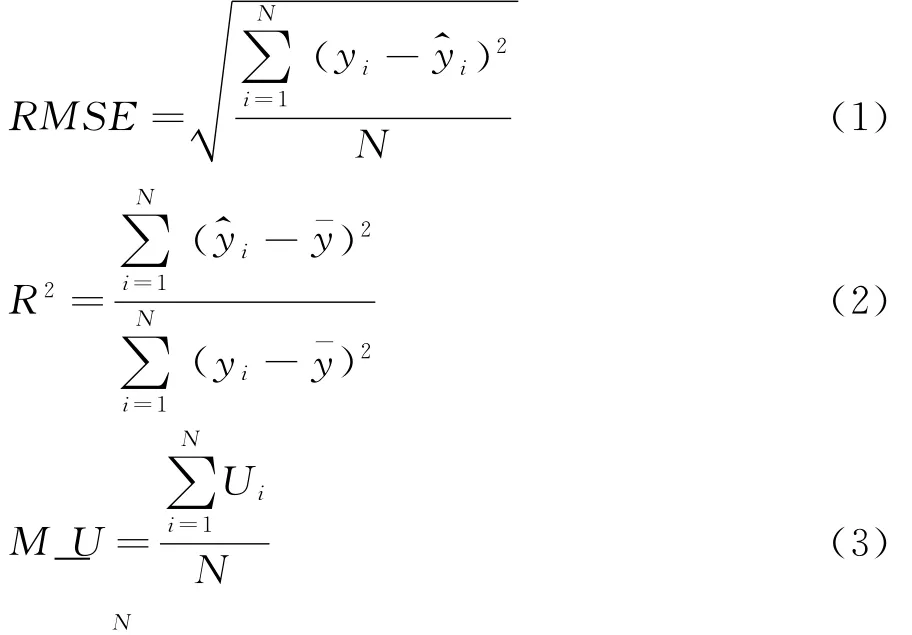
2 MDOE風洞實驗設計方法的選擇

拉丁超立方設計和均勻設計，二者也被稱為是“空間填充設計”［11］或者“空間抽樣設計”［12］。“沒有最好的設計，只有最適合的設計”［13］，本文根據風洞實驗的特點，對這兩種方法的適用性進行研究。

2.1 拉丁超立方設計

拉丁超立方法是應用廣泛的現代實驗設計技術之一，取樣覆蓋均勻，適用于影響因素較多的情況，可顯著減少實驗規模［14］，實驗次數等于水平數。拉丁超立方抽樣是按如下方法選取設計點的：

設有n個設計變量，每個變量p個水平，拉丁超立方抽樣將每個設計變量分為p個區間，因均勻分布，p個區間等間隔。這樣整個變量空間分成pn個了區域。遵循下列兩個原則取實驗點：

1）樣本點在每個了區域隨機選取；

2）在任一維，即任一變量上的投影有p個區間，每個區間有且僅有一個樣本點。

由于拉丁超立方設計是一種隨機抽樣設計方法，容易產生分布不均勻的較差設計，所以通常加以一定的準則以保證其均勻性，常用的準則有最大最小距離（Maximize minimum distance）、最小最大距離（Minimize maximum distance）、最小差異準則（Minimize discrepancy）、相對理想累積分布最小均方根差異準則（Minimize RMSvariation from CDF）和相對理想累積分布最小最大差異準則（Minimize maximum variation from CDF）。本文對以上幾種準則條件下的LHS設計進行對比。設計樣本點為40個，通過“虛擬”風洞實驗獲得樣本數據，然后用樣本數據建立樣本點響應面和標準響應面進行比較。

對于模型的6個氣動力和力矩分量，需要建立6個響應面。通常縱向氣動系數的響應面模型非線性程度要比橫向的弱，如果樣本點能夠滿足橫向氣動系數響應面模型的建立，縱向也能夠滿足。圖1～圖5給出了基于上述5種不同準則下的LHS樣本設計及其建立的滾轉力矩系數mx響應面。表1給出了檢驗點的統計分析結果。

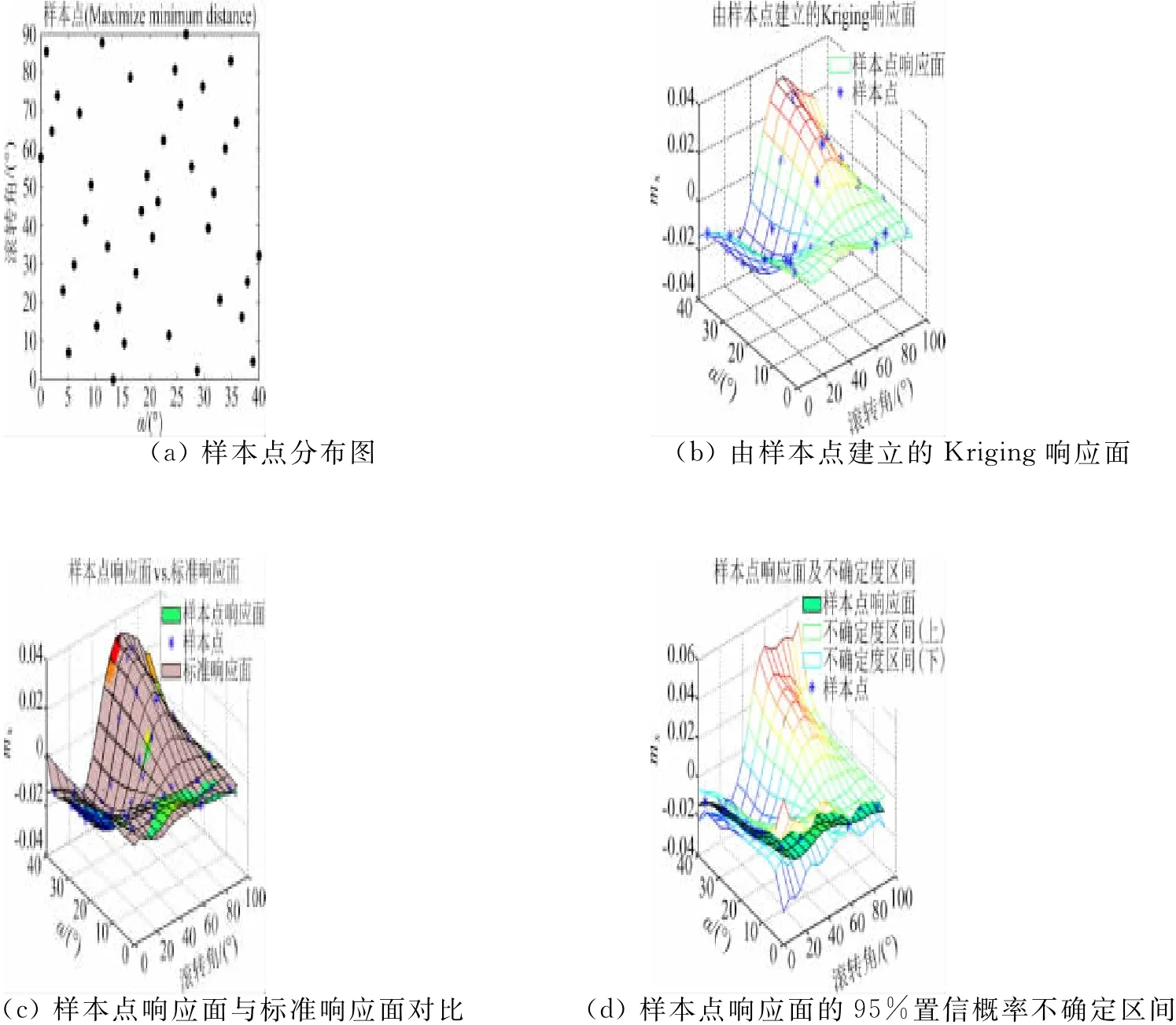
圖1 LHS樣本點及響應面（最大最小距離準則）Fig.1 Sample points of LHS design and the response surface（Maximize minimum distance）

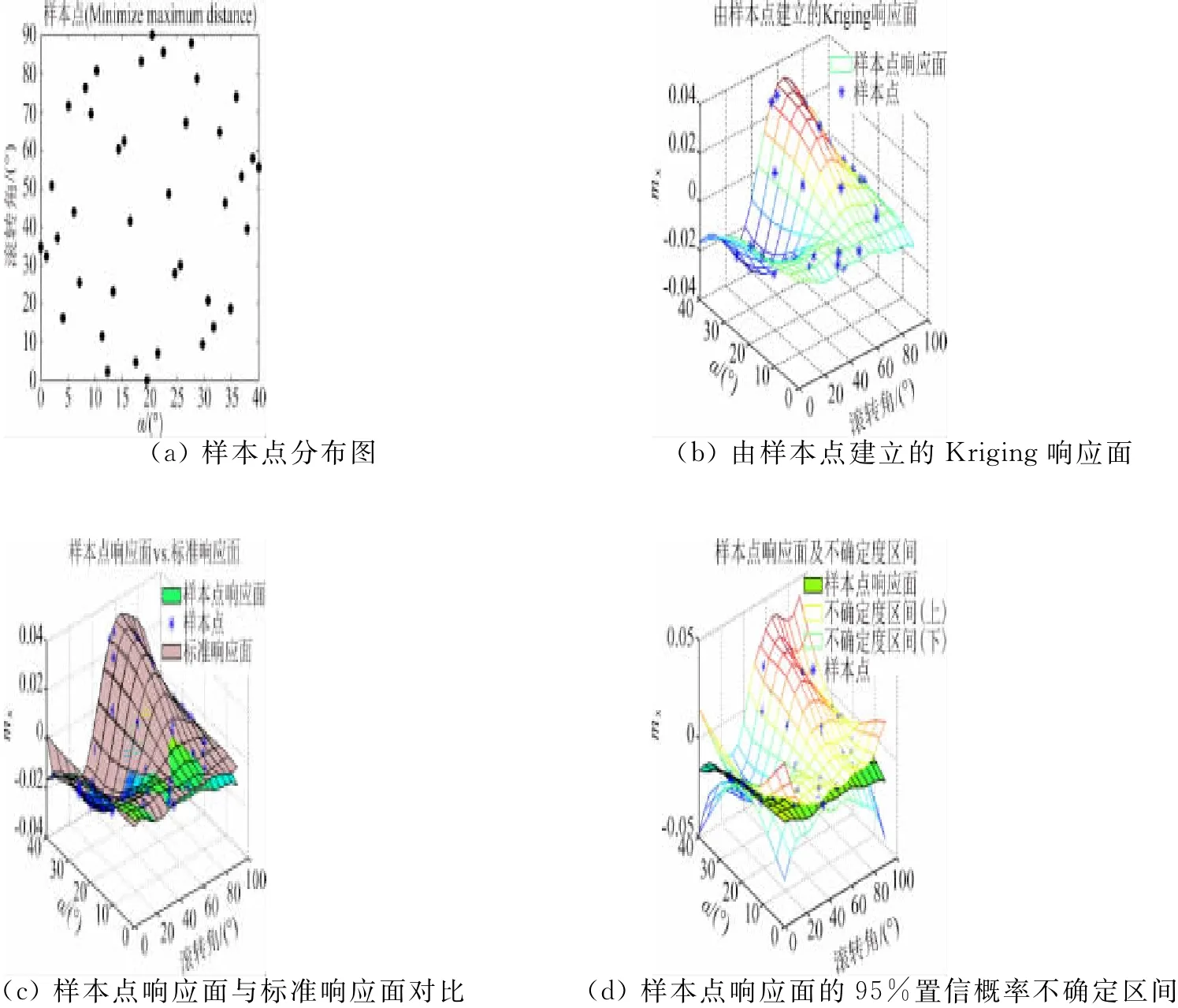
圖2 LHS樣本點及響應面（最小最大距離準則）Fig.2 Sample points of LHS design and the response surface（Minimize maximum distance）

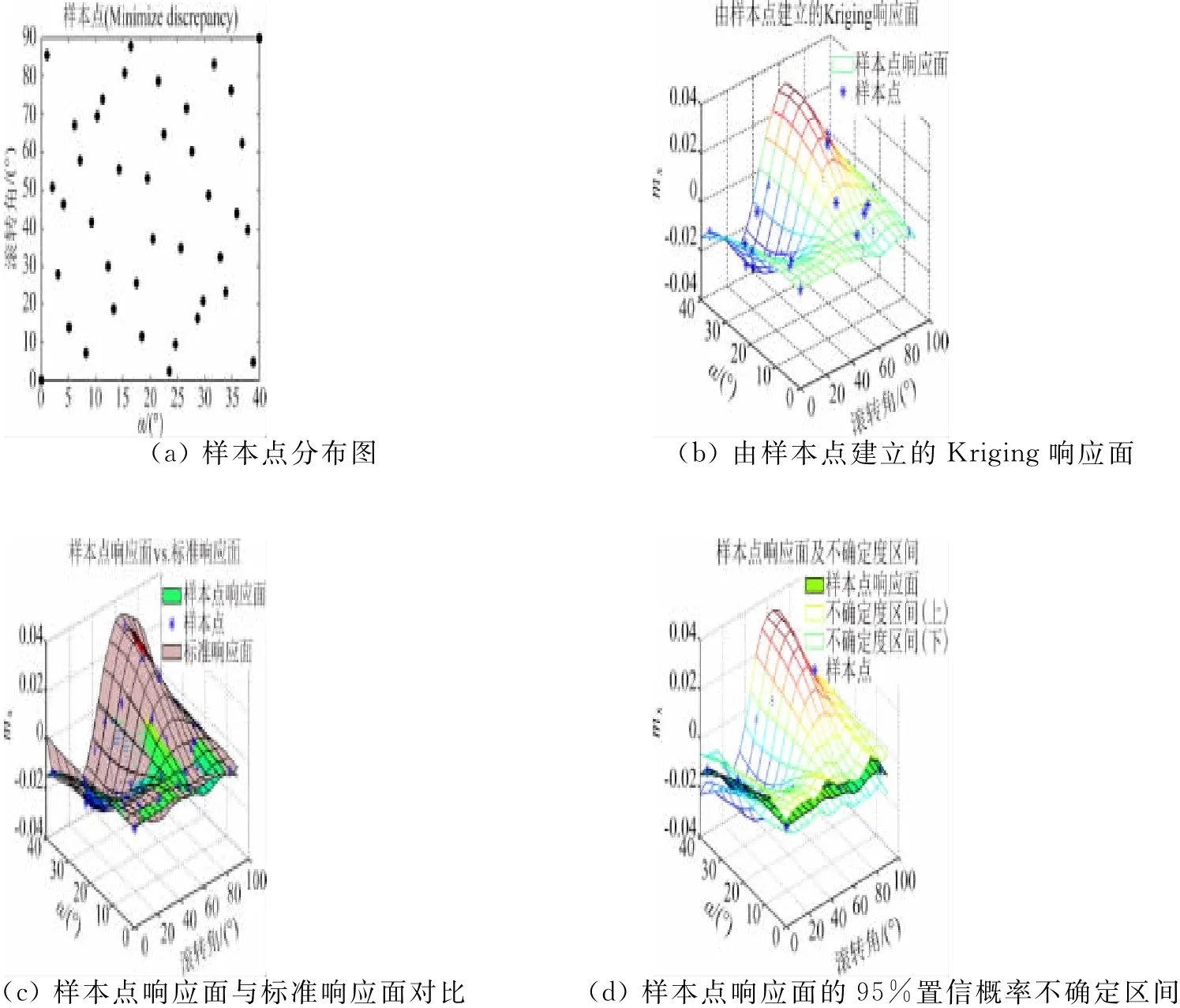
圖3 LHS樣本點及響應面（最小差異準則）Fig.3 Sample points of LHS design and the response surface（Minimize discrepancy）

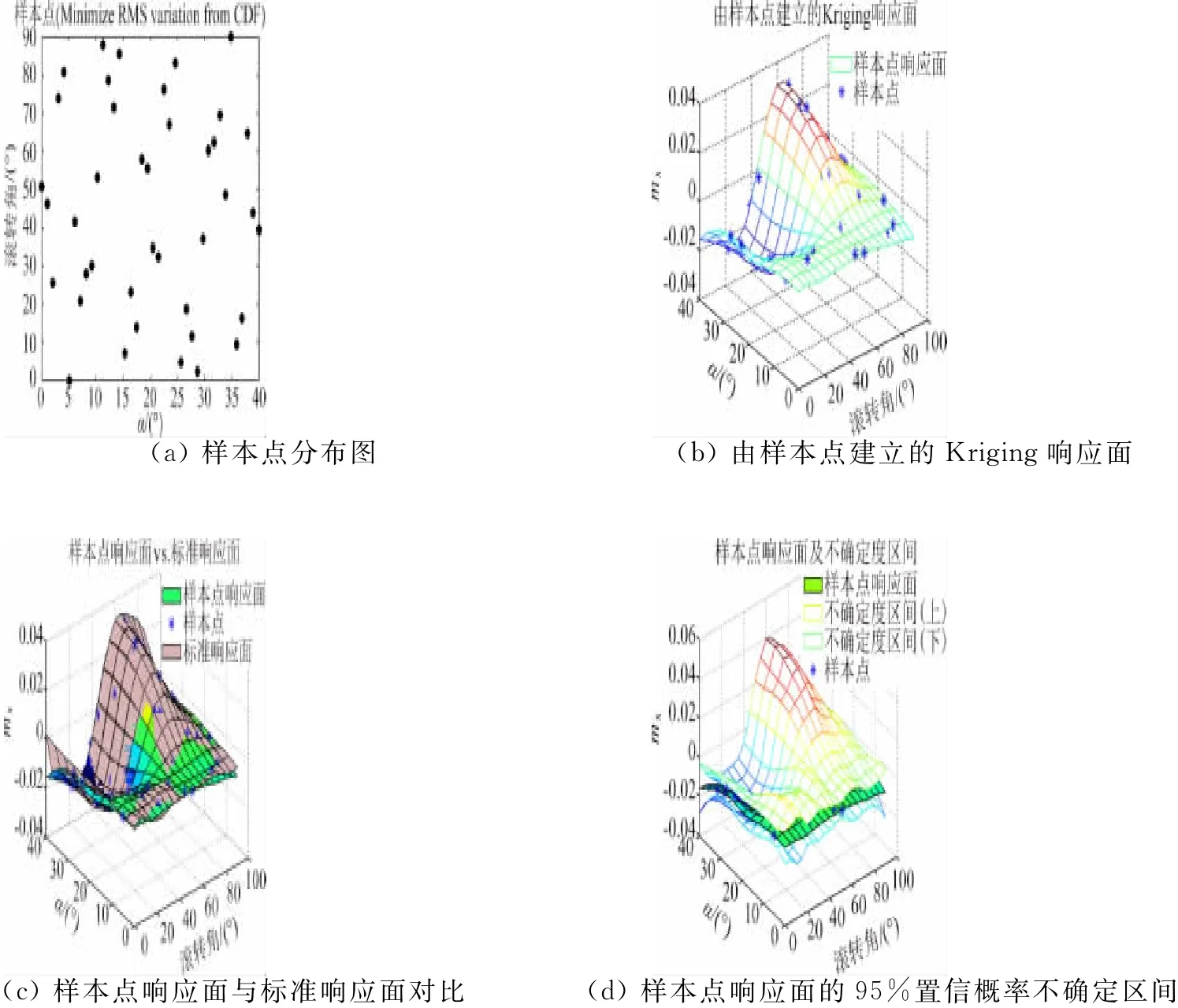
圖4 LHS樣本點及響應面（相對理想累積分布最小均方根差異準則）Fig.4 Sample points of LHS design and the response surface（Minimize RMS variation from CDF）

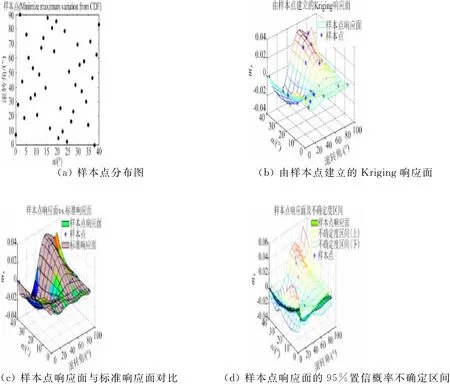
圖5 LHS樣本點及響應面（相對理想累積分布最小最大差異準則）Fig.5 Sample points of LHS design and the response surface（Minimize maximum variation from CDF）

表1 不同LHS設計方法的響應面檢驗結果Table 1 Test results of the response surfaces of different LHS designs

從檢驗參數看，不同準則下的LHS設計的整體模型精度均較高，差異不明顯。從樣本點響應面與標準響應面對比圖可以看出，如果在某局部區域缺少樣本點，就容易出現局部預測誤差較大的問題，如滾轉角0°、迎角接近40°附近，預測響應面的mx普遍偏大，而標準響應面的mx在此處為小量。只有采用了相對理想累積分布最小最大差異準則的LHS樣本點的響應面（圖5），其原因是該設計在此位置有一個樣本點。

所以，LHS設計盡管已經采用了一些促進其“均勻化”的準則，但仍然容易出現某個局部沒有樣本點的情況，這會導致較大的預測偏差和不確定度，是風洞實驗難以接受的。其次，LHS的樣本點生成有隨機性，帶來兩個問題：一是每次設計的質量會有差異，穩定性不高；二是每次設計中樣本點分布不佳的區域和程度不同，不便于進行優化。

2.2 均勻設計

均勻設計［15］由我國方開泰和王元院士提出，是一種空間填充（Space Filling）設計。均勻設計要求實驗點均勻的分布在實驗區域內，均勻設計基于偏差來衡量樣本點在設計空間分布的均勻性，使得設計空間內各區域能夠均等的“獲得”樣本點信息，每個樣本點所承載的信息也能夠在建模中被充分利用，這一優點非常適合MDOE風洞實驗設計。

均勻性準則要求設計具有最好的均勻性，對于一個設計，若沒有其他設計比它有更小的偏差，則稱該設計為均勻設計［16］。為了衡量設計的均勻性，人們提出了偏差這個概念來衡量實驗點集在實驗區域內散布均勻程度。不失一般性，假設實驗域為Cs＝［0，1］s。記P＝｛x1，…，xn｝＝（xij）n×s為Cs上的一個有n個實驗點的設計，它可表為n×s的矩陣，其中n表示實驗點數，s表示因子的個數。Hickernell［17］用泛函分析中再生核Hilbert空間的方法將古典的諸偏差表成統一形式，并且定義了許多新偏差，其中應用得最廣泛的是如下的中心化L2－偏差CD（P）：

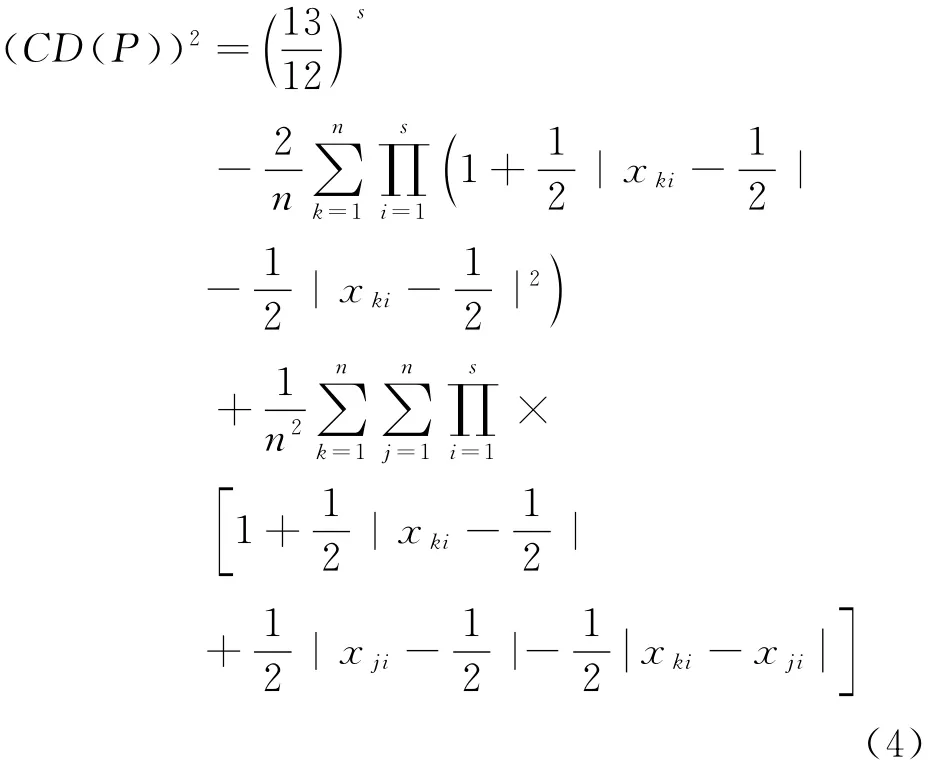
和可卷型L2－偏差WD（P）：

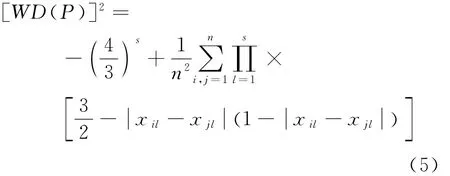
進行樣本點數量為40個的均勻設計，圖6（a）給出了一個設計結果，表2給出了樣本點的偏差計算和響應面檢驗結果。均勻設計的樣本分布整體上非常均勻，沒有較明顯的“團聚”和“缺失”區域，所建立的響應面檢驗結果也優于LHS設計結果。從圖6（c）和6（d）可以看出，除了設計空間的邊緣位置外，樣本點響應面和標準響應面吻合良好，沒有差異或不確定度特別大的局部區域。

所以，對于風洞實驗均勻設計較LHS更為穩健、均勻，更適合在MDOE風洞實驗中應用。

表2 均勻設計樣本點的偏差計算和響應面檢驗結果Table 2 Discrepancies of Uniform Design and test results of the response surface

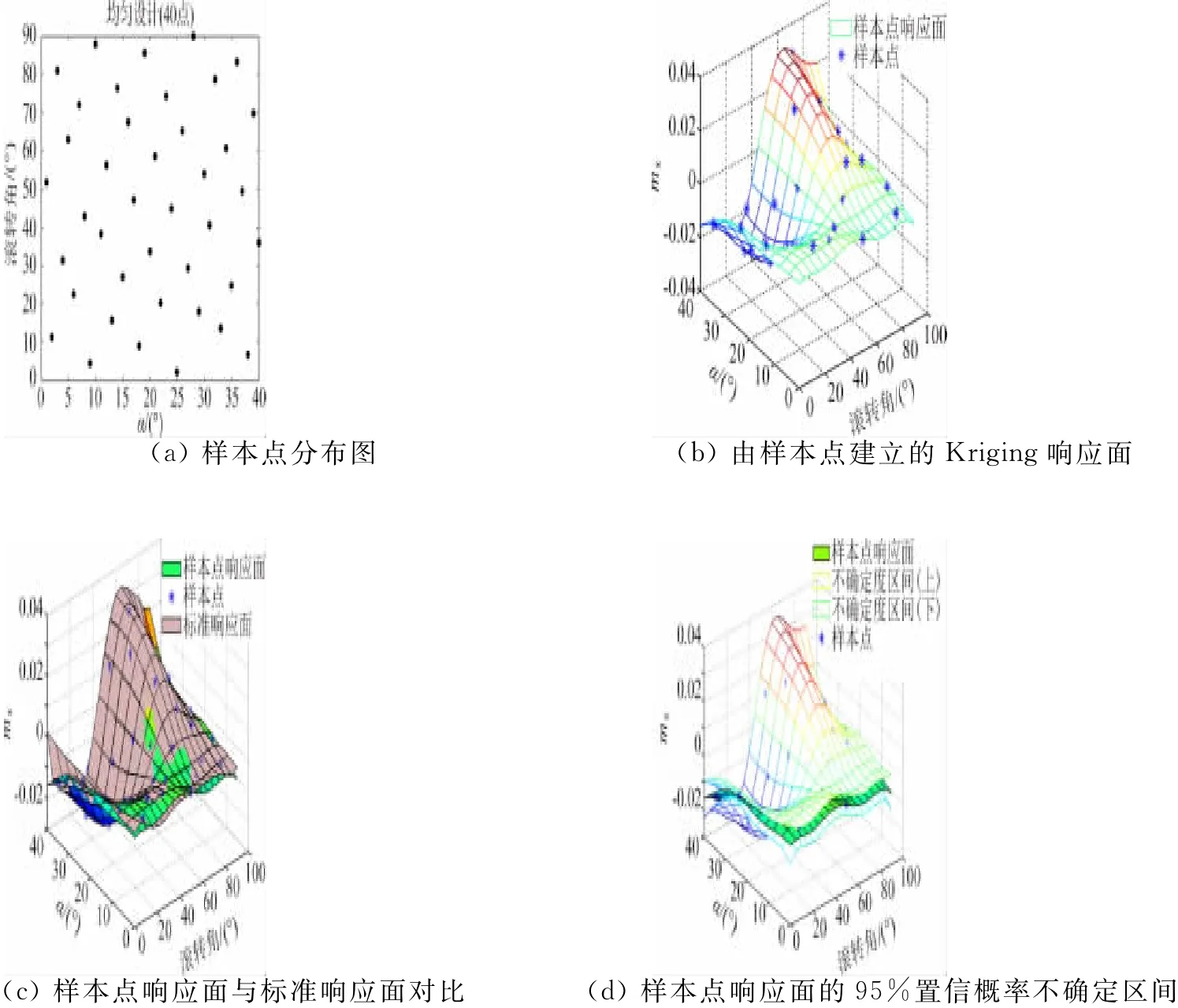
圖6 均勻設計樣本點及響應面Fig.6 Sample points of Uniform Design and the response surface

3 均勻設計應用于MDOE風洞實驗的優化與改進

均勻設計得到初始實驗設計結果還無法滿足風洞實驗的要求，還要根據風洞實驗的具體特點加以優化。本文發展了幾種對均勻設計的優化改進方法，可以進一步提高樣本點設計質量，使其滿足風洞實驗的要求。

3.1 邊界點補充

對于飛行器氣動模型，邊界位置的數據質量往往是非常重要的，而且當飛行器處于最大姿態角位置時，氣動規律出現非線性的可能性增大，要求數據盡可能內插，以防止外插帶來的風險。邊界點的增加包括角點和邊線點，補充邊界點后的設計如圖7所示。補充邊界點時先將設計空間進行了標準化，即將各自變量范圍轉換到［0，1］區域內，補充方法如下：

1）角點直接在設計空間角點增加，即［0，0］，［0，1］，［1，0］，［1，1］；

2）計算原始設計樣本間的最大最小距離Dmaxmin，即每個樣本點和其他點的最小距離中的最大值，本例中Dmaxmin為0.190 39，出現Dmaxmin的兩個點在圖7中用“☆”標記；

3）確定邊界影響區域范圍，這是給邊界提供建模信息的區域，通過判斷該區域點的分布來決定邊線點增加的位置。如本例取0.1作為劃分界限，距離四個邊界為0.1的點視為邊界影響區域樣本點，在圖7中用“＋”標出。

4）對邊界影響區域樣本點在其邊界方向的距離進行判斷，如果距離大于Dmaxmin，則在邊界以等分方式增加樣本點，直至邊界影響區域樣本點在其邊界方向的距離都小于Dmaxmin，結果如圖7所示。

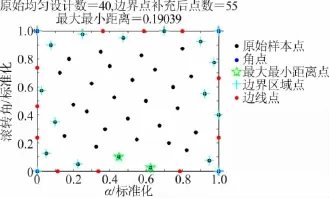
圖7 均勻設計邊界點補充示意圖Fig.7 Boundary points filling of Uniform Design

3.2 樣本點密度調整

為了提高實驗數據的精確度，風洞實驗中常常在會發生氣動規律劇烈變化的自變量區域，或者研究者特別關注的實驗狀態附近，減小實驗點間隔，增加樣本點。均勻設計的樣本點在設計空間內“均勻散布”，適合于研究中各區域的信息密度需求相同的情況。當有先驗信息時，在其基礎上改變樣本點分布密度，更符合風洞實驗的實際。圖8給出了迎角方向改變密度分布前后的對比，對于迎角0°～12°范圍的樣本點，迎角方向間隔增加到1.2倍，多出的點移入12°～40°的區間；迎角12°～40°范圍的樣本點，迎角方向間隔減小為原來的0.914 3倍。由于迎角大于12°后氣動規律隨迎角變化更為強烈，改變密度分布后迎角12°到40°的區間樣本點增加了2個，提高了大迎角區域的樣本點密度，更為合理。

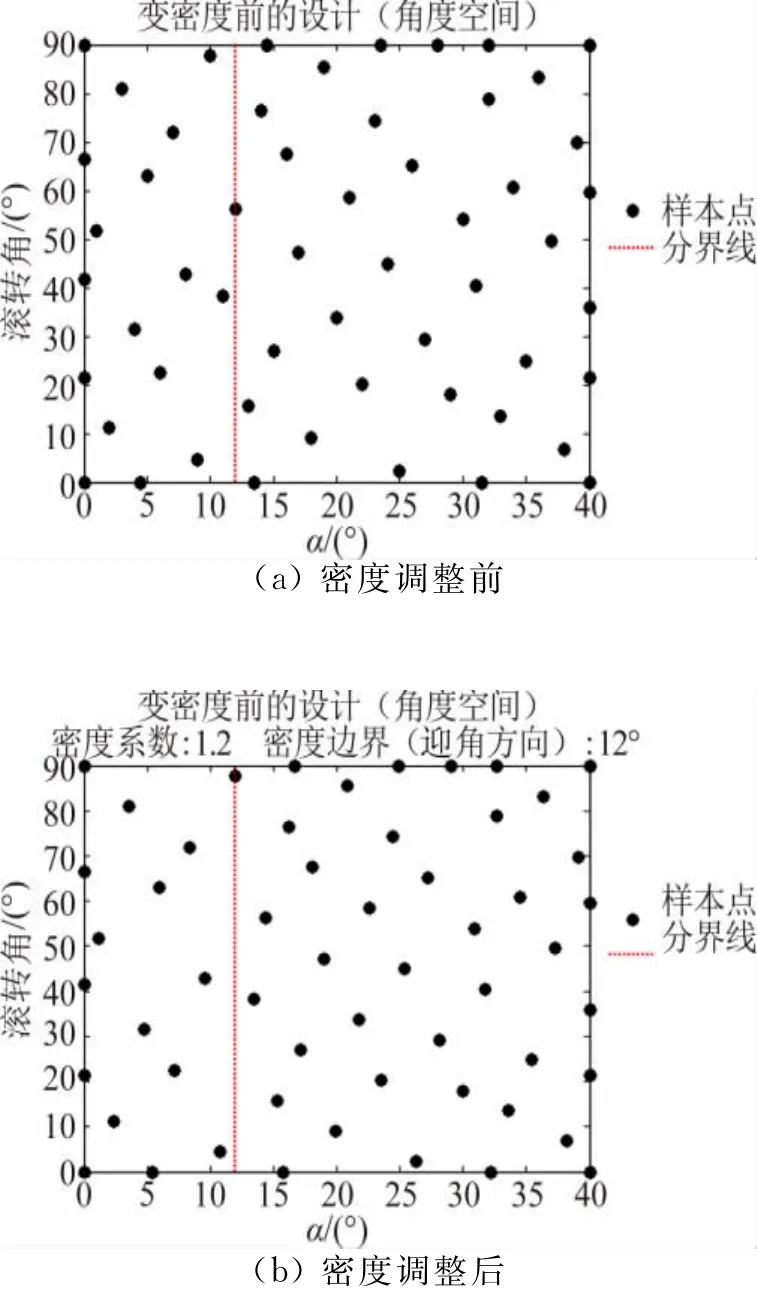
圖8 樣本點密度調整前后對比Fig.8 Comparison the distributions of pre－and－after adjusting of the density of sample points

3.3 重復點設計

重復點數量由實驗的不確定度目標和實驗環境所決定，實驗環境誤差大，要獲得高質量水平的數據，重復的次數需要多些。重復點的設計可以根據先驗來決定，如在規律變化劇烈或評價檢測風洞系統穩定性的某些關鍵位置。除此之外，角點和邊線點位置也是設置重復點的重點區域。對設計空間的內部點，重復點設置可以隨機選擇，也可以按照均勻設計方法進行選擇，圖9給出內點重復設計的結果。

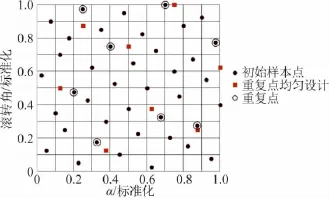
圖9 設計空間內重復點的設計Fig.9 Design of the repetitive points in the design space

4 應用示例

本節將均勻設計及其優化方法應用于基于Kriging模型MDOE實驗，設計變量為迎角和滾轉角。

4.1 實驗條件

風洞模型為導彈類標模，外形為舵身組合體，四片尾舵在0°滾轉角時呈“X”字布局。實驗馬赫數為1.79，自變量的設計空間為：迎角0°～40°；滾轉角0°～90°。

OFAT實驗的實驗測量點如圖10所示，共有108個測量點。表3給出了對六分量測力數據的實驗數據不確定度。

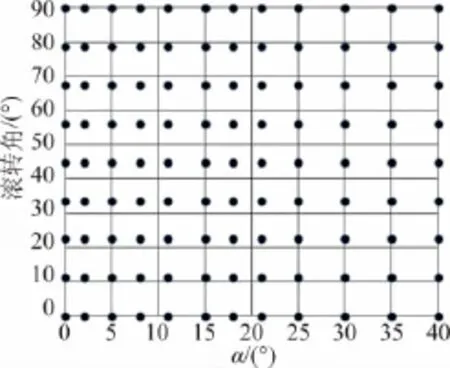
圖10 OFAT實驗的實驗測量點分布Fig.10 Distribution of the sample points in OFAT test

表3 實驗數據不確定度要求Table 3 Requirement of the uncertainty of the test data

4.2 形式試驗設計結果

初始樣本點為35點的均勻設計，增補了邊界點和重復點后最終設計為72個。樣本點組成為：初始均勻設計35個；角點4個；邊線點9個；重復點24個。

MDOE方法測量點要比OFAT方法的少36個點，測量點為OFAT方法的66.7%。為了增加大迎角下的測試點密度，迎角0°～12°范圍的樣本點在迎角方向間隔增加到1.2倍，最終設計如圖11所示。

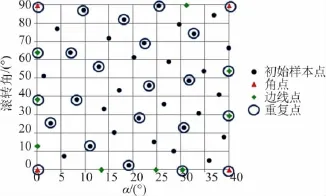
圖11 MDOE方法最終樣本點設計Fig.11 Final design of the sample points in MDOE test

4.2.1 實驗結果

通過“虛擬”風洞實驗獲得72個樣本點的六分量氣動力和力矩系數后對其進行建模，獲得圖12所示的響應面模型和不確定度評估。可以看出，利用均勻設計為基礎進行優化所得到的樣本點設計，擬合出的氣動響應面規律合理。盡管該模型的橫向氣動力和力矩系數表現出隨自變量強烈的非線性變化規律，樣本點對其非線性特征的采樣非常充分和準確。通過非參數建模的方式，能夠以非常直觀的形式表示出氣動特性隨迎角和滾轉角變化的規律，有利于分析和研究；而且以響應面模型給出風洞實驗結果，任意自變量組合的值都可以直接獲得，具有信息量大的優點。圖12右側一列給出了MDOE結果的不確定度，滿足實驗要求。

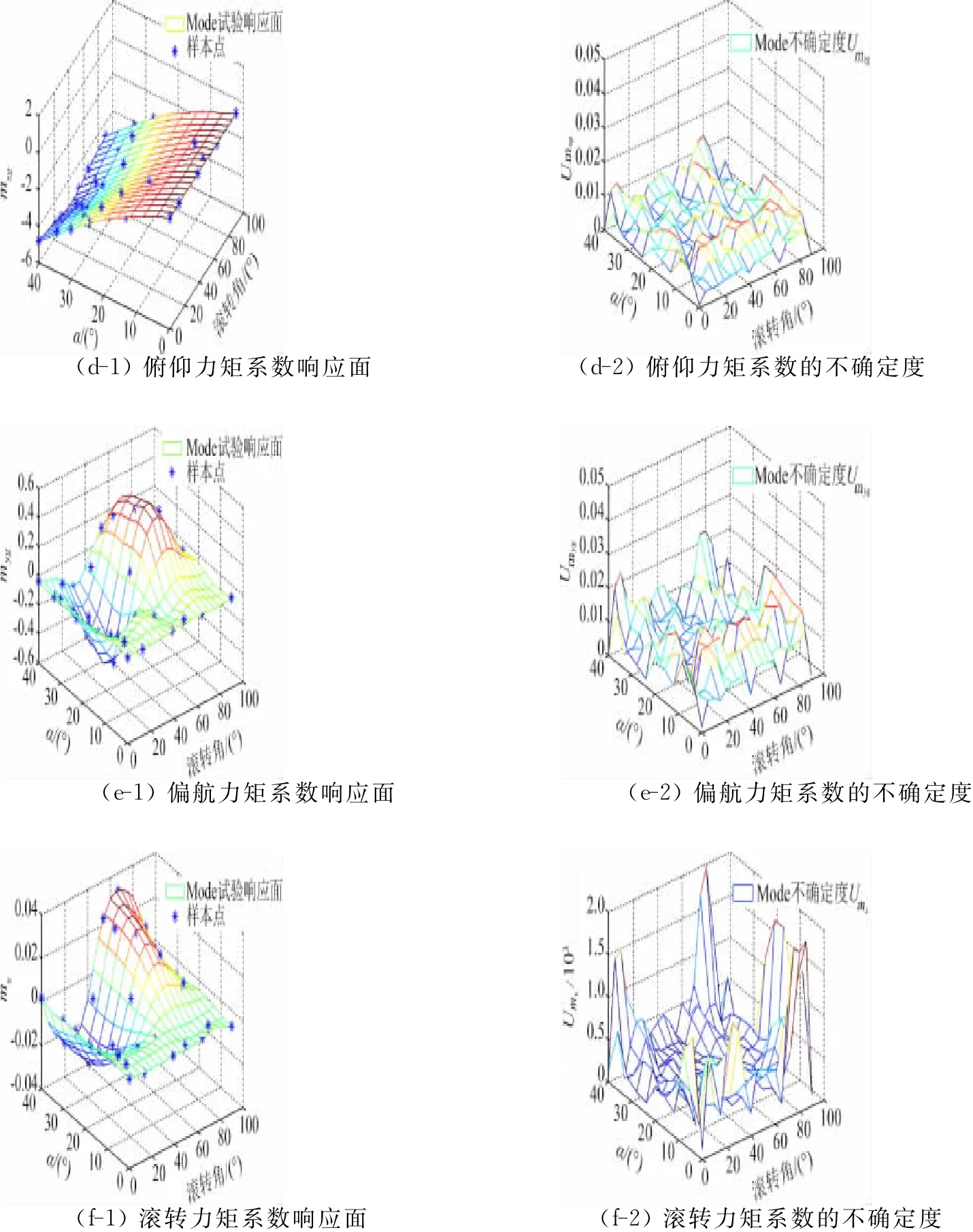
圖12 MDOE方法的六分量氣動力和力矩系數的響應面及不確定度Fig.12 Response surfaces and uncertainty of aerodynamic parameters in MDOE test

5 結 論

本文對風洞非參數模型MDOE的形式實驗設計方法進行了研究，對拉丁超立方設計和均勻設計應用于風洞實驗的適用性進行比較，并根據風洞實驗的特點發展幾種優化方法，主要結論有：

（1）對于風洞實驗均勻設計較拉丁超立方設計更為穩健、均勻，更適合基于非參數模型的風洞MDOE方法。

（2）在均勻設計方法基礎上，根據風洞實驗的特點發展了優化的方法，包括邊界點補充、樣本點密度調整和重復點設計，能夠將已有的“先驗信息”應用于實驗設計中。

（3）利用均勻設計為基礎進行優化所得到的樣本點設計，所需的測量點要少于OFAT方法的（如示例中所用的測量點數僅為OFAT方法的66.7%），且能夠充分和準確地對較劇烈的非線性變化規律進行采樣。

［1］ DeLoach R.Applications of modern experiment design to wind tunnel testing at NASA Langley research center［R］.AIAA 98－0713，36th AIAA Aerospace Sciences Meeting and Exhibit，Reno，NV，Jan.1998.

［2］ DeLoach R，Micol J R.Comparison of resource requirements for a wind tunnel test designed with conventional vs.modern design of experiments methods［R］.AIAA 2011－1260，49th AIAA Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition，Orlando，Florida，January 4－7，2011.

［3］ Box G E，Hunter W G，Hunter J S.Statistics for experimenters：an introduction to design，data analysis and model building［M］.1978.

［4］Drew Landman，Jim Simpson，Dan Vicroy，et al.Efficient methods for complex aircraft configuration aerodynamic characterization using response surface methodologies［J］.Journal of Aircraft，2007，44（4）：1189－1195.

［5］ 何為，薛衛東，唐斌.優化實驗設計方法及數據分析［M］.北京：化學工業出版社，2012.

［6］ Box G E，Hunter W G，Hunter J S.Statistics for experimenters：an introduction to design，data analysis and model building［M］.1978.

［7］ Richard DeLoach，Erickson Gary.Low－order response surface modeling of wind tunnel data over truncated inference subspaces［R］.AIAA 2003－0456，2003.

［8］ Erickson G E.Estimation of supersonic stage separation aerodynamics of winged－body launch vehicles using response surface methods［R］.NASA／TM－2010－216196，2010.

［9］ Ching F Lo，Zhao J L，DeLoach R.Application of neural networks to wind tunnel data response surface methods［R］.AIAA 2000－2639，2000.

［10］DeLoach R，Micol J R.Comparison of resource requirements for a wind tunnel test designed with conventional vs.modern design of experiments methods［R］.AIAA 2011－1260，49th AIAA Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition，Orlando，Florida，January 4－7，2011.

［11］Kai－Tai Fang，Runze Li，Agus Sudjianto.Design and modeling for computer experiments［M］.London：Taylor ＆Francis Group，LLC.

［12］王勁峰，姜成晟，李連發.空間抽樣與統計判斷［M］.北京：科學出版社，2009.

［13］方開泰.實驗設計與建模［M］.北京：高等教育出版社，2001.

［14］游海龍，賈新章，張小波，等.Kriging插值與拉丁超立方實驗相結合構造電路元模型［J］.系統仿真學報，2005，17（11）：2752－2755.

［15］方開泰.均勻設計與均勻設計表［M］.北京：科學出版社，1994.

［16］Fang K T，Wang Y.Number－theoretic methods in statistics［M］.Chaprrzanand Hall，London，1994.

［17］Hickernell F J.A generalized discrepancy and quadrature error bound［J］.Mathematics of Computation，1998，67：299－332.

Formal design of experiments method of MDOE in wind tunnel tests

Zhang Jiang＊，Qin Yongming，Ma Handong

（China Academy of Aerospace Aerodynamics，Beijing 100074，China）

The existing MDOE methods based on the parametric model cannot meet the tunnel test requirements of advanced vehicle because of strong nonlinear aerodynamic behaviors.It is necessary to develop the MDOE method based on the non－parametric model instead.The formal design of experiments method of MDOE for wind tunnel tests is researched in this paper.The applicability of Latin Hypercube Sampling and Uniform Design in wind tunnel tests is compared through virtual experiments.And several optimizing methods based on Uniform Design are devoleped，which can improve the quality of design results to meet the requirement of wind tunnel tests.Studies show that，Uniform Design is more robust and uniform than Latin Hypercube Sampling for the MDOE method based on the non－parametric model，the optimization including boundary complement，density adjustment of sampling points and repetition points design can utilize the priori information to the design，the formal design of experiments method developed in the paper requires less sampling points than the OFAT，which are only 66.7%in the demonstration，and samples the intensive non－linear changing law adequately and exactly.The studies on the formal design of experiments method of MDOE in wind tunnel tests laid the foundation for further study of the MDOE method based on the non－parametric model.

MDOE；non－parametric model；Uniform Design；Latin Hypercube Sampling；wind tunnel test

V211.74

Adoi：10.7638／kqdlxxb－2015.0116

0258－1825（2016）01－0059－11

2015－07－21；

2015－10－25

張江＊（1978－），男，陜西綏德，高工，博士，研究方向：實驗流體力學.E－mail：13611319903＠163.com

張江，秦永明，馬漢東.風洞MDOE的形式實驗設計方法研究［J］.空氣動力學學報，2016，34（1）：59－69.

10.7638／kqdlxxb－2015.0116 Zhang J，Qin Y M，Ma H D.Formal design of experiments method of MDOE in wind tunnel tests［J］.Acta Aerodynamica Sinica，2016，34（1）：59－69.