基于ANSYS/LS-DYNA的鋼筋剪切過程的數值模擬

徐賀偉，盧秀春，楊榮剛，王 鍵，楊慧杰

(燕山大學 機械工程學院，河北 秦皇島 066004)

基于ANSYS/LS-DYNA的鋼筋剪切過程的數值模擬

徐賀偉，盧秀春，楊榮剛，王 鍵，楊慧杰

(燕山大學 機械工程學院，河北 秦皇島 066004)

剪切刀具是鋼筋剪切機的核心部件，是剪切機研究的重要部分。分析鋼筋剪切過程中的彈、塑性變形及斷裂機理，簡述鋼筋剪切時剪切力的理論計算公式，以某廠鋼筋隨動剪切機剪切刀具為參考，建立鋼筋剪切有限元模型，對剪切過程進行動力學仿真，分析參數對剪切力的影響，并用實驗驗證仿真結果的正確性，得出如下結果：增大上、下切刀側向間隙，剪切力先減小后增大，側向間隙為0.1 mm時，剪切力最小；增大上切刀刀刃傾角，剪切力減小。研究結果可為剪切機刀具設計與實驗設備的安裝調試提供理論依據。

鋼筋剪切；有限元模型；剪切力

0 前言

鋼筋切斷機廣泛應用于鐵路、建筑、機械制造等行業，盤料供貨的鋼筋需要對其進行剪切獲得所需長度。隨著科技的進步，現有鋼筋剪切機的性能已不能適應用戶的需求，還需對其進行深入研究，使剪切機達到更好的使用性能[1]。

由于生產的需要，使得鋼筋切斷機得到迅速發展，許多學者對其進行了研究。文獻[2]對鋼筋剪切過程進行了動態仿真，分析了剪切過程中剪切力的變化規律，得到鋼筋模型被剪斷時的應力、應變動態分布規律；文獻[3]對圓盤剪剪切力計算公式進行討論，并得到剪切過程中銅板的應力應變狀態及剪切力變化曲線；文獻[4]推導了斜刃剪切的刀刃曲線方程，得出斜刃剪切時剪切力比平刃剪切時小的結論。

目前，學者們只對鋼筋剪切時剪切力變化進行了動態檢測，并未研究上下切刀間隙、切刀刀刃傾角等參數對剪切力變化規律的影響。本文的主要工作是建立鋼筋剪切模型，用有限元軟件對剪切過程進行模擬，對剪切過程中的應變及剪切力進行分析，研究上下切刀側向安裝間隙、上切刀刀刃傾角的變化對剪切力變化規律的影響，并用實驗驗證模擬結果的可靠性，為鋼筋剪切機刀具的安裝及刀具的設計提供參考。

1 剪切力理論公式計算

鋼筋剪切過程分為四個階段：第一階段為鋼筋的彈性變形階段，開始剪切時上、下切刀對鋼筋的擠壓應力還沒有達到鋼筋的彈性極限，此時應力應變成正比，當切刀的擠壓應力消失時，鋼筋變形消失；第二階段為鋼筋的塑性變形階段，隨著剪切的進行，當刀具對鋼筋的擠壓應力大于鋼筋的彈性極限時，鋼筋發生不可恢復的塑性變形；第三階段為鋼筋的撕裂階段，當上切刀繼續施加對鋼筋的縱向剪切時，鋼筋的變形越來越大，鋼筋的變形抗力越來越大，此時鋼筋的受剪面積隨著變形程度的加大而減小，所以鋼筋單位面積所受到的剪切應力增大，當剪切應力達到剪切強度時，剪切面晶粒發生錯位，在與刀片接觸兩端出現剪切裂紋；第四階段為斷裂階段，動刀片繼續剪切，第三階段出現的裂紋擴大最后斷裂，剪切結束[5-7]。

鋼筋剪切過程是一個復雜的過程，目前為止，剪切力沒有一個精確的計算公式。實驗過程中取PC鋼棒直徑為10 mm，強度極限為460 MPa，鋼筋進給速度為60 m/min。在工程實際應用中[8]，剪切力大小采用如下公式計算

Pmax=K1K2Aσb

(1)

式中，K1為剪刃磨鈍系數，一般取K1=1.2左右；K2為抗剪極限強度與抗拉極限強度之比，一般取K2=0.6左右；A為鋼棒橫截面面積，mm2； 為材料強度極限，MPa。

2 有限元模擬

2.1 剪切模型的建立

以某廠鋼筋隨動剪切機刀具為參考，建立剪切有限元模型，如圖1所示。上切刀如圖2所示，刃口設計成具有一定半徑的圓弧，刀刃沿厚度方向有一定傾角。剪切過程中下切刀固定不動，上切刀在液壓裝置的帶動下在垂直方向對鋼筋進行剪切，剪切結束上切刀回到初始位置。

模擬過程中，鋼筋材料選取為Q235，參數值見表1。上、下切刀定義為剛體，切刀材料密度7 860 kg/m3;彈性模量2.07×105MPa;泊松比0.3。上、下切刀和鋼筋選取單元類型為SOLID164，切刀采用自由網格劃分，鋼筋采用映射網格劃分，對鋼筋剪切區域進行網格細化；仿真過程中，上、下切刀與鋼筋接觸類型定義為自動面面接觸(ASTS)，ASTS為雙向接觸。模擬過程中，雙向接觸即檢查主面節點對從面的穿透，又檢查從面節點對主面的穿透，從而定義了整個剪切過程中的各個接觸；對下切刀所有自由度進行約束，上切刀約束所有旋轉自由度和X、Z方向移動自由度，對鋼筋軸線約束繞X軸旋轉自由度；給上切刀沿Y軸負方向的初速度1.2 m/s，計算時間設置為0.01 s。

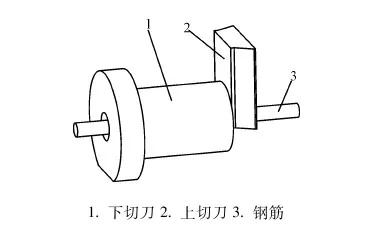
1.下切刀 2.上切刀 3.鋼筋圖1 剪切模型Fig.1 Model of cutting

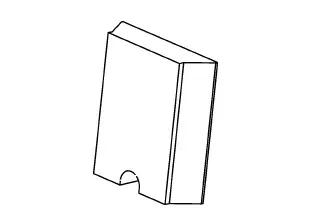
圖2 上切刀Fig.2 Upper cutter

參數數值密度/kg·m-37810彈性模量/Pa2.1×1011泊松比0.261屈服應力/Pa2.6×108切線模量/Pa5.84×108硬化參數1應變速率40影響系數5失效應變0.4

2.2 有限元模擬結果

取直徑為10 mm的鋼筋對剪切過程進行模擬，模擬時上、下刀片間側向間隙取0.1 mm，上刀片刀刃傾角取3°。

圖3為剪切開始與剪切結束時刻鋼筋塑性應變分布圖，從圖中可以看出，距離切口越近處塑性應變越大，沿著切口向外塑性應變逐漸減小。參數設置過程中設置的失效應變為0.4，而剪切結束應變圖中塑性應變最大值為0.3999，比設定值偏小，產生此種現象的原因為有限元仿真中使用單元失效法，剪切過程中失效單元被刪除。

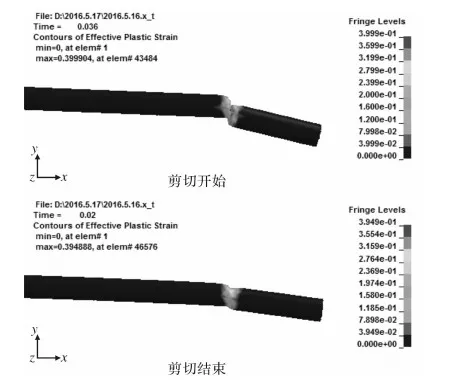
圖3 剪切鋼筋塑性應變圖Fig.3 Diagram of plastic strain during cutting steel bar

圖4為整個剪切過程中剪力變化曲線，此模擬過程與文獻[9]及文獻[10]所得剪切力變化規律一致。從上切刀接觸到鋼筋開始，隨著上切刀切入深度的增加，剪切力逐漸增大，當上切刀剪切一定深度時(此深度與被剪切鋼筋抗拉強度等參數有關)，剪切力達到最大值，鋼筋變形轉為滑移階段，剪切力逐漸變小。

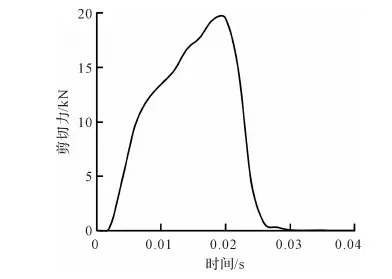
圖4 剪切力曲線Fig.4 Curve of cutting force

2.3 參數對剪切力的影響分析

側向間隙是指上、下刀片沿鋼筋軸線方向的安裝距離，側向間隙過小，可能導致剪切時上刀片與下刀片產生摩擦，刀片磨損加快，影響剪切進行；側向間隙過大，將引起剪切時鋼筋的震動，影響剪切斷面質量，使斷面毛刺增多，對剪切精度產生一定影響。

上、下切刀側向間隙的變化對剪切力的影響如圖5所示，剪切力隨刀具側向間隙的增加先減小后增大；側向間隙為0.1 mm時，鋼筋剪切力最小，此時剪切力為19.55 kN；側向間隙在0.2～0.3 mm之間時，剪切力增大速率較快。

圖5 上下切刀軸向間隙對剪切力影響Fig.5 Effect of axial gap between upper and lower cutter on cutting force

上切刀刀刃沿厚度方向傾角的大小對剪切力有一定影響，傾角過小不利于鋼筋剪切，不能保證鋼筋剪切面的質量；傾角過大使刀具磨損加快，頻繁更換刀具影響生產效率。

上切刀刀刃傾角對剪切力的影響如圖6所示，實驗時取上、下切刀側向安裝間隙為0.1 mm。由圖可見，剪切力隨著上切刀刀刃傾角的增大逐漸減小，刀刃傾角小于3°時，剪切力變化較快；刃傾角大于3°小于4°時，剪切力基本不變。

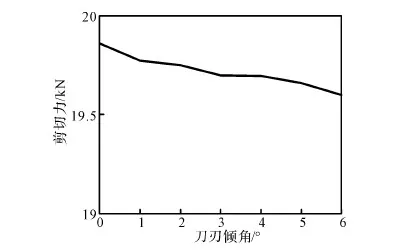
圖6 上切刀刀刃傾角對剪切力影響Fig.6 Effect of upper cutter edge angle on cutting force

3 模擬與實驗對比分析

采用實驗方法對仿真結果可靠性進行驗證，實驗使用的儀器為燕山大學軋制中心為某企業生產的鋼筋隨動剪切機，在上切刀上粘貼電阻式應變片對剪切力進行測量，電阻應變片將應變轉化為電阻的變化，利用電橋將電阻變化轉變為電壓變化，將信號送入放大器，利用標定曲線推算出剪切力大小。實驗時取上切刀刀刃傾角為3°，實驗所用鋼筋隨動剪切機與剪切鋼筋如圖7所示。

圖7 隨動剪切機及剪切鋼筋Fig.7 Cutting machine and steel bar

表2為上、下切刀在不同側向間隙下鋼筋剪切力實驗與仿真結果對比，實驗數據的獲得是在同一參數下進行五次實驗，將剪切力取五次實驗平均值。由表中數據得出，實驗結果均大于仿真結果，出現這種現象的原因是仿真時沒有考慮鋼筋形變及外界條件等因素的影響。實驗所得剪切力隨上、下切刀側向間隙變化規律也是先增大后減小，與有限元模擬結果相同；實驗剪切力與仿真所得剪切力誤差在7%以內，此值在合理范圍內，實驗驗證了仿真結果的可靠性。

表2 剪切力實驗與仿真結果

4 結論

以某企業鋼筋隨動剪切機的刀具為建模依據，建立鋼筋剪切模型，對剪切力進行理論公式計算，用有限元軟件對鋼筋剪切過程進行模擬，研究參數對剪切力的影響規律，并用實驗驗證仿真結果的正確性。結果表明：鋼筋剪切力是一個先增大后減小的漸變過程。上、下切刀側向間隙增大，剪切力先減小后增大，側向間隙為0.1 mm時剪切力最小；剪切力隨上切刀刀刃傾角的增大而減小；實驗所得剪切力隨上、下切刀側向間隙的變化規律與仿真結果一致，且實驗誤差與仿真誤差在合理范圍內，驗證了仿真結果的可靠性。研究結果為鋼筋剪切機刀具的安裝及刀具的結構優化提供理論基礎。

[1] 孟進禮, 衛青珍. 對鋼筋切斷機發展的幾點看法[J]. 建筑機械化, 2000,21(5): 14-15.

[2] 劉中, 朱振華, 衛青珍. 基于LS-DYNA 的鋼筋切斷機剪切鋼筋的動態仿真[J]. 太原科技大學學報, 2011,32(1):33-36.

[3] 戴志凱, 許 平, 張寶勇, 等. 基于LS-DYNA的分條圓盤剪切力的計算研究[J]. 新技術新工藝, 2013:69-71.

[4] 孟 凡, 李郝林.基于ANSYS/LS-DYNA的碎邊剪切力計算研究[J]. 機械工程與自動化, 2015(2):45-47.

[5] 王伯平. 鋼筋切斷機切斷鋼筋的機理分析[J]. 建筑機械化，1988,9(7): 20-22.

[6] 章友文. 鋼筋切斷機剪切機理分析[J]. 工程機械，1991, 22(3): 16-19.

[7] 劉鴻鷹. 鋼筋剪切塑變理論分析[J]. 建筑機械化，1996, (2): 8-10.

[8] 楊中鋒. 凸輪擺桿剪切系統研究及性能分析[D]. 秦皇島: 燕山大學，2013.

[9] 段紅杰, 陶 浩. 鋼筋切斷機動力學仿真設計[J]. 制造業自動化, 2010, 32(4): 143-145.

[10]陶 浩, 段紅杰. 鋼筋切斷機的動力學性能[J]. 煤礦機械， 2008, 28(5): 81-83.

Numerical simulation of steel bar shearing process based on ANSYS/LS-DYNA

XU He-wei, LU Xiu-chun, YANG Rong-gang, WANG Jian, YANG Hui-jie

(College of Mechanical Engineer, Yanshan University, Qinhuangdao 066004, China)

Cutter is an important part of steel bar cutting machine. The elastic-plastic deformation and fracture mechanism of steel bar are analyzed during cutting. Cutting formula is listed. Cutting model is found based on a factory’s steel bar cutting machine. Dynamics simulation of cutting process is done, and parameters influence on cutting force are analyzed, and the reliability of simulation results is verified by experiments. A series of simulation results are obtained. Cutting force is decreasing first and then increasing with the increase of side gap between upper and lower cutter, and cutting force is the smallest when the distance is 0.1mm. Cutting force is decreasing with the cutting edge angle increase of upper cutter. The results provides theoretical basis for the cutting machine design and installation.

steel bar shearing; finite element model; cutting force

2016-05-25；

2016-07-12

徐賀偉(1990-)，女，燕山大學機械工程學院，碩士研究生。

盧秀春(1954-)，男，燕山大學機械工程學院教授，研究方向：機械設計及理論。

TG333.2+1

A

1001-196X(2016)06-0021-04