基于相關性的小波熵心電信號去噪算法

王曉燕，魯華祥,2，金敏，龔國良，毛文宇，陳剛

(1. 中國科學院 半導體研究所，北京 100083； 2. 中國科學院 腦科學與智能技術卓越創新中心，上海 200031)

基于相關性的小波熵心電信號去噪算法

王曉燕1，魯華祥1,2，金敏1，龔國良1，毛文宇1，陳剛1

(1. 中國科學院 半導體研究所，北京 100083； 2. 中國科學院 腦科學與智能技術卓越創新中心，上海 200031)

針對心電信號的基線漂移、工頻噪聲、肌電噪聲，本文提出了基于相關性的小波熵去噪算法。算法首先根據基線漂移的低頻特性，確定小波分解的層數，置零近似系數，去除基線漂移；再對相鄰尺度的高頻小波系數進行相關處理，依據小波熵自適應地計算全局閾值去除工頻和肌電噪聲；最后將置零的近似系數和閾值處理后的小波系數重構得到有效信號。該算法能夠在一次小波分解、重構的過程中，同時濾除心電信號中的3種主要噪聲。對MIT-BIH數據庫數據和模擬數據的仿真實驗結果也表明該算法的去噪效果顯著優于其他算法。

心電信號；去噪；相關性；小波熵；自適應

心電信號是心臟電活動在體表的綜合表現，心電信號診斷因可靠、簡便、對患者無創等優點，臨床應用十分廣泛。然而心電信號在測量時不可避免地存在一些強干擾和噪聲，如基線漂移、工頻噪聲、肌電噪聲和環境噪聲等[1]。如何有效排除各種噪聲，準確提取出有用的心電信號波形，是臨床心臟病智能診斷的重要基礎。

心電信號的頻率在0.05～100 Hz之間，其中90%的能量集中在0.25～35 Hz之間。而心電信號噪聲主要有50 Hz/60 Hz及其諧波組成的工頻干擾、5～2k Hz的肌電干擾以及頻率小于0.5 Hz的基線漂移等[2]。目前常用的方法主要有形態學濾波法[3]、EMD分解法[4]、基于小波理論的小波閾值法[5-7]、小波熵閾值去噪法[8]以及相關方法的結合[9-10]等。形態學濾波法處理基線漂移效果完美，但處理高頻噪聲會產生階段誤差。基于EMD分解法能夠對信號自適應地從高頻到低頻分解為固有模態函數，根據噪聲一般分布的頻段，直接舍棄某些高頻分量和低頻分量，在去掉噪聲的同時也會去掉一部分原始信號。小波變換是一種信號的時間-頻率分析方法，具有多分辨率的特征，去除心電噪聲效果顯著。小波閾值去噪法在計算噪聲方差時，通常將最高一層高頻小波系數看作噪聲，求取其作為噪聲方差，具有一定誤差。文獻[8]中的基于小波熵的去噪法，對高頻小波系數進行處理，高頻噪聲去除效果良好，但忽略了低頻近似系數的影響，基線漂移去除效果不理想。

針對以上問題，本文提出一種基于相關性的小波熵心電信號去噪方法。首先對信號進行小波分解，對基線漂移，通過置零近似系數去除；對肌電噪聲和工頻噪聲，需要在高頻小波系數中對信號和噪聲進行區分，利用各尺度間有效信號和噪聲相關性不同的特性，對高頻小波系數進行相關性處理，將有效信號和噪聲分離，從而利用噪聲計算小波熵閾值。最后將置零的近似系數和各尺度閾值處理后的高頻系數進行重構，得到去噪信號。算法充分利用不同類型的噪聲特性，能夠在一次小波分解、重構的過程中同時濾除心電信號的3種主要噪聲，且根據信號能量自適應地選取閾值的方式，能夠在提高信噪比的同時更好地保護有效信號。本文最后利用MIT-BIH標準心電數據庫等檢驗了所提算法，仿真實驗結果表明，算法復雜度低，且去噪效果顯著優于目前典型的心電去噪算法。

1 小波閾值去噪算法

假設含噪信號由式(1)表示：

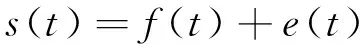
(1)

式中：t為時間序列，t=1,2,…,N，s(t)為含噪信號；f(t)為原始信號，e(t)為噪聲。

小波變換是一種信號的多尺度分析方法，離散小波分解通過Mallet算法[11]實現，如式(2)。

(2)

式中：s(t)為原始信號；j為分解層數；H、G為小波分解濾波器系數；Aj為信號在層的近似部分(即低頻部分)的近似系數；Wj為信號s(t)在第j層的細節系數(即高頻部分)的小波系數。

小波去噪的根本任務是在小波域將信號的小波變換與噪聲的小波變換有效地分離。由于有效信號分解后的小波系數絕對值比較大，而噪聲信號的能量相對分散，表現為小波分解后的小波系數絕對值較小，因此可以通過閾值處理方法進行去噪。當小波變換系數小于閾值時，認為主要由噪聲引起，予以舍棄；當小波系數大于閾值時，認為主要由信號引起，予以保留；然后用新的近似系數和小波系數進行重構得到去噪后的信號。

信號與噪聲的分離關鍵在于閾值的選擇，Donoho提出的閾值計算公式如式(3)所示：

(3)

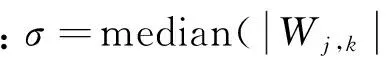
2 基于相關性的小波熵閾值去噪算法

2.1 算法的基本思想

對含噪信號進行小波分解后得到低頻近似系數和高頻小波系數。一般將低于0.5Hz的低頻分量看作基線漂移，為去除基線漂移，算法根據基線漂移的低頻特性來確定小波分解的層數，使分解得到的最低頻的近似系數的頻率范圍接近基線漂移的頻率范圍, 再將最低頻的近似系數置零即去掉基線漂移。

工頻和肌電噪聲和心電信號頻譜有重疊，需要在高頻小波系數中進行處理。根據有效信號的小波系數在各尺度間具有較強的相關性，而噪聲的小波系數在各尺度間無明顯的相關性，可以區分有效信號和噪聲。對高頻小波系數進行相關性分析，確定噪聲夾雜的有效信號的位置，并將這些有效信號置零；設置噪聲能量閾值，循環多次剔除有效信號從而得到各尺度新的高頻小波系數。如果忽略對高頻小波系數的相關性處理工作，在去噪過程中會因為未有效區分噪聲，導致有效信號損失。小波熵作為小波變換與信息熵的結合，可以在時頻域上對信息的能量做出度量[12]。將經過相關性分析的高頻小波系數等分為若干區間，計算各區間的小波熵值，選取最大小波熵值子區間的高頻小波系數平均值的絕對值作為噪聲方差。這種方法在一定程度上減少了閾值選取的盲目性。

2.2 相關性計算

相關系數計算公式如式(4)所示：

(4)

式中：Cj,k為分解尺度j上k點的相關系數，Wj,k和Wj+1,k分別為尺度j和尺度j+1上k點的小波系數。

為使相關系數與小波系數具有可比性，需要定義規范化相關系數[13]，定義(5)為Cj,k的規范化相關系數：

(5)

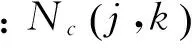
顯然，在尺度j下，小波系數Wj,k與規范化相關系數具有相同的能量，這為它們之間提供了可比性。記錄各尺度規范化相關系數大于高頻小波系數的位置，該位置即為各尺度高頻小波系數中有效信號的位置，并將該位置的高頻小波系數置零，得到新的高頻小波系數，認為其全部是由噪聲引起的，由這些系數計算噪聲方差。

2.3 小波熵

對信號進行l尺度分解，設尺度j上的小波系數為Wj=(Wj,1,Wj,2,…,Wj,N)。若小波基函數為正交基，尺度j的小波變換滿足能量守恒原則。因此，尺度j的小波能量Ej等于該尺度小波系數的平方和，如式(6)所示 ：

(6)

式中N為采樣點數。信號的總能量計算公式如式(7)所示：

(7)

由式(6)和式(7)可以確定第j層小波系數的信號能量在總能量中存在的概率為

(8)

已知概率，可以確定信號小波熵S[15]為

(9)

2.4 閾值處理

本文提出的噪聲方差計算公式如式(10)：

(10)

采用的閾值處理函數如式(11)：

(11)

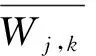
2.5 算法流程

1)根據基線漂移的低頻特性設置小波分解層數，對含噪信號進行多尺度分解，得到最低頻的近似系數和各尺度高頻小波系數。

2)將低頻近似系數置零，去除基線漂移。

3)選取有限個樣本的方差作為初始噪聲的方差[14]，這里采用最高頻小波系數的前80個點估計初始噪聲，計算方差sigma1，設置閾值k。

4)將相鄰尺度的高頻小波系數進行相關性計算，將系數大于規范化系數的位置上的小波系數置零，剩下的為噪聲產生的系數，從而估計噪聲方差sigma2。

5)若sigma2>k·sigma1，返回4)，否則，利用sigma2和小波熵計算全局閾值。

6)對每一層的高頻小波系數利用全局閾值進行處理。并將新低頻近似系數和新高頻小波系數進行重構，得到去噪后的信號。

3 數據仿真與實驗結果

本文在IntelCorei5-3470CPU+4G內存的計算機平臺上，使MATLAB軟件編程實現對信號的仿真實驗，選取的小波函數為bior3.7小波。

3.1 數據來源和評價標準

實驗針對心電信號進行定性和定量仿真實驗。定性實驗數據采用來自MIT-BIH[16]心律失常數據庫(ArrhythmiaDatabase)和MIT-BIH噪聲數據庫(即NstdbDatabase)中真實的心電數據。定量實驗為方便計算，利用MATLAB模擬干凈的心電信號。

本文的方法是在分析小波系數相鄰尺度相關性和小波熵的基礎上提出來的，為了驗證所提算法的優越性，使用信噪比(SNR)、均方根誤差(MSE)和運行時間T3個指標來進行衡量和比較。信噪比和均方根誤差公式如式(12)、(13)：

(12)

(13)

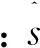
3.2 對心律失常數據庫信號去噪

MIT-BIH心律失常數據庫(ArrhythmiaDatabase)中的心電數據含噪聲較少，選取其100號數據的前2 048個數據作為本次研究的信號，人為加入工頻干擾、基線漂移和高頻噪聲(包括肌電干擾)3種噪聲。基線漂移、工頻干擾和高頻噪聲分別來自MIT-BIH噪聲數據庫(NstdbDatabase)中的bw、em和ma數據。本文算法與改進的小波閾值算法[1]和小波熵去噪算法[8]對比，以輸入信噪比為-2.6dB、均方誤差為0.253 9為例，去噪效果如圖1～5所示，為方便觀察基線漂移，顯示前6個周期。

(a)原始信號波形圖

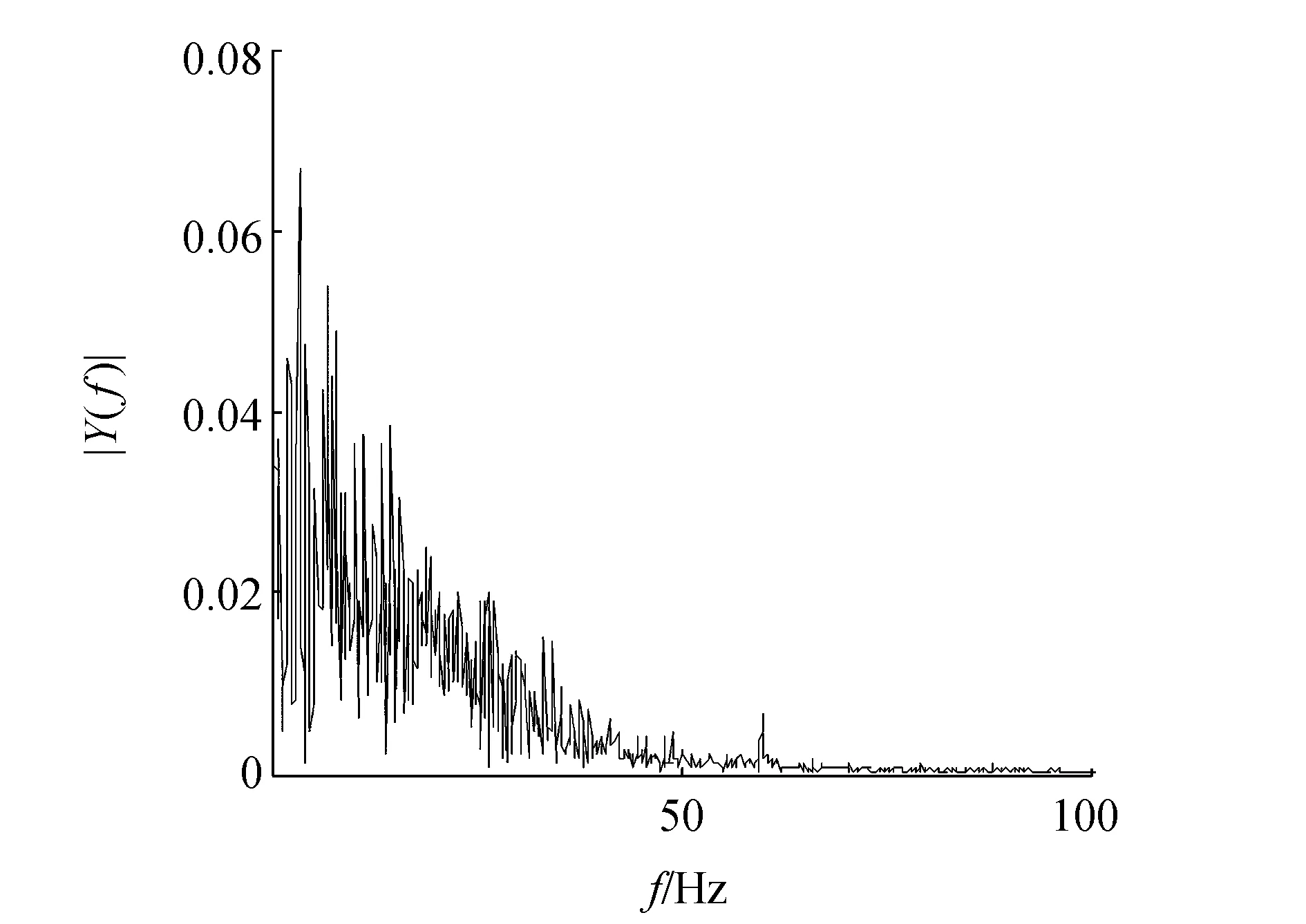
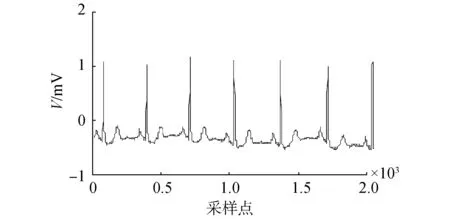
(b)原始信號頻譜圖圖1 原始信號波形及頻譜圖Fig.1 The waveform and spectrum of original signals

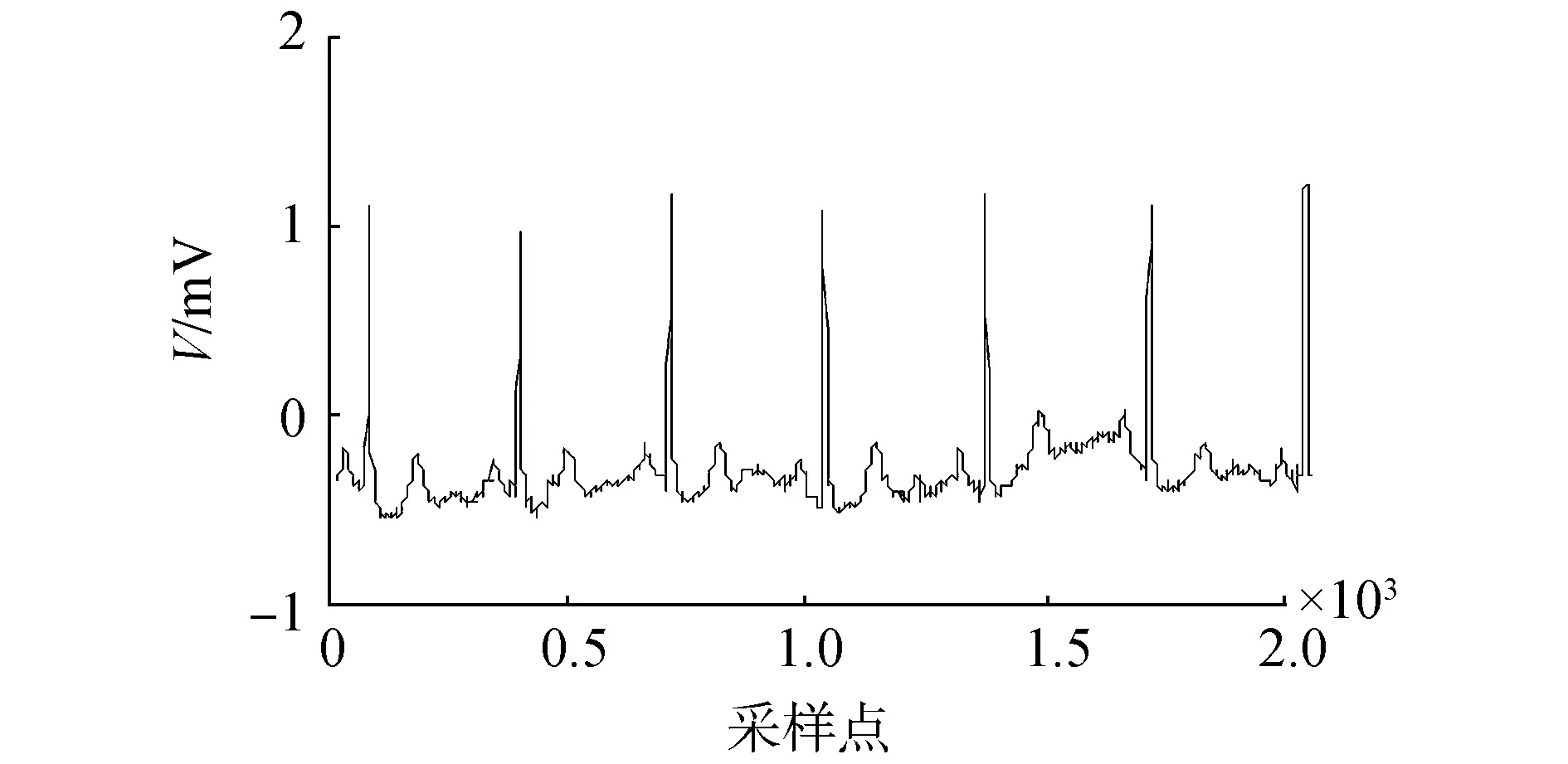
(a)加噪信號波形圖

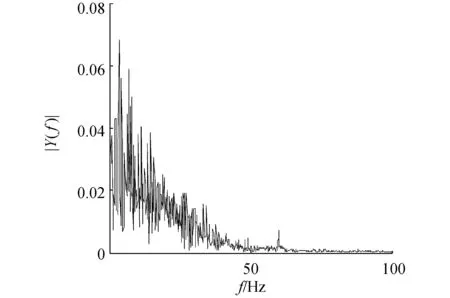
(b)加噪信號頻譜圖圖2 加噪信號波形及頻譜圖Fig.2 The waveform and spectrum of noisy signals

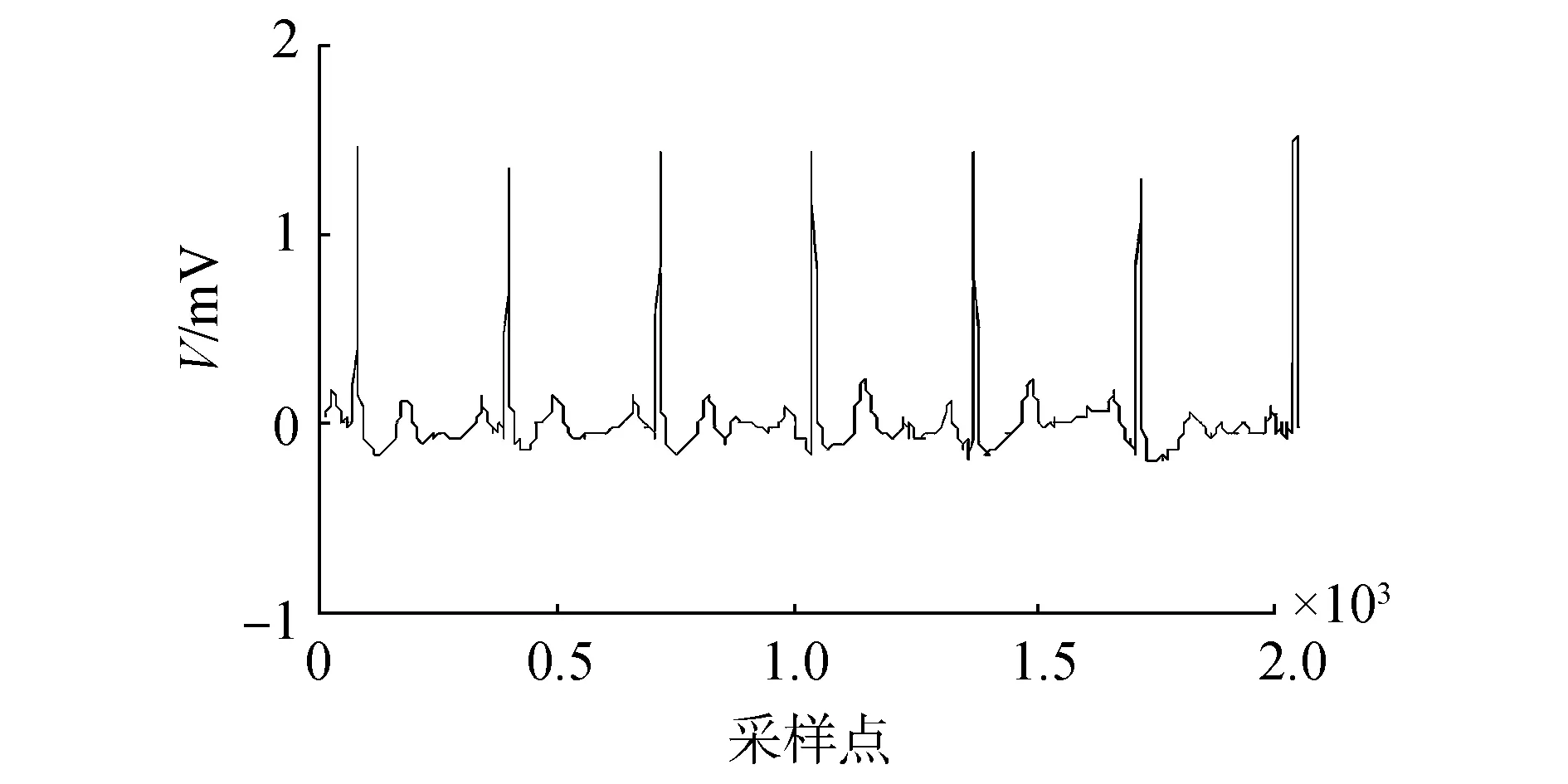
(a)改進的小波閾值算法去噪波形圖

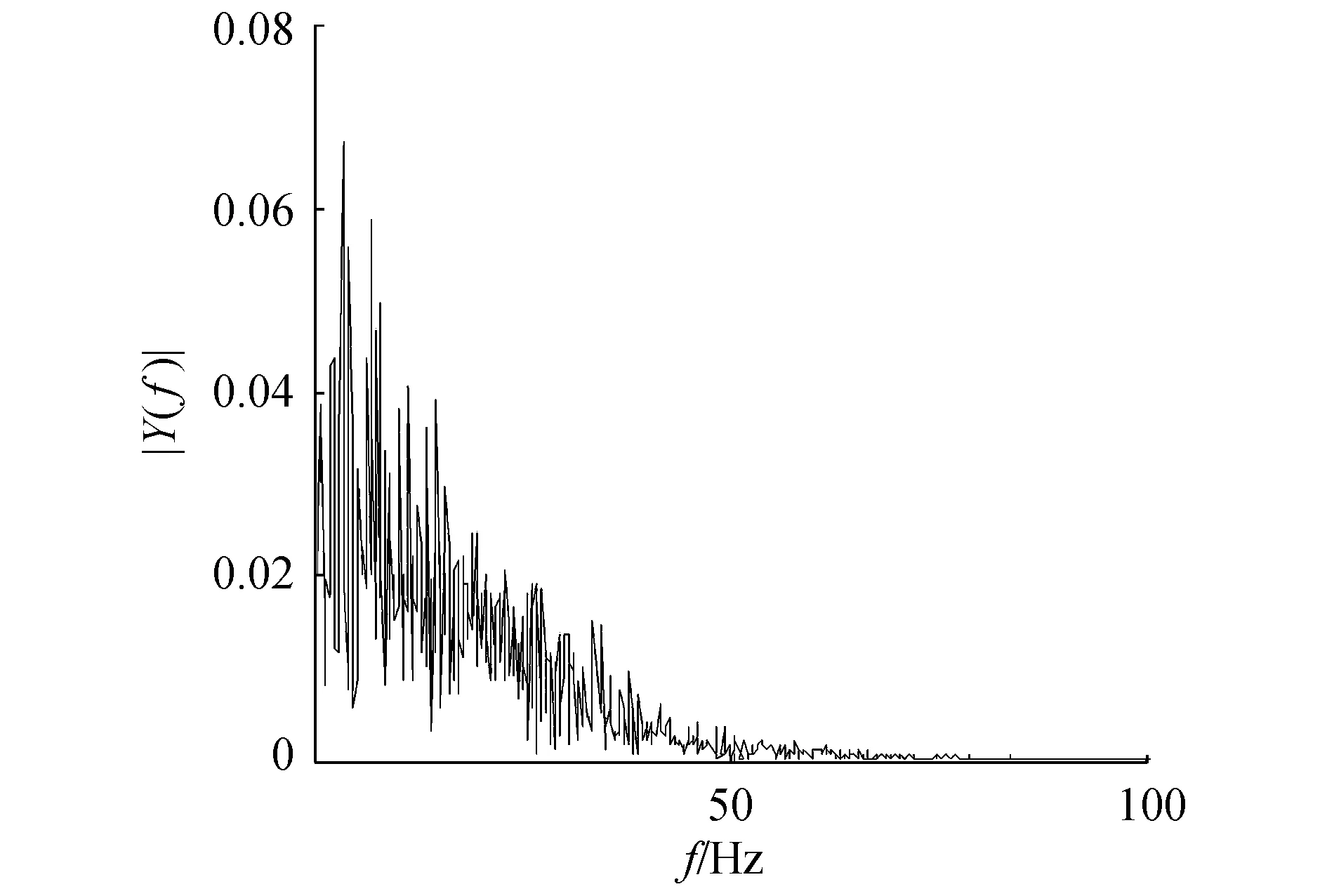
(b)改進的小波閾值算法去噪頻譜圖圖3 改進的小波閾值算法去噪波形及頻譜圖Fig.3 The waveform and spectrum of de-nosing signals of improved wavelet threshold algorithm

(a)小波熵算法去噪波形圖

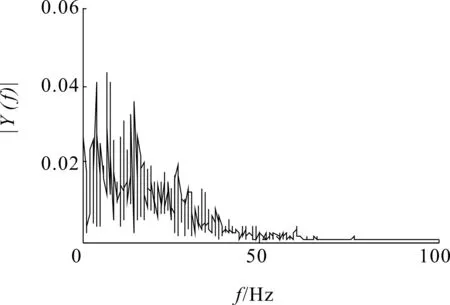
(b)小波熵算法去噪頻譜圖圖4 小波熵算法去噪波形及頻譜圖Fig.4 The waveform and spectrum of de-nosing signals of wavelet entropy algorithm

(a)本文算法去噪波形圖

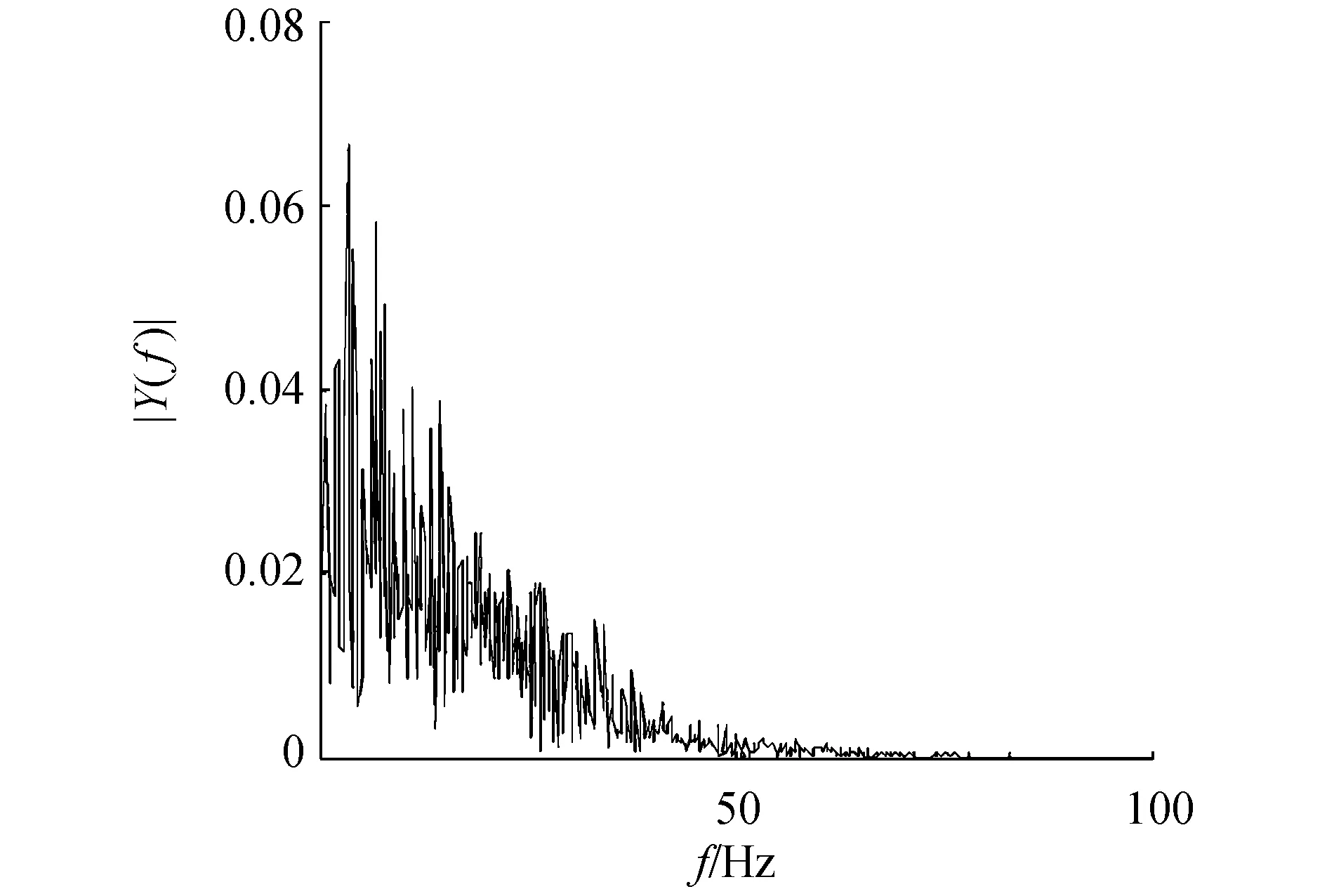
(b)本文算法去噪頻譜圖圖5 本文算法去噪波形及頻譜圖Fig.5 The waveform and spectrum of de-nosing signals of proposed algorithm

該數據庫中工頻噪聲主要集中在60Hz左右。可以看出，本文提出的基于相關性的小波熵去噪算法與目前兩種典型的心電信號去噪算法相比，基線漂移、60Hz工頻干擾被很好地去除；波形連續性強，無震蕩現象，波形清晰完整，去除肌電噪聲效果顯著。即可以在一次小波分解、重構的過程中同時去除3種主要的心電信號噪聲。

3.3 對噪聲數據庫信號去噪

MIT-BIH噪聲數據庫(NstdbDatabase)是真實的帶噪聲的信號，對該數據庫中118e06信號的前2 048個數據分別用3種去噪算進行去噪，結果如圖6～9所示，為方便觀察波形，對比去噪效果，波形只顯示3個周期。

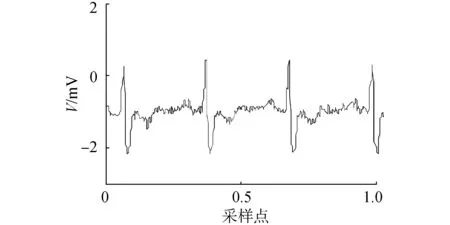
(a)含噪信號波形圖

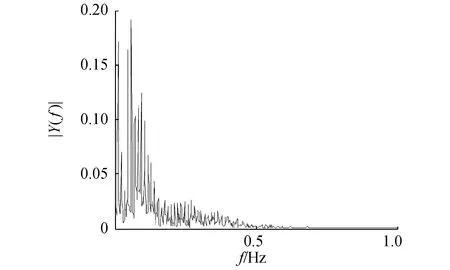
(b)含噪信號頻譜圖圖6 含噪信號波形及頻譜圖Fig.6 The waveform and spectrum of noisy signals

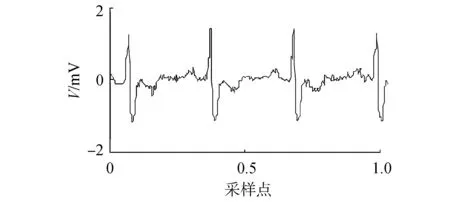
(a)改進的小波閾值算法去噪波形圖

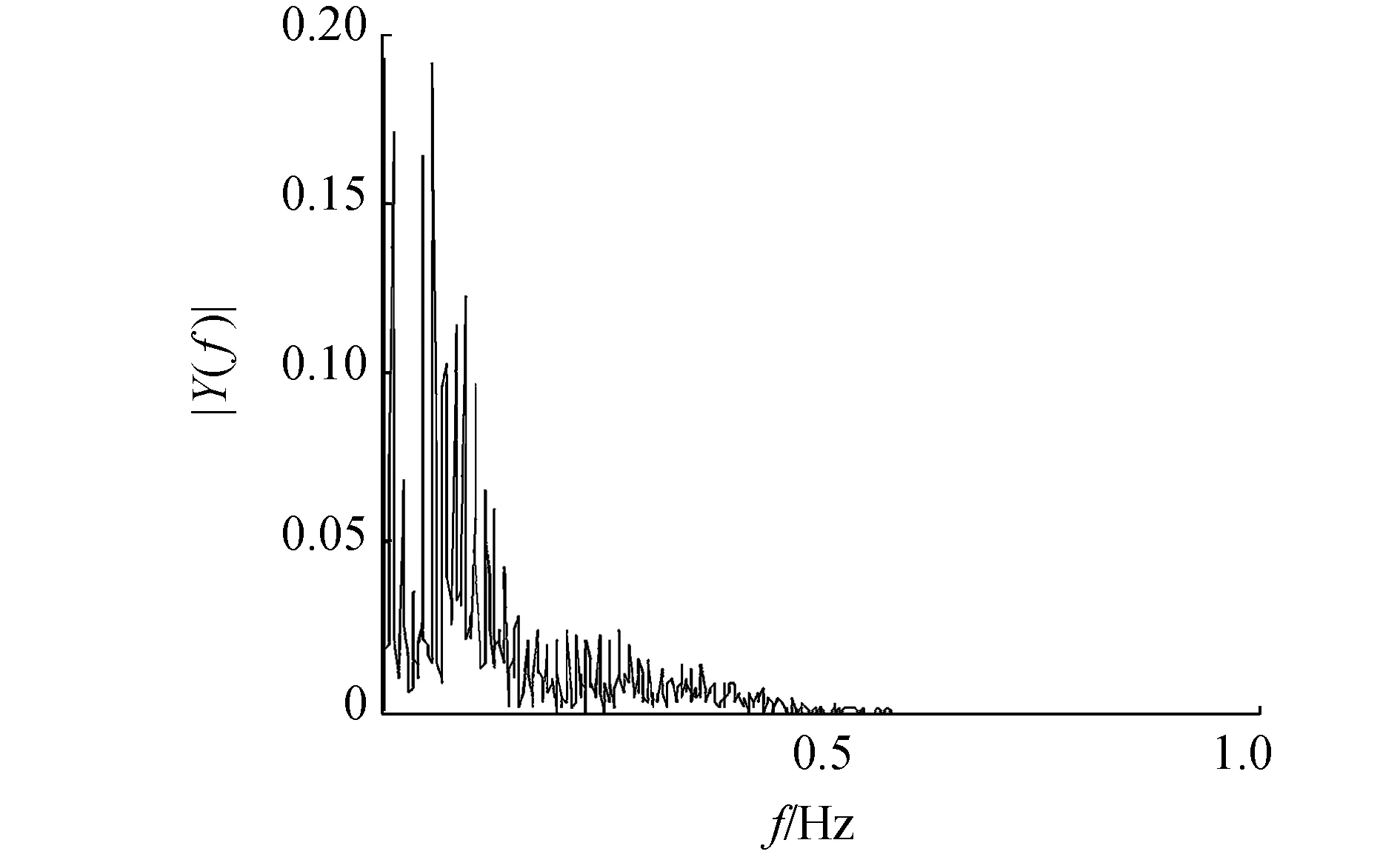
(b)改進的小波閾值算法去噪頻譜圖圖7 改進的小波閾值算法去噪波形及頻譜圖Fig.7 The waveform and spectrum of de-nosing signals of developed wavelet threshold algorithm

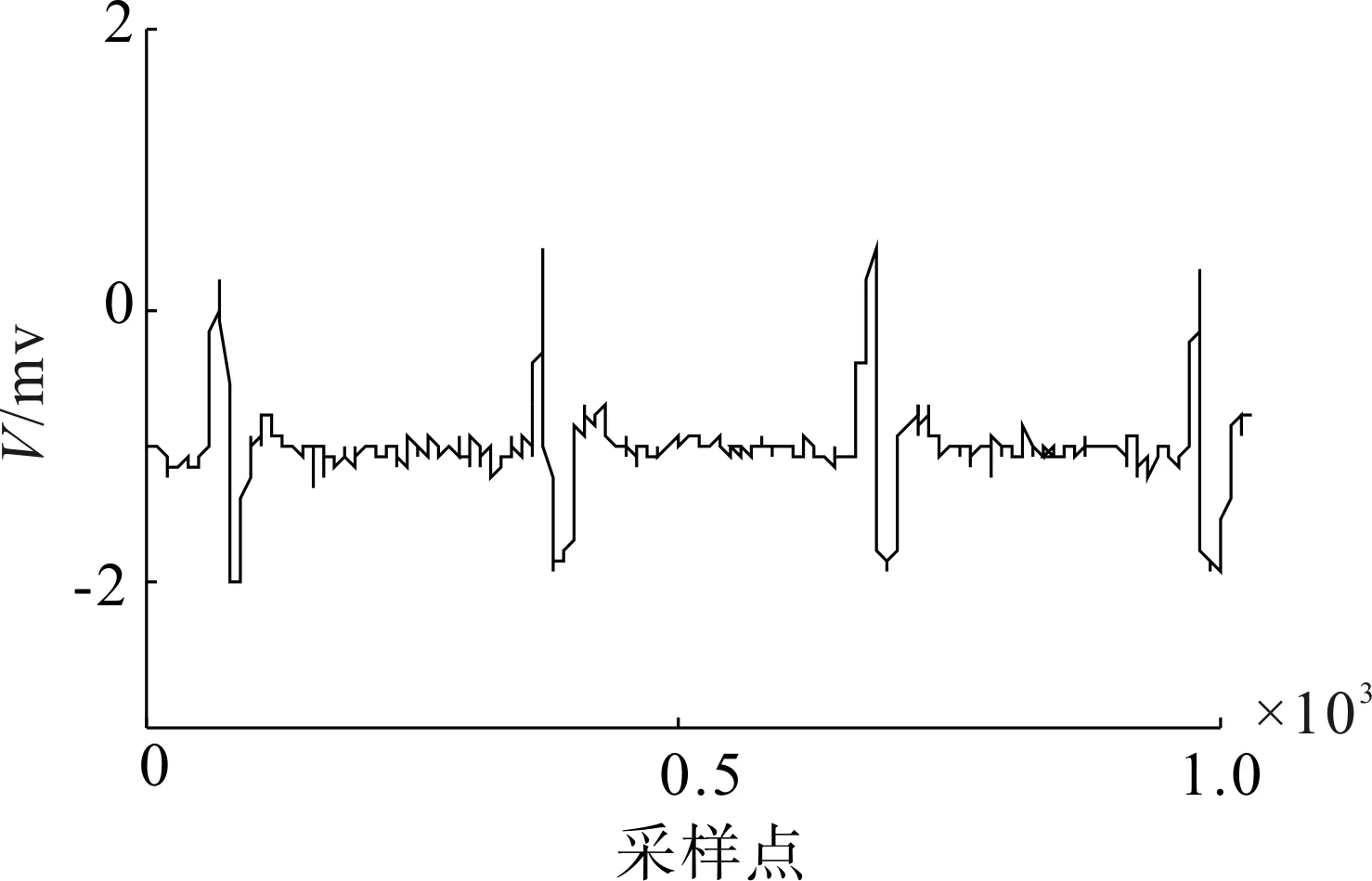
(a)小波熵算法去噪波形圖

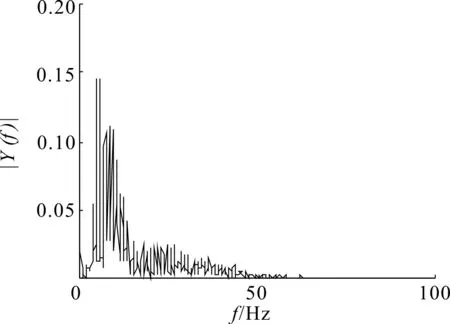
(b)小波熵算法去噪頻譜圖圖8 小波熵算法去噪波形及頻譜圖Fig.8 The waveform and spectrum of de-nosing signals of wavelet entropy algorithm

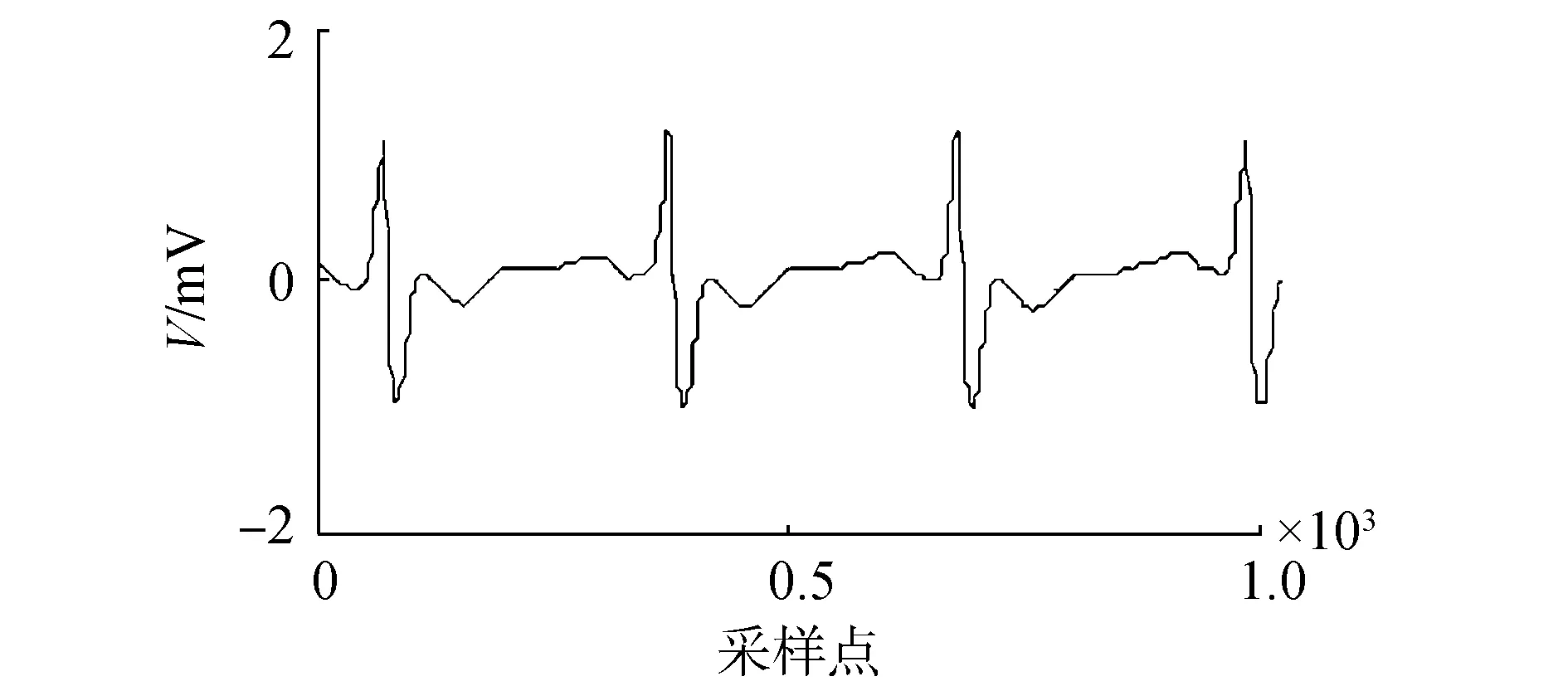
(a)本文算法去噪波形圖

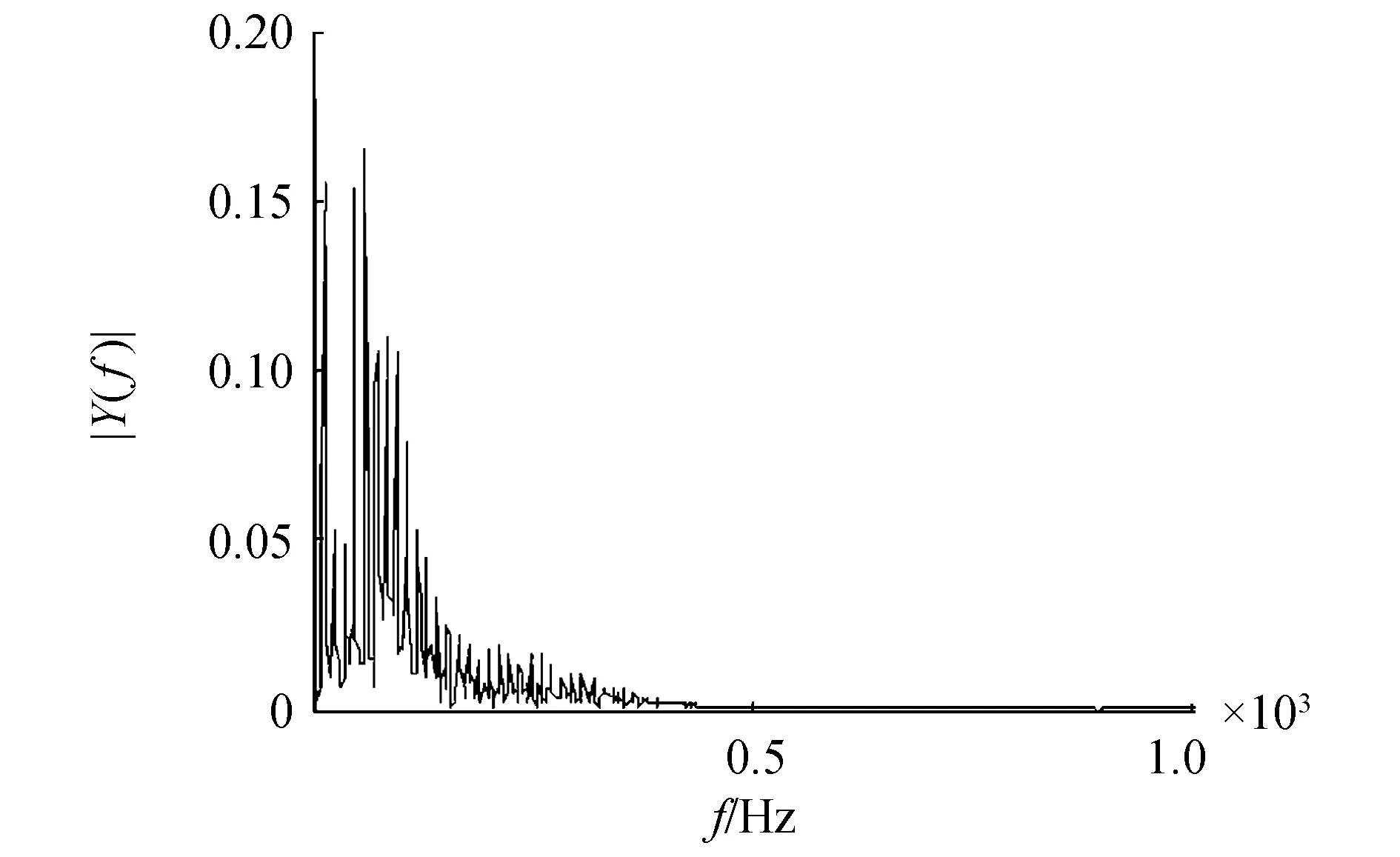
(b)本文算法去噪頻譜圖圖9 本文算法去噪波形及頻譜圖Fig.9 The waveform and spectrum of de-nosing signals of proposed algorithm

由圖6～9可以看出，該數據中工頻干擾不明顯，本文提出的算法去噪的波形含噪聲較少，波形無震蕩現象。說明對基線漂移和肌電噪聲去除效果要優于其他兩種算法。

3.4 定量分析去噪性能

為定量評價去噪效果，分別運用改進的小波閾值算法、小波熵去噪算法和本文提出的基于相關性的小波熵閾值去噪算法對含噪信號進行去噪。由于MIT-BIH數據庫中的數據原本就受多種噪聲干擾，不能得到理想“純凈”的信號，不便于計算SNR。因此采用MATLAB的心電模擬函數(ecg)模擬一段干凈的心電信號，通過疊加噪聲bw、em和ma，構造含噪信號。各算法去噪性能通過SNR、MSE和運行時間T來評價。去噪后的信號信噪比越高，則說明去噪效果越好；去噪后信號均方誤差越小，說明去噪后信號與原始信號重合度越高；運行時間越小，算法復雜度越小。分別如表1、表2和圖10所示。

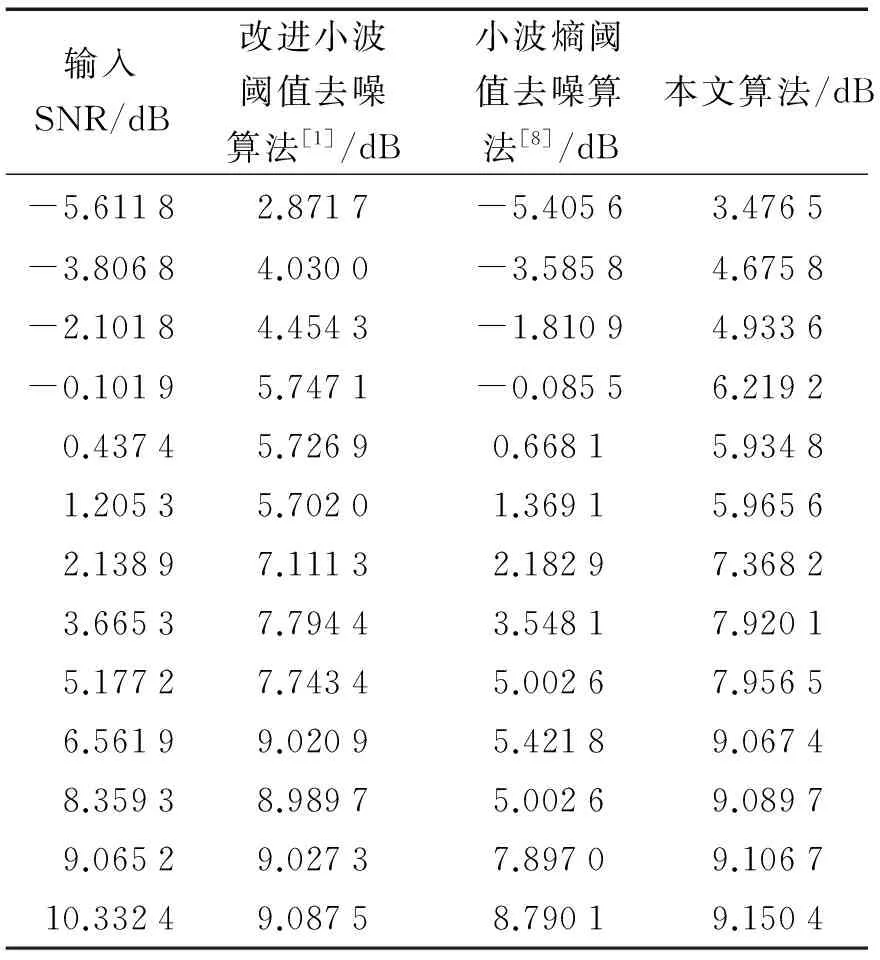
表1 不同信噪比下各算法去噪的信噪比

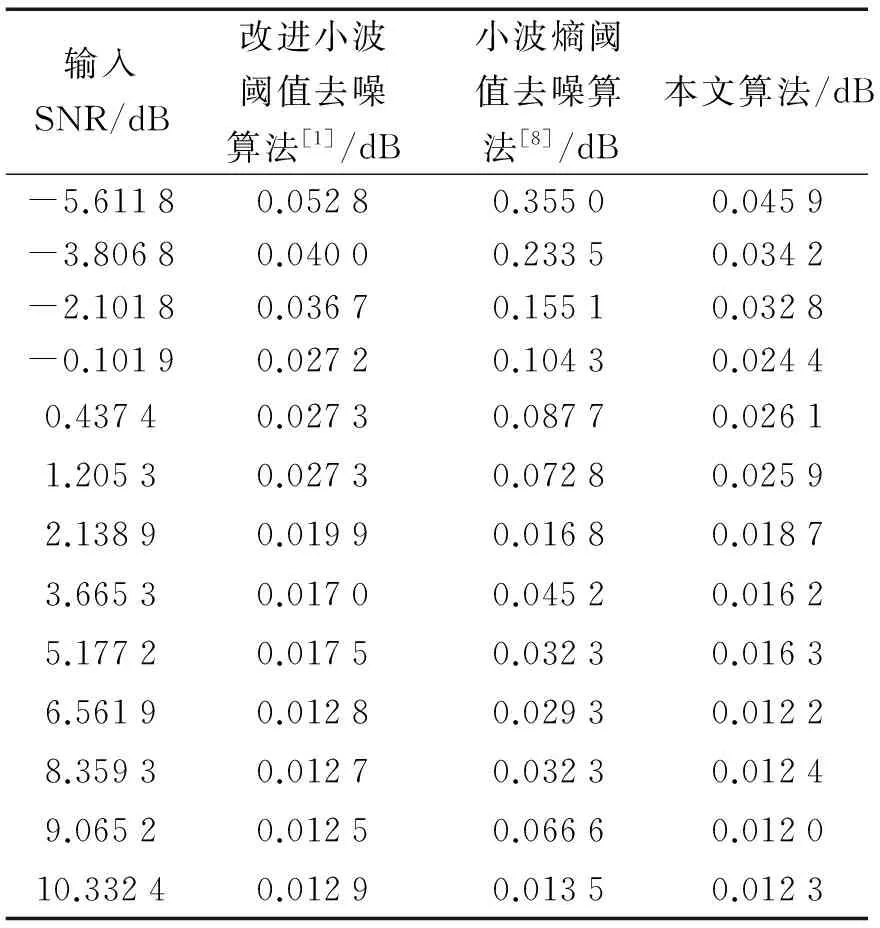
表2 不同信噪比下各算法去噪的均方誤差

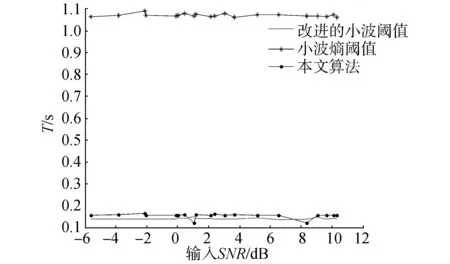
圖10 不同信噪比下3種算法去噪過程的運行時間Fig.10 The run time of three algorithms in different SNR

從表1和表2可以看出，當輸入信號的信噪比范圍從-5 dB～10 dB時,經過本文提出的算法去噪后在SNR和MSE上的結果都要優于改進的小波去噪法以及小波熵閾值去噪法，尤其在輸入信號信噪比較低時，優勢更明顯。輸入的3種噪聲比例不同，去噪結果稍有不同，小波熵閾值法基線漂移去除效果較差，在基線漂移占比大時，信噪比較低。

從圖10可以看出，本文算法的運行時間與改進的小波閾值算法相當，遠遠小于小波熵閾值算法。原因在于，小波分解、重構的過程復雜，算法復雜度較高相較計算閾值、相關性處理，運行時間較長。本文算法和改進的小波閾值去噪算法都只需要一次小波分解、重構；而小波熵閾值去噪需要兩重小波分解、重構，所以算法復雜度高。綜上可以看出，本文提出的去噪算法的去噪效果要優于其他兩種算法。

4 結束語

本文針對心電信號3種主要噪聲的特性，提出了一種基于相關性的小波熵心電信號去噪算法。算法可以在一次小波分解、重構的過程中，同時去除掉基線漂移、工頻干擾、肌電噪聲3種噪聲；利用各尺度間高頻小波系數的相關處理多次剔除有用信號，利用噪聲計算小波熵閾值具有自適應性；并選擇合適的閾值函數，避免波形震蕩。與其他去噪算法對比，復雜度較小，但去噪效果明顯提高。另外，實驗中發現在輸入噪聲信噪比特別小的情況下，去噪算法會對原始信號產生一定的損失，在以后的工作中將深入研究此問題。

[1]趙艷娜, 魏瓏, 徐舫舟, 等. 基于小波變換的心電信號去噪綜合算法[J]. 現代生物醫學進展, 2009, 9(16): 3128-3130. ZHAO Yanna, WEI Long, XU Fangzhou, et al. ECG signal denoising algorithm based on wavelet transform[J]. Progress in modern biomedicine, 2009, 9(16): 3128-3130.

[2]HARITHA C, GANESAN M, SUMESH E P. A survey on modern trends in ECG noise removal techniques[C]//Proceedings of 2016 International Conference on Circuit, Power and Computing Technologies (ICCPCT). Nagercoil: IEEE, 2016: 1-7.

[3]趙志華, 許愛華. 基于形態學的ECG小波自適應去噪算法[J]. 計算機工程與設計, 2008, 29(8): 2140-2142. ZHAO Zhihua, XU Aihua. ECG adaptive wavelet transform of denoising algorithm based on morphology[J]. Computer engineering and design, 2008, 29(8): 2140-2142.

[4]TAI Shenchuan, SUN C C, YAN W C. A 2-D ECG compression method based on wavelet transform and modified SPIHT[J]. IEEE transactions on biomedical engineering, 2005, 52(6): 999-1008.

[5]楊思軍, 郝繼飛, 閆文杰, 等. 小波濾波與QRS波檢測[J]. 計算機工程與應用, 2011, 47(12): 239-241. YANG Sijun, HAO Jifei, YAN Wenjie, et al. Wave filtering and QRS detection[J]. Computer engineering and applications, 2011, 47(12): 239-241.

[6]DONOHO D L. denoising by soft-thresholding[J]. IEEE transactions on information theory, 1995, 41(3): 613-627.

[7]AGANTE P M, DE SA J P M. ECG noise filtering using wavelets with soft-thresholding methods[C]//Proceedings of 1999 Computers in Cardiology. Hannover: IEEE, 1999, 26: 523-538.

[8]侯宏花, 桂志國. 基于小波熵的心電信號去噪處理[J]. 中國生物醫學工程學報, 2010, 29(1): 22-28, 34. HOU Honghua, GUI Zhiguo. Denosing processing of ECG signal based on wavelet entropy[J]. Chinese journal of biomedical engineering, 2010, 29(1): 22-28, 34.

[9]歐陽波, 程棟, 王玲. 改進小波閾值算法在心電信號去噪中的應用[J]. 計算機工程與應用, 2015, 51(4): 213-217. OUYANG Bo, CHENG Dong, WANG Ling. Improved wavelet threshold algorithm in application of ECG signal de-noising[J]. Computer engineering and applications, 2015, 51(4): 213-217.

[10]LI Nianqiang, LI Ping. An improved algorithm based on EMD-wavelet for ECG signal de-nosing[C]//Proceedings of 2009 International Joint Conference on Computational Sciences and Optimization. Sanya, China: IEEE, 2009, 1: 825-827.

[11]MALLAT S. 信號處理的小波導引[M]. 北京: 機械工業出版社, 2003.

[12]劉霞, 黃陽, 黃敬, 等. 基于經驗模態分解(EMD)的小波熵閾值地震信號去噪[J]. 吉林大學學報: 地球科學, 2016, 46(1): 262-269. LIU Xia, HUANG Yang, HUANG Jing, et al. Wavelet entropy threshold seismic signal denoising based on empirical mode decomposition (EMD)[J]. Journal of Jilin university: earth science edition, 2016, 46(1): 262-269.

[13]李文, 劉霞, 段玉波, 等. 基于小波熵與相關性相結合的小波模極大值地震信號去噪[J]. 地震學報, 2012, 34(6): 841-850. LI Wen, LIU Xia, DUAN Yubo, et al. Wavelet modulus maxima denoising of seismic signals based on combined wavelet entropy and correlation[J]. Acta seismologica sinica, 2012, 34(6): 841-850.

[14]ROSSO O A, BLANCO S, YORDANOVA J, et al. Wavelet entropy: a new tool for analysis of short duration brain electrical signals[J]. Journal of neuroscience methods, 2001, 105(1): 65-75.

[15]朱澤煌, 胡廣書, 郭恒, 等. MIT—BIH心電數據庫的開發及用作檢測標準[J]. 中國生物醫學工程學報, 1993, 12(4): 244-249, 243.

[16]徐效文, 曾超, 崔松野, 等. MIT-BIH數據庫心電數據重采樣研究[J]. 計算機工程與應用, 2011, 47(8): 245-248. XU Xiaowen, ZENG Chao, CUI Songye, et al. Research on resampling of ECG data from MIT-BIH database[J]. Computer engineering and applications, 2011, 47(8): 245-248.

王曉燕，女，1992年，碩士研究生，主要研究方向為信號處理、機器學習。

魯華祥，男，1965年，研究員，博士生導師，中國人工智能學會“神經網絡與計算智能”專業委員會主任、中科院半導體所高速電路與神經網絡實驗室主任，主要研究方向為類腦神經計算方法、微電子類神經計算芯片和系統研究、不確定性及非完全信息處理。獲北京市科學技術進步一等獎、“中國科學院盈科優秀青年學者獎”、國家發明三等獎、“國家‘八五’科技攻關重大科技成果獎”、“95電子十大科技成果獎”、全軍科技進步二等獎等獎勵。發表學術論文30余篇，合作出版專著1本，獲授權發明專利10項。

金敏，女，1985年，助理研究員，主要研究方向為信號處理、智能計算。

Wavelet entropy denoising algorithm of electrocardiogram signals based on correlation

WANG Xiaoyan1, LU Huaxiang1,2, JIN Min1, GONG Guoliang1, MAO Wenyu1, CHEN Gang1

(1. Institute of Semiconductors, Chinese Academy of Sciences, Beijing 100083, China; 2. Center for Excellence in Brain Science and Intelligence Technology, Chinese Academy of Sciences, Shanghai 200031, China)

In view of the baseline drift, power line interference and muscle noise of electrocardiogram (ECG) signals, the wavelet entropy denoising algorithm of ECG signals based on correlation was proposed. First, ECG signals were decomposed using wavelets to determine the number of scale of wavelet decomposition, and the lowest approximation coefficients were each set to zero, so as to remove the baseline drift. Then, the high-frequency wavelet coefficient of adjacent scales was processed by adaptively calculating the global threshold with the correlation coefficients between the adjacent scales, to remove the power line interference and the muscle noise. Last, the denoising signals were reconstructed using zero approximation coefficients and processed wavelet coefficients. Using this method, three kinds of noise were removed in one process of wavelet decomposition and reconstruction. Experiments using the MIT-BIH database and simulative data prove that the algorithm is much better than others in ECG denoising with low complexity.

electrocardiogram signals; denoising; correlation; wavelet entropy; adaptively

10.11992/tis.201611017

http://www.cnki.net/kcms/detail/23.1538.TP.20170111.1705.026.html

2016-11-15.

中國科學院戰略性先導專項(xdb02080002)；青年自然科學基金項目(61401423)；中國科學院國防實驗室基金項目(CXJJ-16S076).

魯華祥. E-mail: luhx@semi.ac.cn.

TP391

A

1673-4785(2016)06-0827-08

王曉燕，魯華祥，金敏，等. 基于相關性的小波熵心電信號去噪算法[J]. 智能系統學報， 2016, 11(6): 827-834.

英文引用格式：WANG Xiaoyan, LU Huaxiang, JIN Min， et al. Wavelet entropy denoising algorithm of electrocardiogram signals based on correlation[J]. CAAI Transactions on Intelligent Systems, 2016, 11(6): 827-834.