非連續變形分析方法及其在災害防治研究中的應用

趙興權, 張迎賓, 陳光齊,余鵬程, 黃小福, 陳巖巖

(1. 西南交通大學土木工程學院, 四川 成都 610031; 2. 九州大學土木建筑工程學院, 日本 福岡 819-0395)

非連續變形分析方法及其在災害防治研究中的應用

趙興權1, 張迎賓1, 陳光齊2,余鵬程1, 黃小福1, 陳巖巖1

(1. 西南交通大學土木工程學院, 四川 成都 610031; 2. 九州大學土木建筑工程學院, 日本 福岡 819-0395)

為了探究地震誘發地質災害的特征,用非連續變形分析方法(DDA, discontinuous deformation analysis)模擬了地震誘發崩塌、滑坡和防浪堤破壞的過程,著重探討了地震對災害發生過程及其運動能力的影響.在DDA程序中,整合了災害沖擊力的計算,結果表明:DDA方法可以計算滑體在地震作用下的運動情況;豎向地震動能夠顯著增強近斷層極震區滑坡的運動能力,可以很好地模擬地震誘發災害的全過程, 真實反應出危巖崩塌體、滑坡、防浪堤壩的破壞特征,能夠計算運動物體對既有建筑物的沖擊力,沖擊力的最大值遠遠超過了靜態側壓力值;文中算例結果顯示最大沖擊力是靜態側壓力的4倍多，該成果可為災害防護建筑物的選址、設計等從可靠和經濟的角度提供技術指導.

DDA;地震;地質災害;災害防治

由于復雜的地質作用,地殼(尤其是地表建筑基礎層)巖土體產生了尺度、方向、性質均不相同的裂隙,使建筑巖土基礎變成了復雜的塊體系統.塊體系統中復雜的裂隙結構控制著巖土體的力學性質和整個基礎的工程行為,復雜的裂隙以及被切割而成的巖土塊體特征往往直接影響著巖土體的整體強度,進而影響著整個巖土體結構的變形、穩定性和破壞后的運動特征.同時,當地震荷載作用在巖土體結構上時,也會使原本連續的整體結構產生一些裂縫,形成塊體系統.這些直接影響系統穩定性的非連續裂縫成為了工程設計中務必考慮的因素.然而,裂縫的存在產生了非連續的速度和位移場,這給工程實踐中廣泛使用的解析方法和普遍使用的連續數值模擬方法帶來了非常大的困難.針對這個問題,非連續的數值模擬方法應運而生.其中,富有代表性的非連續變形分析(discontinuous deformation analysis, DDA)方法是石根華[1]提出的解決此類離散結構系統(如巖體結構等)動態問題的有效方法,該方法最初的版本是二維DDA,之后三維DDA問世.自從DDA方法和數值代碼問世以來,該方法受到了研究者和工程師們的廣泛關注.學者們對初始DDA方法中的一些局限性進行了修正和擴展[2-9],使其在落石[10-13]、滑坡[14-22]、隧道[23-25]、爆破[26-28]、動力塊體[29-33]和其他工程應用[34-38]實踐中更加有效、實用.

DDA方法也應用于很多大型工程實踐中,如,中國的三峽工程[39-40]、美國科羅拉多Pueblo大壩[41]、美國圣弗朗西斯科Yerba Buena隧道[42]、挪威Gjovik奧林匹克洞[43]、以色列Masada國家紀念碑[44-45]等.

西南交通大學地震巖土工程研究組致力于地震誘發地質災害的全過程分析,以地震誘發滑坡為例,有兩個核心問題需要解決:一是地震荷載下,邊坡是否失穩以及動力響應[46],即地震邊坡穩定性分析問題;二是邊坡失穩形成滑坡后,如何運動的問題,即地震誘發滑坡的運動性分析問題.地震荷載作用下,巖土體結構尤其是由不連續界面控制其穩定性的巖石類結構,一般較為容易受到破壞,其破壞后的運動特性往往表現出很大的離散性.解決此類問題,DDA較之其他方法,具有明顯的優勢.本課題組將DDA方法應用于地震誘發地質災害的上述兩個核心問題的研究中.本文首先簡要介紹DDA方法的基本原理,然后利用DDA方法進行地震邊坡穩定性、地震滑坡(包括危巖崩塌體)的運動特性、地震滑坡對既有建筑物的沖擊作用及海嘯作用下防浪堤的破壞等的分析,最后,對應用DDA方法進行地震誘發滑坡從變形、失穩、破壞、運動、堆積全過程進行數值模擬的可能性進行展望和討論.

1 DDA方法概述

1.1 DDA基本原理

DDA方法基于塊體理論建立平衡方程,塊體的幾何形狀沒有特殊的限制,可是任意形狀,其中每一個塊體可以獨立移動和變形,塊體之間的相互作用通過接觸彈簧來實現,塊體之間能夠實現分離和接觸,相互作用時嚴格遵守“不嵌入、不張拉”原則.

對于一個二維問題,任意形狀的每一個塊體擁有6個自由度,其中, 3個是剛體位移變量, 3個為應變常量,因此,第i塊的變形為

Di=[u0v0r0εxεyγxy]T,

(1)

式中:

(u0,v0)為塊體內指定點(x0,y0)的剛體位移;

r0為以(x0,y0)為轉動中心的塊體的轉角;

εx、εy、γxy為塊體的x、y方向正應變和剪應變.

塊體中任意一點(x,y)的位移(u,v)為

(2)

(3)

式中:

Ti為位移變換矩陣.

DDA方法中,各個塊體是相互連接的,n個單獨的塊體單元連通過邊界條件和接觸條件后的總體方程為

(4)

式中:Kij為6×6的總體剛度矩陣(因為每個塊體有6個自由度);Di為6×1的總體位移矩陣,其具體表達式如式(1)所示; [Fi]為6×1的總體荷載矩陣.

DDA是一種完全動力的分析方法,求解方程(4)后,得出每一個塊體的實時位移和變形,根據塊體間“不嵌入、不張拉”原則,重新調整形成新的總體剛度矩陣,進行下一步的計算.通過不斷的修正迭代計算,直至計算完成.

2 DDA在地震誘發地質災害中的應用

我國是一個地震頻發的國家,每年由地震造成的人員傷亡及經濟損失都非常嚴重，尤其在西南山區,往往造成巨大損失的是由地震引發的地質災害.據殷躍平等[47]的統計,僅汶川地震中造成的地質災害達15 000多處,多以崩塌、滑坡、泥石流為主,而且,地震也往往導致交通橋梁、隧道等因位移、變形過大而遭到破壞,堵塞交通.因此,對于地震造成的各類地質災害問題亟待研究, DDA方法尤其適合解決此類問題(如圖1).

圖1 地質災害的DDA分析結果Fig.1 DDA results of geological disaster

2.1 近斷層地震對大型滑坡的影響[22]

汶川地震[48]造成了許多大型滑坡,其中,大光包滑坡是此類滑坡的典型代表.就大光包滑坡而言,滑動距離4.5 km,堆積體寬度2.2 km,滑坡-碎屑流面積約10 km2,估算體積約7.5億km3,由滑坡堆積體形成的堰塞壩高達690 m,大光包滑坡規模巨大,是近斷層地震滑坡的典型,此類滑坡滑移距離遠,滑動能力強,造成危害巨大,因此,從汶川地震后,對此類滑坡的研究也越來越多.結合此類滑坡的特征,利用DDA方法分析其運動特性及堆積特征等,對于居民區修建避開此類滑坡具有指導意義.

大光包滑坡從地質結構來看,是典型的順層滑坡[22].距離斷層位置近(約6.5 km)和規模巨大(約8×105km3)是其突出特征.近斷層極震區的位置意味著大光包斜坡受到強烈的豎向地震動作用,巨大的規模則要求考慮尺寸效應.因此,在用DDA方法對大光包滑坡模擬時,必須考慮以上因素.對于近斷層因素,通過改進的地震波輸入方法輸入多向地震荷載來解決這個問題;對于效應因素,依據虎克-布朗破壞準則來反分析材料強度以考慮滑坡的尺寸效應.

根據黃潤秋等[49-51]的地質調查結果,大光包滑坡前后的二維地質模型如圖2所示, DDA方法對大光包滑坡的模擬可以采用簡化的模型如圖3所示.DDA方法中的地震荷載輸入方式[52]包括加速度時程輸入、速度時程輸入和位移時程輸入.選擇加速度時程輸入作為本次地震荷載輸入方式,具體是將加速度荷載當作體積力施加到基巖上.

圖2 汶川地震后大光包滑坡發生前后地形橫截面圖Fig.2 Cross-sections of the Daguangbao landslide before and after Wenchuan earthquake

圖3 大光包滑坡的DDA模型Fig.3 DDA model of the Daguangbao landslide

計算中各材料物理參數、模型控制參數如表1、2所示.基巖材料經分析,其密度及重度取如表1中虛擬值較為符合實際[22],如沒有特別說明,本文中基巖密度及重度均為虛擬值.

DDA模擬大光包滑坡的全過程如圖4所示.對于一個潛在滑坡的動力行為的估計對減少滑坡災害具有非常重要的意義,尤其滑坡的運動距離是風險評估和防護措施設計的重要參數.超遠距離滑移是大多數地震誘發的大型滑坡的特點,許多學者都致力于研究滑坡遠距離滑移的機理.但是,考慮到地震滑坡是一個動力問題,潛在滑坡在初始階段及破壞運動階段都受到復雜的多向地震荷載作用,因此,對于地震誘發的超遠距離滑坡的數值模擬顯得尤為迫切.

表1 物理參數Tab.1 Physical parameters of materials

表2 控制參數Tab.2 Control parameters

為了驗證地震作用對滑坡運動距離的影響,同時分析了靜態、僅水平地震動、水平地震動和豎向地震動耦合3種情形時的結果.靜態情形即自然狀態時,大光包斜坡保持穩定,僅在上部產生一定的變形,僅有水平地震荷載時,滑坡前緣移動距離為944 m,當水平地震荷載和豎向地震荷載同時施加到模型上時,滑坡前緣移動距離為1 901 m,此時,堆積形態與實際狀況吻合.由此可以得出,對于近斷層滑坡,豎向地震動有顯著的影響.同時,通過對粘聚力及內摩擦角對于滑坡運動的敏感性分析結果顯示,粘聚力的取值對滑坡運動特性的影響較小,而內摩擦角的取值明顯影響著滑坡的運動特性.

由以上分析結果可以看出,對大光包滑坡的DDA模擬能夠很好的再現大光包滑坡啟動、滑移及最后堆積的全過程,同時也證實了處于近斷層極震區的滑坡,其滑移距離遠,造成的危害也大,這對于類似問題的分析有著很好的借鑒,通過DDA方法,也可以對一些類似的潛在滑坡進行危險性評估和設計一些防護措施.

圖4 DDA模擬大光包滑坡全過程Fig.4 Whole processes of DDA simulation of the daguangbao landslide

2.2 地震誘發危巖崩塌的運動特性研究

危巖是指位于陡峭山坡邊緣被巖體結構面切割的巖石塊體,經由重力、地震、風、裂隙水壓力等荷載作用下,容易沿著山體滾落.危巖脫離母巖向下滾落的過程中,其運動形式復雜,軌跡因在下落過程中多次與山體碰撞而難以確定.雖然其規模不大,但由于具有高速運動的特性,對其影響范圍內的建筑物造成很大的損害.地震荷載是造成危巖崩塌的最常見因素之一,地震不僅直接引起危巖體崩塌,其強烈的荷載作用常常能引起裂隙擴張,增加危巖崩塌隱患.因此,研究地震荷載對于危巖崩塌破壞的影響,是目前關于此類災害問題的研究熱點[53].本團隊對此進行了一些初步研究，部分成果已錄用待刊,部分研究成果如下.

建立如圖5所示的概念危巖,研究不同的荷載組合及不同的地震波輸入方式對于危巖崩塌體運動特性的影響,確定地震荷載對于危巖運動特性的促進程度,這將會對地震危巖崩塌災害的防治提供指導意見.

DDA計算中,地震荷載的作用是通過將加速度以體積力的方式施加到基巖上來實現的.計算中參數取值如表3～5所示.

圖5 概念危巖Fig.5 The assumed perilous rock

項目數值單步允許最大位移率0.001時間步/s0.001彈簧剛度/Pa4×1011超松弛系數1.3時步數7×104

建立如下4種工況來分析危巖在地震工況和非地震工況下的動力效應:

GK1(工況1):天然工況(無地震波);

GK2(工況2):水平地震波;

GK3(工況3):豎向地震波;

GK4(工況4):水平地震波、豎向地震波耦合作用.

表4 模型物理參數Tab.4 Model material parameters

表5 模型節理參數Tab.5 Model joint parameters

研究結果表明,在天然工況下,危巖只受重力作用,只是存在一定的變形,危巖整體能夠保持穩定.3種地震工況下,危巖崩塌破壞過程如圖6所示.

盡管3種地震波輸入方式不同,危巖的破壞方式均是傾倒破壞.根據運動特點,危巖在3種不同的工況下,從穩定狀態到最終破壞的變化過程可分為3個階段:裂隙擴張貫通及危巖傾倒階段、拋射階段、停積階段.為了解3種地震波輸入方式對危巖破壞后運動特性的影響,各工況下塊體的位移如表6所示.

圖6 不同地震工況下危巖崩塌破壞過程Fig.6 Perilous rock failure processes under different seismic excitations

項目GK2GK3GK4(GK4-GK2GK2)/%(GK4-GK3GK3)/%(GK3-GK2GK2)/%脫離母巖時間/s26.1033.2622.60-13.4-32.12.7崩塌塊體最大水平位移/m684.53699.70826.0820.618.12.2崩塌塊體平均水平位移/m189.93204.64205.908.40.67.7崩塌塊體最大位移比2.892.963.5121.518.62.4崩塌塊體最小位移比0.680.690.714.42.92.9崩塌塊體平均位移比1.011.071.086.90.95.9

注: 位移比為某塊體的最終水平位移/最終豎向位移;最大位移比為所有崩塌塊體最終水平位移與最終豎向位移之比的最大值;最小位移比為所有崩塌塊體最終水平位移與最終豎向位移之比的最小值;平均位移比為所有崩塌塊體最終水平位移與最終豎向位移之比平均值.

3種地震工況下崩塌塊體位移比分別為1.01、1.07、1.10,明顯大于非地震條件下的0.50[54],由此可以得出,地震荷載不僅直接誘發危巖崩塌破壞的發生,而且對危巖崩塌體的運動距離有促進作用.

觀察圖6不同地震工況下危巖崩塌體運動的全過程,發現在3種不同地震工況下,工況4無論是脫離母巖破壞時間,停積時間,還是塊體的最大水平位移、平均水平位移較之工況2、3均更加顯著.工況4下塊體的最大水平位移較之工況2、3分別增大20.6%和18.1%,平均水平位移較工況2、3分別增大8.4%和0.6%.

另外,無論是塊體最大位移比、最小位移比還是平均位移比,工況4的數值都是最大的,由此可見危巖在工況4最容易發生破壞,破壞后崩塌塊體的影響范圍最大,可能的危害程度最高,是最值得注意的情況.

對比工況2、3可以明顯的發現,工況3較之工況2,塊體的最大水平位移和平均水平位移分別增大了2.2%和 7.7%,其他包括最大位移比、最小位移比、平均位移比都增加了,可見在某些情況下豎向地震荷載對崩塌塊體的影響程度大于水平向地震荷載對其的影響程度.其他學者對于此問題也有相同的發現[55],這種情況在汶川地震中尤為突出.因此,在抗震的防治措施中,應當給予豎向地震動足夠的重視,只有這樣才能有效達到抗震設防和災害防治的目的.

由此例的分析過程可知,DDA方法適合研究危巖崩塌體的運動特性.通過研究發現,地震不僅引起危巖崩塌的發生,而且對于其運動距離具有顯著影響,并且在此例中,豎向地震動的影響要比水平地震動的影響更為顯著,這應該引起工程設計人員的注意.

2.3 對地震誘發滑坡的運動過程的模擬

地震發生時常常伴隨著大量滑坡等地質災害的產生,這些地質災害對民居、交通等造成了很大的破壞[56-57].自有記錄以來,許多由地震誘發的滑坡給人民的生命和財產帶來了巨大的損失.2008年,汶川大地震總共誘發了60 100余處滑坡,這些滑坡直接造成了超過20 000多人死亡[58],同時其造成的財產損失占到總損失的三分之一以上.弄清地震誘發滑坡的運動特性,測算滑坡的運動距離和范圍,對于地震滑坡災害的防治工作有重大意義.

現有的研究中,對于地震誘發的大型滑坡的遠程運動現象,大多采用強度折減模型來完成,很少有考慮到滑坡運動過程中地震荷載與滑坡的相互作用.通過研究地震荷載與滑坡的相互作用,提出MAM(復合加速度模型)[52,59]進行數值模擬.以發生在汶川地震中的東河口大型滑坡為例,根據其離散性和大位移等特點,利用DDA再現了東河口滑坡的運動過程,合理的解釋了其遠程運動特性[52]. DDA模擬東河口滑坡的計算中模型參數取值如下表7、8所示.

為了對比是否需要考慮地震荷載與滑坡在運動過程中相互作用,建立了兩個模型.未考慮相互作用的靜態DDA模型和考慮相互作用的復合加速度動態DDA模型.圖7分別記錄了不同時刻兩個模型中滑坡的運動形態.

表7 模型物理參數Tab.7 Model material parameters

表8 模型控制參數Tab.8 Model control parameters

對比模型的計算結果和災后東河口地形圖可以發現:考慮了地震荷載與滑坡相互作用的模型的計算結果中,其巖土體材料堆積形態與災后地形基本一致;未考慮相互作用的模型計算結果與實際情況相差較大.此模擬結果也證明了考慮了蹦床效應的復合加速度模型在模擬地震荷載與滑坡相互作用領域的適用性.同時,也用實例論證了DDA模擬地震誘發滑坡的運動過程的可行性.

2.4 地質災害對既有建筑物的沖擊力

DDA方法在處理非連續大位移問題上表現出極大的優勢,將塊體位移不變量作為基本未知量,利用接觸彈簧假定處理塊體之間的相互作用,并應用最小勢能原理列出系統平衡方程,方程的解即為系統的位移增量.這種方法有著嚴密的數學基礎及完備的能量守恒,可以完整地分析塊體運動情況,特別適合巖體滑坡的計算.由于DDA方法的基本未知量形式及方程的建立方式,在以往的DDA研究及應用中,主要偏向于系統運動特征的描述,如落石的運動距離,滑坡的持續時間和滑體的堆積形狀等.而對于系統的力學特征,如落石對基巖的作用、滑體對下游結構的沖擊力并不常涉及.在實際問題中,研究對象的力學參數,往往與其運動特征同等重要[60].例如,在研究滑體對下游結構的作用時,如果能得出滑體對結構的沖擊力大小隨時間的變化曲線,則可以得出結構受到的外界作用力,這對防治由地質災害對民居以及公共設施的破壞[61]等具有很好的指導.

(a)未考慮MAM相互作用(靜態)(b)考慮MAM相互作用(動態)圖7 東河口滑坡DDA模擬結果Fig.7 DDAsimulationresultsoftheDonghekoulandslide

DDA方法已經可以模擬塊體系統任意時刻的運動情況.在系統運動已知的情況下,系統中存在的作用力也可以唯一確定.但是,整個系統的受力情況是復雜耦合的,要得到某些塊體間的相互作用力,最主要的任務是在系統中存在的所有力中識別出這些塊體間作用力,并以適當的方式處理和累加.DDA方法在求解整體平衡方程后,通過已解出的基本未知量可以反推塊體受力情況,但此時只能得到作用在塊體形心上的合力.事實上,即使是兩個塊體之間的作用力,也可能處于不同的位置.如果需要研究位于某條邊上的作用力,則需要對兩塊體間的作用力進一步識別.

通過分析DDA方法基本理論,不難發現,在不考慮錨桿連接的情況下,塊體之間的相互作用力全部來源于塊體間的由接觸彈簧帶來的接觸彈簧力和摩擦力.對于碰撞過程,摩擦力相對較小,可以忽略不計.因此,分析當前系統存在的所有接觸力,即可得到指定塊體間的作用力.通過在DDA程序中插入代碼,可以獲得接觸力的所有屬性.若需要得出其他塊體對某個目標塊體指定邊的作用力,則要求篩選出所有包含其他塊體和目標塊體指定邊的所有接觸,并按照方向累加.在摩擦力不可忽略的情況下,則還應將摩擦力納入.在此基礎上編寫程序,便可以得出目標塊體指定邊受到其他塊體的作用力.圖8、9是塊體作用力研究的應用模型，該滑坡基于東河口滑坡相關資料,研究對象是處于滑坡下游的結構物.

(a) 滑坡發生前

(b) 滑坡發生后圖8 沖擊力研究模型(單位： m)Fig.8 The model of impact research (unit: m)

拓展的DDA程序在處理大量塊體對結構沖擊作用時有著獨特的優勢,但仍有部分問題需要引起注意.程序中接觸彈簧剛度的數值會影響接觸力的大小和整個碰撞持續時間.對于已知材質的塊體,在固定碰撞速度下的碰撞時間是可以測得的，認為碰撞時滿足彈性碰撞,如果需要取得較為精確的碰撞力,可以通過碰撞時間反推接觸彈簧剛度,從而確定碰撞過程和任意時刻的沖擊力大小.另外,在特定條件下,塊體受到的沖擊力可能被重復計算導致結果比實際情況偏大.這一方面是因為DDA在處理邊-邊接觸時,將其分解為兩個角與邊接觸,另一方面是因為目標塊體和沖擊塊體共節點.為了避免這種情況,只需在模型建立時注意即可.

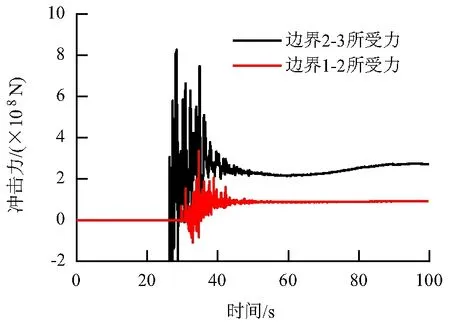
圖9 塊體對結構不同邊的作用力Fig.9 The impact of different edge of structure by blocks

2.5 利用DDA對防浪堤進行破壞過程模擬[62-63]

防浪堤是一種常見的海岸水工構筑物,主要起消浪減流的作用,可以保護沿海地區海岸、港口及其他建筑物免受海浪侵蝕和破壞.在實際工程中,防浪堤的穩定性是一項重要的設計內容.在科研領域,國內外許多學者對防浪堤的穩定性分析方法進行了大量的研究,并取得了一定的成果.然而,在2011年,因日本東北大地震(震級9.0級)產生的巨大海嘯,破壞了位于日本釜石市某海灣中一條沉箱型混合式防浪堤.目前,結合其實際破壞過程,已有的各種防浪堤破壞模型尚無法解釋該防浪堤的破壞機理.陳光齊、張迎賓[62-63]等提出了由管涌現象產生的局部破壞模型,利用DDA方法,并結合模型試驗再現了該防浪堤的破壞過程,提供了一種新的防浪堤的穩定性分析方法.

該防浪堤上部是方形混凝土結構,內部滲透系數小,可忽略滲流作用，下部由堆石斜坡堤作為基礎,稱毛石基礎,滲透系數較大.防浪堤的具體尺寸參數見圖10.DDA計算中模型各參數的取值見表9.與以往海嘯不同,此次海嘯產生的風浪周期很長,由幾分鐘到以小時計不等.結合該防浪堤的結構特點及工況建立了管涌局部破壞模型(圖10).

圖10 釜石市防浪堤模型(單位: m)Fig.10 Model of the breakwater in Kamaishi (unit: m)

項目滑體密度ρ/(kg·m-3)2000重度wy/(kN·m-3)20彈性模量E/GPa1.0泊松柏ν0.2內摩擦角φ/(°)35粘聚力c/MPa0彈簧剛度/Pa1.0×108時間步/s0.001

較長的風浪周期使得防浪堤兩側在較長時間內保持了相近的水力梯度值,視為一常量.在該時間段內,毛石基礎內部的滲流可看作是穩定滲流過程,滲透壓力被視為擬靜力作用在DDA塊體上.在該水力耦合模型中,滲透壓力通過以下3步導入: (1) 利用有限元計算出在穩定滲流情況下,該模型上任一點橫向與縱向水壓; (2) 導出有限元網格上每一節點上的水頭及相應的節點坐標; (3) 建立一個覆蓋毛石基礎且網格大小合適的網絡,結合第二步導出的水頭值,利用Kriging插值法,計算出該網格上每個網點上的水頭值,如圖11所示.

圖11 DDA模型上水頭網格分布Fig.11 DDA model simulate experiment model and water pressure field definition

為了驗證該破壞模型的合理性,以實際過程中出現的最大水頭差為例，再現了防浪堤由穩定到發生局部破壞,最后出現整體失穩的整個過程,如圖12所示.

從圖12(a)～(c)可知,在靠近港口一側,與沉箱型堤棱角接觸處的毛石基礎上出現了明顯的管涌現象,然后導致發生基礎局部失穩,最后出現防浪堤的整體失穩.在利用DDA方法分析的同時，為了更好地了解防浪堤的實際破壞過程，在前期工作中，根據實際建造的防浪堤情況建立了實驗模型，通過實驗成功地再現了防浪堤的破壞過程,如圖13所示[64].與DDA分析的結果相對比,發現DDA模擬過程可以真實地反應管涌破壞的過程,同時從側面也證實了DDA在解決非連續性較強的工程問題的優越性.

(a)

(b)

(c) 圖12 防浪堤的破壞模擬過程Fig.12 Failure process of the breakwater

圖13 滲流引起管涌破壞的實際過程Fig.13 The local failure due to piping induced by seepage flow

較長的風浪周期導致防浪堤于較長時間內在靠近外海一側和靠近港口一側形成了很大的水頭差.同時又因為毛石基礎的透水性較強及其材料結構較為松散的性質,使得毛石基礎由于較大的滲透壓力率先發生局部破壞,達到一定程度后,進而發生了包括混凝土沉箱結構在內的整體破壞.利用DDA模擬防浪堤的破壞過程,使得毛石基礎的離散性得到了充分地體現,完整的模擬出了毛石基礎由局部石塊發生較大位移而產生局部破壞.這是其他有限元方法無法準確做到的.

3 結 論

巖土工程問題,尤其是由不連續結構面即節理控制其變化的巖體結構材料,如若根據以往的連續性手段分析,往往因為不能很好的模擬出其離散的性質,分析過程受到了很多限制,也經常得不到符合實際的結論.非連續變形分析方法(DDA)的出現很好的解決了這個問題,隨著DDA方法本身的不斷改進及發展,越來越多的研究者將其運用于解決各類巖土問題中.本文主要通過講述幾個本團隊近年來利用DDA解決地震巖土工程問題的實例,來進一步的擴展DDA方法的工程應用,并根據上述分析,得出如下幾點結論:

(1) DDA方法可以很好地模擬地震導致災害的全過程,真實地反應出危巖崩塌體、滑坡、防浪堤壩的破壞特征;

(2) 處在近斷層極震區的滑坡,豎向地震動能夠顯著的增強滑坡的運動特性,這類滑坡的遠距離滑移往往受多個方向地震動耦合作用的影響.改進的DDA方法具有輸入不同地震荷載組合的優勢,能夠很好的分析這類問題;

(3) DDA方法具有分析由穩定階段到破壞階段全過程的能力,能夠反映出不連續結構面從局部破壞逐漸蔓延至全局破壞的過程,通過對此過程的細化分析,準確把握結構的破壞機理,以此為依據,可以提供可靠的改善方案;

(4) 改進的DDA方法能夠計算各類地質災害對于防護建筑物的沖擊力,利用求得的沖擊力的大小修建符合實際的防護支檔結構,指導工程設計人員設計各類防護措施具有重要的意義.

[1] SHI G H. Discontinuous deformation analysis a new numerical model for the ststic and dynamics of block systems[D]. Berkely: University of Califormia, Berkely, 1988.

[2] KE T C. The issues of rigid-body rotation in DDA. First international forum on discontinuous deformation analysis (DDA) and simulations of discontinuous media[M]. Berkeley: [s. n.], 1996: 18-25.

[3] LIN C T, AMADEI B, JUNG J, et al. Extensions of discontinuous deformation analysis for jointed rock masses[C]∥International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts. Pergamon: [s. n.], 1996: 671-694.

[4] CHEN G Q, MIKI S, OHNISHI Y. Development of the interactive visualization system for DDA[C]∥Proceedings of the 9th International Conference on Computer Methods and Advances in Geomechanics. Wuhan: [s. n.], 1997: 495-500.

[5] KOO C Y, CHERN J C. Modification of the DDA method for rigid block problems[J]. International Journal of Rock Mechanics and Mining Sciences, 1998, 35(6): 683-693.

[6] CHENG Y M. Advancements and improvement in discontinuous deformation analysis[J]. Computers and Geotechnics, 1998, 22(2): 153-163.

[7] DOOLIN D M, SITAR N. Time integration in discontinuous deformation analysis[J]. Journal of Engineering Mechanics, 2004, 130(3): 249-258.

[8] DOOLIN D M. Unified displacement boundary constraint formulation for discontinuous deformation analysis (DDA)[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2005, 29(12): 1199-1207.

[9] WANG L, JIANG H, YANG Z, et al. Development of discontinuous deformation analysis with displacement-dependent interface shear strength[J]. Computers and Geotechnics, 2013, 47: 91-101.

[10] CHEN Guangqi. Numerical modeling of rock fall using extended DDA[J]. Chinese Journal of Rock Mechanics and Engineering, 2003, 22(6): 926-931.

[11] WU J H, OHNISHI Y, NISHIYAMA S. A development of the discontinuous deformation analysis for rock fall analysis[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2005, 29(10): 971-988.

[12] MA G C, MATSUYAMA H, NISHIYAMA S, et al. Practical studies on rockfall simulation by DDA[J]. J. Rock Mechanics Geotech Engineering, 2011, 3(1): 57-63.

[13] CHEN G, ZHENG L, ZHANG Y, et al. Numerical simulation in rockfall analysis: a close comparison of 2-D and 3-D DDA[J]. Rock Mechanics and Rock Engineering, 2013, 46(3): 527-541.

[14] SITAR N, MACLAUGHLIN M M. Kinematics and discontinuous deformation analysis of landslide movement[C]∥2nd Panamerican Symp. on Landslides. Rio de Janeiro: [s. n.]. 1997.

[15] SITAR N, MACLAUGHLIN M M, DOOLIN D M. Influence of kinematics on landslide mobility and failure mode[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2005, 131(6): 716-728.

[16] WU J H. Applying discontinuous deformation analysis to assess the constrained area of the unstable Chiu-fen-erh-shan landslide slope[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2007, 31(5): 649-666.

[17] KVELDSVIK V, EINSTEIN H H, NILSEN B, et al. Numerical analysis of the 650 000 m2?knes rock slope based on measured displacements and geotechnical data[J]. Rock Mechanics and Rock Engineering, 2009, 42(5): 689-728.

[18] WU J H, LIN J S, CHEN C S. Dynamic discrete analysis of an earthquake-induced large-scale landslide[J]. International Journal of Rock Mechanics and Mining Sciences, 2009, 46(2): 397-407.

[19] WU J H. Seismic landslide simulations in discontinuous deformation analysis[J]. Computers and Geotechnics, 2010, 37(5): 594-601.

[20] WU J H, CHEN C H. Application of DDA to simulate characteristics of the Tsaoling landslide[J]. Computers and Geotechnics, 2011, 38(5): 741-750.

[21] ZHANG Y, CHEN G, ZHENG L, et al. Numerical analysis of the largest landslide induced by the Wenchuan earthquake, May 12, 2008 using DDA earthquake-induced landslides[M]. [S. l.]: Springer Berlin Heidelberg, 2013: 617-626.

[22] ZHANG Y, CHEN G, ZHENG L, et al. Effects of near-fault seismic loadings on run-out of large-scale landslide: a case study[J]. Engineering Geology, 2013, 166: 216-236.

[23] YEUNG M R, LEONG L L. Effects of joint attributes on tunnel stability[J]. International Journal of Rock Mechanics and Mining Sciences, 1997, 34(3/4): 348e1-348e18.

[24] WU J H, OHNISHI Y, NISHIYAMA S. Simulation of the mechanical behavior of inclined jointed rock masses during tunnel construction using discontinuous deformation analysis (DDA)[J]. International Journal of Rock Mechanics and Mining Sciences, 2004, 41(5): 731-743.

[25] TSESARSKY M, HATZOR Y H. Tunnel roof deflection in blocky rock masses as a function of joint spacing and friction A parametric study using discontinuous deformation analysis (DDA)[J]. Tunnelling and Underground Space Technology, 2006, 21(1): 29-45.

[26] NING Y, YANG J, AN X, et al. Simulation of blast induced crater in jointed rock mass by discontinuous deformation analysis method[J]. Frontiers of Architecture and Civil Engineering in China, 2010, 4(2): 223-232.

[27] NING Y, YANG J, AN X, et al. Modelling rock fracturing and blast-induced rock mass failure via advanced discretisation within the discontinuous deformation analysis framework[J]. Computers and Geotechnics, 2011, 38(1): 40-49.

[28] NING Y, YANG J, MA G, et al. Modelling rock blasting considering explosion gas penetration using discontinuous deformation analysis[J]. Rock Mechanics and Rock Engineering, 2011, 44(4): 483-490.

[29] HATZOR Y H, FEINTUCH A. The validity of dynamic block displacement prediction using DDA[J]. International Journal of Rock Mechanics and Mining Sciences, 2001, 38(4): 599-606.

[30] MACLAUGHLIN M, SITAR N, DOOLIN D, et al. Investigation of slope-stability kinematics using discontinuous deformation analysis[J]. International Journal of Rock Mechanics and Mining Sciences, 2001, 38(5): 753-762.

[31] DOOLIN D M, SITAR N. Displacement accuracy of discontinuous deformation analysis method applied to sliding block[J]. Journal of Engineering Mechanics, 2002, 128(11): 1158-1168.

[32] TSESARSKY M, HATZOR Y H, SITAR N. Dynamic displacement of a block on an inclined plane: analytical, experimental and DDA results[J]. Rock Mechanics and Rock Engineering, 2005, 38(2): 153-167.

[33] BAKUN-MAZOR D, HATZOR Y H, GLASER S D. Dynamic sliding of tetrahedral wedge: The role of interface friction[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2012, 36(3): 327-343.

[34] YEUNG M R. Analysis of a mine roof using the DDA method[C]∥International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts. Pergamon: [s. n.], 1993, 30(7): 1411-1417.

[35] HATZOR Y H, BENARY R. The stability of a laminated voussoir beam: back analysis of a historic roof collapse using DDA[J]. International Journal of Rock Mechanics and Mining Sciences, 1998, 35(2): 165-181.

[36] KIM Y I, AMADEI B, PAN E. Modeling the effect of water, excavation sequence and rock reinforcement with discontinuous deformation analysis[J]. International Journal of Rock Mechanics and Mining Sciences, 1999, 36(7): 949-970.

[37] THOMAS P A, BRAY J D. Capturing nonspherical shape of granular media with disk clusters[J]. Journal of Geotechnical and Geoenvironmental Engineering, 1999, 125(3): 169-178.

[38] KAMAI R, HATZOR Y H. Numerical analysis of block stone displacements in ancient masonry structures: A new method to estimate historic ground motions[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2008, 32(11): 1321-1340.

[39] DONG X, WU A Q, REN F. A preliminary application of discontinuous deformation analysis (DDA) to the three gorges project on Yangtze River, China[C]∥Proceedings of the First International Forum on Discontinuous Deformation Analysis (DDA) and Simulations of Discontinuous Media. Berkeley: [s. n.], 1996: 310-317.

[40] ZHU W, ZHANG Q, JING L. Stability analysis of the ship-lock slopes of the Three-Gorge project by three-dimensional FEM and DEM techniques[C]∥Proceedings of the Third International Conference of Discontinuous Deformation Analysis (ICADD-3). Alexandria: American Rock Mechanics Association (ARMA), 1999: 263-272.

[41] KOTTENSTETTE J T. DDA analysis of the RCC modification for Pueblo Dam[C]∥Proceedings of Third International Conference on Analysis of Discontinuous Deformation-From Theory to Practice. [S. l]: Vail Co., 1999: 3-4.

[42] LAW H K, LAM I P. Evaluation of seismic performance for tunnel retrofit project[J]. Journal of Geotechnical and Geoenvironmental Gngineering, 2003, 129(7): 575-589.

[43] SCHELDT T, LU M, MYRVANG A. Numerical analysis of Gjovik cavern: a comparison of continuous and discontinuous results by using Phase 2 and DDA[C]∥Fifth International Conference on Analysis of Discontinuous Deformation-Stability of Rock Structures. Rotterdam: Balkema, 2002: 125-132.

[44] HATZOR Y H, ARZI A A, TSESARSKY M. Realistic dynamic analysis of jointed rock slopes using DDA[C]∥Proc., 5th International Conference on Analysis of Discontinuous Deformation-stability of rock structures. Rotterdam: Balkema， 2002: 47-56.

[45] HATZOR Y H, ARZI A A, ZASLAVSKY Y, et al. Dynamic stability analysis of jointed rock slopes using the DDA method: King Herod’s Palace, Masada, Israel[J]. International Journal of Rock Mechanics and Mining Sciences, 2004, 41(5): 813-832.

[46] 張迎賓,余鵬程,趙興權. 類梯形山體的地震動力響應分析[J]. 西南交通大學學報,2015,3(3): 435-441.

ZHANG Yingbin, YU Pengcheng, ZHAO Xingquan. Analytical solutions of earthquake dynamic responses of trapezoid-like mountain[J]. Journal of Southwest Jiaotong University, 2015, 3(3): 435-441.

[47] 殷躍平. 汶川八級地震地質災害研究[J]. 工程地質學報,2008,16(4): 433-444.

YIN Yueping. Researches on the geo-hazards triggered by Wenchuan Earthquake, Sichuan[J]. Journal of Engineering Geology, 2008, 16(4): 433-444.

[48] 許強. 汶川地震大型滑坡研究[M]. 科學出版社,2009: 53-91.

[49] 黃潤秋,裴向軍,李天斌. 汶川地震觸發大光包巨型滑坡基本特征及形成機理分析[J]. 工程地質學報,2008,16(6): 730-741.

HUANG Runqiu, PEI Xiangjun, LI Tianbin. The basic characteristics and formation mechanism of Daguangbao large-scale landslide triggered by Wenchuan Earthquake[J]. Journal of Engineering Geology, 2008, 16(6): 730-741.

[50] 黃潤秋,裴向軍,張偉鋒,等. 再論大光包滑坡特征與形成機制[J]. 工程地質學報,2009,6(6): 725-736.

HUANG Runqiu, PEI Xiangjun, ZHANG Weifeng, et al. Further examination on characteristicsand formation mechanism of Daguangbao landslide[J]. Journal of Engineering Geology, 2009, 17(6): 725-736.

[51] HUANG R, PEI X, FAN X, et al. The characteristics and failure mechanism of the largest landslide triggered by the Wenchuan earthquake, May 12, 2008, China[J]. Landslides, 2012, 9(1): 131-142.

[52] ZHANG Y B, WANG J M, XU Q, et al. DDA validation of the mobility of earthquake-induced landslides[J]. Engineering Geology, 2014, 194: 38-51.

[53] 程強,蘇生瑞. 汶川地震崩塌滾石坡面運動特征[J]. 巖土力學, 2014,35(3): 772-776.

CHENG Qiang, SU Shengrui. Movement characteristics of collapsed stones on slopes induced by Wenchuan earthquake[J]. Rock and Soil Mechanics, 2014, 35(3): 772-776..

[54] 袁志輝. 延長縣崩塌的數值模擬和運動機理研究[D]. 西安:長安大學,2008.

[55] 崔芳鵬,胡瑞林,殷躍平,等. 縱橫波時差耦合作用的斜坡崩滑效應離散元分析—以北川唐家山滑坡為例[J]. 巖石力學與工程學報,2010,29(2): 319-327.

CUI Fangpeng, HU Ruilin, YIN Yueping, et al. Discrete element analysis of collapsing and sliding response of slope triggered by time difference coupling effects of P and S seismic waves-taking Tangjiashan landslide in Beichuan county for example[J]. Chinese Journal of Rock Mechanics and Engineering, 2010, 29(2): 319-327.

[56] 胡卸文,顧成壯,牛彥博,等. 蘆山地震觸發大巖崩滑坡-碎屑流特征與運動過程[J]. 西南交通大學學報,2013,48(4): 590-598.

HU Xiewen, GU Chengzhuang, NIU Yanbo, et al. Debris flow characteristics and movement process of dayanbeng landslide in tianquan county triggered by“4·20” lushan earthquake[J]. Journal of Sowthwest Jiaotong University, 2013, 48(4): 590-598.

[57] 邱燕玲,姚令侃,朱穎,等. 高烈度地震山區鐵路減災選線技術[J]. 西南交通大學學報,2014, 49(6): 972-980.

QIU Yanling, YAO Lingkan, ZHU Yin, et al. Disaster reduction techniques of railway route selection in mountainous regions with high earthquake intensity[J]. Journal of Southwest Jiaotong University, 2014, 49(6): 972-980.

[58] YIN Y, WANG F, SUN P. Landslide hazards triggered by the 2008 Wenchuan earthquake, Sichuan, China[J]. Landslides, 2009, 6(2): 139-152.

[59] CHEN G, ZEN K, ZHENG L, et al. A new model for long-distance movement of earthquake induced landslide[C]∥44th US Rock Mechanics Symposium and 5th US-Canada Rock Mechanics Symposium. [S. l.]: American Rock Mechanics Association, 2010: 1-6.

[60] YU Pengcheng, ZHANG Yingbin, JOHN X.Zhao, et al. Interaction forces between blocks in DDA method and its application[C]∥12th International Conference on Analysis of Discontinuous Deformation. Wuhan: [s. n.], 2015: 1-8.

[61] 胡卸文,林晉輝,張茂淳,等. 寶興縣城周邊4·20蘆山強烈地震地質災害觸發效應[J]. 西南交通大學學報,2013,48(4): 599-608.

HU Xiewen, LIN Jinhui, ZHANG Maochun, et al. Trigger effect of earthquake geohazards around baoxing county induced by lushan 4·20 strong earthquake[J]. Journal of Southwest Jiaotong University, 2013, 48(4): 599-608.

[62] CHEN G, ZHENG L, ZHANG Y, et al. Stability analysis of breakwater under seepage flow using DDA[C]∥ASME 2013 32nd International Conference on Ocean, Offshore and Arctic Engineering. American Society of Mechanical Engineers. Nantes: [s. n.], 2013: V006T10A035-V006T10A035.

[63] CHEN G, ZHENG L, ZHANG Y. Practical applications of DDA to disaster prevention[M]. Fukuoka: [s. n.], 2013: 15-28.

[64] DONG S, ZEN K, KASAMA K, et al. Theoretical and experimental study on tsunami induced instability of casisson type composite breakwater[J]. Memoirs of the Faculty of Engineering, Kyushu University, 2012, 72(2): 55-68.

趙興權(1958—),博士,2011年起至今任職于西南交通大學,現為土木工程學院教授,博士生導師.主要研究方向為復雜地區地震動衰減關系、地震場地及地貌效應與特殊結構地震反應、地震動特性對結構反應的影響、地震作用下高鐵列車安全運營.2011年獲中組部“千人計劃”和四川省“百人計劃”特聘專家(全職).在國際重要刊物和重要國際會議上累計發表論文80余篇,國際一流SCI收錄論文30余篇,主持多項重大國際項目.提出了國際認同的地震動衰減模型,并被美國、日本、歐洲、加勒比海、東南亞和南太平洋等多個國家和地區廣泛應用.

E-mail: johnzhao1000@126.com

張迎賓(1983—),博士,2013年起至今任職于西南交通大學，現為土木工程學院副教授、碩士生導師.主要研究方向為DDA、NMM程序開發和應用、地震邊(滑)坡破壞機制及運動特征、二維及三維邊坡穩定性分析方法、巖土工程極限分析.發表學術論文60余篇,其中，SCI收錄21篇,EI收錄36篇,包括在巖土工程領域國際權威期刊CGJ、ENGEO、IJRMMS、SODYN、COGE等發表的論文.主持多項國家、省部級科研項目.擔任10余本巖土工程領域知名SCI期刊的審稿人.

E-mail: yingbinz516@126.com

(中文編輯:秦 瑜 英文編輯:蘭俊思)

Discontinuous Deformation Analysis Method and Its Applications to Disaster Prevention

ZHAOXingquan1,ZHANGYingbin1,CHENGuangqi2,YUPengcheng1,HUAGNXiaofu1,CHENYanyan1

(1. School of Civil Engineering, Southwest Jiaotong University, Chengdu 610031, China; 2. Department of Civil and Structure Engineering, Kyushu University, Fukuoka 819-0395, Japan )

In order to explore the characteristics of geological hazards induced by earthquake, the discontinuous deformation analysis (DDA) was used to simulate the failure processes of rock collapses, landslides, and breakwaters under the earthquake loading. Particularly, the influence of the earthquake loading on hazard processes and motions was studied, and new modules were integrated into the current DDA code to obtain the interaction forces. The results show that DDA can be applied to evaluation of landslide mass mobility. The vertical ground motion can remarkably amplify the mobility in the near-fault area. DDA has advantage in the whole-process simulation of landslide induced by earthquake. The simulation results can reflect the characteristics of the failure processes of collapses, landslides and breakwaters faithfully. In addition, DDA is also able to calculate the impact force of failure masses on structures. The peak value of the impact force is much larger than the static lateral pressure, and is four times more than the static lateral pressure in the case study. Hence, the DDA can provide technical guidance for site selection and design of disaster protection from the perspective of reliability and economy.

DDA; earthquake; geological hazards; disaster prevention and control

2015-11-02

國家自然科學基金資助項目(51408511); 中央高校2015年度科技創新項目(2682015CX080); 第48批教育部留學回國啟動基金資助項目.

趙興權,張迎賓,陳光齊,等. 非連續變形分析方法及其在災害防治研究中的應用[J]. 西南交通大學學報,2016,51(2): 300-312.

0258-2724(2016)02-0300-13

10.3969/j.issn.0258-2724.2016.02.010

P642.22

A