助推-滑翔式導彈總體參數設計方法初探

蔣明明，袁慶航，趙長見，卜奎晨

（中國運載火箭技術研究院，北京，100076）

助推-滑翔式導彈總體參數設計方法初探

蔣明明，袁慶航，趙長見，卜奎晨

（中國運載火箭技術研究院，北京，100076）

以兩級固體推進劑火箭發動機助推、彈頭直接入軌，而后全程在大氣層內滑翔飛行的助推-滑翔式導彈為研究對象，對導彈總體參數設計進行研究，給出一種適用于助推-滑翔式導彈的總體參數設計方法。根據助推-滑翔式導彈的彈道特點，通過分段分析彈道特性，推導出導彈總體參數與關機點理想速度間的關系式。通過仿真分析，建立滑翔起點參數與關機點參數間的關系模型；考慮平衡滑翔條件，得到滑翔射程公式。基于以上公式和模型，給出助推-滑翔式導彈射程與關機點參數之間的解析關系，初步建立了助推-滑翔式導彈總體參數的設計方法。

助推-滑翔式導彈；武器裝備；總體參數設計

0 引 言

助推-滑翔式導彈是一種利用火箭助推，彈頭在大氣層內靠氣動升力進行滑翔飛行的導彈武器。助推-滑翔式導彈結合了彈道導彈與巡航導彈的優點，可以實現大氣層內高超聲速飛行，實現遠距離精確打擊，具有強機動能力和突防能力，是目前世界主要軍事大國導彈武器研究的主要方向。助推-滑翔式彈道的概念早在1933年就已經被提出，但由于科學技術發展水平的限制，基于這種彈道的高超聲速滑翔飛行器一直處于驗證階段。近年來，以美國和俄羅斯為代表的主要軍事大國正加緊驗證助推-滑翔式飛行器的關鍵技術，并列入武器裝備研究計劃。

導彈總體參數的設計是導彈設計的基礎，在方案論證階段快速獲得總體參數將有助于提高總體設計效率、縮短設計周期。文獻[1]推導出了彈道式飛行器的航程公式；文獻[2]推導出了單級彈道式飛行器、高超聲速助推-滑翔式飛行器及高超聲速助推-巡航飛行器的起飛質量與射程、推進劑比沖和載荷之間的解析關系；文獻[3]通過引入射程經驗公式并進行近似質量分析，將求解固體彈道導彈最優級間比轉化為求解各子級推進劑質量比之間的關系，以最小起飛質量為優化目標，求得了n級導彈各級最佳推進劑質量比；文獻[4]以導彈起飛質量最小為目標，對導彈質量進行近似分析，并忽略速度的阻力損失以及噴管出口壓力損失，將求解n級液體彈道導彈最優總體設計參數轉化為求解各級最優推進劑質量比和推重比，獲得了可行的理論解法。

目前，助推-滑翔式導彈的總體參數設計尚未有系統的理論方法。本文根據助推-滑翔式導彈的彈道特點，對其彈道進行分段研究，得到導彈射程與關機點參數之間的解析關系，初步建立了助推-滑翔式導彈總體參數的設計方法，并通過設計實例驗證此方法的可行性，為此類型導彈的總體參數設計提供了參考。

1 助推-滑翔式導彈總體參數設計方法

根據助推-滑翔式導彈的彈道特點，將其彈道分為助推段、無動力下壓段、拉起段、滑翔段及下壓攻擊段，如圖1所示。

在助推-滑翔式導彈的彈道中，滑翔段射程占導彈射程的絕大部分，助推段及下壓攻擊段射程占導彈射程比例較小，解析分析時可以忽略這2段對導彈全射程的影響。

1.1 導彈總體參數與關機點理想速度的解析關系

雖然助推段射程對于導彈全射程的影響很小，但其彈道特性直接決定了關機點參數，對導彈的射程及飛行控制等均有較大影響。因此，本節以兩級固體導彈為例，研究導彈起飛質量等總體設計參數與關機點理想速度間的關系，為建立助推-滑翔式導彈總體參數設計方法打下基礎。

引入發動機質量比σ1和σ2，導彈各級起飛質量可表示為

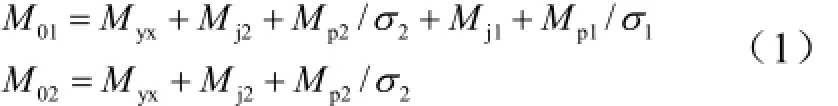
式中 Myx為有效載荷即彈頭質量；M01和M02分別為導彈一、二級起飛質量；Mp1和Mp2分別為導彈一、二級推進劑質量；Mj1和Mj2分別為導彈一、二子級結構質量。

根據齊奧爾科夫斯基公式，兩級導彈二級發動機關機時刻的理想速度Vk1為

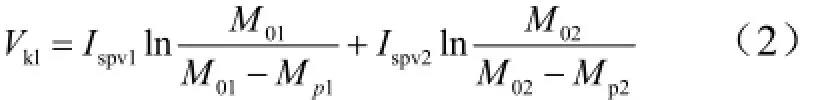
式中 Ispv1和Ispv2分別為導彈一、二級真空比沖。

引入有效推進劑質量比μki= Mpi/M0i，則有：

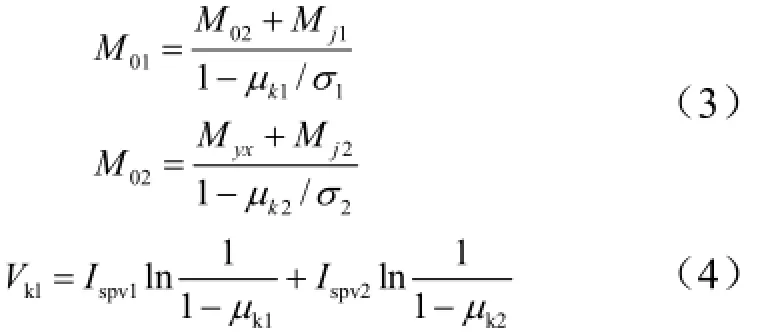
這是一個求函數條件極值的問題：Vk1給定的情況下，求M01為最小時的參數μk1和μk2。即為求下述拉格朗日函數無條件極值的問題：

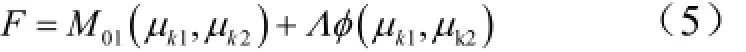
式中 Λ為待定拉格朗日乘子；φ 為約束條件：

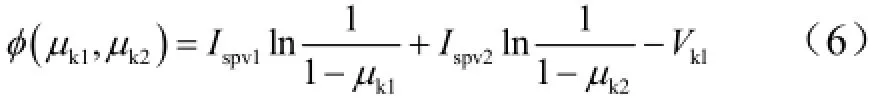
令Myx+Mj2= a，Mj1= b，Ispv2/Ispv1= c，經計算得：

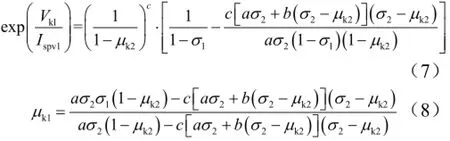
在得到Vk1之后，可由式（7）求得二級有效推進劑質量比μk2，再將μk2帶入式（8），即可求得一級有效推進劑質量比μk1。之后，即可計算Mp1和Mp2等參數，從而確定出導彈最優起飛質量。

通過計算驗證公式推導的正確性計算條件如下：

a）Vk1= 4000 m/s，有效載荷（即彈頭）質量為1600 kg；

b）Ispv1= 2600 (N·s)/kg，Ispv2= 2800 (N·s)/kg；

c）Mj1= 500 kg，Mj2= 200 kg。

導彈起飛質量與二級有效推進劑質量比、發動機質量比的關系曲線如圖2所示。

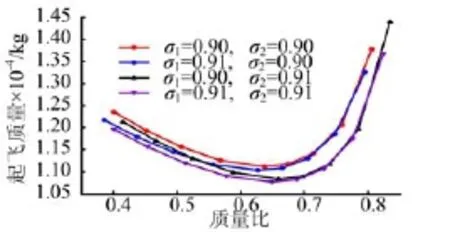
圖2 導彈起飛質量隨有效推進劑質量比變化曲線

從圖2中可以看出，對應不同發動機質量比，均有一個最優二級有效推進劑質量比使得導彈起飛質量最小，且其值與理論值相同，證明了導彈總體參數設計方法的正確性。

1.2 滑翔起點參數與關機點參數的關系

滑翔起點參數包括滑翔起點的速度和射程（即無動力下壓段及拉起段射程之和），下面分別求解這2個參數與關機點速度Vk和關機點當地彈道傾角θk之間的關系。

通過仿真分析，滑翔起點速度值V0與關機點參數近似滿足以下關系：

式中 a2和b2為擬合為kθ的多項式函數。

通過對仿真結果進行擬合，無動力下壓段及拉起段的射程之和L1與關機點參數間近似滿足以下關系：

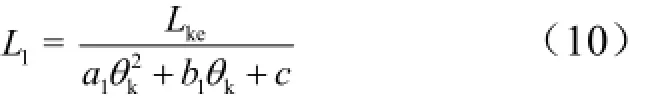
式中 a1，b1，c可以擬合為Vk的多項式函數；Lke為以關機點參數為起點計算出的真空狀態下的拋物線射程，計算公式[5]如下：

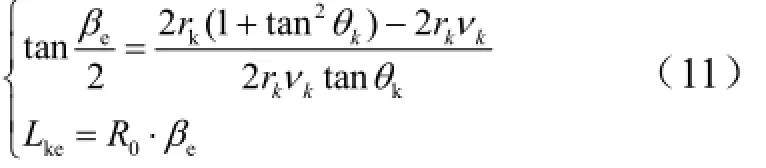
式中 βe為射程角；rk為關機點地心距；νk為關機點能量參數，；μ 為地球引力系數。

1.3 滑翔段射程公式

在進行滑翔段射程分析時，為了簡化問題，對導彈滑翔運動模型作如下假設：

a）不考慮地球旋轉，即ωe= 0；

b）地球為一均質圓球，即引力加速度與地心距平方成正比，g = fM/r2；

c）導彈僅在平面內運動，無滾轉和側滑。導彈滑翔段的運動方程為

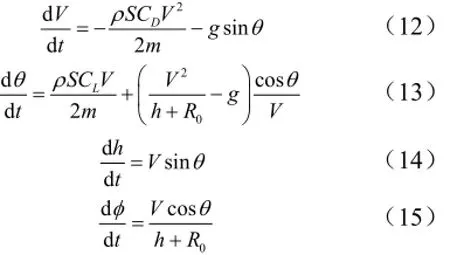
式中 V，θ，h，φ 分別為導彈速度、當地彈道傾角、飛行高度及射程角；R0，ρ，S，m分別為球形地球半徑、大氣密度、導彈參考面積和質量；CL和CD分別為導彈的升力系數和阻力系數。

本文中，滑翔段采用平衡滑翔飛行，平衡滑翔指飛行器在大氣層內無動力飛行時，沿航跡每一點處飛行器所受的升力、重力和離心力平衡，即0θ=˙的狀態。對式（13）進行整理可得平衡滑翔狀態受力關系為

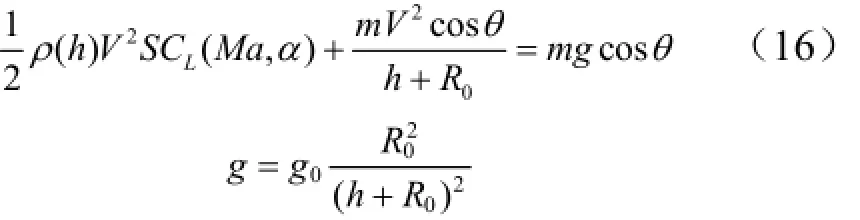
高超聲速飛行器滑翔距離一般在上千公里，而滑翔段高程變化一般小于50 km，因此當地彈道傾角和徑向速度都很小，可以認為θ = 0，代入式（16）中可得：

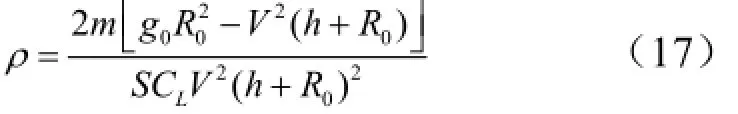
由式（15）除以式（12），并結合平衡滑翔條件，可得平衡滑翔條件下射程角對滑翔速度的偏導數：

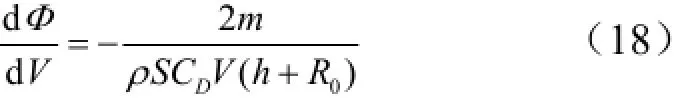
將式（12）代入式（13），并令K = CL/CD，整理可得：

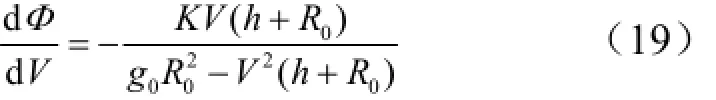
假設平衡滑翔過程中，升阻比K和高度h近似不變，設V0和h0分別為滑翔起始點的速度和高度，對式（19）進行積分，可得平衡滑翔射程角φ 與速度V的關系式：

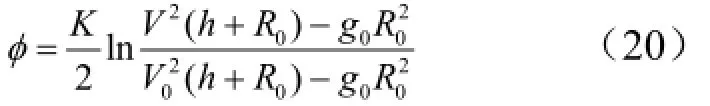
相應的平衡滑翔射程為

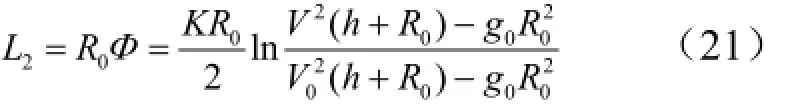
由式（21）建立滑翔距離與升阻比、滑翔高度及滑翔速度的關系。其中，滑翔高度及升阻比均近似為常值，滑翔結束點速度可根據落地點速度約束選定，即平衡滑翔射程僅與滑翔起點速度值有關。

1.4 導彈射程與關機點參數之間的關系

將式（10）和式（21）相加，即可得到助推-滑翔式導彈全射程公式：

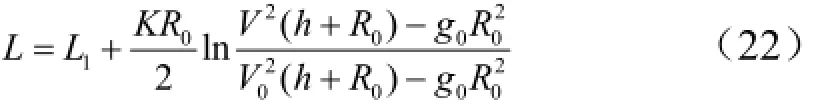
將式（9）及式（10）代入式（22），即建立了助推-滑翔式導彈射程與關機點速度Vk和關機點當地彈道傾角θk間的關系。

1.5 導彈總體參數與射程指標之間的關系

給定射程指標L及式（22）中的各常量后，即可求得助推-滑翔式導彈的關機點參數。之后，即可根據導彈總體參數與關機點理想速度間的解析關系，通過關機點參數求得助推-滑翔式導彈的起飛規模等總體設計參數。

2 仿真算例

技術指標要求：射程1300 km，彈頭質量1600 kg。

一般，助推-滑翔式導彈關機點處當地彈道傾角θk較小，可取θk= 7°，滑翔升阻比K = 2.5，滑翔高度h = 40 km，滑翔結束點速度V = 1000 m/s；導彈一、二子級結構質量分別為500 kg和200 kg；一、二級發動機質量比σ1= σ2= 0.9；一、二級發動機真空比沖分別為Ispv1= 2600 (N·s)/kg，Ispv2= 2800 (N·s)/kg。

根據工程經驗，經大量仿真計算，將a2和b2擬合為θk的五次多項式，a1，b1，c擬合為Vk的三次多項式函數，所得擬合結果較為理想。

由式（10），得到導彈關機點速度：Vk= 3017 m/s。

考慮到實際飛行中存在的速度損失，同時為簡化問題，本文中取速度損失ΔVk= 0.25Vk，則理想速度：Vk1= Vk+ΔVk= 1.25Vk= 3771 m/s。

根據助推-滑翔式導彈總體參數設計方法，計算得到助推-滑翔式導彈總體參數為μk1= 0.32；μk2= 0.63；M01= 10 017 kg；M02= 5 964 kg。

為驗證助推-滑翔式導彈總體參數設計方法的可行性，基于上述總體參數進行助推-滑翔式彈道的數學仿真驗證。取一級真空推力P1= 280 kN，二級真空推力P2= 200 kN，并進行彈道仿真，仿真結果如圖3所示。

仿真所得導彈落速為560 m/s，當地彈道傾角為-80°，導彈射程為1250 km，與設計指標間的誤差為3.8%，由此可見，本文得到的助推-滑翔式導彈總體參數設計方法可以用于方案論證初期的導彈總體參數選擇。

Preliminary Investigation of Parameter Design Method for Boost-Glide Missile

Jiang Ming-ming, Yuan Qing-hang, Zhao Chang-jian, Bu Kui-chen
(China Academy of Launch Vehicle Technology, Beijing, 100076)

Based on two class solid propellant missile whose warhead orbits directly and then glides in the aerosphere all along, missile parameter design is studied, and a parameter design method for boost-glide missile is proposed. According to the characteristic of boost-glide trajectory, the trajectory is divided into several parts and each part is studied: the relationship between missile parameters and the theoretical velocity is deducted; through simulation, the model used to describe the relationship between parameters of glide starting point and that of engine shutdown point is established; considering the balanced glide condition, the formula to estimate the glide range is obtained. Based on the models, the analytical expression between the missile range and the parameters of the engine shutdown point is given, and the parameter design method for glide missile is established preliminarily.

Boost-glide missile; Weaponry and equipment; Parameter design

V421.1

A

1004-7182(2016)04-0005-04

10.7654/j.issn.1004-7182.20160402

2015-01-06；

2015-02-13

蔣明明（1990-），男，助理工程師，主要研究方向為飛行器設計