基于自適應進化相關向量機的城市需水量預測模型研究
徐繼紅
(新疆塔里木河流域管理局, 新疆 庫爾勒 841000)
?
基于自適應進化相關向量機的城市需水量預測模型研究
徐繼紅
(新疆塔里木河流域管理局, 新疆 庫爾勒841000)
【摘要】為改進城市需水量預測模型,將相關向量機與差分進化優化算法進行融合及改進,提出基于自適應進化相關向量機的需水量預測模型。以新疆阿克蘇市為例,建立基于自適應進化相關向量機的城市需水量預測模型,并與多元線性回歸、BP神經網絡、支持向量機算法在精度與可靠性方面進行對比分析。結果表明:新模型預測精度大約是上述其他方法的2倍以上; 測試數據的實際需水量均在自適應進化相關向量機估計的95%置信度的置信區間內,并且由后驗差比、小誤差概率判定模型等級屬于“好”級別。
【關鍵詞】城市需水量; 預測; 自適應進化; 相關向量機
隨著城市對水資源需求的日益提高,對城市需水量進行科學的分析和預測是滿足城市發展需求、保證水資源可持續利用的前提。因此,如何構建城市需水量與其驅動力之間復雜的函數模型、預測需水量變化成為當今水資源規劃利用的熱點問題。當前,傳統需水量預測模型主要包括線性回歸模型、時間序列分析、灰色理論等[1-2]。但這些模型未充分綜合考慮社會、自然與經濟等復雜影響因素對需水量變化的影響,導致擬合精度不高。隨著神經網絡及元胞自動機等人工智能算法的提出,人工智能、機器學習(如SVM)等方法的應用,預測精度較傳統方法有較大提高。但這些方法重點集中在預測精度提高方面,對算法稀疏化及預測結果的不確定性分析很少,研究稀疏化和具有概率意義的城市需水量預測模型對提高模型精度及結果可靠性具有重要意義。
相關向量機[3- 4]是一種貝葉斯框架下的稀疏概率模型,該算法在具有稀疏性的同時可獲得預測結果的不確定性信息,且算法待定參數少,核函數不受Mercer條件限制。這在解決諸多模式識別和回歸估計的實際問題中取得了良好效果,但在城市需水量預測方面未見相關研究。因此,本文將該算法應用于需水量預測,并將全局搜索能力強、魯棒性好與收斂速度快的自適應差分進化算法[5]與相關向量機結合,優化相關向量機待定參數,提出基于自適應進化相關向量機的城市需水量預測模型。以新疆阿克蘇市需水量預測為例,分析基于自適應進化相關向量機的預測模型建立過程,并與多種需水量預測方法進行對比分析,證明本文方法在模型精度、可靠性及稀疏性方面的優點,以期為相關向量機進一步研究應用提供參考。
1自適應進化相關向量機模型
本文利用自適應差分進化算法自適應確定相關向量機待定參數,提出自適應進化相關向量機模型(self-adaptive differential evolution-relevance vector machine,SADE-RVM),以提高模型預測精度。
1.1自適應差分進化算法構建
差分進化算法(differential evolution,DE)是一種基于實數編碼的群體智能理論的優化算法,算法原理類似于遺傳算法[6]。通過群體內個體間的合作與競爭產生的群體智能指導優化搜索,因此該算法有更好的全局搜索能力、魯棒性與收斂速度。該算法通過對種群中的個體進行變異、交叉、選擇操作,獲得最優個體,確定最優值。鑒于算法的縮比因子F和交叉概率Cr參數對算法影響較大,本文構建F與Cr參數自適應的DE算法(self-adaptive differential evolution,SADE)[7],算法工作原理如下:
a.變異操作。對n代m個體vm(n)進行變異操作,在種群數量范圍內隨機選取不同r1、r2、r3號vr1(n)、vr2(n)、vr3(n)按照式(1)進行變異操作,產生n+1代個體vm(n+1)。
(1)
b.交叉操作。對個體vm(n)與個體vm(n+1)的d的維數按照式(2)進行交叉,產生個體um(n+1)。Cr為交叉概率,k為在1與最大維數之間隨機產生的整數,保證至少有一維數進行交叉。
(2)
c.選擇操作。以適應度大小為個體優劣判定依據,對個體vm(n)與um(n+1)進行選擇,優選個體加入下一代種群。
針對F、Cr參數對算法性能影響較大這一問題,依據當前個體適應與最大、最小適應度之間關系采取策略式(3)、式(4)對參數進行自適應調整,提高算法可靠性。
(3)
(4)
式中Fmax、Fmin——最大、最小縮比因子;
Crmax、Crmin——最大、最小交叉概率;
fmax(n)、fmin(n)——n代最大、最小適應度;
fm——m個體適應度。
1.2模型構建
根據SADE與RVM算法特點,以留一交叉驗證法建立SADE算法的適應度函數[8],自適應確定RVM模型最優參數,提出SADE-RVM模型,減少人為參數確定不當對RVM算法性能的不利影響。
1.3模型精度評價方法
為對模型精度進行合理評價,選取3種預測模型進行對比分析。建立定量與定性的模型精度評價指標,對自適應進化向量機模型精度做出科學、合理的評價。
a.對比模型的建立。選取多元線性回歸、BP神經網絡、最小二乘支持向量機作為對比模型,分別建立預測模型,以Matlab編程實現,具體建模過程如下:?多元線性回歸模型(multivariate linear regression,MLR):以影響需水量變化的7種因素為模型輸入、城市需水量為模型輸出,以regress函數求解模型參數,建立多元線性回歸預測模型;?BP神經網絡:以影響需水量變化的7種因素為模型輸入、需水量為模型輸出,1個隱含層、6個神經元,傳遞函數包括{‘logsig’,‘tansig’},以trainlm函數為訓練函數,建立基于BP神經網絡的預測模型;?最小二乘支持向量機(least squares support vector machine,LS-SVM):以影響需水量變化的7種因素為模型輸入、需水量為模型輸出,選擇徑向基核函數作為算法核函數,以網格搜索法通過多次試算,確定最小二乘支持向量機的2個參數,建立預測模型。
b.模型精度評價方法。選取平均絕對誤差(mean absolute error,MAE)、平均相對誤差(mean relative error, MRE)、均方根誤差(root mean square error,RMSE)3個精度指標評價各模型精度優劣。
根據后驗差比C及小誤差概率P[9]對需水量變化預測模型精度進行等級劃分,對各預測模型進行定性評價,具體見表1。
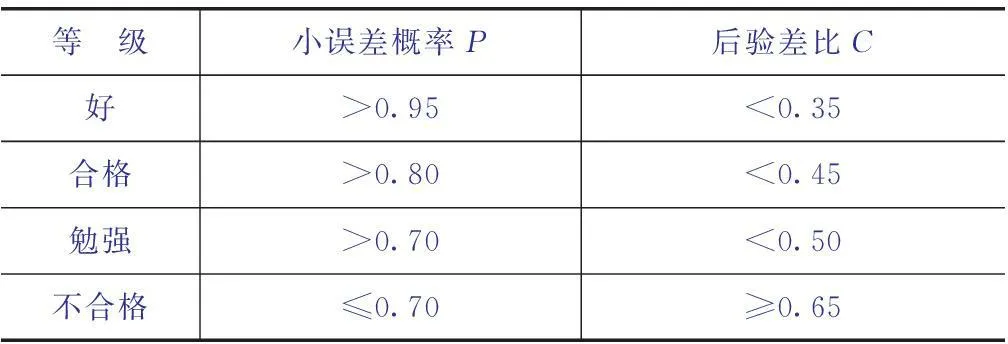
表1 城市需水量預測模型精度等級劃分
2模型應用
本文以新疆阿克蘇市城市需水量變化為例,建立自適應進化預測模型。
2.1建模數據源
城市需水量變化受社會、自然、經濟等方面的多種因素影響,通過參考《阿克蘇市統計年鑒》[10-11],收集該市1990—2005年城市需水量(y)及其影響因素數據(見表2)。由于各變量單位不同,對建模精度有較大影響。因此,需對原始數據進行歸一化處理后才可用于模型建立。表2中,x1為GDP(萬元),x2為人均GDP(元),x3為固定資產投資(萬元),x4為工業個數(個),x5為城市人口(萬人),x6為供水總量(萬m3),x7為人均日生活用水量(L/d),y為城市需水量(萬m3)。
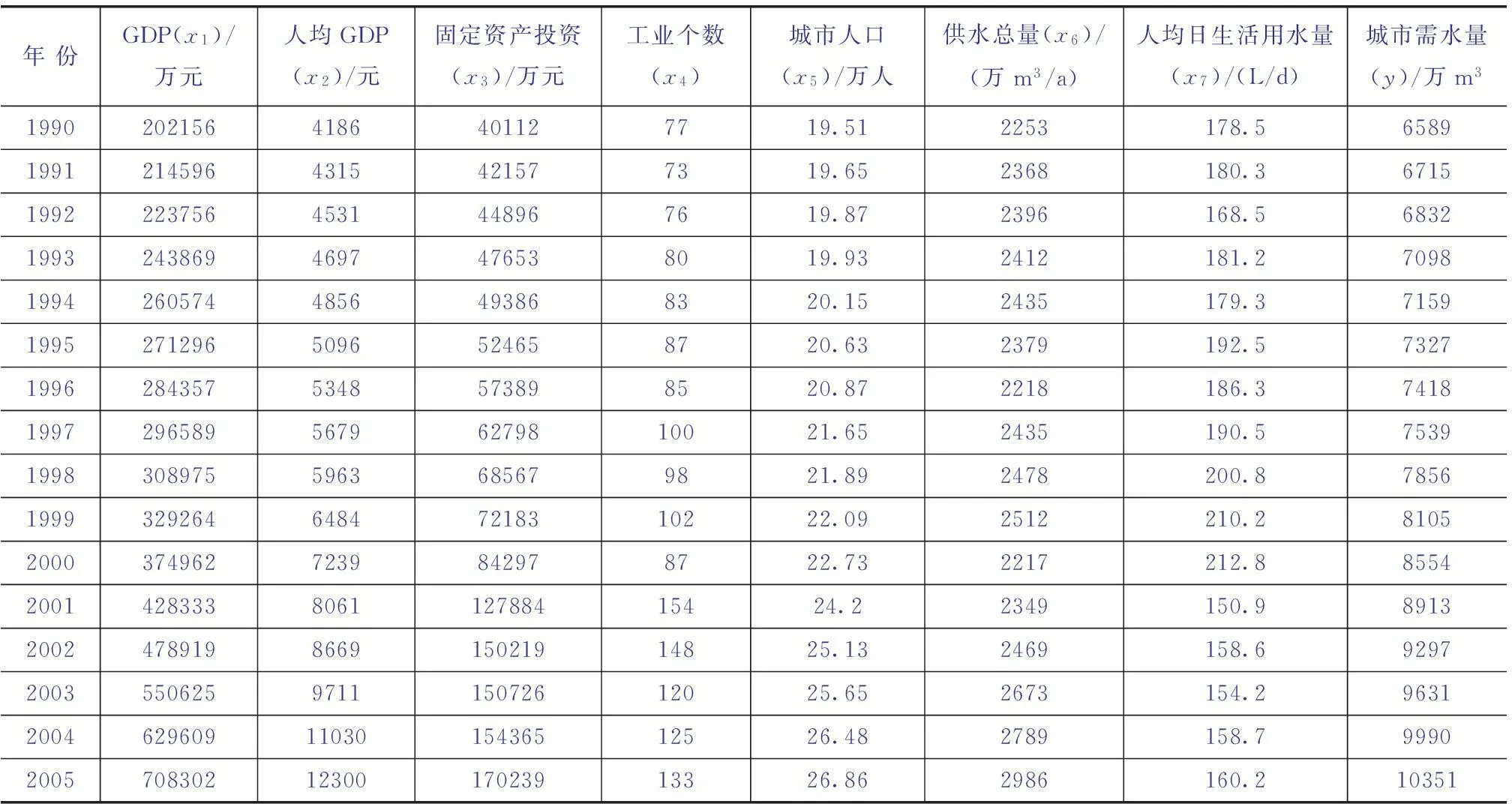
表2 阿克蘇市1990—2005年需水量及其影響因子
2.2預測模型構建
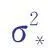
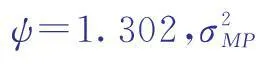
2.3結果評價
將測試數據集輸入預測模型,預測2001—2005年需水量,同時建立95%置信度的置信區間[12]。為評價自適應進化相關向量機對需水量預測的精度,基于多元線性回歸、BP算法、LS-SVM建立需水量預測模型。各模型預測結果見表3。
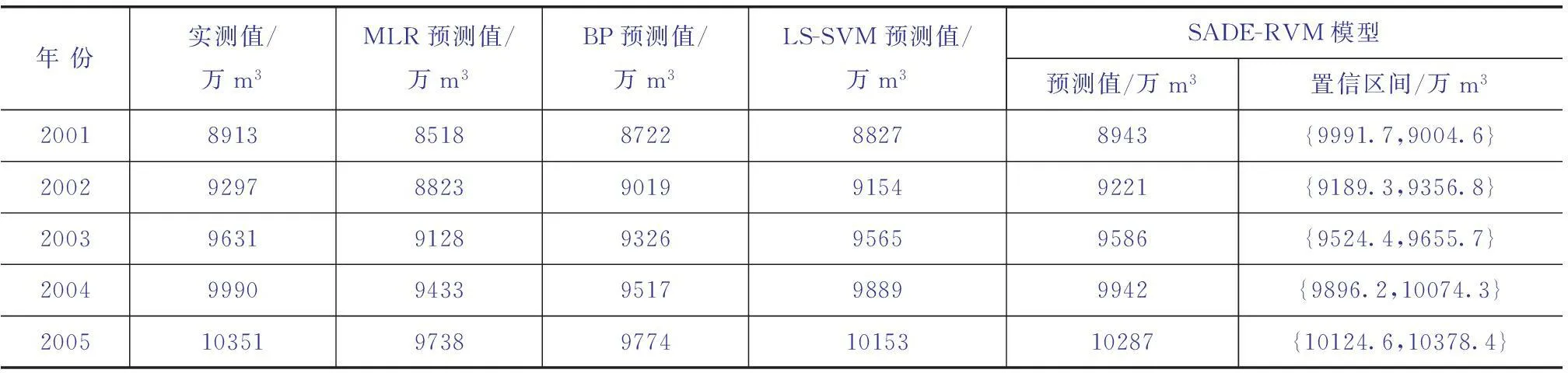
表3 需水量預測值和實測值
基于以上數據,計算各預測模型的MAE、MRE、RMSE、后驗差比C、小誤差概率P、模型等級等評價指標,具體結果見表4。

表4 預測模型評價指標
表3表明:2001—2005年需水量實際值均在自適應進化相關向量機估計的95%置信度區間內,證實預測結果可靠。由表4可知:自適應進化相關向量機各項精度指標表現最優,模型等級屬于“好”,證實本文提出的新方法具有很高的預測精度。建立自適應進化相關向量機的城市需水量預測模型時,11組訓練數據中只有3組為相關向量最終參與預測模型構建,有效簡化了模型復雜度,具有很高的稀疏性。基于以上分析數據,自適應進化相關向量機的預測方法計算精度高、可靠性強。
3結論
a.本文提出的自適應進化相關向量機模型有效地解決了核函數參數確定問題,自適應優化核函數參數,可降低由于參數不當對模型精度的影響。
b.由MAE、MRE、RMSE數據可知:對于城市需水量預測,自適應進化相關向量機的精度大約是LS-SVM方法的2倍、BP網絡的7倍、多元線
性回歸的10倍。因此,自適應進化相關向量機對城市需水量預測有很高精度。
c.城市需水量實際值均在自適應進化相關向量機估計的置信區間內,定量地證實模型具有很強的可靠性。通過后驗差比、小誤差概率分析,自適應進化相關向量機對需水量預測結果等級屬于“好”,定性地證實該模型具有很好的預測效果。
參考文獻
[1]宓永寧,陳默,張茹.灰色拓撲法在大伙房水庫總氮預測中的應用[J].水利建設與管理,2009(3):72-73.
[2]江智健.清華水電站直供電片區電力需求預測及其啟示[J].中國水能及電氣化,2013(10):45- 49.
[3]Tipping M E.Sparse bayesian learning and the relevance vector machine[J]. Journal of Machine Learning Research 2001,1(3):211-244.
[4]Bishop C M,Tipping M E.Variational relevance vector machine[C]//The 16th Conf on Uncertainty in Artificial Intelligence.USA:Morgan Kaufmann,2000.
[5]Storn R,Price K.Differential evolution:A simple and efficient beuristic for global optimization over continuous spaces[J].Journal of Global Optimization,1997,11(4):341-359.
[6]Price K,Storn R,Lampinen J.Differential evolution:A practical approach to global optimization[M].Berlin Heidelberg:Springer,2005.
[7]孫昌躍,劉德順,段凱.基于差分進化算法的鉆頭波阻辨識研究[J].煤炭學報,2012,37(2):350-355.
[8]劉學藝,李平,郜傳厚.極限學習機的快速留一交叉驗證算法[J].上海交通大學學報,2011,45(8):1140-1146.
[9]陳懷錄,馮東海.土地利用規劃耕地預測方法對比研究——以甘肅省臨夏市為例[J].西北師范大學學報:自然科學版,2011,47(1):99-104.
[10]阿克蘇地區統計局.阿克蘇統計年鑒[Z].1990-2002.
[11]阿克蘇地區行署辦公室,阿克蘇地區統計局.阿克蘇統計年鑒[Z].2003-2005.
[12]Wang F F,Zhang Y R.Relevance vector machine technique for the inverse scattering problem[J].Chinese Physics B,2012,21(5):19-24.
Research on urban water demand forecast model based on adaptive evolution relevance vector machine
XU Jihong
(XinjiangTarimRiverBasinAdministration,Korla841000,China)
Abstract:The relevance vector machine and differential evolution optimization algorithm are converged and improved in order to improve urban water demand forecast model. Water demand forecast model based on adaptive evolution relevance vector machine is proposed. Aksu in Xinjiang is adopted as an example. Urban water demand forecast model based on adaptive evolution relevance vector machine is established. It is comparatively analyzed with multiple linear regression, BP neural network and support vector machine algorithm in terms of accuracy and reliability. The results show that new model forecast accuracy is about more than 2 times compared with other above-mentioned methods. Actual water demand of test day is in the confidence level of 95% confidence estimated by adaptive evolution relevance vector machine. It is determined that the model level belongs to ‘good’ level through posteriori difference ratio and small error probability.
Key words:urban water demand; forecast; adaptive evolution; relevance vector machine
中圖分類號:TV214
文獻標志碼:A
文章編號:1005- 4774(2016)01-0045-04
DOI:10.16616/j.cnki.10-1326/TV.2016.01.013

