配額目標約束下區域減排的最優控制率

劉　曉, 王　錚， 鄧吉祥

1 湖南省社會科學院，長沙　410003

2 華東師范大學地理信息科學教育部重點實驗室，上海　200062

3 中國科學院科技政策與管理科學研究所，北京　100190

4 長沙學院，長沙　410006

配額目標約束下區域減排的最優控制率

劉曉1,2, 王錚2,3,*， 鄧吉祥2,4

1 湖南省社會科學院，長沙410003

2 華東師范大學地理信息科學教育部重點實驗室，上海200062

3 中國科學院科技政策與管理科學研究所，北京100190

4 長沙學院，長沙410006

摘要:研究了區域碳排放配額目標給定下，如何確定一個保障經濟平穩增長的最優碳排放控制率問題。提出了一個最優減排率確定的計算流程，并且根據前瞻性原則、人口原則、GDP原則、GDP-人口原則、支付能力原則5種不同的碳排放配額分配原則，確定了中國大部分省市自治區可能的最優減排率。選取5個中國省區上海、山西，湖南、云南以及新疆作為案例地區，在計算得到這些地區的減排率的約束下，分析了在社會福利最大化的情況下各區域分配的配額獲得的經濟增長路徑和能源碳排放路徑。模擬結果發現，中國在各種減排約束下各區域的經濟增長路徑呈階梯式下降的趨勢。能源碳排放呈先升后降的整體趨勢，各個省市自治區要實現2030年后不再增加碳排放。得出各東部省份在GDP原則分配的配額約束下減排控制率最小，西部省份在支付能力原則下減排控制率最小，而中部省份則在人口原則下減排控制率較小。5個原則中前瞻性原則適合中國推進的碳減排配額方法。

關鍵詞：碳減排; 減排控制率; 配額;氣候變化

IPCC AR5繼續強調了全球氣候控制問題，其關鍵是CO2的排放控制，有效方式之一就是碳排放權分配。碳排放權分配會促使各區域努力將其碳排放權限定在該區域的排放目標之下，這需要每年采取一定的減排率來逐步實現。2008年的經濟危機后，一個新的視角產生了：區域的碳減排率控制不能刺激經濟危機發生[1]。因此，只能在經濟最優平穩增長條件下實行碳減排目標，即減排率必須控制在經濟系統的最優平穩增長軌道下，這就是最優減排率問題。

這一問題的原始提法是關于減排率計算。在該領域，國內外的主流研究途徑是建立氣候變化經濟學模型來計算合適的減排率，涌現了大量知名的IAM模型。在IPCC AR5中， IMAGE(Integrated Model to Assess Greenhouse Effect, IMAGE)模型、MERGE模型(Model of Evaluating Region and Global Effects of GHG Reduction Policy, MERGE)、MESSAGE模型(Model of Energy Supply Strategy Alternatives and their General Environmental Impacts, MESSAGE)、POLES模型(Prospective Outlook on Long-term Energy Systems, POLES)等14個氣候變化經濟學模型被用于計算未來碳排放情景下的減排與控制問題。其中，最早的工作是Nordhaus建立了DICE(Dynamic Integrated model of Climate and the Economy)模型[2]，并由Nordhaus，Yang發展為多區域的RICE模型，對區域減排率進行了求解，但沒有考慮平穩增長的問題[3]。Pizer基于DICE模型發展的state-contingent模型，考慮不確性參數，對全球最優CO2的減排率進行了模擬研究[4]。崔麗麗、王錚以經濟子模型、氣候子模型和趨勢子模型組成的CGE模型為基礎，利用不確定性參數對確定我國合理的CO2減排率進行了模擬分析[5]。沈子榮對單位GDP碳減排率的計算方法進行了簡單介紹與比較，在此基礎上對中國單位GDP碳減排率進行了計算與分析，得出采用不變價格和購買力平價的計算方法更為科學[6]。但是這些方法并沒有從經濟平穩增長的角度考慮，更沒有受到碳排放配額的約束。另外，中國一些新的研究雖然對未來碳排放情景進行了分行了分析[7- 8]或是強調了減排的最優化問題[9]或是對經濟增長下的減排目標進行了研究[10]，但是仍然回避經濟平穩增長問題。本文試圖在經濟平穩增長條件下確定減排目標，在此基礎上，作為理論檢驗，本文結合中國大部分區域的減排控制問題作了應用研究。

計算平穩增長下減排目標的最優減排率，首先應計算平穩增長條件下實現減排目標的可能性，以區域平穩增長下未來碳排放需求量的評估模型[11]和Nordhaus的評估模型為基礎[12]，確定碳排放配額分配權，其次，綜合考慮5個碳排放公平分配的原則，對區域的配額進行分配，在各原則分配的配額基礎上，對中國的減排控制率進行計算，以期分析未來的經濟發展過程中，中國大部分省市自治區在不同配額分配原則分配的配額約束下的經濟增長路徑、能源消費路徑以及能源碳排放路徑的變化，以及分析各區域在何種分配原則下差距最小的減排控制率，最后，為中國制定配額分配方案提供決策參考，同時探討區域實行碳減排目標后的減排控制率計算問題。

1模型

1.1區域的碳排放需求

區域是一個經濟體，在考慮能源的條件下，參考Nordhuas構建的含減排控制率的生產函數[2]，一個區域生產函數具有如下形式：

Y(t)=A0evtK(t)α(E(t)(1-μ))1-αL(t)γ0<α,γ<1

(1)

式中，μ為區域給定碳排放量下的減排控制率，當μ=0即無減排情景；Y(t)為區域的社會總產出；K(t)為第t期的各個區域的資本；E(t)為第t期的區域的能源消費μ量；L(t)為第t期的區域的勞動投入；A0evt為區域第t期的技術水平，v為區域的能源強度下降速率;α為區域的資本產出彈性; 能源的產出彈性設為1-α;γ為區域的勞動力的產出彈性。根據能源強度的定義即生產一單位經濟產出所需能源消費量，其定義為

τ=E(t)/Y(t)

(2)

式中，τ表示能源強度，把能源強度的公式代入到生產函數中，則社會總產出Y(t)關于能源強度的函數形式可以表示：

Y(t)=A0evtK(t)α[(1-μ)τ(t)Y(t)](1-α)L(t)γ

(3)

公式進一步化簡成：

(4)

資本積累方程寫為：

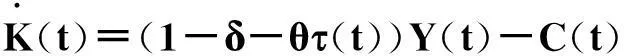
(5)

式中，θ為能源綜合成本，δ為資本折舊率，C(t)為第t期的社會總消費。另外，每個社會成員的效用為人均個人消費c的函數，函數形式為：

(6)

社會計劃者追求的目標是讓社會福利最大化，即社會成員數為N(t) 的效用現值之和為最大：

(7)

加入減排控制率后的改進模型變為以下最優控制問題：

(8)

式中，MQ(t)表示區域的累積碳排放量，MQT表示區域的碳配額量。接下來，由目標函數及狀態方程構造Hamilton函數：

(9)

將(4)式代入到(9)式中得:

(10)

這是系統的Hamilton函數。根據最優控制理論，為獲得(7)定義的拉姆齊函數最大必要條件，必須滿足以下條件：

(11)

即

(12)

(13)

對生產函數式(4)求關于資本偏導，得到如下結果：

(14)

對(12)式兩邊取對數得：

(15)

取(15)式的時間導數得：

(16)

將(14)代入(13)得到：

(17)

將式(16)與式(17)合并得到式(18)：

(18)

當社會實現經濟增長與消費增長平衡即為經濟的平穩增長，于是整理(18)，有保障平穩增長的最優消費增長率為

(19)

令社會總人口為N，勞動參與率為ω，即：就業人口占總人口的比重，n為未來人口平均年增長率。則t年的勞動力與人口分別為：

L(t)=ω(t)N(t)

(20)

N(t)=N0ent

(21)

將它們與式(20)合并，即可整理得保持經濟平穩增長的黃金增長率為：

(22)

式(22)確定的增長率即為人口增長率為n，減排率為μ時的經濟平穩最優增長率。即經濟增長理論所謂的黃金增長率[13]。于是得區域未來經濟平穩增長的經濟總量的期望估計：

Yt=Yt-1(gt+1)

(23)

(24)

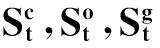
(25)

如果給定區域配額MTQ 則可以找一個減排率μ>0 令MQ(T)=MTQ 成立，即可確定區域在給定配額下的減排率。式(25)即是一個區域內保持經濟平穩增長的碳排放需求。

1.2給定配額下區域最優碳減排變率

區域碳排放不僅受到經濟增長需求的約束，還受區域碳配額的約束。本文在給定區域碳排放配額后，計算了能夠保障區域在碳減排約束下的經濟平穩增長軌道上的最優碳減排率。進一步，由于減排率不可能集中在目標年實現，因此需要ΔY(t)=μY(t-1) 的躍遷，這一躍遷，必然對經濟產生較大的沖擊，因此實際減排過程要求的是讓減排率從0減排逐漸增加，即最初的減排率μ(t=0)=0 逐步變大，最終實現碳減排目標的減排率過程μ(t)，使得(26)式成立：

(26)

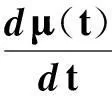
μ(t)=μ0exp(ηt)

(27)

成立。換言之，求最優減排率μ(t) 的問題，轉化為求減排最優減排率的變率問題，我們稱之為最優減排變率。為了求得最優減排變率，把(27)帶入經濟平穩增長的經濟總量(23)，于是以

(28)

為目標，用某種最優化算法，搜索求出給定配額MTQ 下的減排率年變化η，即為最優減排變率，其意義是每年需要以該速度提高碳減排控制率。Ω為減排變率集合，范圍為[0,μ]。其計算流程圖如圖1所示。

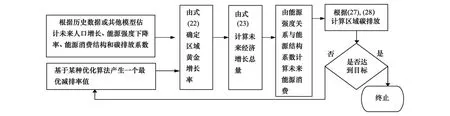
圖1　區域最優減排率計算流程圖Fig. 1　The flow diagram of the optimal carbon emission reduction rate in region

2區域碳減排率的確定

區域碳減排率是由區域碳排放配額確定的，要確定個區域的減排配額，需要先行確定碳配額分配原則。本文根據中國的實際經濟情況，以及1990—2009年累積碳排放量、人口量、GDP量以及計算得到的經濟平穩增長下2010—2050年的GDP、人口以及碳排放需求量等考慮5個分配原則進行分配5個原則控制下，減排率不同各自可能形成若干情景，本文關心的是最優減排率情景。具體5個原則是：

(1)前瞻性原則

前瞻性原則即為根據經濟平穩增長條件下未來各省市自治區的碳排放需求量與全國碳排放總需求量的比例分配碳排放權配額。未來各省市自治區的碳排放需求量根據減排率為0時的黃金增長率，應用式(23)—(28)計算出。前瞻性原則依據未來碳排放需求量來分配碳排放權配額，有利于各區域尤其是經濟較發達的區域在未來的經濟發展過程中保持經濟的連貫性。

(2)人口原則

人口原則即根據經濟平穩增長條件下未來各省市自治區的人口在全國總人口中的比例來分配碳排放權配額。這一原則體現每個人都具有同等利用自然資源的權利，遵循了區域中的每個人對所在區域都享有同等的排放權。理論上，人口原則使得人口較多但是經濟欠發達地區的排放配額較充裕，有利于促進欠發達區域經濟發展，但對人口較少而經濟發展較快的省區形成一定的阻礙。

(3)GDP原則

GDP原則又稱世襲原則，是根據經濟平穩增長條件下未來各區域的GDP量與全國總GDP的比例來分配碳排放權配額。這一原則主要與各區域的經濟發展狀況與趨勢相關，經濟發展較好，經濟總量較大的區域所分配碳排放權配額相對較多。以GDP為原則分配碳排放權配額使得原來相對富裕區域的經濟發展不會因為大幅度減排而影響經濟發展的連續性，從而有利于經濟發展水平高。但對于經濟總量較低的區域，由于所分配的配額量相對較少，且受區位，歷史因素等原因影響，在未來的發展過程中所分配的配額量也較少，從而不利于貧窮地區的發展，導致區域差距擴大。

(4)GDP-人口原則

針對人口原則和GDP原則的優劣，GDP-人口原則是根據經濟平穩增長條件下未來各區域的GDP和人口按相同的權重進行組合，即在人口分配原則和GDP分配原則下分配的配額的基礎上按相同的權重重新分配得到總量。這一原則主要是基于中國大部分省域經濟發展的不平衡性以及人口分布的不均衡性而設定，有助于縮小區域的差距。

(5)支付能力原則

支付能力原則是根據區域經濟水平差異，將區域的減排成本與其經濟狀況聯系，具體是使區域可獲得的碳排放權與人均GDP成反比[14]。支付能力原則可以使得人口規模較大和人均GDP較低的區域分配更多的配額，而人口較少以及人均GDP較高的區域則需承擔更多的減排義務。

作為例子，本文在表1 中給出各種配額原則下中國大部分區域的碳排放強度的最優碳減排變率η，它們構成了相應的減排情景。但是必須強調的是，本文的區域適合于科學意義上的區域(region)是科學學抽象思維。模型可以用于它世界，有可能中國、美國，還可以用于山東、湖南，或者煙臺、曲阜。

某個省市自治區以2010到2050年GDP需求量，人口需求量以及碳排放需求量為基礎，假設2010—2050年國際碳排放權配額分配給中國的總配額量約為75 Gtc，由于總配額量可根據將來國際上最終確定的實際數據進行調節，其最終數字需要修正，但并不影響適合各省域發展的配額原則的選擇。從表1中可以看出，不同配額原則對具體的區域即各個地方減排要求不盡一致。

從表1可以發現，在GDP原則下，東部地區和西部地區的減排下降速率相差較大。其中，東部大部分省份的減排下降速率較小，而西部地區則減排下降速率很大，其中最大的為寧夏，按10.17%的速率下降。可見在GDP原則下要使得西部地區需要更大的下降速率才能累積碳排放量小于配額量。而西部地區在歷史上經濟基礎，自然條件都較差，加大減排速率勢必會導致西部地區經濟總量下降更快，加劇西部地區貧困，擴大東西差距。在人口原則下，內蒙古的減排速率最大，其次為山西，天津，寧夏，遼寧等省。這些省份中內蒙古，山西的能源碳排放量較多，但限于人口因素導致人口分配原則下的配額相對較少，使得配額和未來累積碳排放量之間的差距較大，從而兩省在人口原則下的減排速率較大。而天津，寧夏未來累積碳排放量較小，但同樣由于人口較少在人口原則下分配的配額量遠低于其累積碳排放量，因此，其減排控制率較大。GDP人口原則下各省之間的減排速率相對比GDP原則和人口原則下的減排速率差距小，但是比前瞻性原則下的減排速率大。在支付能力原則，西部地區除內蒙古外，其他省份的減排速率都較小，因此西部地區基本能實現累積碳排放需求量低于支付能力原則下分配的配額量的約束目標。東部地區除海南外大部分省份的減排速率都偏大。這主要是因為在支付能力原則下分配的配額較大，使得累積碳排放需求量與配額的差距較小。

2．血清淀粉酶、脂肪酶測定：采用比色法檢測淀粉酶、脂肪酶，試劑盒購自南京建成生物工程研究所，按說明書操作。

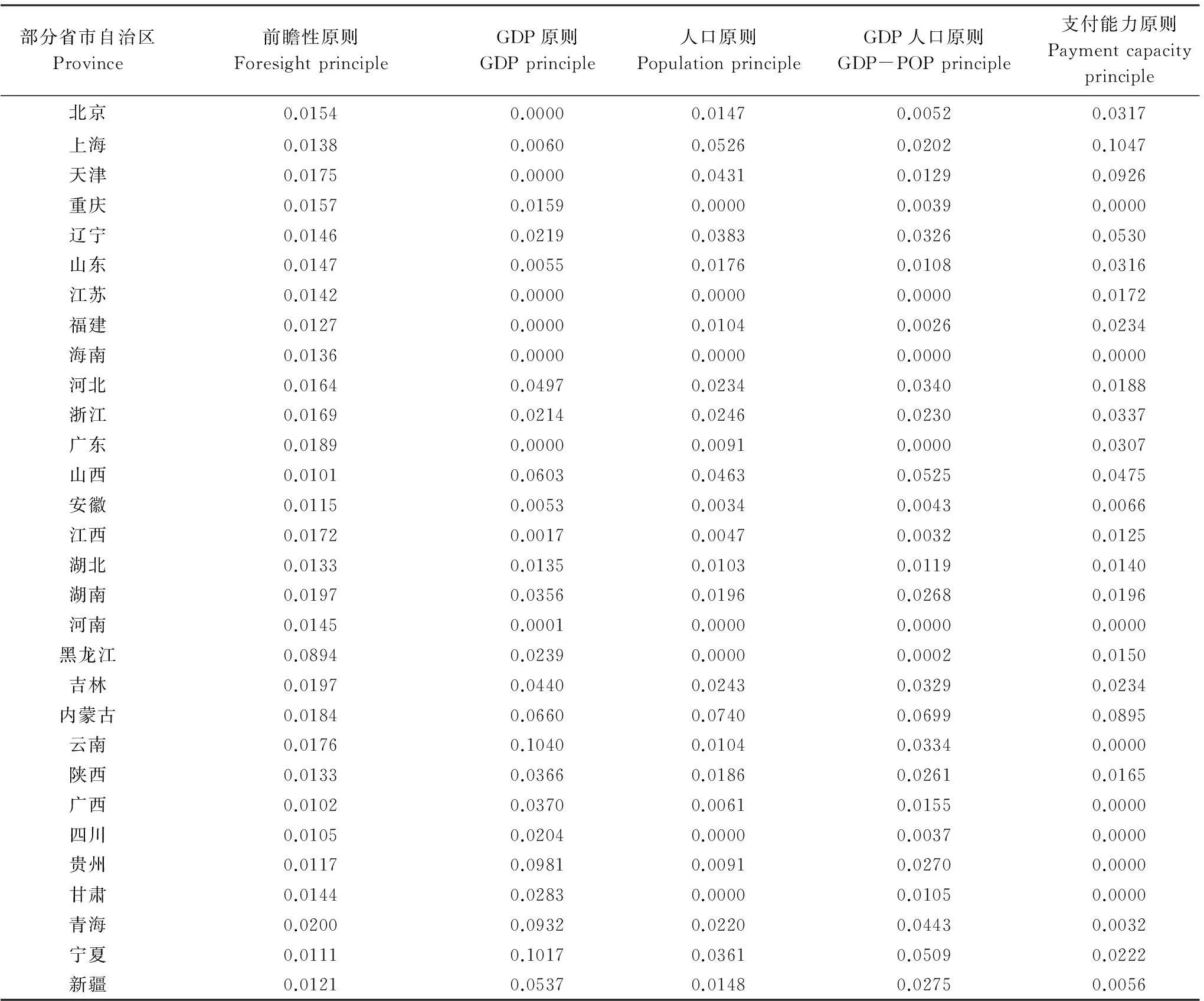
表1　部分省市自治區(區域)配額約束下的碳排放強度下降速率

此外，通過表1可以發現，在前瞻性原則下除青海省減排下降速率為0.02外， 各區域的減排下降速率處于0.01—0.02之間，說明前瞻性原則下各區域分配的配額量與累積碳排放需求量的差距都較小，在社會福利最大化的情況下，能以最小的減排控制率滿足累積碳排放量小于配額量這一約束目標。

3典型地區的碳減排控制

3.1減排控制率下的經濟增長路徑

根據前面得到的減排率，可以求出在社會福利最大化的情況下，根據各區域分配的配額獲得的經濟增長路徑。本文計算了5個分配原則下，全國30個區域的平穩增長率情況，限于篇幅，這里選取5個中國省區上海、山西，湖南、云南作為典型地區。選取的理由是上海是中國的制造業中心，山西為能源大省，能源碳排放居全國前列，湖南則是典型的中國中部正在快速工業化的地區，其人口，GDP，碳排放量都居全國中位，云南屬于人口較多，經濟總量較低的西南省份，新疆自治區則是人口和經濟都不高的西北省區。

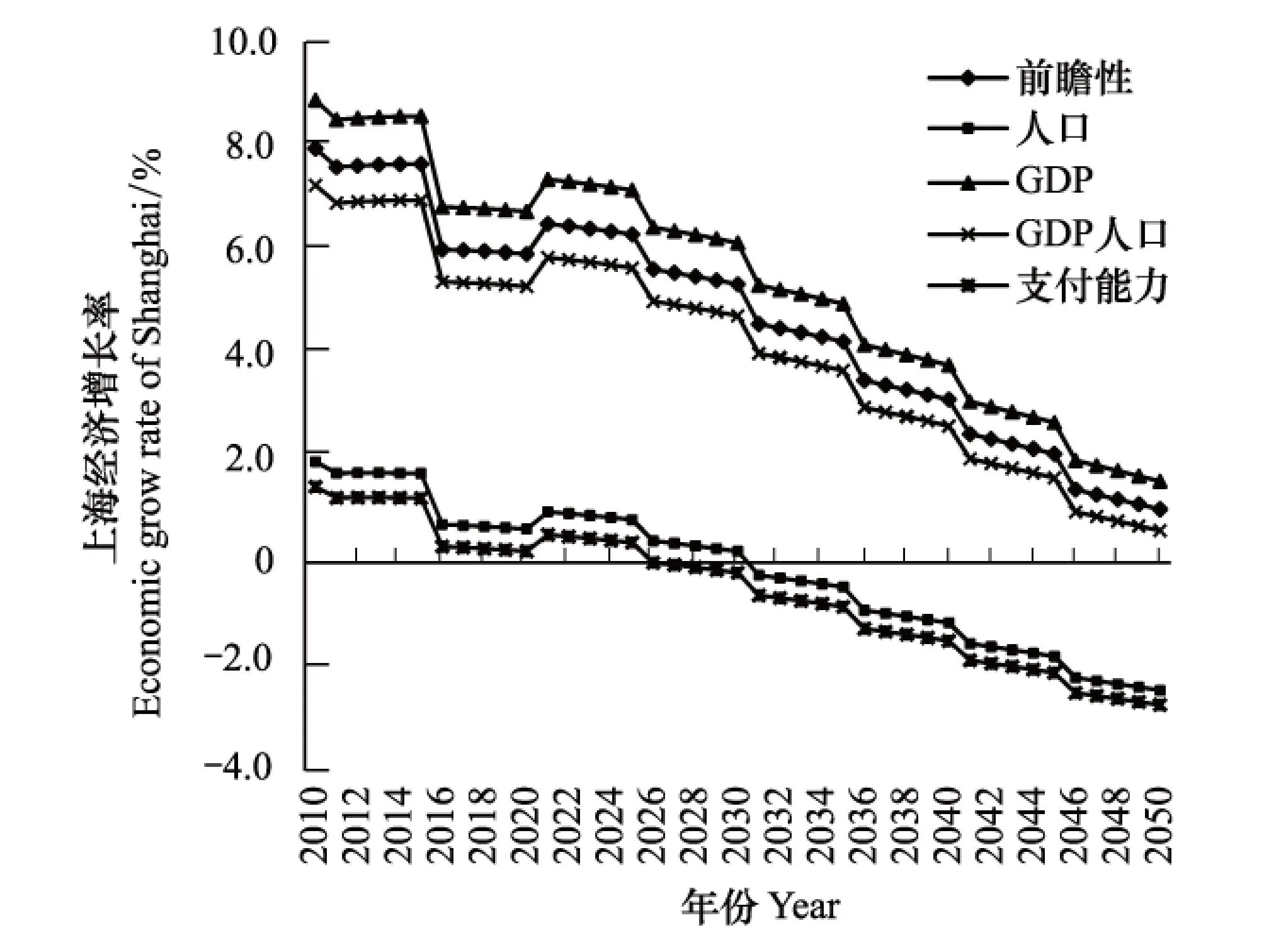
圖2　上海減排控制率下經濟增長率變化路徑　Fig. 2　The variation path of economic growth rate under the control of carbon emission reduction rate in Shanghai

模擬結果發現，中國在各種減排約束下各區域的經濟增長路徑呈階梯式下降，階梯是與勞動力參數設置遵循以五年為一個時間段的中短期規劃有關的，加之勞動參與率較小，出現整體下降趨勢。

圖2是上海市經濟增長率在減排控制率約束下的變化，各原則下的經濟增長率下降趨勢一致。再注意到表1，減排控制率越大，對經濟增長率的影響越大，其值與基年的值差距也越大。上海市在支付能力原則下，上海市的經濟增長率在初始年的經濟增長率就低于2%，隨著增長速度的下降，在后期甚至出現負增長。在這種情況下，上海只能有購買碳排放權來維持自己的增長。上海的增長率變化，表現中國東部將普遍遭遇的挑戰。

在圖3中，給出了中國能源基地山西省的經濟增長率變化，可以看出山西省在前瞻性原則下的經濟增長速率大于其他原則下的經濟增長率。由于山西省煤炭資源比較豐富，是我國產煤大省，在未來經濟發展過程中能源結構始終以碳排放量較多的煤為主，累積能源碳排放需求總量較大，使得山西省在前瞻性原則下分配的碳排放配額較多。因此，在較高的配額量約束下，滿足社會福利最大化目標所獲得的累積碳排放量也較多，導致山西省在前瞻性原則下的減排控制率較小，經濟增長率可以維持在較高水平。其他原則，在減排后期都出現負增長要求。

湖南省是中國中部工業化快速發展的地區，其GDP、人口在中國處于中間地位。圖4是湖南省在減排控制率約束下的經濟增長路徑的變化。從圖4可以看出湖南省各原則下的經濟增長曲線基本重疊，在不同減排控制率下各原則的經濟增長路徑保持一致，原因主要有兩方面，一方面說明湖南省5個原則下的減排控制率差距不大，另一方面說明湖南省的減排控制率對整個經濟生產過程的影響較小。由于減排控制率在生產過程中主要是通過對能源投入來影響經濟總量，再通過經濟總量的減少來降低碳排放量。而湖南省在配額約束下的能源強度下降速率較快，使得減排率對經濟的影響較小。比較圖3和圖4，發現，作為能源基地的山西，應該就可能滿足它的排放需求。相反，以湖南省為代表新興工業化的省份，由于其具有中間的人口數和產業規模，不同的配額原則影響其實并不大。

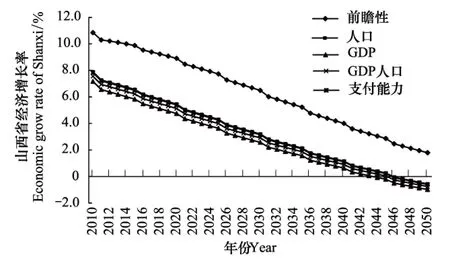
圖3　山西減排控制率下經濟增長路徑　Fig. 3　The variation path of economic growth rate under the control of carbon emission reduction rate in Shanxi

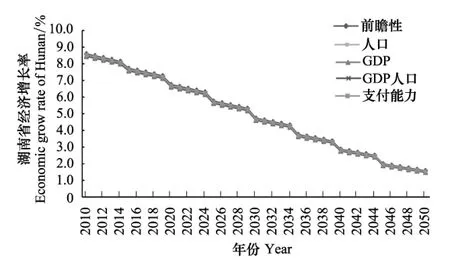
圖4　湖南減排控制率下經濟增長路徑　Fig. 4　The variation path of economic growth rate under the control of carbon emission reduction rate in Hunan

圖5，圖6分別為位于西南、西北的云南和新疆的經濟增長路徑。從圖5，圖6可以發現，云南省經濟增長率在支付能力原則下的經濟增長率最大，其次是人口原則，在GDP原則下的經濟增長率最小，這代表了大部分西部地區的經濟增長率的趨勢。落后的經濟以及較多的人口，使得西部地區在支付能力原則下和人口原則下分配的配額量較多。在配額目標較大的前提下，若要獲得較大的累積碳排放量，經濟總量勢必也較大，因此，在支付能力以及人口原則下的經濟增長率較大。新疆自治區在支付能力原則下的經濟增長率最大，在GDP原則和GDP人口原則下的經濟增長率較低并出現負值。這主要是由于在兩原則下的低碳配額量所導致，要實現在GDP原則下和GDP人口原則下的低配額量，須加大減排控制率，但此舉又將導致經濟呈負增長。可見，經濟落后地區并不適合按GDP原則和GDP人口原則分配配額量。

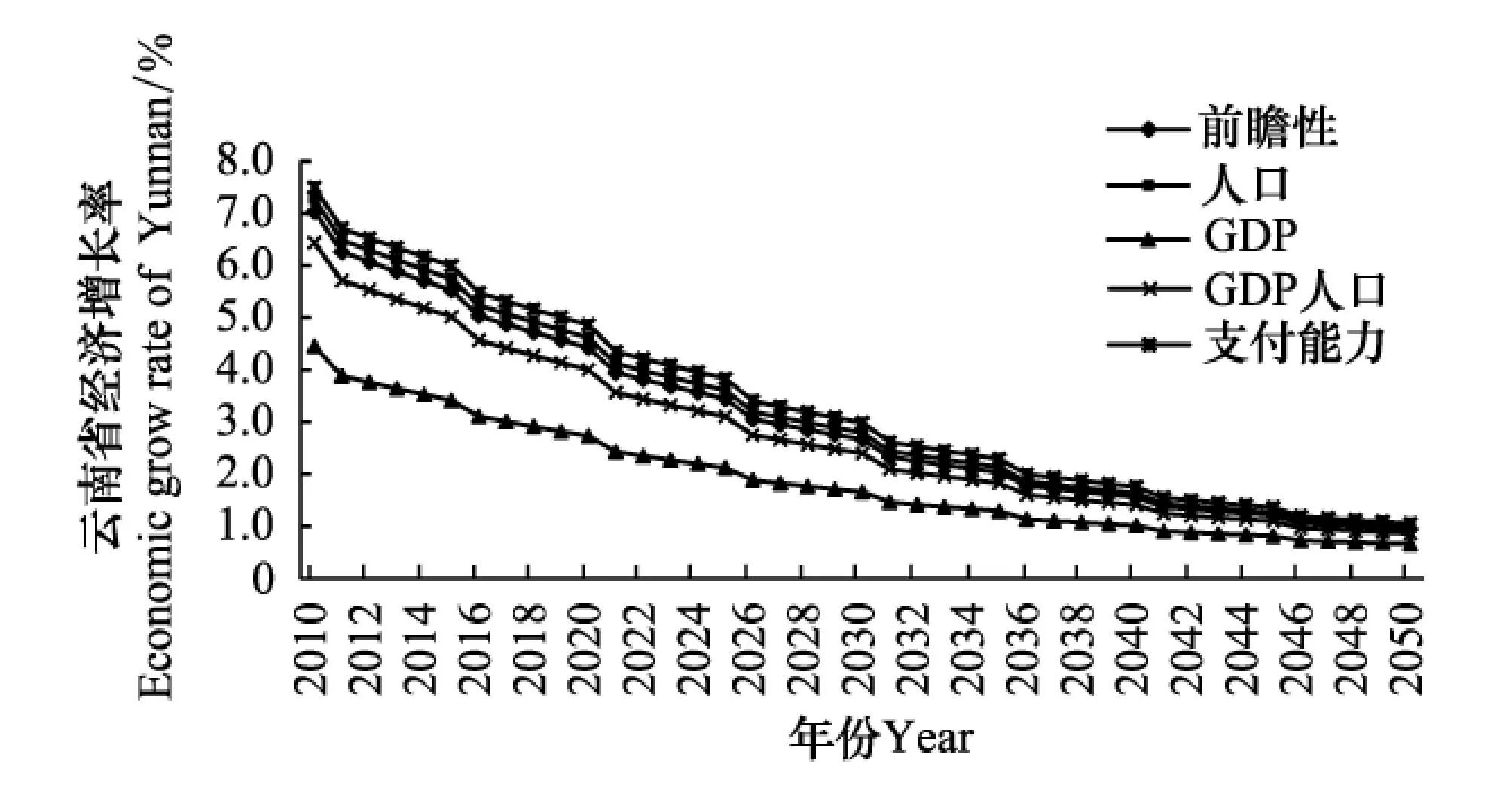
圖5　云南減排控制率下經濟增長路徑　Fig. 5　The variation path of economic growth rate under the control of carbon emission reduction rate in Yunnan

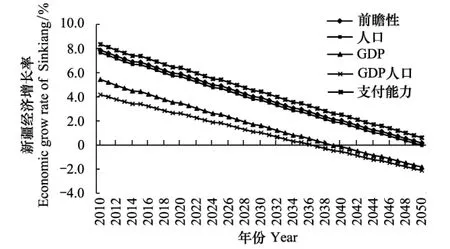
圖6　新疆減排控制率下經濟增長路徑　Fig. 6　The variation path of economic growth rate under the control of carbon emission reduction rate in Sinkiang

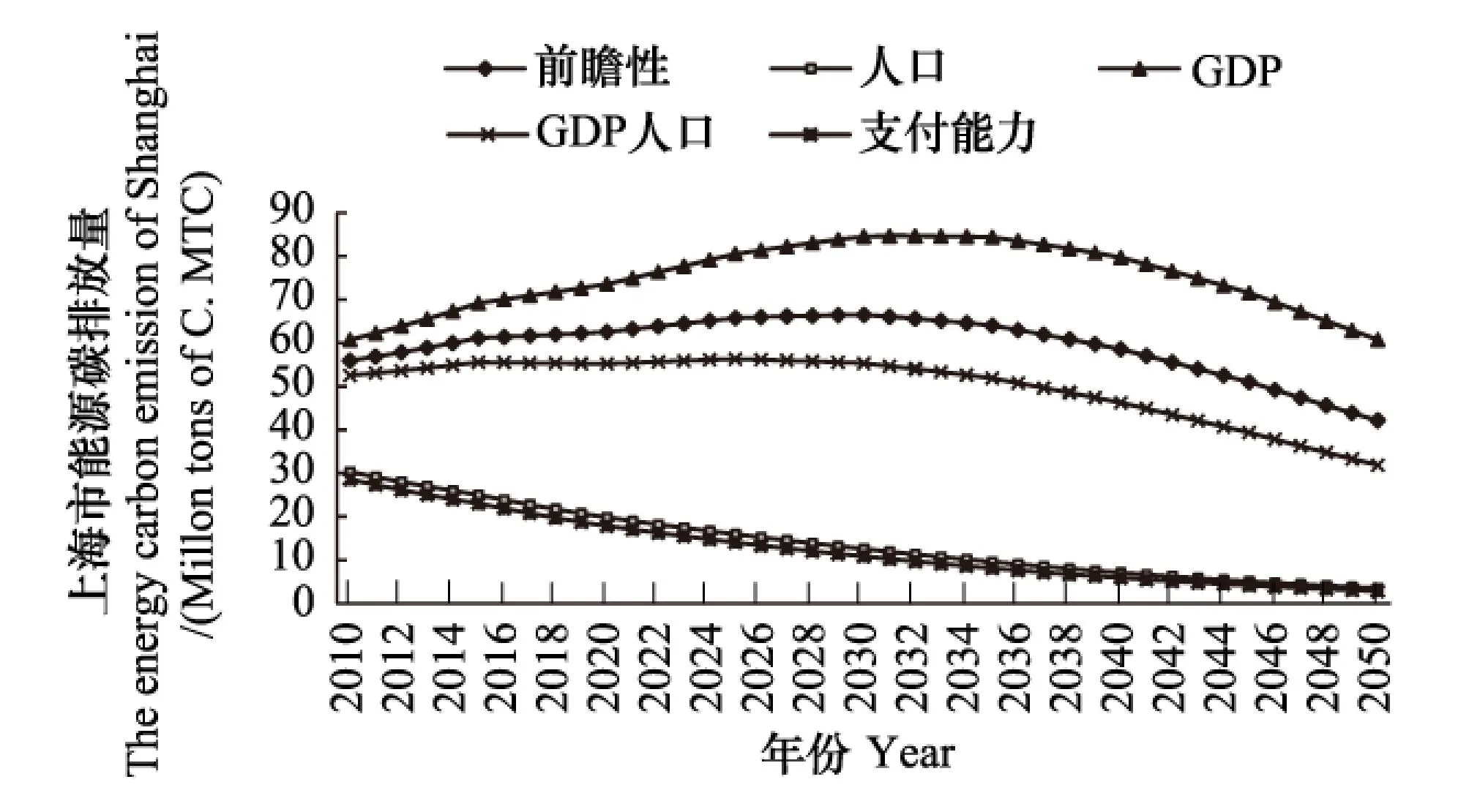
圖7　上海市減排控制率下能源碳排放路徑　Fig. 7　The variation path of energy carbon emission under the control of carbon emission reduction rate in Shanghai

比較各種減排配額給定的路線，可以發現保持5個區域在減排過程中的經濟增長始終存在正的增長率的只有按前瞻性原則實現碳配額分配。

3.2減排控制率下的能源碳排放路徑

在配額目標約束下獲得了未來各區域不同原則下的能源消費路徑的情況，乘以碳排放系數與各區域的能源結構可獲得各區域不同原則下的能源碳排放路徑。結果如圖7—圖10所示。

從圖7可以看出，上海在減排約束下各原則的能源碳排放整體呈下降趨勢。在GDP原則和前瞻性原則下的碳排放高峰年在2032年和2030年達到高峰后隨之下降，這反映了我國東部在正常情況下的碳排放將出現庫茨涅茲曲線。注意到Wang，Zhu，Peng得到在最優排放下中國碳排放的峰值出現在2032年[11]，而上海在減排情況下才能實現3032年高峰，可見由上海為代表的東部地區碳減排任務較重。

另一個代表性省份湖南的碳排放量變化如圖8所示，幾乎所有分配原則，都導致湖南省在2033年附近出現碳排放高峰，這與預期相一致。不過前瞻性原則下碳排放量相對較高。實際上這種情況在山西更為突出(圖9)。

從圖10和圖11可以看出，受能源消費量影響，云南和新疆的能源碳排放路徑較為相似，兩者都是在2036年左右到達碳排放量高峰后下降，并且各原則下的碳排放路徑排列順序也相近。兩省相對能源消費量，碳排放量變化不大，表明西部地區在未來發展過程中，主要是依靠減少能源投入使得經濟總量減少來達到碳排放量減少的目的，而非依靠提高技術進步降低能源強度來減少碳排放量。西部地區的碳減排，是中國碳減排的難點，特別是考慮到這些地方少數民族地區，經濟發展正屬于起步階段，如何控制他們的碳減排，需要進一步探索。

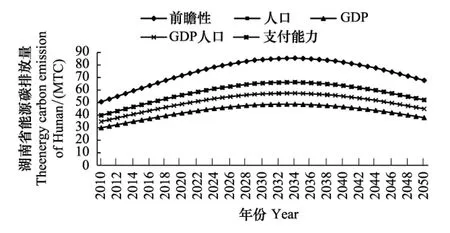
圖8　湖南省減排控制率下能源碳排放路徑　Fig. 8　The variation path of energy carbon emission under the control of carbon emission reduction rate in Hunan

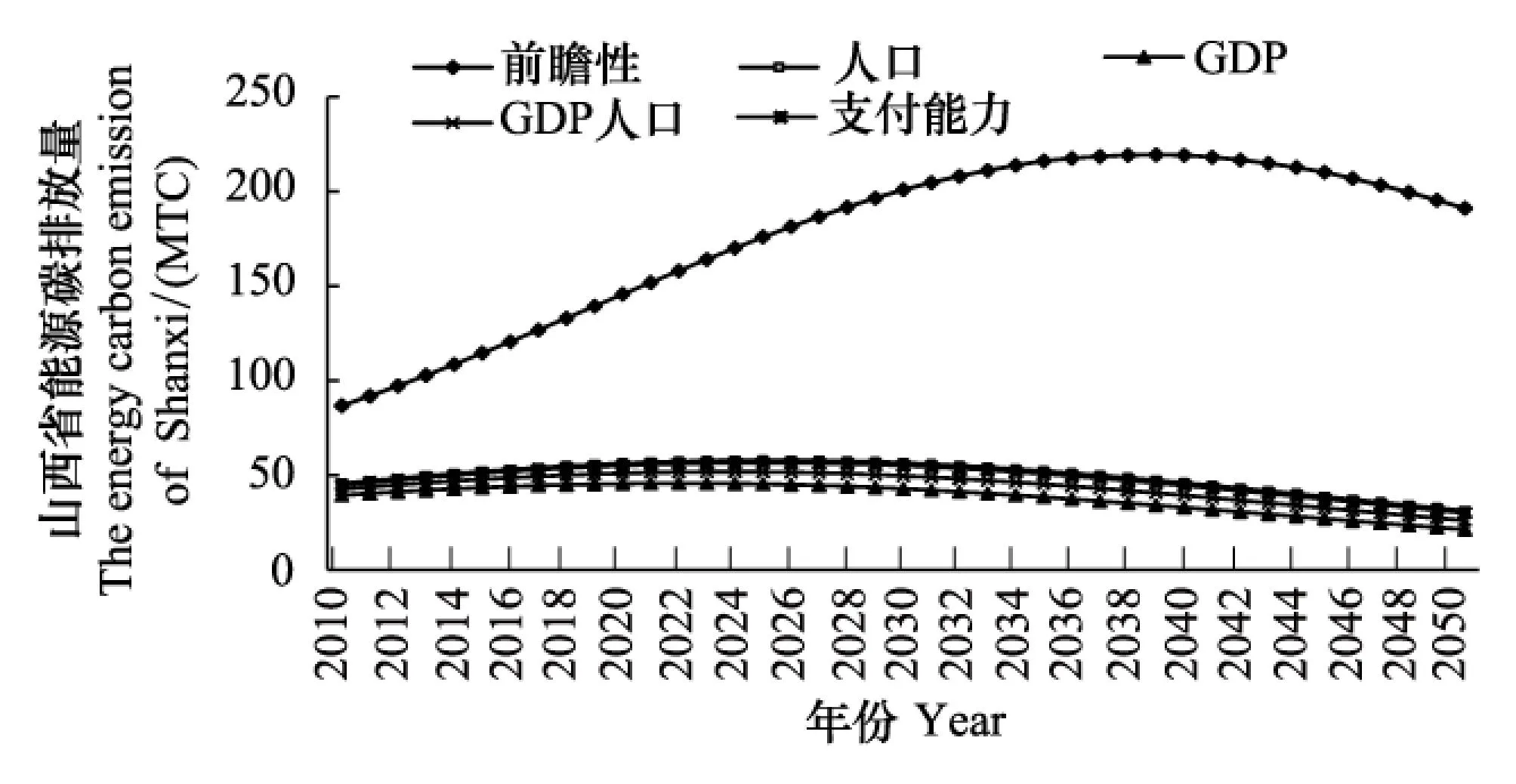
圖9　山西省減排控制率下能源碳排放路徑　Fig. 9　The variation path of energy carbon emission under the control of carbon emission reduction rate in Shanxi

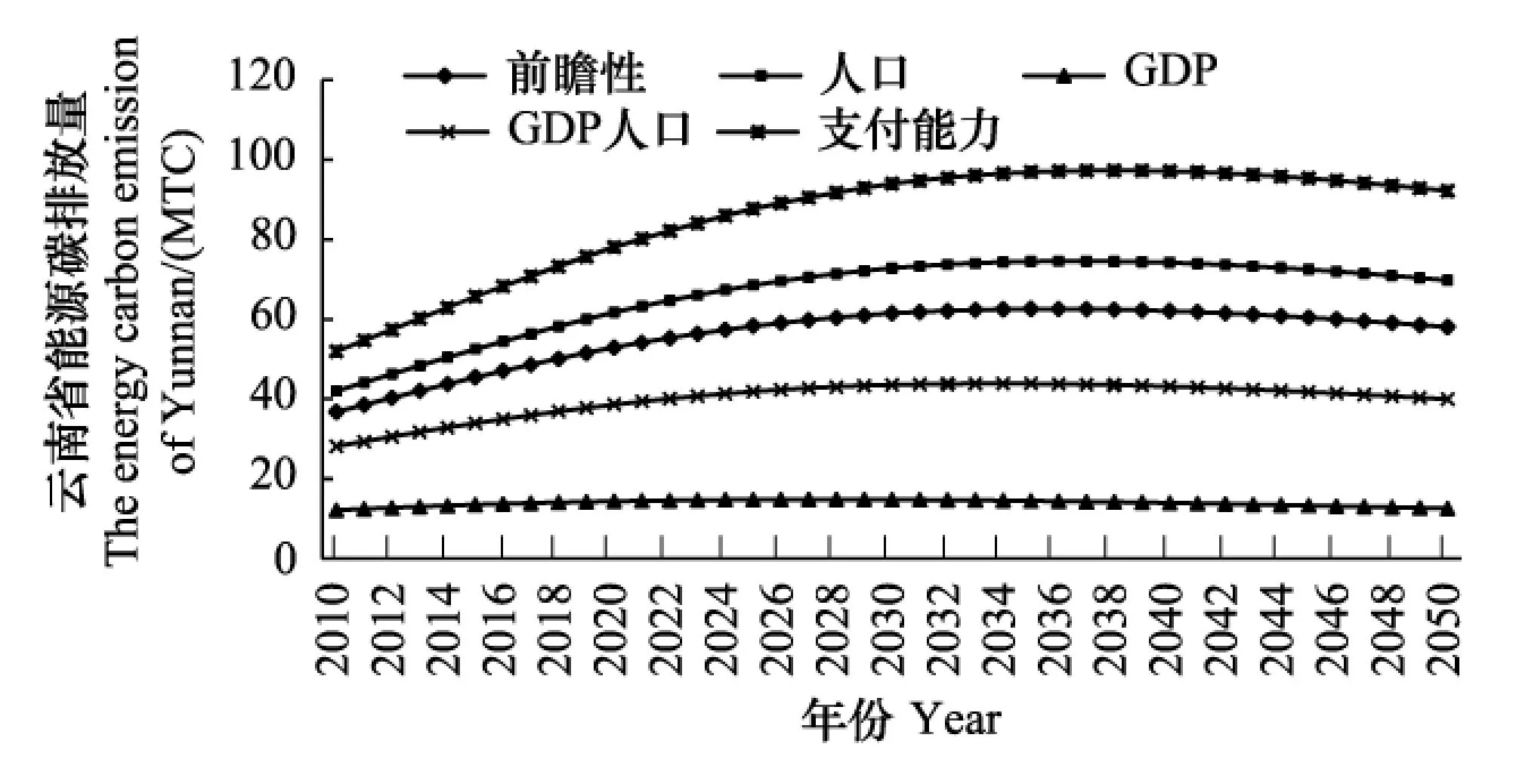
圖10　云南省減排控制率下能源碳排放路徑　Fig. 10　The variation path of energy carbon emission under the control of carbon emission reduction rate in Yunnan

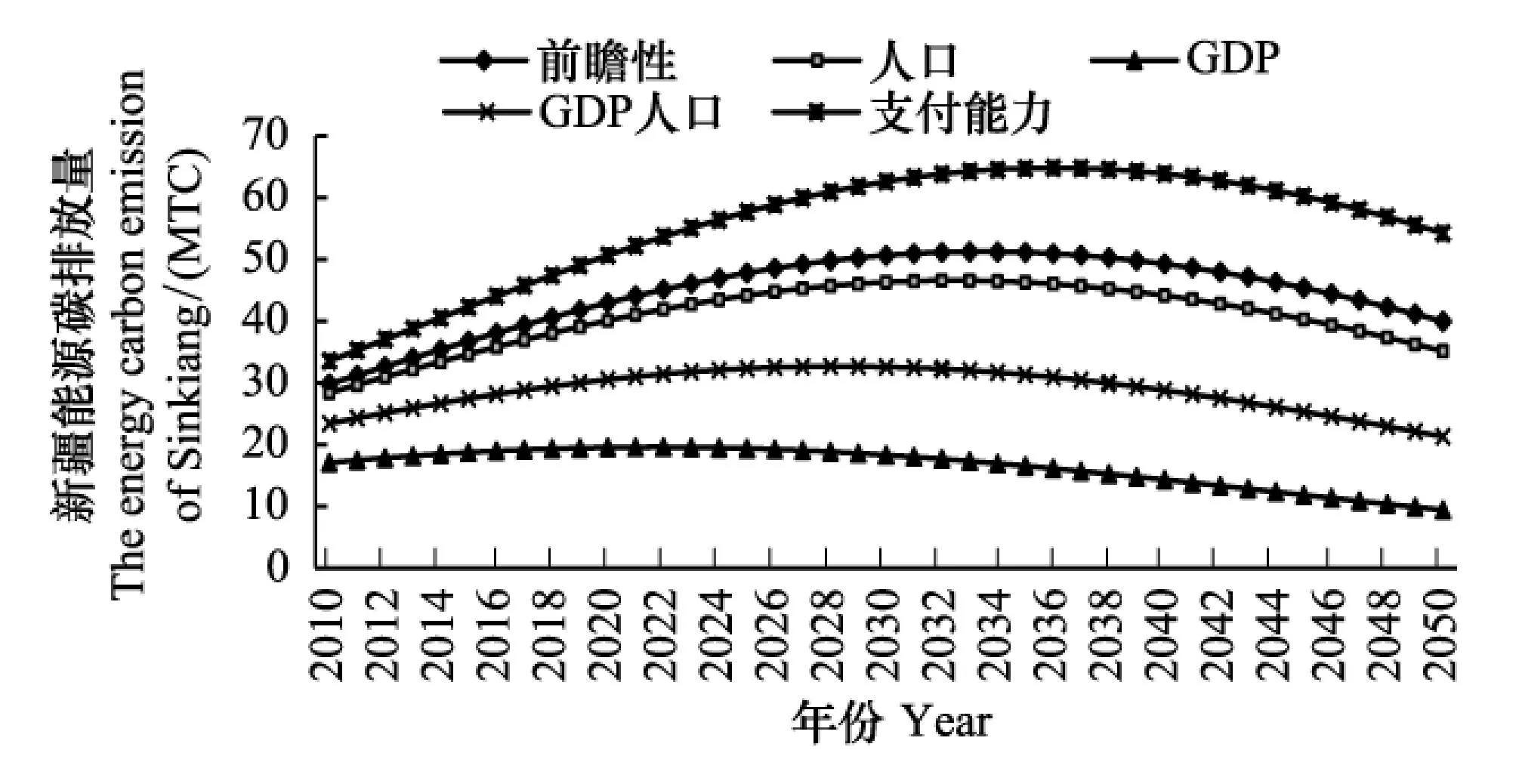
圖11　新疆自治區在不同排控制率下能源碳排放路徑　Fig. 11　The variation path of energy carbon emission under the control of carbon emission reduction rate in Sinkiang

4結論與討論

改進Nordhaus的減排模型，本文在碳排放動力學模型的基礎上，以追求社會福利最大化為目標，以累積碳排放量受五個原則分配的配額量為約束條件構建減排控制率模型，通過對該模型的求解，獲取各區域5個配額分配原則下的減排控制率。

通過減排控制率計算發現：

(1)各區域在不同原則下減排控制率不同，不同區域有適合其區域發展的分配原則。東部地區大部分省份在GDP原則分配的配額約束下減排控制率最小，西部地區大部分省份在支付能力原則下減排控制率最小，而中部地區則在人口原則下減排控制率較小的省份較多。

(2)各區域在前瞻性原則和GDP人口原則配額約束下的減排控制率差距較小，其中在前瞻性原則下差距最小，前瞻性原則下的減排速率差距最小，其他原則下的減排速率東西部差距都較大。所以，前瞻性原則是適合中國推進的碳減排配額方法。

此外，區域碳排放權分配和減排控制率的問題是個復雜的問題，對此還需要進一步研究的主要問題有：

(1)設置更多的情景模擬不同原則下中國大部分省市自治區的初始碳排放權分配。文章模擬的終端控制條件為社會福利最大化的同時，各省域累積碳排放量小于各原則下的配額量。受目標總配額的設定影響，這一約束條件使得全國有些省份自治區在完成這一目標時，可能存在經濟后期變為負增長的現象。可以設置不同的目標情景，對不同配額原則進行對比分析。

(2)進行不確定性分析。文章可進一步進行不確定性分析，以期使得結果更符合現實條件。

致謝：感謝華東師范大學地理信息科學教育部重點實驗室為本文提供了數據支持，感謝王錚課題組對本文細致的交流探討。感謝中國科學院科技政策與管理科學研究所吳靜副研究員對本文提供的幫助。

參考文獻(References):

[1]Zhu Y B, Wang Z. An optimal balanced economic growth and abatement pathway for China under the carbon emissions budget. Computational Economics, 2014, 44(2): 253- 268.

[2]Nordhaus W D. Managing the Global Commons. Cambridge: The MIT Press, 1994.

[3]Nordhaus W D, Pop D. What is the value of scientific knowledge? An application to global warming using the PRICE model. Energy Journal, 1997, 18: 1- 45.

[4]Pizer W A. The optimal choice of climate change policy in the presence of uncertainty. Resource and Energy Economics, 1999, 21(3- 4): 255- 287.

[5]崔麗麗, 王錚, 劉揚. 中國經濟受 CO2減排率影響的不確定性 CGE 模擬分析. 安全與環境學報, 2002, 2(1): 39- 43.

[6]沈子榮. 中國單位GDP碳減排率的計算與比較. 國際經濟合作, 2012, (4): 70- 73.

[7]丁仲禮, 段曉男, 葛全勝, 張志強. 2050年大氣CO2濃度控制: 各國排放權計算. 中國科學, 2009, 39(8): 1009- 1027.

[8]姜克雋, 胡秀蓮, 劉強, 莊幸. 2050低碳經濟情景預測. 環境保護, 2009, (24): 28- 30.

[9]付雪, 王桂新, 彭新哲. 哥本哈根會議目標下中國行業實際減排潛力研究——基于2007年中國能源—碳排放—經濟投入產出表的最優化模型. 復旦學報: 社會科學版, 2012, (4): 114- 124.

[10]林伯強, 孫傳旺. 如何在保障中國經濟增長前提下完成碳減排目標. 中國社會科學, 2011, (1): 64- 76.

[11]Wang Z, Zhu Y B, Peng Y M. Carbon emissions trends with optimal balanced economic growth of China and the USA and some abatement options for China. Journal of Geographical Sciences, 2013, 23(6): 991- 1004.

[12]Nordhaus W D. Optimal greenhouse-gas reductions and tax policy in the “DICE” model. American Economic Review, 1992, 83(2):313- 317.

[13]Barro，R J.,Shalaimatin,X 2002，EconomicGrowth，The MIT Press， Cambridge， Massachusetts.

[14]吳靜, 馬曉哲, 王錚. 我國省市自治區碳排放權配額研究. 第四紀研究, 2010, 30(3): 481- 488.

The optimal control rate of regional emission reduction targets under the constraint of quotas

LIU Xiao1,2, WANG Zheng2,3,*, DENG Jixiang2,4

1Hunanacademicofsocialscience,Changsha410003,China2KeyLaboratoryofGeographicalInformationScience,MinistryofStateEducationofChina,EastChinaNormalUniversity,Shanghai200062,China3InstituteofPolicyandManagement,ChineseAcademyofSciences,Beijing100190,China4ChangshaUniversity,Changsha410006,China

Abstract：Allocation of carbon dioxide emission rights is one of the effective ways to reduce carbon dioxide emissions. Therefore, an annual reduction rate needs to be determined to achieve this goal gradually. Given the negative effect of the emission reduction on economy, it is necessary to perform the emission reduction under the conditions of optimal and balanced economic growth, without causing an economic crisis. Hence, an optimal and balanced economic growth pathway is taken into account during calculations of the optimal control rate of carbon dioxide emission reduction. In this study, consequently, we try to determine the optimal control rate of carbon dioxide emission reduction that ensures balanced economic growth, with the constraint of the objective of a certain regional carbon dioxide emission quota. First, we present a calculation flow chart showing how to achieve the optimal control rate of carbon dioxide emission reduction. On the basis of the flow chart, we describe an algorithm aimed at determining the optimal control rate of carbon dioxide emission reduction and use it to calculate such a rate for each province given their carbon dioxide emission quota determined by means of the allocation principles forward-looking, population, GDP, GDP-population, and ability-to-pay. A higher control rate of carbon dioxide emission reduction means more efforts are needed to reduce the carbon dioxide emission. Furthermore, in this study, we selected five provinces and autonomous regions of China (Shanghai, Shanxi, Hunan, Yunnan, and Xinjiang) as research cases, analyzed the path of economic growth and energy-induced carbon dioxide emission with the objective of welfare maximization and the constraint of carbon dioxide emission quota for the participating regions. The simulation shows that the growth rate of the economy drops gradually under the constraints of carbon dioxide emission reduction in all regions. For instance, the economic growth rate of Shanghai is lower than that in other eastern provinces and even negative along with a decline of the economic growth rate at later development stages (with the principle of ability-to-pay). Shanghai has to purchase carbon dioxide emission quota rights to keep the positive economic growth rate in the future. Shanxi attains a lower emission reduction rate by means of the forward-looking principle, which maintains Shanxi′s economic growth rate at a relatively high level. Hunan stays on a similar path of economic growth and an emission reduction rate with various allocation principles. Therefore, the principle of emission right allocation has a smaller effect on the economy and on the reduction rate. Yunnan shows a higher economic growth rate with the principle of ability-to-pay, followed by the scenario involving the population principle. With the principle of GDP, the economic growth rate is the lowest. Similarly, Xinjiang achieves the highest economic growth rate with the principle of ability-to-pay, and lowest or even negative growth rate with the GDP or GDP-population principle. The carbon dioxide emission will first increase and then decrease, and the peak years of carbon dioxide emission are 2032 for Shanghai, 2033 for Hunan, 2036 for both Yunnan and Xinjiang, and 2039 for Shanxi province. Hence, more efforts are needed if these provinces want to achieve their carbon dioxide emission peak before 2030. Finally, we found that eastern provinces require the minimum reduction rate when using the GDP principle; western provinces by means of the ability-to-pay principle; and central provinces by means of the population principle. Among all the allocation principles, the forward-looking principle is suitable for China to allocate the carbon dioxide emission rights from the standpoint of carbon dioxide control and regional disparities in growth rate.

Key Words:carbon emissions reduction; control rate; quota; climate change

基金項目:國家重大研究計劃(973)項目(2012CB955800);國家社會科學基金(14CJY032);中國科學院戰略性先導科技專項(XDA05150900)

收稿日期:2014- 07- 25; 網絡出版日期:2015- 07- 22

DOI:10.5846/stxb201407251506

*通訊作者Corresponding author.E-mail: wangzheng@casipm.ac.cn

劉曉, 王錚, 鄧吉祥.配額目標約束下區域減排的最優控制率.生態學報,2016,36(5):1380- 1390.

Liu X, Wang Z, Deng J X.The optimal control rate of regional emission reduction targets under the constraint of quotas.Acta Ecologica Sinica,2016,36(5):1380- 1390.