非線性耦合Harry-Dym方程的對稱約化

胡　瀟,　胡恒春

(上海理工大學 理學院,上海　200093)

?

非線性耦合Harry-Dym方程的對稱約化

胡瀟,胡恒春

(上海理工大學 理學院,上海200093)

摘要:借助符號計算軟件Maple將Clarkson-Kruskal直接法應用于非線性耦合Harry-Dym方程中,運用相應規則得到對稱變換并求得非線性耦合Harry-Dym方程的相似變量和相似解.通過選取不同的特殊常數得到非線性耦合Harry-Dym方程兩種常微分形式的對稱約化方程.利用約化方程構造了非線性耦合Harry-Dym方程可能的新嚴格解.

關鍵詞:對稱約化; Clarkson-Kruskal直接法; 非線性耦合Harry-Dym方程

1問題的提出

眾所周知,孤立子理論是非線性科學的重要組成部分.一般來說,孤立子理論的研究對象大多數是非線性系統,這些非線性系統可以描述流體力學、等離子物理學、非線性光學及環境科學等領域出現的某些非線性現象.因此,對非線性系統的精確求解問題在理論上和應用上都具有重要的研究意義[1-2].近年來,經過數學家和理論物理學家的不懈努力,提出了許多行之有效的構造非線性系統精確解的方法,如反散射方法、貝克隆變換法、tanh-coth展開方法、廣田雙線性法、分離變量法、達布變換法及李群方法等.

由于非線性系統不滿足解的線性疊加原理,人們很難求出它們所有的精確解．因此,需要尋求一些簡單的方法來簡化復雜的非線性系統,使之轉化為低維的偏微分方程或常微分方程,通過求解低維的偏微分方程或常微分方程,進而得出原來非線性系統的精確解．

本文主要研究非線性耦合Harry-Dym方程,簡稱cHD方程,其形式為

(1)

式中,p為常數.

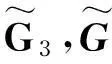
2方法簡介

人們對偏微分方程的對稱性研究主要包括尋找方程所允許的對稱群、對稱約化和群不變解[10].尋找偏微分方程對稱約化的方法有很多,其中主要有以下3種方法:a.Lie的經典無窮小變換法[11];b.Bluman和Cole的非經典無窮小變換法[12];c.Clarkson和Kruskal提出的CK直接法[13-14].

1989年Clarkson和Kruskal首次提出的CK直接法是用來推導非線性偏微分方程的相似約化的直接方法,這是一種不涉及群論的直接約化方法.Clarkson和Kruskal用這種方法最先求解的是Boussinesq方程[13],得出很多不同于用經典無窮小變換和非經典無窮小變換方法求出的相似解.1990年Lou[14]完善了這種方法,并且推廣到(2+1)維KP方程中,獲得了一些相似解.之后，這種方法被推廣應用于方程組等其他一大批非線性方程[15-16].2000年Lou提出了條件約化的概念[17],并用直接約化法的思想獲得了(2+1)維KdV方程的6種新的條件相似約化,該條件相似約化不能由現有非古典理論推得.

對于非線性偏微分方程

(2)

直接尋找偏微分方程如下形式的相似解：

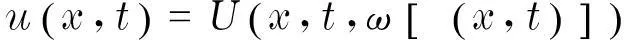
(3)

式中,函數U,ξ待定.

這是最一般的相似約化的形式.將式(3)代入式(2)中,要求結果是關于ω的低維偏微分方程或常微分方程,附加條件與U,ξ及它們的導數有關,而后能夠進一步解出U,ξ的具體形式.

對于一般低維對稱性約化,可以選取

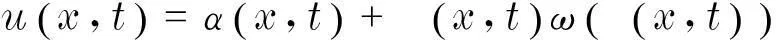
(4)

以耦合非線性Harry-Dym 方程為例,將CK直接法的步驟歸納如下：

a. 設方程(1)具有對稱變換

(5)

式中,α1,α2,β1,β2,ξ是關于x,t的待定函數且G,Q是關于ξ的偏微分方程;

b. 將對稱變換方程(5)代入方程(1),整理化簡找出規范系數，通常以最高階導數的系數作為規范系數;

c. 令各項導數的系數與規范系數分別成比例,應用相應規則求出待定函數;

d. 根據步驟c求出的各個變量得到對稱變換,代入原方程(1),確定約化方程.

在步驟c中,提到的相應的規則為:

規則1若α1(x,t)滿足形式α1=α10(x,t)+β1(x,t)Ω(ξ(x,t)),則可取Ω(ξ(x,t))=0.

規則2若α2(x,t)滿足形式α2=α20(x,t)+β2(x,t)Ω(ξ(x,t)),則可取Ω(ξ(x,t))=0.

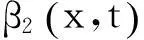
規則5如果ξ(x,t)由Ω(ξ)=ξ0(x,t)定義得出,其中,Ω(ξ)是任意可逆函數,則可取Ω(ξ)=ξ0.

3非線性耦合Harry-Dym方程的相似約化

將方程(5)代入方程(1)中,得到

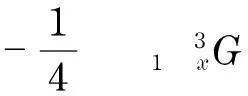
(6)

(7)

要求方程(6)和方程(7)僅僅是有關G,Q以及它們各階導數的常微分方程.在方程(6)中用G?的系數作為歸一化系數,能夠得到

式中,Γ1,Γ2,…,Γ8都是僅僅與ξ有關的待定函數.

在方程(7)中選擇Q′G作為歸一化系數,可得

式中,Ω1,Ω2,…,Ω7都是僅僅與ξ有關的待定函數.

現考慮ξx的兩種情況.

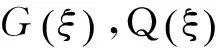
b. 當ξx≠0時,在方程(6)中由G?和G′G前面的系數可得

(8)

對方程(8)利用上述規則3,可知

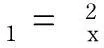
得到

利用上述規則5,可知

因此

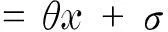
(9)

很顯然

(10)

將β1=θ2,ξ=θx+σ代入方程

并利用上述規則4,可得

(11)

繼續利用上述規則1和規則2,很容易得到

(12)

將式(9)～(12)代入方程

可得

(13)

因為,ξ=θx+σ,方程(13)左邊是關于x的線性函數,因此,Γ3具有如下形式:

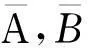
因此,有

通過比較有關x的系數,可知

(14)

(15)

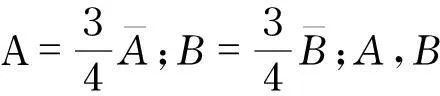
因此,非線性耦合Harry-Dym方程的對稱約化為

(16)

將方程(14)～(16)代入方程(1)中,可得

(17)

考慮方程(17)的不同常數選取.

a. 當A=0時,有

式中,c1,c2是任意常數.

與之對應的對稱約化為

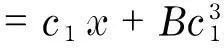
對應方程(1)的約化方程為

(18)

b. 當A≠0時,方程(14)和方程(15)的解為

式中,c1,c2是任意常數.

與之對應的對稱約化為

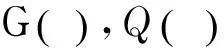
不同的約化方程(17)和方程(18),它們的通解形式只能用復雜隱函數形式來表示,這里省略其具體表達式.

4結論

利用CK直接法求得非線性耦合Harry-Dym方程的對稱約化,得到了非線性耦合Harry-Dym方程的約化后的常微分方程組,進而建立了非線性耦合Harry-Dym方程與這些常微分方程組的關系.非線性耦合Harry-Dym方程的其他可積性質,如Painlevé可積性、共性Tanh可積性等[18-19],將是今后研究工作的一個重要內容.

參考文獻:

[1]谷超豪.孤立子理論與應用[M].杭州:浙江科學技術出版社,1990.

[2]李翊神.孤子與可積系統[M].上海:上海科技教育出版社,1999.

[3]Xu T X,Mu W H.Finite-dimensional completely integrable systems associated with the Harry-Dym and the coupled Harry-Dym hierarchies[J].Physics Letters A,1990,147(2/3):125-129.

[4]曹策問,耿獻國.系統與耦合Harry-Dym方程解的對合表示[J].數學學報,1992,35(3):314-322.

[5]Chen J B,Geng X G.A new Neumann type integrable system related to the coupled Harry-Dym hierarchy[J].Physics Letters A,2005,340(1/2/3/4):181-187.

[6]Chen J B,Geng X G.On the linearization of the coupled Harry-Dym soliton hierarchy[J].Chinese Physics B,2006,15(7):1407-1413.

[7]Yang H W,Dong H H.Multi-component Harry-Dym hierarchy and its integrable couplings as well as their Hamiltonian structures[J].Chinese Physics B,2009,18(3):845-849.

[8]Marciniak K,Blaszak M.Construction of coupled Harry-Dym hierarchy and its solutions from St?ckel systems[J].Nonlinear Analysis:Theory,Methods & Applications,2010,73(9):3004-3017.

[9]張穎,李吉娜,張江紅.耦合的Harry-Dym方程的對稱約化[J].西北大學學報,2011,41(6):960-963.

[10]Lie S.Uber die integration durch bestimmte integrale von einer classe linearer partieller differential-gleichungen[J].Archive for Mathematics,1881,6(3):328-368.

[11]Bluman G W,Kumei S.Symmetries and differential equations[M].New York:Springer-Verlag,1989.

[12]Olver P J.Applications of lie groups to differential equations[M].2nd ed.New York:Springer-Verlag,1993.

[13]Clarkson P A,Kruskal M D.New similarity reductions of the Boussinesq equation[J].Journal of Mathematical Physics,1989,30(10):2201-2213.

[14]Lou S Y,A note on the new similarity reductions of the Boussinesq equation[J].Physics Letters A,1990,151(3/4):133-135.

[15]Clarkson P A,Winternitz P.Nonclassical symmetry reductions for the Kadomtsev-Petviashvili equation[J].Physica D:Nonlinear Phenomena,1991,49(3):257-272.

[16]Lou S Y.Generalized Boussinesq equation and KdV equation-Painlevé properties,B?cklund transformations and Lax pairs[J].Science in China Series A:Mathematics,1991,34(9):1098-1108.

[17]Lou S Y,Tang X Y,Lin J.Similarity and conditional similarity reductions of a (2+1)-dimensional KdV equation via a direct method[J].Journal of Mathematical Physics,2000,41(12):8286-9303.

[18]裴勝兵,張衛國,李想.色散項系數為負的mKdV-Burgers方程的有界行波解[J].上海理工大學學報,2014,36(3):205-216.

[19]劉磊,胡恒春,高海潮.Jaulent-Miodek方程的Painlevé可積性及精確解[J]. 上海理工大學學報,2014,36(3):217-222.

(編輯:石瑛)

Symmetry Reduction for the Nonlinear Coupled Harry-Dym Equation

HU Xiao,HU Hengchun

(College of Science,University of Shanghai for Science and Technology,Shanghai 200093,China)

Abstract:With the help of symbolic computation software Maple,the Clarkson-Kruskal direct method was developed for the nonlinear coupled Harry-Dym equation,the similarity variables and similarity solutions of the nonlinear coupled Harry-Dym equation were obtained by the symmetry transformation.Two forms of symmetric reduced equation were obtained by selecting different special contants.The exact solutions of the reduction equation were also constructed directly.

Keywords:symmetry reduction; Clarkson-Kruskal direct method; nonlinear coupled Harry-Dym equation

中圖分類號:O 175

文獻標志碼:A

通信作者:胡恒春(1976-),女,副教授.研究方向:孤立子理論與可積系統.E-mail:hhengchun@163.com

基金項目:上海市自然科學基金資助項目(10ZR1420800);上海市重點學科建設項目(XTKX2012);國家自然科學基金資助項目(11071164,11201302)

收稿日期:2014-10-24

DOI:10.13255/j.cnki.jusst.2016.01.002

文章編號:1007-6735(2016)01-0008-05

第一作者: 胡瀟(1991-),女,碩士研究生.研究方向:孤立子理論與可積系統.E-mail:huxiaomath@163.com