彈體侵徹混凝土的臨界跳彈*

段 建,王可慧,周 剛,薛斌杰,初 哲,李 明,戴湘暉,耿寶剛

(西北核技術研究所，陜西 西安 710024)

彈體侵徹混凝土的臨界跳彈*

段 建,王可慧,周 剛,薛斌杰,初 哲,李 明,戴湘暉,耿寶剛

(西北核技術研究所，陜西 西安 710024)

為了保證鉆地戰斗部打擊防護層目標時不發生跳彈，需要對彈體侵徹目標的臨界跳彈角度進行分析和估算。開展了一定大長徑比彈體斜侵徹混凝土的跳彈實驗，分析了在250～430 m/s速度下彈體侵徹30和60 MPa鋼筋混凝土的臨界跳彈角度，給出了彈體臨界跳彈角度包絡線。當靶板強度相同時，隨著侵徹速度的增加，彈體的臨界跳彈傾角增大，增大的趨勢逐漸變緩；在相同侵徹速度下，隨著靶板強度的增加，彈體的臨界跳彈傾角減小；經驗公式分析得到的彈體臨界跳彈傾角偏低于實驗，但偏差基本在3°以內。

爆炸力學；跳彈性能；侵徹戰斗部；混凝土；臨界跳彈角度

鉆地戰斗部對地下深埋加固目標的有效打擊模式是貫穿防護層介質、侵入目標結構內部爆炸，依靠爆炸產生的沖擊波和破片等對目標內部的設施和人員進行破壞和毀傷[1]。然而，在實際作戰過程中，由于載體作用方式、目標表層特性、彈體的氣動性能以及末端制導等因素的影響，戰斗部攻擊目標時將會有一定的傾角和攻角[2-3]。當戰斗部的傾角或攻角大于某一臨界角度時，將產生跳彈[4]。

跳彈是彈體在斜侵徹過程中產生的一種特殊現象，就是彈丸侵入或者碰擊目標介質后、又從介質表面跳出來并繼續在空中運動的現象。彈體一旦跳彈，就失去了對目標的侵徹功能，戰斗部侵入不到目標內部，就不能對目標內的設施及人員形成有效打擊。因此，為保證戰斗部有效侵徹目標，需要對戰斗部侵徹目標的臨界跳彈角度進行分析和估算，確保戰斗部侵徹目標時的角度控制在臨界跳彈角度范圍以內。一般情況下，彈體的攻角能夠控制，而傾角的影響因素多、變化范圍大。因此，本文中僅對傾角下的彈體跳彈性能開展研究。

對彈體在傾角下的跳彈研究，相關文獻報道主要集中在跳彈現象和數值模擬方面[4-6]，而在實驗方面的研究較少。本文中，開展一定大長徑比彈體(長徑比L/d=8.32)在250～430 m/s速度下侵徹30和60 MPa鋼筋混凝土的跳彈實驗，分析彈體侵徹鋼筋混凝土的臨界跳彈角度，結合經驗公式分析結果，給出彈體臨界跳彈角度包絡線，擬為進行戰斗部有效作戰提供技術指導和依據。

1 實 驗

1.1 方案

在130 mm輕氣炮上，進行不同傾角下彈體侵徹混凝土靶板實驗，研究彈體不同速度下侵徹混凝土靶板的跳彈情況，分析彈體臨界跳彈角度。實驗原理如圖1所示。彈托起定心、閉氣的作用。高壓氣體釋放后在膛內形成高壓，推動彈托和彈體沿炮膛加速運動，使得彈體以一定的速度撞擊斜置的混凝土靶板。調整混凝土靶板的傾斜角度，可以設計不同傾角的彈體撞靶實驗，研究彈體產生跳彈的臨界角度。

對彈體進行彈托脫殼設計，實現了彈體撞擊靶板前的彈、托分離，消除了彈托對彈體撞靶瞬間受力和姿態的影響。脫殼原理如圖2所示。彈和彈托向前高速飛行，當彈托接觸脫殼器時，脆性材料作為彈托，撞擊瞬間發生碎裂，由于彈托結構對稱且材料均勻，近似認為破碎沿彈軸對稱，可以忽略它對彈體姿態的影響，碎塊在氣動力的作用下遠離彈體。這樣，彈體與彈托分離，彈體將在姿態幾乎不受干擾的情況下飛行并撞靶。

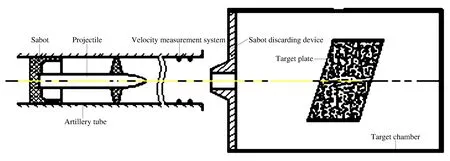
圖1 傾角侵徹實驗原理示意圖Fig.1 Schematics of penetrator impacting targets with oblique angle

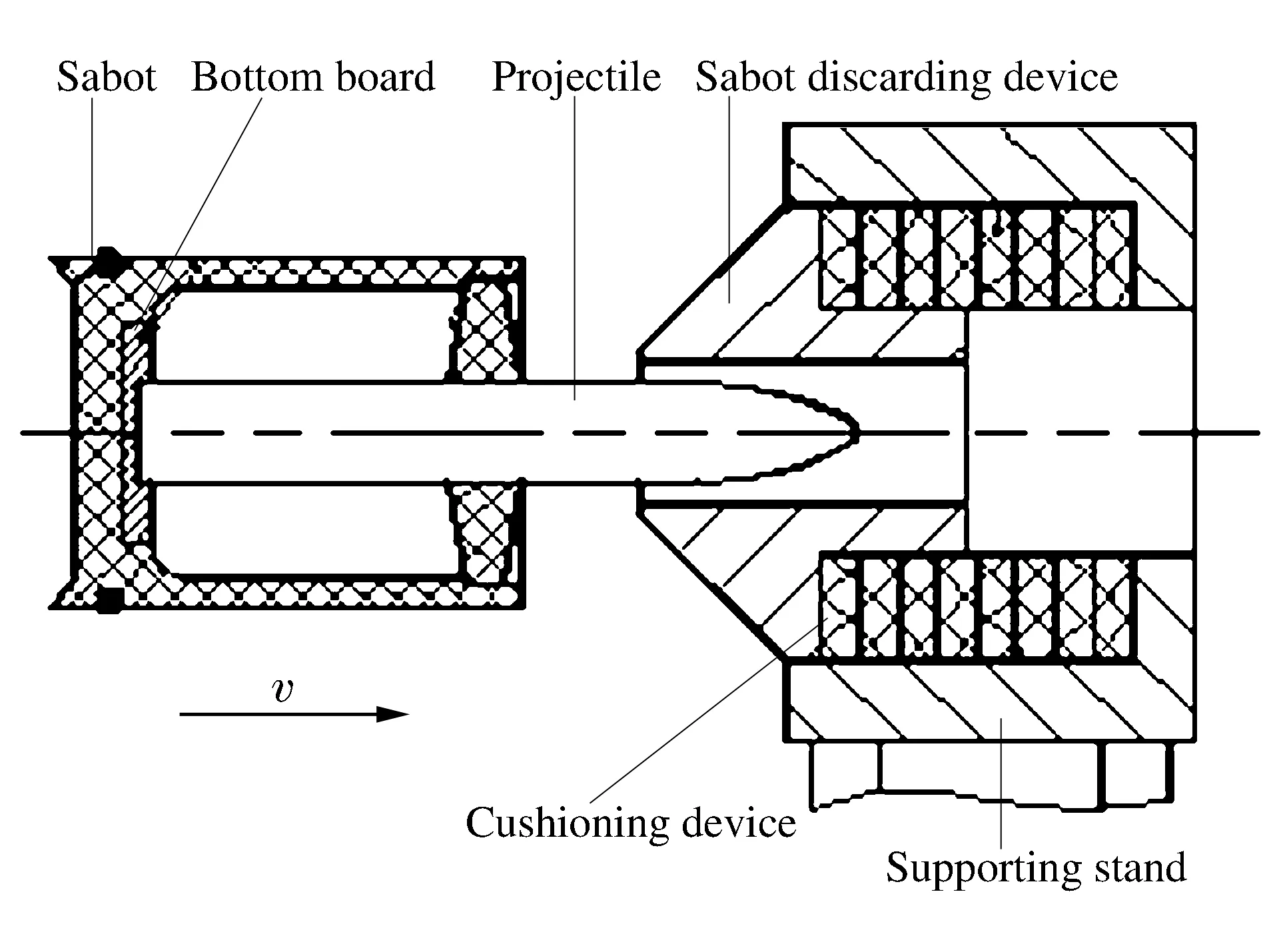
圖2 脫殼過程示意圖Fig.2 Schematic diagram of sabot discarding

1.2 彈體

小尺寸模擬彈直徑為50 mm，長度為416 mm，重量約3.6 kg，彈體內裝填模擬裝藥，如圖3所示。彈體材料采用30CrMnSiNi2MoVE高強鋼，熱處理后的材料力學性能分別為：抗拉強度1 680 MPa，屈服強度1 510 MPa，延伸率14%，沖擊功72 J，斷裂韌性112 MPa·m1/2。

1.3 靶體

圓柱形鋼筋混凝土靶的設計強度為30和60 MPa，體積配筋率為0.2%。靶板直徑為1.0 m，厚度為0.7 m，傾角為35°和45°。為減小彈體侵徹過程對混凝土靶邊界效應的影響，圓柱靶周圍用5 mm厚的鋼箍加固，如圖4所示。

混凝土靶板制作中，水泥、水和骨料含量依據國軍標GJB 1112-91《軍用機場場道工程施工及驗收規范》。混凝土靶板在標準溫度、濕度條件下養護28 d。實驗前對加工的鋼筋混凝土靶進行強度檢測，強度分別為31.5和61.8 MPa。

圖3 實驗彈體Fig.3 Experimental penetrator

圖4 實驗用鋼筋混凝土靶Fig.4 Experimental reinforced concrete targets

2 結果及分析

2.1 結果

進行了20余發實驗彈撞擊鋼筋混凝土靶板實驗，撞靶速度范圍為250～430 m/s，撞靶傾角范圍為30°～45°。圖5給出了彈體分別在約250和420 m/s速度下撞擊30 MPa鋼筋混凝土靶未跳彈和跳彈情況的典型實驗圖片。

圖5 彈丸侵徹30 MPa鋼筋混凝土靶Fig.5 Penetrators impacting 30 MPa reinforced concrete target

彈體侵徹60 MPa鋼筋混凝土靶板實驗11發，速度約260、310、340、380和420 m/s。約260 m/s速度下的打靶實驗3發：第1發實驗靶板傾角設計為30°，彈體撞靶速度為258 m/s，彈體撞靶后未發生跳彈，侵入混凝土靶中；根據第1發實驗結果，調整靶板傾角至33°，然后進行第2發打靶實驗，彈體以254 m/s的速度撞擊靶板，由于鋼筋的約束，彈體恰好嵌在靶板內部，根據彈道分析，彈體接近臨界跳彈；然后繼續調整靶板傾角至36°，又進行了第3發打靶實驗，彈體在257 m/s速度下撞擊靶板，撞靶后彈體明顯跳彈，彈體穿入防護鋼靶中。約310 m/s速度下的彈體打靶實驗2發：第1發實驗彈體以308 m/s 速度、35°傾角撞擊靶板，撞靶結束后，彈體落入靶箱內，根據彈道分析，彈體未發生跳彈，但由于沒有外力約束，實驗彈從混凝土靶中滑落；第2發實驗彈體以312m/s 速度、38°傾角撞擊靶板，撞靶后彈體跳彈，并侵入混凝土靶板上方的防護鋼靶中。約340 m/s速度下的彈體打靶實驗2發：第1發實驗彈體以342 m/s速度、36°傾角撞擊靶板，彈體撞擊靶板后，未發生跳彈；然后增加彈體撞靶傾角至39°，進行第2發實驗，實驗彈體以338 m/s 速度、39°傾角撞擊靶板，彈體基本處于臨界跳彈狀態。約380 m/s速度下侵徹鋼筋混凝土靶板實驗2發：第1發實驗彈體撞靶速度為388 m/s，撞靶傾角為40°，撞靶結束后彈體侵入靶中；調整彈體撞靶傾角至42°后進行第2發實驗，彈體以383 m/s的速度撞擊靶板，發生跳彈。約420 m/s速度下的彈體打靶實驗2發：第1發實驗彈體以426 m/s速度、43°傾角撞擊混凝土靶板，彈體跳彈；第2發實驗彈體撞靶傾角設計為42°，彈體以425 m/s速度撞擊靶板后發生臨界跳彈，并侵入到防護鋼靶中。

彈體侵徹30 MPa鋼筋混凝土靶板實驗10發，速度約260、300、340、380和420 m/s。約260 m/s速度下的實驗2發：第1發實驗彈體撞靶速度257 m/s、撞靶傾角36°，實驗后彈體侵入靶中，彈體在靶中的垂直侵徹深度約11 cm，彈道長度約42 cm；第2發實驗彈體撞靶速度256 m/s、撞靶傾角40°，實驗后彈體明顯跳彈。約300 m/s速度下的實驗2發：第1發實驗的彈體撞靶速度和撞靶傾角分別為304 m/s和38°，實驗后彈體侵入靶中；第2發實驗的彈體撞靶速度和傾角為302 m/s和41°，實驗后彈體跳彈，落入靶箱中。約340 m/s速度下的實驗2發：第1發實驗彈體以343 m/s速度、39°傾角撞擊靶板后，彈體侵入靶板中，未發生跳彈；調整撞靶角度進行第2發實驗，彈體以342 m/s速度、42°傾角撞擊靶板，彈體跳彈。約380 m/s速度下的實驗2發：第1發彈體以377 m/s速度、41°傾角撞擊靶板后，未產生跳彈；第2發彈體以379 m/s速度、44°傾角撞擊靶板后，發生跳彈。約420m/s速度下的實驗2發：第1發實驗彈體撞靶速度432 m/s、撞靶傾角42°，撞靶后彈體滯留在靶板內，彈軸與水平方向夾角65°；第2發實驗彈體撞靶速度417 m/s、撞靶傾角45°，實驗后彈體跳彈，落入靶箱內。

2.2 分析

2.2.1 實驗結果分析

如果每隔1°進行一次彈體侵徹實驗，直至相鄰兩發實驗有跳彈和未跳彈情況出現，這樣，可以把彈體臨界跳彈角度控制在1°范圍以內。但是，這樣需進行大量的實驗。可通過對彈體侵徹靶板彈道分析，如果能夠在2°～3°范圍內近似給出每組實驗下的彈體臨界跳彈角度，然后進行數據擬合，根據擬合曲線，可近似分析出彈體的臨界跳彈角度。

通過對上述實驗結果及彈體侵徹彈道綜合分析，可分別得到彈體侵徹60和30 MPa鋼筋混凝土靶的臨界跳彈角度。在260、310、340、380和420 m/s速度下，彈體侵徹60 MPa鋼筋混凝土的臨界跳彈傾角角度分別約為34°、37°、39°、41°和42°。在260、300、340、380和420 m/s速度下，彈體侵徹30 MPa鋼筋混凝土的臨界跳彈傾角角度分別約為38°、40°、42°、43°和44°。

2.2.2 經驗結果分析

采用球形空腔理論模型[7]，對彈體斜侵徹靶板過程進行了受力分析，并開展了大量不同尺寸縮比彈在200～860 m/s速度下的侵徹實驗(實驗數量近百發)。結合實驗結果，擬合給出了彈丸末端姿態角ζ與初始傾角β和侵徹能力參數P′的半經驗公式：

ζ=c0βc1P′c2

(1)

P′=P/d

(2)

式中：c0、c1和c2是量綱一系數，c0=e1.27，c1=0.99，c2=-0.26；d為彈體直徑(m)；P為彈體侵徹深度(m)；P′為量綱一參量，定義為彈體侵徹能力準數；β為初始傾角(彈體速度方向與靶面法向的夾角)；ζ為彈體姿態角(彈體軸線與靶面法向的夾角)。其中P由Young方程計算求得。

Young方程是由C.W.Young[8-11]在3 000多次實驗的基礎上統計分析得到、用來預估鉆地彈侵徹深度的經驗方程。Young方程的具體形式如下：

(3)

式中：m為彈體質量(kg)；A為彈體橫截面積(m2)；S為可侵徹性指標，與混凝土的配筋率、強度等參數有關；N為彈頭形狀影響系數；K為侵徹修正系數，與彈體質量有關。

研究表明，在一定速度范圍內，當彈體侵徹靶板過程中的末端彈體姿態角大于70°時，彈體開始發生跳彈。可確定當姿態角ζ為70°對應的初始傾角β，作為彈體臨界跳彈傾角。根據上述公式，可計算出不同速度下彈體分別侵徹30和60 MPa鋼筋混凝土的臨界跳彈傾角。

2.2.3 結果對比分析

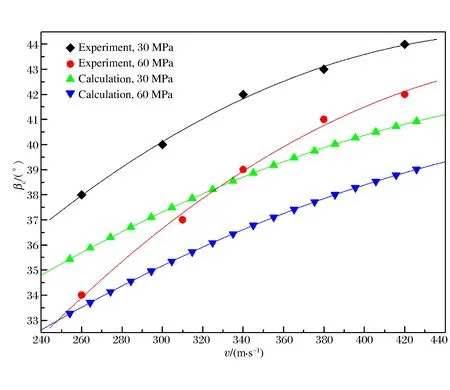
圖6 彈體臨界跳彈傾角角度與速度關系曲線Fig.6 Relation curves of projectile’s critical ricochet oblique angles and penetration velocities

根據實驗和計算分析得到，彈體在250～430 m/s速度下分別侵徹30和60 MPa鋼筋混凝土靶的臨界跳彈角度，如圖6所示。

相對于實驗結果，經驗公式計算得到的彈體的臨界跳彈傾角角度偏低，但偏差不超過3°，且實驗結果與經驗分析結果的臨界跳彈角度變化趨勢基本一致。隨著侵徹速度的增加，彈體的臨界跳彈角度變大，且彈體臨界跳彈角度隨速度增加而增大的變化趨勢逐漸變緩。這說明隨速度的增加，彈體臨界跳彈角度存在上限。可以想象，在不考慮彈體結構強度情況下，其臨界跳彈角度上限為90°，彈體軸線與靶面平行。此種情況下，無論速度多高，彈體都不會對目標進行侵徹，也就是說彈體發生了跳彈。

3 結 論

采用實驗和經驗分析的方法，對長徑比為8.32的彈體在250～430 m/s速度下分別侵徹30和60 MPa鋼筋混凝土靶的臨界跳彈角度進行了研究，結論如下。

(1)彈體侵徹相同強度靶板，隨著侵徹速度的增加，彈體的臨界跳彈傾角角度變大，且彈體臨界跳彈傾角角度隨速度增加而增大的變化趨勢逐漸變緩。

(2)彈體在相同速度下侵徹不同強度靶板，隨著靶板強度的增加，彈體的臨界跳彈傾角角度變小。

(3)實驗分析得到的彈體在250～430 m/s速度下侵徹30 MPa鋼筋混凝土的臨界跳彈角度范圍為38°～44°，侵徹60 MPa鋼筋混凝土的臨界跳彈角度范圍為34°～42°；經驗公式分析得到的彈體在250～430 m/s速度下侵徹30 MPa鋼筋混凝土的臨界跳彈角度范圍為36°～41°，侵徹60 MPa鋼筋混凝土的臨界跳彈角度范圍為34°～39°；經驗公式分析得到的彈體臨界跳彈角度結果偏低于實驗結果，但偏差基本在3°以內。

(4)實驗結果與經驗分析結果有一定的偏差，且實驗得到的彈體臨界跳彈角度結果大于經驗分析結果，分析造成這一差別的原因如下：實驗所采用的靶板為鋼筋混凝土靶，靶板中的鋼筋對彈體侵徹過程彈道偏轉有約束作用，可抑制彈體發生跳彈，從而提高了彈體的臨界跳彈角度；而經驗公式是根據彈體侵徹素混凝土靶(靶中無配筋)實驗結果建立的，相對于鋼筋混凝土靶，素混凝土靶中無鋼筋對彈體侵徹過程的偏轉進行約束，導致彈體侵徹素混凝土靶的臨界跳彈角度小些。因此，經驗公式適合于彈體侵徹素混凝土靶的臨界跳彈分析，而對于彈體侵徹鋼筋混凝土靶的臨界跳彈分析，實驗結果更接近實際。

結合實驗和經驗公式分析結果，可對彈體侵徹混凝土靶的臨界跳彈角度進行計算、分析，給出彈體有效侵徹靶板目標的角度范圍，為進行戰斗部作戰指導提供技術依據。

[1] Kanchibotla S. Modeling fines in blast fragmentation and its impact on crushing and grinding[C]∥A Conference on Rock Breaking. Kalgoorlie, Australia, 1999:37-44.

[2] Goldsmith W. Non-ideal projectile impact on targets[J]. International Journal of Impact Engineering, 1999,22(2/3):95-395.

[3] Frew D J, Forrestal M J, Hanchak S J. Penetration experiments with limestone targets and ogive-nose steel projectiles[J]. Journal of Applied Mechanics, 2000,67(4):841-845.

[4] Lee W, Lee H J, Shin H. Ricochet of a tungsten heavy alloy long-rod projectile from deformable steel plates[J]. Physics of Journal D: Applied Physicss, 2002,35(20):2676-2686.

[5] 劉晉.跳彈機理研究與數值模擬[D].太原:中北大學,2011.

[6] 吳榮波,陳智剛,王慶華.入射角對跳彈現象影響的數值模擬[J].設計與研究,2011,38(10):18-21. Wu Rongbo, Chen Zhigang, Wang Qinghua. Numerical simulation on the impact effect of incidence angle impacting ricochet[J]. Design and Research, 2011,38(10):18-21.

[7] Forrestal M J, Tzou D Y. A spherical cavity-expansion penetration model for concrete targets[J]. International of Solid Structures, 1997,34(31):4127-4146.

[8] Young C W. Depth prediction for earth-penetrating projectiles[J]. International of the Soil Mechanics and Foundations Division, 1969,95(3):803-817.

[9] Young C W. Development of empirical equation for predicting depth of an earth penetrating projectile[R]. SC-DR-67-60, 1967.

[10] Young C W. Equation for predicting earth penetration by projectiles: An update[R]. SAND-88-0013, 1988.

[11] Young C W. Penetration equations[R]. SAND-97-2426, 1997.

(責任編輯 丁 峰)

Critical ricochet performance of penetrator impacting concrete targets

Duan Jian, Wang Kehui, Zhou Gang, Xue Binjie,Chu Zhe, Li Ming, Dai Xianghui, Geng Baogang

(NorthwestInstituteofNuclearTechnology,Xi’an710024,Shaanxi,China)

The critical ricochet angle of a penetrator impacting hard targets obliquely needs to be analyzed and estimated to ensure that no ricochet occur while the penetrator hits the targets. In this work the experiments on the ricochet performance of the penetrator with a big length-to-diameter ratio impacting reinforced concrete targets at a velocity of 250-430 m/s were conducted, the critical ricochet angles in which it impacts the reinforced concrete targets possessing a compressive strength of 30 MPa and 60 MPa respectively were analyzed and estimated, and the envelope curves of the critical ricochet angle were obtained. The results show that, when the intensity of the target is maintained the same, the projectile’s critical ricochet angle increases with the increase of the penetration velocity. This increase gradually slows down. At the same penetration velocity, with the increase of the targets’ strength, the projectile’s critical ricochet angle decreases. The projectile’s critical ricochet angles from the analysis of the empirical formula were lower than those from the experiments, but the deviation is less than 3°.

mechanics of explosion; ricochet performance; penetrating warhead; concrete target; critical ricochet angle

10.11883/1001-1455(2016)06-0797-06

2015-04-17； < class="emphasis_bold">修回日期：2015-07-21

2015-07-21

段 建(1979— )，男，博士研究生，副研究員，duanjian@nint.ac.cn。

O385 <國標學科代碼：1303530 class="emphasis_bold"> 國標學科代碼：1303530 文獻標志碼：A國標學科代碼：1303530

A