爆炸荷載作用下巖石動(dòng)態(tài)裂紋擴(kuò)展的數(shù)值模擬*

鐘波波,李 宏,張永彬

(大連理工大學(xué)海岸和近海工程國(guó)家重點(diǎn)實(shí)驗(yàn)室，遼寧 大連 116024)

爆炸荷載作用下巖石動(dòng)態(tài)裂紋擴(kuò)展的數(shù)值模擬*

鐘波波,李 宏,張永彬

(大連理工大學(xué)海岸和近海工程國(guó)家重點(diǎn)實(shí)驗(yàn)室，遼寧 大連 116024)

運(yùn)用巖石破裂過(guò)程分析軟件RFPA-dynamic，就爆炸荷載的加載速率、炮孔到自由邊界的距離以及兩炮孔中間空孔的大小對(duì)動(dòng)態(tài)裂紋擴(kuò)展方式的影響進(jìn)行了研究。結(jié)果表明：隨著加載速率的減小，炮孔周圍的破碎區(qū)逐漸減少；裂紋開始萌生的位置逐漸由破碎區(qū)外邊緣向炮孔孔壁轉(zhuǎn)移；萌生的分支小裂紋逐漸減少，主裂紋擴(kuò)展長(zhǎng)度逐漸增大。由于自由邊界的影響，炮孔向下擴(kuò)展的裂紋逐漸彎向水平方向，且炮孔到自由邊界的距離越小，這種趨勢(shì)越明顯。由于空孔的導(dǎo)向作用，使靠近空孔的裂紋逐漸彎曲向空孔處擴(kuò)展，同時(shí)在空孔孔壁兩端產(chǎn)生一條向炮孔擴(kuò)展的裂紋；空孔半徑大小對(duì)裂紋的導(dǎo)向作用，并無(wú)明顯的影響；材料的非均勻性，對(duì)裂紋的擴(kuò)展方式有顯著的影響。

固體力學(xué)；裂紋擴(kuò)展；RFPA-dynamic；爆炸應(yīng)力波；空孔

在采礦工程、石油開采工程及地震預(yù)測(cè)等領(lǐng)域中，常常關(guān)注裂紋、空孔、夾雜物等爆破結(jié)構(gòu)或材料中的原始缺陷，對(duì)介質(zhì)中應(yīng)力波傳播方式的影響。尤其在巷道或隧道的開挖中，常設(shè)置一些空孔，利用空孔的應(yīng)力集中效應(yīng)、自由面效應(yīng)和卸壓效應(yīng)，以提高爆破效果。空孔在爆破過(guò)程的作用機(jī)理，有了大量的研究。S.H.Cho等[1]通過(guò)數(shù)值模擬的方法，研究了不同波形和自由邊界對(duì)動(dòng)態(tài)裂紋擴(kuò)展過(guò)程的影響，并討論了巖石的非均勻性對(duì)斷裂模式的影響；S.H.Cho等[2]通過(guò)DFPA軟件研究了兩端帶有刻痕的空孔對(duì)動(dòng)態(tài)裂紋擴(kuò)展過(guò)程的控制作用，并討論了空孔位置、兩炮孔起爆時(shí)間誤差和材料非均勻性對(duì)裂紋擴(kuò)展的影響；Z.Aliabadian等[3]采用二維動(dòng)態(tài)離散元方法研究了預(yù)裂爆破方法，主要考慮的參數(shù)是應(yīng)力張量和壓裂模式，結(jié)果表明爆炸荷載的大小和炮孔間距非常重要；李啟月等[4]運(yùn)用LS-DYNA，模擬了槽孔與不同直徑空孔的動(dòng)態(tài)破碎貫通過(guò)程，分析了不同直徑空孔引起的空孔效應(yīng)及其對(duì)槽腔巖石破壞和槽腔成型的促進(jìn)作用；岳中文等[5]采用新型數(shù)字激光動(dòng)態(tài)焦散線實(shí)驗(yàn)系統(tǒng)，以PMMA為實(shí)驗(yàn)材料，對(duì)爆炸荷載作用下空孔周圍的動(dòng)應(yīng)力場(chǎng)分布及空孔對(duì)爆生主裂紋擴(kuò)展行為的影響進(jìn)行了研究。

由于巖石是一種非均勻材料，其斷裂過(guò)程依賴于應(yīng)變率的大小，其空孔作用機(jī)理復(fù)雜、設(shè)置靈活，所以對(duì)空孔周圍應(yīng)力場(chǎng)變化過(guò)程和動(dòng)態(tài)裂紋擴(kuò)展方式進(jìn)行研究有著重要的理論意義和工程價(jià)值。本文中，選用RFPA-dynamic分析系統(tǒng)，就爆炸荷載加載速率、炮孔到自由邊界距離以及兩炮孔中間空孔大小對(duì)動(dòng)態(tài)裂紋擴(kuò)展方式的影響進(jìn)行研究。該程序可以以一個(gè)應(yīng)力波或初始速度作為輸入，按照時(shí)間步長(zhǎng)進(jìn)行逐步分析，在每個(gè)時(shí)間步內(nèi)，考慮質(zhì)量和加速度對(duì)于力學(xué)平衡的影響，用彈性動(dòng)力有限元程序進(jìn)行應(yīng)力分析，用最大拉應(yīng)力準(zhǔn)則和摩爾庫(kù)侖準(zhǔn)則判斷單元是否損傷，從而可以再現(xiàn)巖石這種非均勻材料在爆炸荷載作用下的動(dòng)態(tài)裂紋擴(kuò)展過(guò)程。

1 模 型

RFPA-dynamic分析系統(tǒng)規(guī)定應(yīng)力以壓為正，拉為負(fù)，相關(guān)詳情請(qǐng)參見文獻(xiàn)[6-8]。

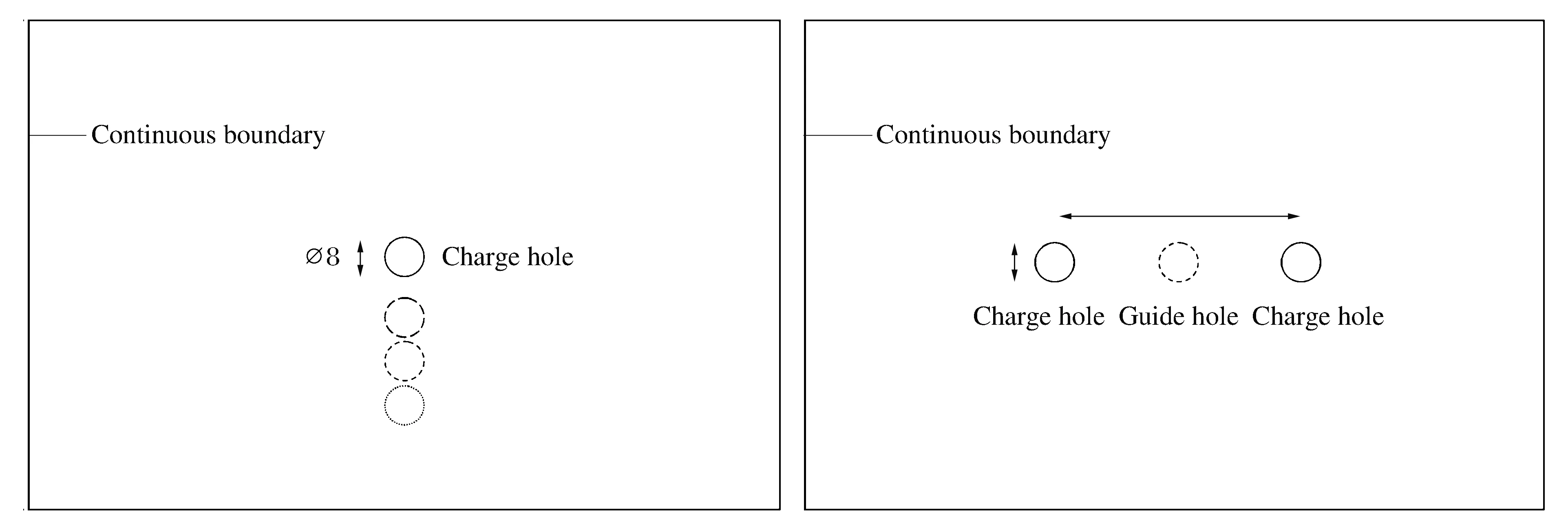
圖1 分析模型幾何示意圖Fig.1 Schematic geometry for analysis model

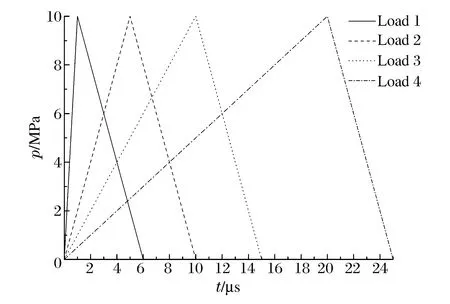
圖2 施加荷載的壓力曲線Fig.2 Pressure curves for applied pressure waveforms

模型如圖1所示，尺寸為200 mm×100 mm，劃分為500×250=125 000個(gè)單元，炮孔半徑r0均為4 mm。圖1(a)中，炮孔到自由邊界距離l分別為35、30、25 mm；圖1(b)中，兩個(gè)炮孔間距s為50 mm，兩炮孔中間空孔半徑r2分別為2、4、6 mm。施加的爆炸荷載如圖2所示，荷載峰值都為10 MPa，荷載上升時(shí)間分別為1、5、10、20 μs，荷載從峰值衰減到零的時(shí)間不變，均為 5 μs。為了計(jì)算的精確性，動(dòng)態(tài)時(shí)間步長(zhǎng)取為0.2 μs。

研究爆炸荷載加載速率和空孔大小對(duì)動(dòng)態(tài)裂紋擴(kuò)展方式的影響時(shí)，模型邊界都為連續(xù)邊界條件，應(yīng)力波不發(fā)生反射；研究炮孔到自由邊界距離對(duì)動(dòng)態(tài)裂紋擴(kuò)展方式的影響時(shí)，模型底邊為自由邊界，應(yīng)力波可以發(fā)生反射，其余邊界仍為連續(xù)邊界。采用平面應(yīng)變模型，進(jìn)行分析。

計(jì)算參數(shù)分別為：P波波速vP=5.00 km/s，S波波速vS=2.89 km/s，密度ρ=2.7 t/m3，彈性模量E=56 GPa，泊松比ν=0.25，抗壓強(qiáng)度T=75 MPa，壓拉比η=15，均質(zhì)系數(shù)m=5。為了考慮材料的非均勻性，假設(shè)基質(zhì)單元的彈性模量及強(qiáng)度等力學(xué)參數(shù)服從Weibull分布函數(shù)，即：

(1)

式中：m為均質(zhì)系數(shù)，反映巖石材料力學(xué)性質(zhì)的均質(zhì)度，m越小則巖石的性質(zhì)越不均勻；α0為反映巖石材料平均性質(zhì)的參數(shù)。有關(guān)上述分布函數(shù)和參數(shù)的定義及選取方法參見文獻(xiàn)[9-10]。

2 結(jié) 果

2.1 單孔

2.1.1 爆炸荷載加載速率對(duì)動(dòng)態(tài)裂紋擴(kuò)展方式的影響

4種加載速率下最大主應(yīng)力分布及裂紋擴(kuò)展方式，如圖3所示。從圖3中可以看出，隨著加載速率的減小，炮孔周圍的破碎區(qū)逐漸減小，裂紋開始萌生的位置逐漸改變。第1種加載速率下，炮孔周圍形成一圈破碎區(qū)，裂紋開始萌生的位置為破碎區(qū)的外邊緣；第4種加載速率下，炮孔周圍未能形成破碎區(qū)，裂紋開始萌生的位置為炮孔孔壁；第2、3種加載速率下，破碎區(qū)范圍逐漸減少，裂紋開始萌生的位置逐漸由破碎區(qū)的外邊緣向炮孔孔壁轉(zhuǎn)移。這個(gè)現(xiàn)象主要是由于，隨著加載速率的減小爆炸荷載引起的應(yīng)力波作用逐漸減弱，當(dāng)加載速率很小時(shí)，裂紋萌生就會(huì)類似于炮孔孔壁受法向均勻靜荷載時(shí)的情況。從圖3中還可以發(fā)現(xiàn)，隨著加載速率的減小，萌生的分支小裂紋逐漸減少，而主裂紋擴(kuò)展的長(zhǎng)度逐漸增大。上述模擬結(jié)果與文獻(xiàn)[1]所得到的結(jié)論基本一致。

圖3 不同加載速率下最大主應(yīng)力分布及裂紋擴(kuò)展Fig.3 Maximum principal stress distribution and crack propagation at different loading rates

2.1.2 炮孔到自由邊界距離對(duì)動(dòng)態(tài)裂紋擴(kuò)展方式的影響

只施加第1種荷載，將炮孔到自由邊界的距離分別取為35、30和25 mm，結(jié)果如圖4所示。根據(jù)應(yīng)力波傳播理論，當(dāng)應(yīng)力波傳播到自由面時(shí)，壓縮應(yīng)力波反射為拉伸應(yīng)力波，產(chǎn)生拉應(yīng)力。該拉應(yīng)力與先前的壓應(yīng)力疊加，使靠近自由面單元的徑向壓應(yīng)力減小。當(dāng)反射回來(lái)的拉伸應(yīng)力波幅值大于先前入射的壓縮應(yīng)力波幅值時(shí)，在靠近自由面的區(qū)域內(nèi)就會(huì)出現(xiàn)只有拉應(yīng)力的情況。根據(jù)最大拉應(yīng)力瞬時(shí)斷裂準(zhǔn)則[11]，一旦拉應(yīng)力達(dá)到或超過(guò)材料的抗拉臨界值時(shí)，就會(huì)發(fā)生層裂。

從圖4中可以發(fā)現(xiàn)，炮孔處向下擴(kuò)展的裂紋逐漸彎向水平方向，且隨著炮孔到自由邊界距離的減小，這種趨勢(shì)更加明顯，說(shuō)明自由表面的存在對(duì)裂紋擴(kuò)展方向產(chǎn)生了明顯的影響。炮孔到自由邊界越近，應(yīng)力波傳播到自由面位置的幅值就越大，相應(yīng)地反射產(chǎn)生的拉應(yīng)力幅值也就越大，層裂現(xiàn)象越明顯。當(dāng)炮孔到自由邊界的距離較小時(shí)，炮孔處擴(kuò)展的裂紋與層裂產(chǎn)生的裂紋在自由面附近，更易于互相搭接和貫通。

圖4 炮孔到自由邊界不同距離下最大主應(yīng)力分布及裂紋擴(kuò)展Fig.4 Maximum principal stress distribution and crack propagation of different distance from charge hole to free boundary

2.2 雙孔

2.2.1 爆炸應(yīng)力波與空孔相互作用的理論依據(jù)

炮孔爆炸后，向周圍巖石施加沖擊荷載，沖擊波向外傳播而不斷衰減，最后變成應(yīng)力波。當(dāng)應(yīng)力波傳播到空孔孔壁表面時(shí)，在空氣與介質(zhì)的分界面處，將產(chǎn)生透射與反射。下面分析應(yīng)力波垂直傳播到空孔孔壁時(shí)，即正入射時(shí)，模型中反射波的情況。

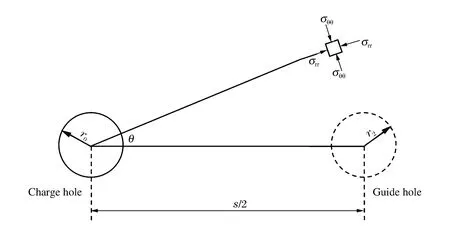
圖5 空孔應(yīng)力集中作用分析圖Fig.5 Concentrated effect of stress around guide hole

如圖5所示，炮孔起爆后，在其周圍介質(zhì)中激起爆炸應(yīng)力波，并向外傳播，隨著傳播距離的增加，應(yīng)力峰值衰減規(guī)律為[12]：

(2)

式中：σr為介質(zhì)中某點(diǎn)的爆炸附加徑向應(yīng)力；σθ為介質(zhì)中某點(diǎn)的爆炸附加環(huán)向應(yīng)力；p0為炸藥爆炸后作用于孔壁的初始?jí)毫Γ籸0為炮孔半徑；r為介質(zhì)中某點(diǎn)到炮孔中心的距離；α為應(yīng)力波衰減系數(shù)[12]，α=2±(ν/1-νd)；νd為介質(zhì)的動(dòng)態(tài)泊松比，工程爆破加載速率范圍內(nèi)的動(dòng)態(tài)泊松比與靜態(tài)泊松比ν的關(guān)系為νd=0.8ν；λd為動(dòng)態(tài)側(cè)應(yīng)力系數(shù)，λd=ν/(1-νd)。

當(dāng)應(yīng)力波傳到空孔孔壁時(shí)，由于應(yīng)力波的反射，空孔孔壁附近的應(yīng)力將比無(wú)空孔時(shí)大，表現(xiàn)為空孔的應(yīng)力集中效應(yīng)。根據(jù)彈性力學(xué)理論，空孔附近的峰值應(yīng)力狀態(tài)表示為：

(3)

式中：σrr為空孔應(yīng)力集中后介質(zhì)中的徑向應(yīng)力；σθθ為空孔應(yīng)力集中后介質(zhì)中的環(huán)向應(yīng)力；r2為空孔半徑；R為介質(zhì)中某點(diǎn)到空孔中心的距離；θ為計(jì)算點(diǎn)到炮孔中心連線與炮孔和空孔連線的夾角；κ=r2/R。

對(duì)上式求dσθθ/dθ，令dσθθ/dθ=0，得θ=0,±π，可知徑向應(yīng)力、環(huán)向應(yīng)力及剪切應(yīng)力的最大值均出現(xiàn)在炮孔與空孔連線方向上。此時(shí)：

(4)

在空孔孔壁上時(shí)，r2=R，即κ=1，得：

(5)

2.2.2 空孔大小對(duì)動(dòng)態(tài)裂紋擴(kuò)展方式的影響

空孔在爆破中有著重要地位，特別是在控制定向爆破中對(duì)應(yīng)力波具有導(dǎo)向作用，這點(diǎn)已得到了證明[4-5]。

圖6(a)～(c)分別為半徑2、4和6 mm空孔在第1種荷載作用下的最大主應(yīng)力分布及其裂紋擴(kuò)展方式。從圖中可以看到，炮孔起爆后，伴隨著應(yīng)力波由炮孔逐漸向外傳播，在炮孔周圍逐漸形成破碎區(qū)，裂紋在破碎區(qū)邊緣開始萌生、擴(kuò)展；當(dāng)應(yīng)力波傳播到空孔孔壁時(shí)，小部分應(yīng)力波發(fā)生反射，反射波與之后的入射波疊加，相當(dāng)于在空孔孔壁處產(chǎn)生了卸荷作用，大部分應(yīng)力波繼續(xù)向外傳播，與另外炮孔產(chǎn)生的應(yīng)力波疊加，疊加部位壓應(yīng)力幅值增加；炮孔周圍萌生的裂紋呈放射狀向外擴(kuò)展，但由于空孔的導(dǎo)向作用，使靠近空孔的裂紋逐漸彎曲向空孔處擴(kuò)展，同時(shí)在空孔孔壁兩端產(chǎn)生一條向炮孔擴(kuò)展的裂紋。可見，空孔半徑對(duì)裂紋的導(dǎo)向作用并無(wú)明顯的影響，這與文獻(xiàn)[13]的研究結(jié)果基本一致。半徑4、6 mm空孔孔壁裂紋的萌生位置大約在與炮孔中心連線處，這與上述理論分析一致。而半徑2 mm空孔的卻不在中心連線處，這是由于當(dāng)空孔半徑較小時(shí)，非均勻性對(duì)它的影響比大孔徑空孔的大。

圖6(d)為均質(zhì)系數(shù)25、半徑2 mm空孔模型的最大主應(yīng)力分布及裂紋擴(kuò)展方式。通過(guò)與圖6(a)作對(duì)比，發(fā)現(xiàn)：當(dāng)均質(zhì)系數(shù)增大時(shí)，分支小裂紋減少，以擴(kuò)展長(zhǎng)度基本相同的主裂紋為主，且裂紋較平直光滑；兩炮孔裂紋萌生位置和擴(kuò)展方式基本一樣。由于炮孔各方向受力相同，當(dāng)材料較均勻時(shí)，裂紋萌生、擴(kuò)展具有對(duì)稱性。圖6(d)中大約在空孔與炮孔中心連線上萌生了兩條裂紋，且很平直地向炮孔方向擴(kuò)展。這個(gè)現(xiàn)象與上述的彈性理論較吻合，同時(shí)說(shuō)明了考慮材料非均勻性的重要意義。

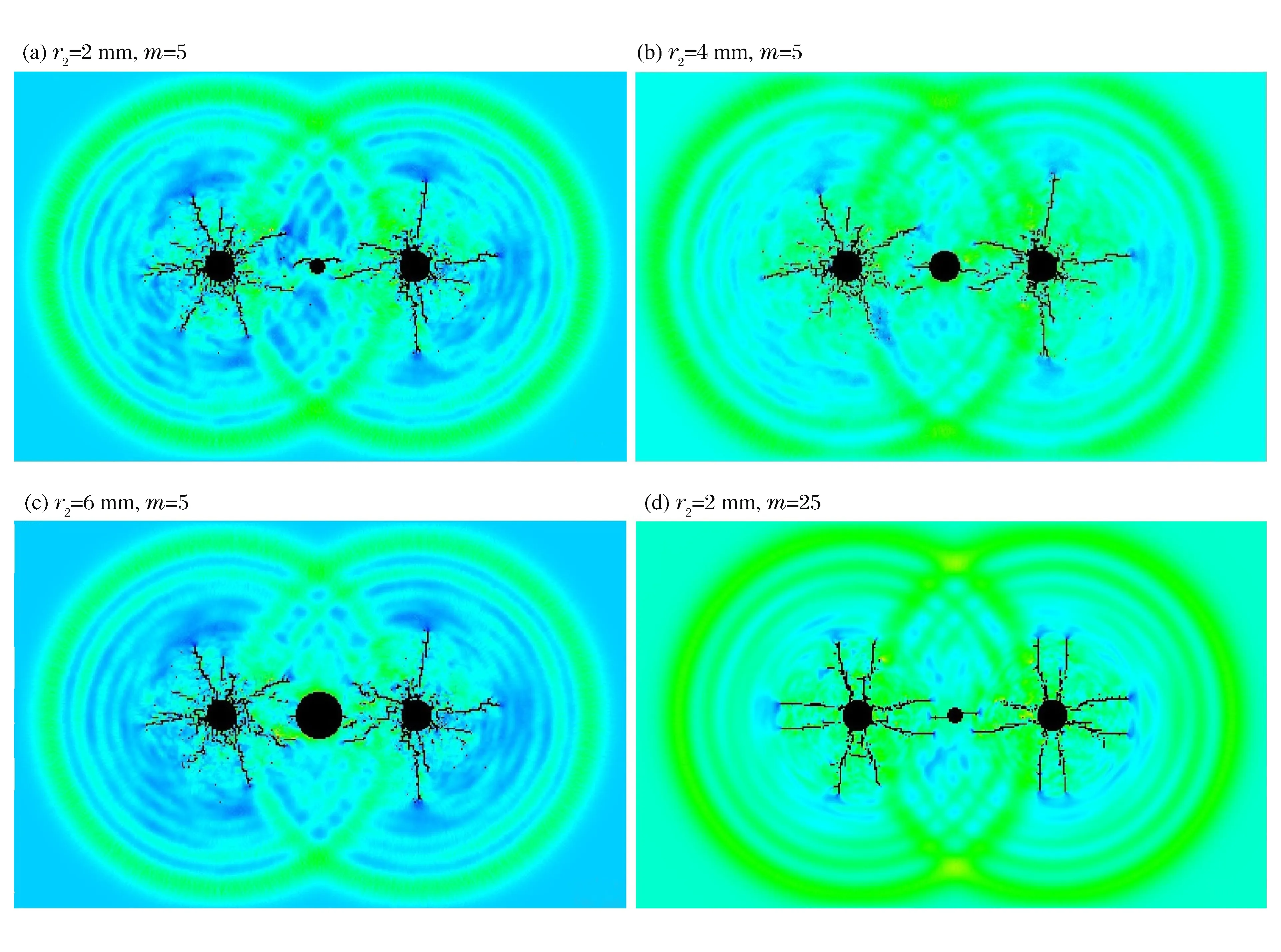
圖6 不同半徑空孔的最大主應(yīng)力分布及裂紋擴(kuò)展Fig.6 Maximum principal stress distribution and crack propagation of different guide holes

2.2.3 空孔孔壁單元的主應(yīng)力曲線

圖7為與左炮孔中心連線處、距空孔孔壁1.2 mm處一個(gè)單元的主應(yīng)力曲線，該空孔半徑為4 mm。可以清楚看到應(yīng)力波的傳播、反射和疊加：隨著應(yīng)力波從炮孔向空孔的傳播，單元最大主應(yīng)力從零開始逐漸增大到1 MPa，到達(dá)A點(diǎn)后，由于爆炸荷載開始衰減和反射的拉應(yīng)力與入射的壓應(yīng)力疊加的雙重作用，主應(yīng)力開始下降；B點(diǎn)為臨界點(diǎn)，由于拉應(yīng)力隨著反射波的增多而增大，主應(yīng)力開始反向增大，C點(diǎn)為最大主應(yīng)力反向的最大值，約為1 MPa；C點(diǎn)到D點(diǎn)之間，由于右炮孔產(chǎn)生的應(yīng)力波傳播到了空孔左孔壁附近，導(dǎo)致主應(yīng)力曲線出現(xiàn)小幅度的波動(dòng)；從D點(diǎn)所對(duì)應(yīng)時(shí)間的最小主應(yīng)力云圖可以發(fā)現(xiàn)，由于左右炮孔向外傳播的應(yīng)力波和空孔孔壁反射的應(yīng)力波相互疊加、炮孔輻射狀裂紋尖端的應(yīng)力集中及破壞單元周圍的應(yīng)力釋放，空孔孔壁周圍形成了一個(gè)拉應(yīng)力集中區(qū)，當(dāng)拉應(yīng)力達(dá)到試樣的抗拉強(qiáng)度(5 MPa)時(shí)，裂紋開始萌生(E點(diǎn))；裂紋一旦萌生，單元應(yīng)力迅速降到零。

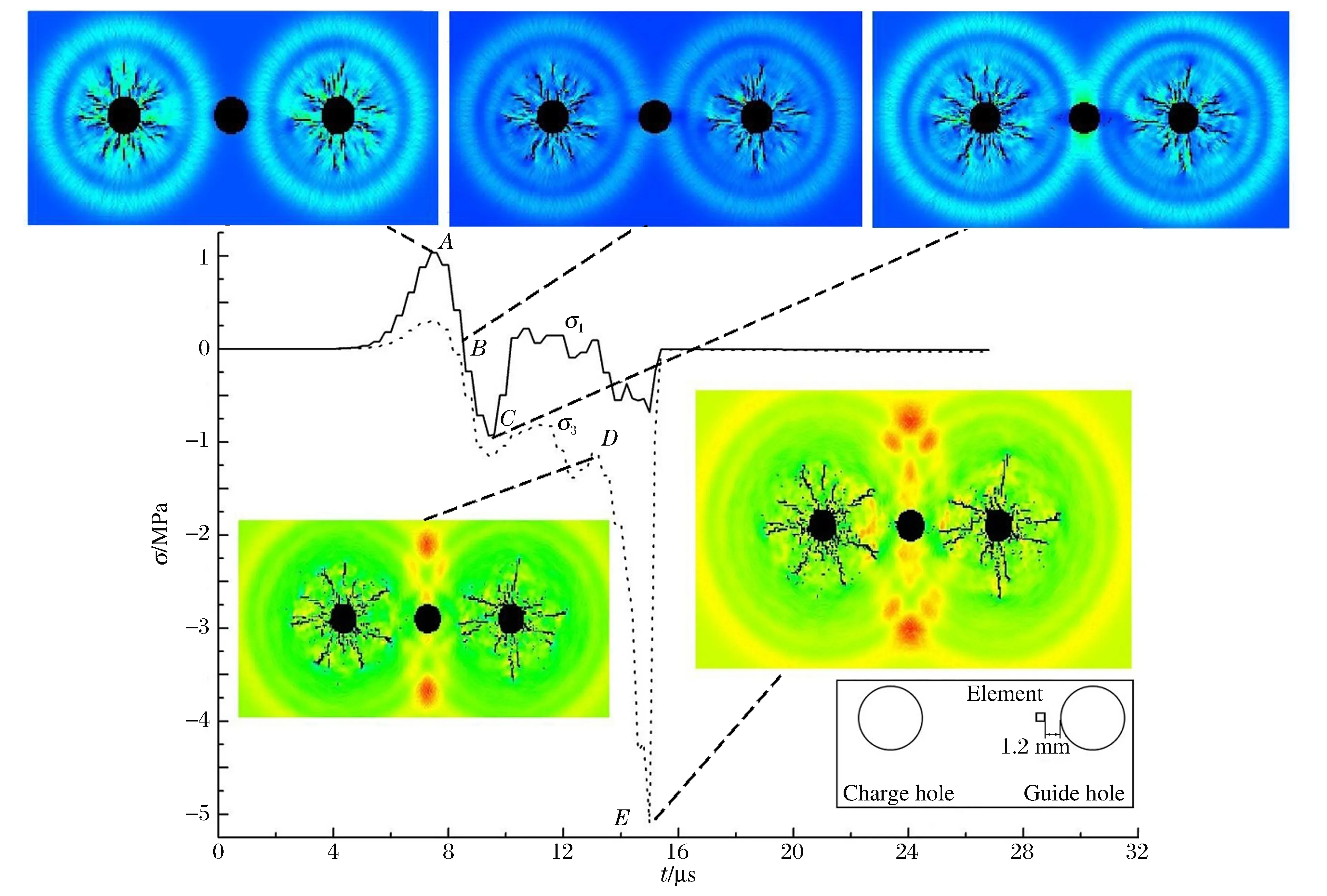
圖7 單元的主應(yīng)力曲線Fig.7 The principal stress curves of the element

3 結(jié) 論

炮孔周圍為連續(xù)邊界條件時(shí)，在爆炸荷載作用下，隨著加載速率的減小，炮孔周圍的破碎區(qū)逐漸減少，裂紋開始萌生的位置逐漸由破碎區(qū)外邊緣向炮孔孔壁轉(zhuǎn)移，孔壁周圍萌生的分支小裂紋逐漸減少，主裂紋擴(kuò)展長(zhǎng)度逐漸增大。炮孔周圍存在自由邊界時(shí)，由于自由面的影響，炮孔向下擴(kuò)展的裂紋逐漸彎向水平方向，且炮孔到自由邊界的距離越小，這種趨勢(shì)越明顯，加上層裂的作用，自由面附近的裂紋更易于互相搭接、擴(kuò)展和貫通。當(dāng)兩炮孔中間有一個(gè)空孔時(shí)，由于空孔的導(dǎo)向作用，使炮孔向空孔方向擴(kuò)展的裂紋，逐漸彎曲向空孔處擴(kuò)展，但空孔半徑大小對(duì)裂紋的導(dǎo)向作用，并無(wú)明顯的影響，同時(shí)大約在空孔與炮孔中心連線上，空孔孔壁兩端萌生了向炮孔處擴(kuò)展的裂紋，由于材料的非均勻性，裂紋的萌生位置和擴(kuò)展方式與彈性理論解有著些許的不同。由空孔孔壁處單元的主應(yīng)力時(shí)程曲線可以發(fā)現(xiàn)，孔壁裂紋是由于空孔周圍的拉應(yīng)力集中而萌生的。

[1] Cho S H, Kaneko K. Influence of the applied pressure waveform on the dynamic fracture processes in rock[J]. International Journal of Rock Mechanics and Mining Sciences, 2004，41(5)：771-784.

[2] Cho S H, Nakamura Y, Mohanty B, et al. Numerical study of fracture plane control in laboratory-scale blasting[J]. Engineering Fracture Mechanics, 2008，75(13)：3966-3984.

[3] Aliabadian Z, Sharafisafa M. Numerical modeling of presplitting controlled method in continuum rock masses[J]. Arabian Journal of Geosciences, 2013，7(12)：5005-5020.

[4] 李啟月，徐敏，范作鵬，等.直眼掏槽破巖過(guò)程模擬與空孔效應(yīng)分析[J].爆破，2011，28(4)：23-26. Li Qiyue, Xu Min, Fan Zuopeng, et al. Simulation of rock failure process in cutting by parallel hole and analysis on empty hole effect[J]. Blasting, 2011，28(4)：23-26.

[5] 岳中文，郭洋，許鵬，等.定向斷裂控制爆破的空孔效應(yīng)實(shí)驗(yàn)分析[J].爆炸與沖擊，2015，35(3)：304-311. Yue Zhongwen, Guo Yang, Xu Peng, et al. Analysis of empty hole effect in directional fracture controlled blasting[J]. Explosion and Shock Waves, 2015，35(3)：304-311.

[6] Chau K T, Zhu W C, Tang C , et al. Numerical simulations of failure of brittle solids under dynamic impact using a new computer program: DIFAR[J]. Key Engineering Materials, 2004，261/263(1)：239-244.

[7] Zhu W C, Tang C A, Huang Z P, e t al. A numerical study of the effect of loading conditions on the dynamic failure of rock[J]. International Journal of Rock Mechanics and Mining Sciences, 2004，41(3)：424-424.

[8] Zhu W C, Tang C A. Numerical simulation of Brazilian disk rock failure under static and dynamic loading[J]. International Journal of Rock Mechanics and Mining Sciences, 2006，43(2)：236-252.

[9] 唐春安.巖石聲發(fā)射規(guī)律數(shù)值模擬初探[J].巖石力學(xué)與工程學(xué)報(bào)，1997，16(4)：368-374. Tang Chun’an. Numerical simulation of AE in rock failure[J]. Chinese Journal of Rock Mechanics and Engineering, 1997，16(4)：368-374.

[10] Tang C. Numerical simulation of progressive rock failure and associated seismicity[J]. International Journal of Rock Mechanics and Mining Sciences, 1997，34(2)：249-261.

[11] 王禮立，朱兆祥.應(yīng)力波基礎(chǔ)[M].2版.北京：國(guó)防工業(yè)出版社，2005.

[12] 戴俊.柱狀裝藥爆破的巖石壓碎圈與裂隙圈計(jì)算[J].遼寧工程技術(shù)大學(xué)學(xué)報(bào)(自然科學(xué)版)，2001，20(2)：144-147. Dai Jun. Calculation of radii of the broken and cracked areas in rock by a long charge explosion[J]. Journal of Liaoning Technical University (Natural Science), 2001，20(2)：144-147.

[13] 文梼，譚海.巖石爆破中的空孔效應(yīng)數(shù)值計(jì)算分析[J].爆破，2011，28(3)：58-61. Wen Tao, Tan Hai. The empty hole effect numerical computation analysis during rock blasting[J]. Blasting, 2011，28(3)：58-61.

(責(zé)任編輯 丁 峰)

Numerical simulation of dynamic cracks propagation of rock under blasting loading

Zhong Bobo, Li Hong, Zhang Yongbin

(StateKeyLaboratoryCoastalandOffshoreEngineering,DalianUniversityofTechnology,Dalian116024,Liaoning,China)

The influences of the blast loading rate, the distance from the guide hole to the free boundary and the radius of the guide hole between the two charge holes, on the dynamic propagation of cracks in rock were studied using realistic failure process analysis (RFPA-dynamic). The results show that, as the loading rate decreases, the crushed zone around the charge hole is gradually reduced; the position of the crack initiation moves gradually from the crushed zone to the charge hole; and the number of small branch cracks gradually decreases while the length of the main crack increases. Due to the influence of the free boundary, the cracks that were previously downward now gradually bend in the horizontal direction, and this tendency becomes more observable as the distance from the charge hole to the free boundary gets shorter. As a result of the guidance of the guide hole, the cracks close to the guide hole gradually curve to the guide hole and, at the same time, a crack is formed at both ends of the guide hole wall that propagates to the charge hole. The radius of the guide hole has no obvious effect on the guiding role, but the nonuniformity of the material does have a significant effect on the way the cracks propagate.

solid mechanics; crack propagation; RFPA-dynamic; explosive stress wave; guide hole

10.11883/1001-1455(2016)06-0825-07

2015-04-15； < class="emphasis_bold">修回日期：2015-06-29

2015-06-29

國(guó)家重點(diǎn)基礎(chǔ)研究發(fā)展計(jì)劃(973計(jì)劃)項(xiàng)目(2014CB047100,2011CB013503)

鐘波波(1990— )，男，碩士研究生,ytgczbb@163.com。

O346.1 <國(guó)標(biāo)學(xué)科代碼：1301545 class="emphasis_bold"> 國(guó)標(biāo)學(xué)科代碼：1301545 文獻(xiàn)標(biāo)志碼：A國(guó)標(biāo)學(xué)科代碼：1301545

A