計及設備故障檢修的電網可靠性和經濟性分析

張　煦，張向伍(.江蘇無錫供電公司，江蘇無錫4000；.河南南陽供電公司，河南南陽473000)

?

計及設備故障檢修的電網可靠性和經濟性分析

張煦1，張向伍2
(1.江蘇無錫供電公司，江蘇無錫214000；2.河南南陽供電公司，河南南陽473000)

摘要：電力設備在服役期間受到老化、磨損或天氣等運行工況的影響，故障率隨時間增長具有累積效應。全面分析影響各類電力設備可靠性的主要因素，建立了計及運行工況的時變故障率模型；在此基礎上，考慮各計劃檢修等級對電力設備可靠性的不同改善程度，利用役齡回退模型構建了A，C 2個重要檢修等級下的電力設備故障率函數，并推導了各類電力設備平均無效度公式，進而得到系統可靠性/經濟性指標解析表達式。最后通過可靠性測試（RBTS）系統驗證評估方法的有效性，并對RBTS發電機系統進行了靈敏度分析。

關鍵詞：運行工況；A，C級檢修；役齡回退；平均無效度；靈敏度分析

電力系統中各類電力設備如發電機、變壓器和線路等在運行中都受到自身老化、機械磨損、溫度和天氣等運行工況的影響，其風險水平隨著服役時間的增加逐漸累積增長[1]。目前國內電力企業為改善電力設備可靠性主要采用計劃檢修和狀態檢修方式[2]，但是由于狀態檢修依賴于先進的狀態監測和狀態評價技術，監測裝置本身又存在故障的可能以及狀態評價技術尚不成熟等因素限制了狀態檢修方式的應用。計劃檢修能有效延緩電力設備劣化趨勢，成為提高供電可靠性最常采用的技術手段。計劃檢修延緩電力設備劣化過程主要體現在計劃檢修能延緩老化，削弱甚至徹底消除磨損和其他隱性因素，改善電力設備運行狀態。目前計劃檢修對電力設備故障率削減程度模型具體基于兩大類。一類是采用概率方法，認為電力設備經計劃檢修后以一定概率“恢復如新”[3]；另一類則基于役齡回退模型[4]，由于故障率是關于設備服役時間的函數，役齡回退模型則認為設備經檢修后的恢復效果相當于設備役齡回退至之前某個時刻點，該模型使得設備經過檢修后的恢復效果介于“恢復如新”和“恢復如舊”之間，更貼近實際檢修效果，本文也采用該模型開展研究。

目前電力企業對各類電力設備實施了A，B，C，D 4個檢修等級[5，6]其中C級檢修為電網年度性常規檢修，而A級檢修對設備進行全面徹底解體檢查和修復，本文選取A，C 2個最具有代表性的等級構建多級檢修模型，以此為基礎，結合役齡回退模型開展多級檢修可靠性、經濟性評估。

1　計及運行工況的電力設備故障率模型

1.1發電機的故障率函數

影響發電機可靠性的因素大體可分為3類。

（1）發電機發熱老化、機械磨損導致運行狀態逐漸惡化，故障率隨服役時間逐漸攀升，可用β1=1的二重復合威布爾函數λg1（t）近似描述[7]；

（2）電壓、頻率異常波動引起的發電機保護動作，考慮到電壓、頻率的波動具有隨機性，因而可采用一恒定故障率λg2表示；

（3）惡劣環境等外界因素造成的發電機停運，因為同樣具有偶然性，因此也可以采用一恒定故障率λg3來描述。

綜上可得發電機故障率模型為：

式（1）中：α1≥0，α2≥0為二重威布爾函數的尺度參數；β2≥0為形狀參數。

1.2變壓器的故障率函數

變壓器在服役過程中受到老化、保護誤動和人為誤操作等多種內、外因素的影響，其中外因部分保護誤動、人為誤操作對變壓器故障率的影響同發電機第（2），（3）類停運因素的分析一樣，同樣可分別用一恒定值λt2，λt3描述。而內因隨時間具有累積效應，是導致變壓器停運的重要因素，目前我國多為油浸式變壓器，失效的主要原因是絕緣性能的劣化，描述該內因對變壓器故障率貢獻的模型[8]，即：

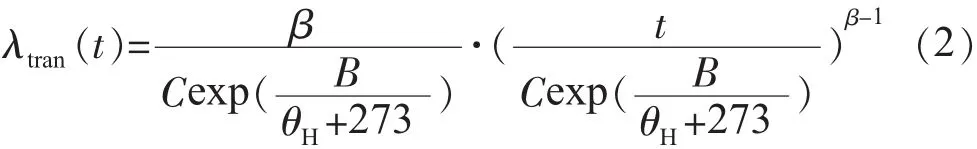
式（2）中：B，C為經驗值；θH為熱點溫度；β為形狀參數；t為變壓器在熱點溫度θH下的持續運行時間。其中θH與變壓器負載率K和環境溫度θA有關，其計算模型及公式參照文獻[9]。

綜上變壓器故障率模型如下：

1.3架空線路的故障率函數

架空線路老化故障率增長的主要原因是抗拉強度的損失[8]，可用β1=1的二重復合威布爾函數描述。此外，由于架空線路屬于暴露型元件[10]，故障率受天氣影響顯著，惡劣天氣將大幅增加失效概率，因而線路故障率函數為：

式（4）中：η1，η2為天氣對輸電線路故障率的影響因子，正常天氣下η1=1，η2=1。

2　各類電力設備平均無效度計算

本文依據檢修等級的不同修復程度，設A級檢修為使設備“恢復如新”的完全檢修方式，事后檢修為使設備“修復如舊”的最小檢修方式，C級檢修為介于2者之間的不完全檢修方式，則A級、C級檢修下故障率曲線如圖1所示。

圖1　A/C級檢修方式下設備故障率曲線

假設電力設備的A級、C級檢修周期比率為N，即進行1次A級檢修前有N-1次C級檢修，并設C級檢修周期為T，第i次C級檢修前有效役齡為h（i），第i-1至i次C級檢修間的故障率函數為λ（i）（t），役齡回退因子為k（i-1），考慮到C級檢修效果隨著次數的增加改善效果逐漸變差，即0=k（0）≤k（1）…≤k（N-1）≤1。則：

式（5，6）中：

則A級檢修期間內平均停運時間TOut為：

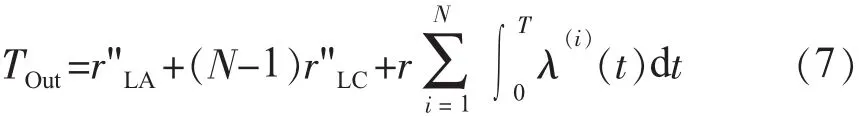
式（7）中：r"LA為平均A級檢修時間；r"LC為平均C級檢修時間；r為平均事后檢修時間。T，TOut，r"LA，r"LC，r的單位均為h，λ（i）（t）單位為次/h。

根據平均無效度概念，其定義為給定時間TTut內平均不可用時間TOut與TTot的比值，結合式（6）、式（7），可得平均無效度Q為：

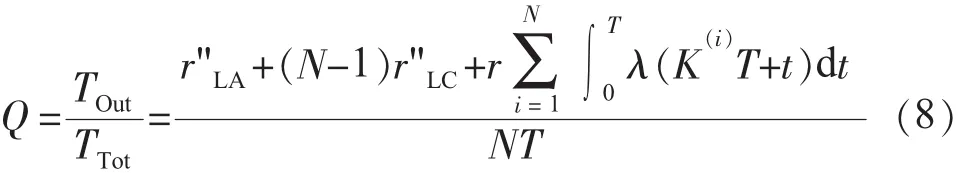
下面針對第1節建立的各類設備故障率模型，利用式（8）推導其平均無效度。

（1）計及多級檢修的發電機平均無效度。將式（1）代入式（8）可得：

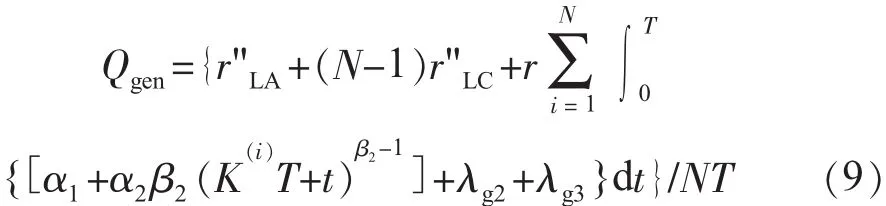
（2）計及多級檢修的變壓器平均無效度。通過變壓器的日典型負載率曲線，日典型溫度曲線，利用文獻[9]的方法可算得變壓器熱點溫度曲線。在此基礎上將熱點溫度進行聚類，獲得一組典型熱點溫度（tH1，tH2，…，tHm）及其對應的概率（P1，P2，…，Pm），通過該組熱點溫度和式（3）可計算對應故障率函數（λtra1（t），λtra2（t），…，λtram（t））。則A級檢修期間變壓器平均無效度為：

（3）計及計劃檢修的輸電線路平均無效度。采用基于正常、惡劣天氣的兩狀態天氣模型描述天氣對輸電線路故障率的影響，并設惡劣天氣向正常天氣的轉移率為μ，正常天氣向惡劣天氣的轉移率為λ。則A級檢修期間輸電線路平均無效度為：

3　系統可靠性與經濟性指標

本文第1節根據各電力設備運行工況的不同和對可靠性影響因素的差異，建立了發電機、變壓器、架空線路的故障率函數模型；第2節進一步考慮不完全檢修模式，基于平均無效度概念，推導了各電力設備平均無效度解析表達式。本節在前兩節的基礎上，利用解析方法求取系統可靠性、經濟性指標以及靈敏度指標，便于全面分析電力系統可靠性和經濟性，找出影響系統總成本的關鍵設備，為電網經濟性改善提高有益參考。

設某電力系統的元件數目為M，元件狀態分別為S1，S2，…，SM，且相互獨立。元件k處于正常狀態記為Sk=0，故障狀態記為Sk=1，則系統狀態x=（S1，S2，…，SM）的概率表示為：

結合第2節推導的平均無效度公式，多級檢修模式下系統可靠性指標ILOLP，IEENS的解析表達式為：

系統總成本包括2個部分，即檢修成本和停電成本。則其中系統停電成本COut為：

式（15）中：Cunit為單位停電成本，萬元/（MW·h）。

假設電力設備k單次A級檢修成本為CLAk，單次C級檢修成本為CLCk，單次事后檢修成本為CCORk，則系統總檢修成本CREP為：

綜上可得系統總成本CTotal表示為：

根據系統總成本CTotal解析表達式，可推導出系統總成本對元件k的C級檢修周期Tk的靈敏度：

本文通過電力系統可靠性、經濟性指標以及靈敏度指標來分析電力系統可靠性和經濟性水平。指標計算的基本思路是采用狀態枚舉法枚舉電力系統的故障系狀態，通過直流最優削負荷模型篩選出需要全部或部分停電的系統狀態，并計算出相應的削負荷量，從而得到一組故障系統狀態向量和相應削負荷量的向量，結合各電力設備平均無效度，計算系統可靠性和經濟性指標，最后通過系統總成本對C級檢修周期求導的方式反映各設備C級檢修周期調整對系統總成本的改善程度。其流程圖如圖2所示。

圖2　電力系統可靠性及經濟性評估流程圖

4　算例分析

本文針對可靠性測試（RBTS）[11]開展A級、C級檢修的可靠性、經濟性評估方法研究。設備檢修費用包括材料費和施工費，發電機C級檢修材料費可參考文獻[12]，線路C級檢修材料費為0.1萬元/km，施工費設為0.02萬元/h。假設二重威布爾函數參數α1，α2分別為原故障率0.6倍和0.3倍，取β2=3，λg2=0.5次/ a、λg3= 0.3次/ a；惡劣天氣對線路故障率的影響因子η1= 1.3，η2=1.1，單位時間內天氣轉移率λ= 0.007 9次/h，μ= 0.020 8次/h。設Cunit= 0.05萬元/（MW·h），事后檢修材料費取為C級檢修材料費的1/3倍，A級檢修材料費取為C級檢修材料費的3倍。

電力系統通常采取每年進行1次C級檢修、5年進行1次A級檢修的檢修模式，假設發電機A和C級檢修時間分別為事后檢修時間的1.2倍和1.0倍，線路的A級和C級檢修時間為事后檢修時間的1.5倍和1.2倍，設役齡回退因子為k（i）=i/（2i +3.2）。則RBTS在該檢修模式下的可靠性、經濟性評估結果以及RBTS系統總成本相對于各發電機C級檢修周期的靈敏度分別如表1、表2所示。

表1　A/C級檢修方式下系統可靠性/經濟性指標

（1）本文從可靠性和經濟性2個方面對RBTS系統進行了全面分析，ILOLP，IEENS反映了系統的可靠性水平，而停電成本CTotal也是可靠性水平的體現，同時將可靠性水平轉換成停電成本形式能直觀與檢修成本形成比較，從表1可以看出，RBTS系統檢修成本達到805.65萬元，占到了系統總成本的84%。

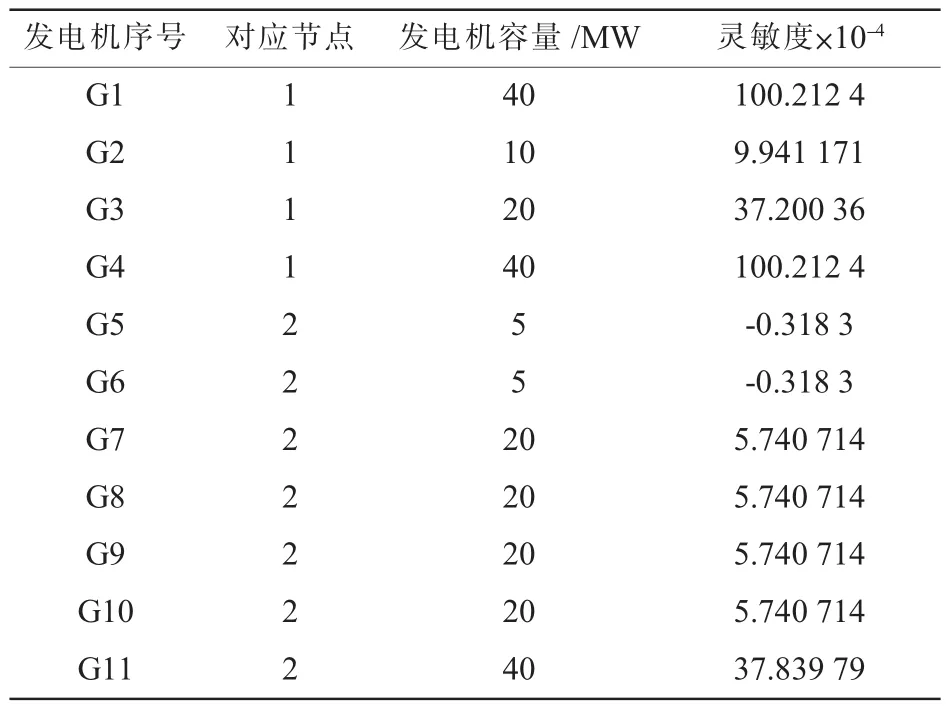
表2　RBTS總成本相對于各發電機C級檢修周期的靈敏度

（2）通過表2中RBTS系統各發電機的靈敏度分析分結果可以看出，系統內的大機組如G1，G4的靈敏度最大，系統內小機組G5，G6靈敏度最小。表明調整系統內大機組C級檢修周期對系統總成本CTotal的影響最大，原因在于系統內大機組的可靠性優劣對系統充裕度影響最大，從而影響系統的停電成本，最終影響系統總成本。

（3）此外通過G5（節點1），G6（節點1）與G11（節點2）的靈敏度比較表明即使相同容量和可靠性的機組，在電網拓撲中的位置不同，對系統成本的影響也不盡相同。因此在優化調整電力設備計劃檢修周期時，不能單從設備本身出發進行調整，而應計入電網拓撲對系統充裕度的影響。

5　結束語

本文計及運行工況因素，構建了各類電力設備故障率函數模型，并基于役齡回退因子建立了電力設備多級檢修模型；推導了系統可靠性/經濟性指標關于C級檢修周期和A/C級檢修周期比率的解析表達式。本文計及設備檢修的可靠性、經濟性評估方法對RBTS系統進行了算例計算，結果表明該方法能較為全面有效地反映系統可靠性和經濟性水平，找到可靠性水平和檢修成本占系統總成本的比重，便于設備檢修投入的宏觀把控。

同時，通過靈敏度分析得出系統內大機組由于能顯著影響系統充裕度，從而對系統總成本影響最大，改善系統經濟性應該首先考慮大機組檢修周期的調整。此外，電網拓撲結構也對系統充裕度有較大影響，優化調整檢修周期時應該綜合考慮設備本身容量和可靠性和設備在電網拓撲中的位置。

參考文獻：

[1] CHEN Y, WANG Z L, QIU J, etal. Adaptive Bathtub Hazard Rate Curve Modeling Via Transformed Radial Basis Functions[C]. International Conference on Quality, Reliability, Risk, Maintenance, and Safety Engineering, 2011：110-114.

[2]唐燕，劉艷.考慮電網總風險和檢修收益的設備狀態檢修計劃優化[J].電力系統保護與控制，2014，42(9)：33-39.

[3] SHEU S H, CHANG T H. Generalized Sequential Preventive Maintenance Policy of a System Subject to Shocks[J]. International Journal of Systems Science, 2002，33(3)：267-276.

[4] MARTORELL S, SANCHEZ A, SERRADELL V. Age-dependent Reliability Model Considering Effects of Maintenance and Working Conditions[J]. Reliability Engineering&System Safety, 1999，64(1)：19-31.

[5] DL/T 838—2003發電企業設備檢修導則[S].中華人民共和國國家經濟貿易委員會，北京：中國電力出版社，2003.

[6] DL/T 573—2010電力變壓器檢修導則[S].國家能源局，北京：中國電力出版社. 2010.

[7]段東立，武小悅，鄧宏鐘.基于時變故障率與服務恢復時間模型的配電系統可靠性評估[J].中國電機工程學報，2011，31 (28)：57-63.

[8]何劍，程林，孫元章，等.條件相依的輸變電設備短期可靠性模型[J].中國電機工程學報，2009，29(7)：39-45.

[9] IEEE Working Group for Loading Mineral-Oil-Immersed Transformers．IEEE Std C57.91-1995 IEEE guide for loading mineraloil-immersed transformers[S]. 2012.

[10]寧遼逸，吳文傳，張伯明.電力系統運行風險評估中元件時變停運模型分析[J].電力系統自動化，2009，33(16)：7-12.

[11] BILLINTON R, KUMAR S, CHOWDHURY N, et al. A Reliability Test System For Educational Purposes-Basic Data [J]. IEEE Transactions on Power Systems.1989，04(3)：1238-1244.

[12]趙淵，張煦，楊清.基于可靠性成本/效益分析的電網計劃檢修周期優化[J].電力系統自動化，2014，38(20)：54-60.

張煦（1986），男，湖南邵陽人，工程師，研究方向為電力系統規劃與可靠性；

張向伍（1987），男，河南信陽人，工程師，研究方向為電力系統自動化。

Analysis for the Reliability and Economic of Power System Considering Maintenance

ZHANG Xu1, ZHANG Xiangwu2
(1.State Grid Wuxi Power Supply Company, Wuxi 214000, China；2.Stat Grid Nanyang Power Supply Company,Nanyang 473000, China)

Abstract：Electric power equipments suffer from aging, wearing, and weather conditions in operation, the failure rate has a cumulative effect over time. Considering the main factors affecting the reliability of various electric power equipments, the time-varying failure rate model based on the operating conditions is established. On this basis, the important A-level and C-level preventive maintenance modes which have different reliability improvements in each preventive maintenance levels are built based on the effective age, and the average unavailability formulas of kinds of power equipment is derived. Then, the analytical expressions for the system reliability and economy indices are established. Finally, According to the studies on RBTS, the validity of the algorithm is verified, and the sensitivity analysis of the generator system is carried out.

Key words：operating conditions; A-level and C-level preventive maintenance; the effective age; average unavailability; the sensitivity analysis

作者簡介：

收稿日期：2015-10-25；修回日期：2015-12-03

中圖分類號：TM73

文獻標志碼：A

文章編號：1009-0665（2016）02-0060-05