混凝土受力本構關系及展望

朱志永 金輝

1武漢平煤武鋼聯(lián)合焦化公司（430082）2河南建筑職業(yè)技術學院（450003）

混凝土受力本構關系及展望

朱志永1金輝2

1武漢平煤武鋼聯(lián)合焦化公司（430082）2河南建筑職業(yè)技術學院（450003）

通過混凝土本構模型的研究與分析，將混凝土本構模型分為以下幾類，根據其特點和作用解決工程中的相應問題，并將這些理論結合微觀觀察與分析作出對于未來的展望。

彈性本構模型；塑性本構模型；內蘊時間本構模型；斷裂力學本構模型；損傷力學本構模型

1 混凝土本構模型

混凝土是土木工程結構中應用極為廣泛的材料,在相當長時間內依靠經驗公式進行設計與分析。近幾十年來,隨著電子計算機的普及,混凝土非線性有限元分析得到了很大發(fā)展,有關混凝土的本構關系得到了廣泛而深入的研究。混凝土本構模型主要分為以下幾類：彈性本構模型、彈塑性本構模型、內蘊時間本構模型、斷裂力學本構模型、損傷本構模型以及各種模型組合而成的模型。

1.1 彈性本構模型

彈性力學模型是最早出現的材料本構模型也是最簡單的本構模型，在早期解決工程問題中起到了重要的作用。直至現在，較多的結構分析程序仍是采用的彈性模型。其典型特點是：除去外力變形恢復到初始狀態(tài)，變形可逆，不產生能量耗散。彈性模型又分為線彈性模型和非線性彈性模型。

1）線彈性本構模型

線彈性模型中，應力張量分量σij與應變張量分量εkl之間滿足線性關系，即廣義虎克定律：

式中，Cijkl是四階彈性剛度張量的分量，在最一般的情況下包括81個材料常數。如果材料是正交各向異性的，獨立的材料常數可減少至9個，如果材料是各向同性的，材料常數減少為兩個，可用彈性模量E和波松比ν來表示，此時，應力－應變關系可表達為：

線彈性虎克定律表達簡單，材料參數容易從簡單實驗測定，在混凝土結構分析中一直很有吸引力，尤其是在混凝土處于較低的應力狀態(tài)（開裂以前）可以取得滿足工程要求的計算結果，但在高應力狀態(tài)下誤差較大。

2）非線彈性本構模型

超過線彈性變形階段的混凝土在進一步受力過程中會產生明顯的不可逆變形，但如果僅考慮單調加載可以采用非線性彈性模型，因此將非線性彈性模型應用于混凝土只是一種近似。應力應變的非線性關系能較為精確的描述混凝土峰值應力前的變形特性，且計算簡單。這種模型又分為三種：

1）Cauchy非線彈性模型

這是最簡單的一種非線性彈性模型，是對線彈性模型的改進。該模型假定應力只依賴于應變，應變也只依賴于應力，與變化路徑無關，各向同性情況下全量形式的應力－應變表達式為：

該模型只是一種經驗模型，尤其適合于比例加載情況,但不嚴格滿足熱力學基本定律，不同加載路徑下得不到統(tǒng)一的應變能表達式，因此應力應變之間不存在功共軛關系。復雜加載條件下誤差較大。

2）Hyperelastic非線彈性模型

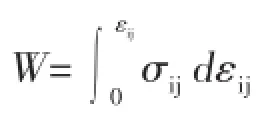
該模型滿足質量守恒定律，不僅能描述混凝土力－位移的非線性而且能描述混凝土的膨脹、應力引起的各向異性。Cauchy非線性彈性模型及Hyperelastic非線彈性模型在有限元模擬中可采用不斷變化的割線模量。較為著名的混凝土非線性彈性本構模型如Cedolin et al.模型,Kotsovos et al.模型,Ottosen模型等都是屬于此類采用全量型本構模型。

3）Hypoelastic非線彈性模型

該模型認為材料的力學性能不僅與現時應力及應變狀態(tài)有關，而且還與達到此狀態(tài)的變化路徑有關，為反映路徑相關性，一般采用增量形式表達應力－應變關系：

由于應力－應變關系采用增量形式表達，因此在有限元模擬中可采用不斷變化的切線模量，屬于此類的非線性彈性本構模型有著名的Darwin和Pecknold構本構模型（1977）以及Elwi和Murray模型（1979）。

彈性模型最大的缺點是：不能考慮加載過程中的不可逆變形,不能處理卸載以及循環(huán)加卸載情況。我國現行混凝土結構設計規(guī)范所采取的方法是：進行結構內力計算采用線彈性模型，而對于特別重要的或受力狀況特殊的大型桿系結構和二維、三維結構必要時尚應對結構整體或其部分進行受力全過程的非線性分析，而該非線性所采用的就是非線性彈性本構模型。

作為彈性模型的重要輔助控制部分，破壞準則是必不可少的。破壞準則可以理解為彈性材料的應力狀態(tài)上限，當應力狀態(tài)超出應力空間的破壞面時，混凝土失效并退出工作。上世紀60年代以來，各國學者在混凝土多軸強度實驗研究基礎上提出了多種破壞準則，破壞面由3～5個材料參數控制，代表性的有：Bresler-Pister準則、Reimann準則、Ottosen準則、Hsieh-Ting-Chen準則、Willam-Warnke準則、Kotsovos準則、Podgorski準則、過鎮(zhèn)海準則等。

1.2 塑性本構模型

以屈服函數為基礎的塑性理論在解決金屬類晶體延性材料問題方面取得了很大的成就。經典彈塑性理論主要指塑性增量理論（全量塑性理論僅能用于簡單加載情況，隨著數值方法及計算機技術的發(fā)展現已很少采用）是描述材料在塑性狀態(tài)應力與應變增量之間關系的本構理論，在實際數值方法中一般按加載過程積分獲得整個加載歷史的力－變形響應。塑性本構理論包括如下必不可少的組成部分：屈服準則、塑性流動準則（可以時相關聯(lián)或非相關聯(lián)的）、塑性強化準則以及加載－卸載準則。對某一特定的工程材料，采用不同的屈服函數及相應的塑性勢函數可以產生不同的塑性模型。

塑性理論經過數百年的發(fā)展，在各國學者不懈的努力下已經發(fā)展成為一套完整的理論體系，在數學表達上是嚴格的,不僅能合理用于各種金屬材料，而且經過修正可以廣泛適用于巖土及混凝土材料。傳統(tǒng)塑性理論的很多基本假設，如靜水壓力不影響屈服、體積變化是彈性的、剪應力不引起塑性體積變化、塑性應變增量與屈服面正交等是不適用于巖土、混凝土類材料的，塑性理論應用于摩阻類材料必須突破這些限制。廣義塑性理論成為解決這類問題的理論依據。

塑性理論用于混凝土最大也是最明顯的缺點就是不能很好地處理峰值應力后的軟化問題。這是因為按照Drucker公設，以定義在應力空間中的屈服函數為基礎的塑性模型只能處理穩(wěn)定材料（穩(wěn)定材料）問題，而按照Il’yushin公設，定義在應變空間的塑性模型則可以處理軟化問題，但缺乏應變空間屈服函數的實驗驗證，得不到廣泛的應用。而與損傷理論結合的塑性理論可通過損傷理論很好地解決軟化問題，這也是文章的主要任務。

較為著名的針對于混凝土的塑性模型主要有：Chen-Chen模型、Han-Chen模型、Chen模型、Fardis-Chen模型、Klinsinski-Mroz模型、Dvorkin模型、Read-Hegemier，Onateet al.模型、Pietruszczak et al.模型、Ohtani-Chen模型等。

1.3 內蘊時間本構模型

內蘊時間理論是一種基于不可逆熱力學框架的材料本構理論，由Valanis于1971年提出，我國學者范鏡泓為該理論的推廣做了大量的工作，具體研究了多種材料的本構模型，并對材料的本構不變性給予了數學證明。該理論的基本假設為：塑性和粘塑性等耗散材料內的任一點的現時應力狀態(tài)是該點鄰域內整個變形和溫度歷史的泛函，且該歷史是用一個取決于變形中的材料特性和變形程度的內蘊時間標度Z來度量的。

Valanis于1978年對該理論提出了一種新的定義，由于引起偏應變和體應變的機制不同，因此采用不同的內蘊時間來度量，各向同性情況下有：

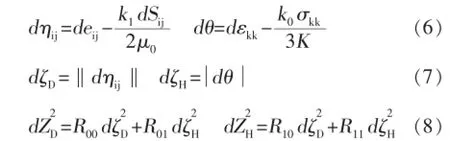
式中：μ0和K分別代表剪切彈性模量和體積彈性模量，k0，k1是系數,當k0=k1=1時,dηij，dθ分別為塑性偏應變分量與塑性體應變分量的增量，dζD為塑性應變空間的歐幾里得模型，dζH是塑性體積應變的絕對值。ζ為廣義內蘊時間量度，它通過一些反映材料性質變化及耦合效應的函數Rij以最后確定內蘊時間標度ZD和ZH。Rij是ζD和ζH以及其率的函數,R01和R10表示偏斜響應與體積響應的耦合效應。

當用于各向異性耗散材料時,內蘊時間量度ζD，ζH可統(tǒng)一表達為：

此時的內蘊時間標度表達為：

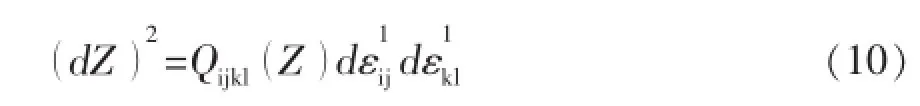
Qijkl（Z）是Z的函數，，為不可逆應變增量。于是，由本構方程形式不變性，并仿照線性粘彈性本構關系，可得到各向同性情況下的本構方程為：

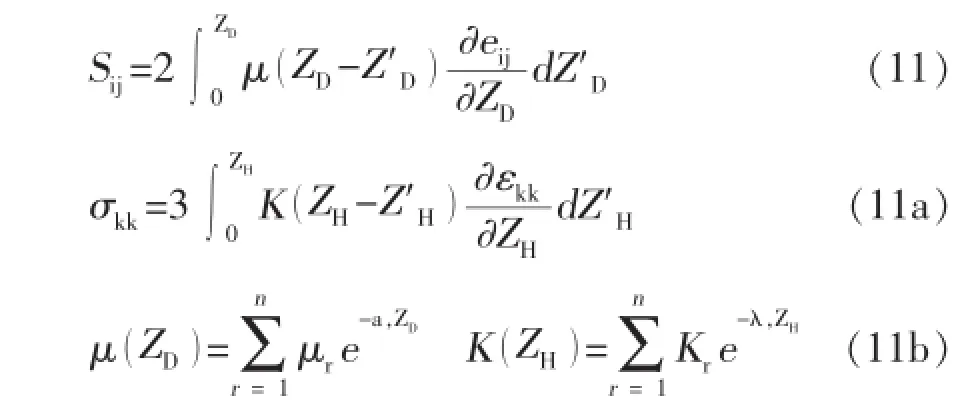
μ （ZD），K （ZH）分別為偏量張量空間和球量張量空間的核函數，且其初值μ0=μ(0)，K0=K(0)分別為初始剪切彈性模量和初始體積彈性模量，Sij為偏應力張量，eij為偏應變張量，σkk為體積應力，εkk為體積應變。

而各向異性情況下的本構方程可根據粘彈性力學基本公式表達為：

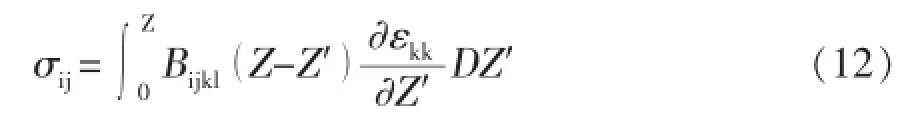
內蘊時間理論是以不可逆熱力學為基礎，理論基礎比較深厚,優(yōu)點是擺脫了屈服面的約束,在實際問題的計算中能用一個統(tǒng)一的公式描述全過程。根據本構方程形式不變性定律可利用已有理論的公式形式來給出本構方程,現在常用的是粘彈性公式形式,但并不局限于粘彈性公式形式。

內蘊時間理論是模仿Biot的線性粘彈性理論建立在Onsager不可逆熱力學的基礎之上,Onsager原理只在偏離平衡態(tài)不遠時才能適用，對于有限彈塑性變形，內蘊時間理論的適用性還需進一步討論。它對已知實驗的解釋程度，如何確定反映物質響應的積分核函數及物質所特有的內蘊時間,如何向大變形、大溫度方向推廣，以及如何進行有效的數值計算等問題，都需進一步研究。

最早把內蘊時間理論用于混凝土的是Bazant，Bazant的理論不涉及不可逆熱力學,而是直接采用內蘊時間的概念,用試湊法和參數優(yōu)化法得到參數值,他的模型能較好地模擬混凝土的性能,但是模型參數過多,而且一些參數有耦聯(lián)關系,一些參數缺乏物理意義,使用起來過于繁瑣。

1.4 斷裂力學本構模型

為正確地反映混凝土內部裂縫的開展規(guī)律，正確選擇一個建立在斷裂力學理論上的開裂模型是至關重要的。嚴格來說，斷裂力學不是一種材料的本構模型,但是斷裂理論與應力－應變空間彈塑性理論的組合彈塑性斷裂本構模型在預測一些典型的混凝土結構工作性能和強度方面發(fā)揮了重要作用。

斷裂力學基本理論基于脆性材料假定建立Griffith斷裂準則，并根據裂縫尖端應力和位移以確定該裂縫是繼續(xù)擴展還是閉合。如果裂縫周圍的材料不存在應力殘余,則認為該材料是線彈性的，可以采用線彈性斷裂力學以描述裂縫和材料的變形。然而，裂縫周圍區(qū)域材料往往會發(fā)生比較明顯的塑性變形，此時線彈性斷裂力學理論不適用。為此，學者們提出了非線性斷裂力學。目前，盡管大范圍屈服或非線性斷裂力學方法已經得到有力的開發(fā)和應用，但線彈性斷裂力學由于應用簡便、預測結果偏于保守的特點，仍在實際中有著廣泛的應用。1961年，Kaplan首先將斷裂力學引入混凝土中，其主要研究帶裂縫的混凝土體的強度和裂縫的傳播規(guī)律,從力學側面研究宏觀的斷裂現象，包括宏觀裂縫的形成、擴展、失穩(wěn)開裂、傳播以及止裂等。它著眼于混凝土體裂縫前緣附近的位移場、應力場、能量釋放率G來研究帶裂縫的構件強度、剛度和穩(wěn)定性，分析裂縫擴展穩(wěn)定性、擴展規(guī)律性，以建立宏觀裂縫起裂、裂紋的穩(wěn)定擴展和失穩(wěn)擴展的判據，判斷裂縫是否穩(wěn)定，進而探討如何控制和防止結構斷裂破壞的措施。

Y.Zaitsev和Nemat-Nasser等結合局部平均概念，在局部意義上利用斷裂力學基本理論對混凝土材料進行了分析，其結果表明，對于混凝土、巖石等準脆性材料，斷裂力學模型能夠給出可以接受的結果。

但由于混凝土材料的微裂縫在受荷之前即存在，而且其大小、方向、出現的位置及裂縫分布具有隨機性；只有當裂縫尖端前的材料中存在均勻應力場時,斷裂力學理論才能應用于裂縫的演化分析，然而,在混凝土材料中上述情況幾乎不可能存在；在有限元分析過程中，每一荷載增量步甚至迭代步中的裂縫擴展都需要改變網格拓撲并重新劃分網格，這些因素大大限制了斷裂力學理論在結構分析中的應用。

1.5 損傷力學本構模型

工程結構或構件在荷載（如靜載或動載）和環(huán)境（如溫度、氧化、腐蝕等）作用下力學性能漸進劣化，這個過程即為損傷積累的過程。在微觀上體現為內部微缺陷、微裂紋的形成及進一步發(fā)展，從而導致材料中宏觀裂縫的出現，并使結構構件最終失效。以連續(xù)介質力學與不可逆熱力學為基礎的連續(xù)介質損傷力學把連續(xù)介質的微缺陷理解為連續(xù)的“損傷場”變量，并假定損傷的能量耗散過程滿足不可逆熱力學定律，利用連續(xù)介質力學的“唯象學”方法研究微缺陷（損傷）的發(fā)展及其對材料力學性質的影響。損傷理論的研究重點是：定義合理的損傷變量；建立材料損傷本構方程；探討損傷的演化規(guī)律；尋求測量損傷程度的方法；預估結構或構件的剩余壽命。

損傷理論的研究始于1958年Kachanov提出“連續(xù)性因子”的概念來描述金屬的蠕變斷裂。由于該模型簡單直觀、物理意義明確，此后的眾多損傷模型都在不同程度上借鑒了他的損傷理論思想。1963年Rabotnov又引入了“損傷因子”的概念研究金屬的蠕變本構方程，建立了損傷理論的雛形。在受損材料中，從細觀上對缺陷形式和損傷機制進行分析以確定有效面積是很困難的，為間接測定損傷，1971年Lemaitre提出了應變等價原理，并引入了有效應力的概念，成為將損傷變量引入材料應力－應變本構方程的橋梁。1977年Janson和Hult首次提出了“連續(xù)介質損傷力學”的概念，從此損傷力學在各國學者的努力下迅速發(fā)展，其中Lemaitre、Chaboche、Janson、Hult、Leckie-Hayhurst、Krajicinovic、Sidoroff、村上澄男等學者的研究工作為損傷理論的形成和發(fā)展作出了重要的貢獻。與此平行，Rice-Tracey、Gurson等學者從材料細觀結構出發(fā)，研究材料細觀結構變化的物理與力學過程，發(fā)展了材料細觀損傷力學。

在混凝土的損傷研究和實踐中，大量學者針對具體工程情況提出了各種不同的損傷本構模型，但是由于適用條件的特殊性及所建立模型的復雜化，很少有一種能夠有明確的物理意義、簡單的表達、便于工程師接受的一般損傷本構關系式。基于對損傷本構模型的思考,作者試圖以已有研究為基礎，致力于建立能夠反映混凝土破壞機理的一般損傷本構模型。

上述各種混凝土材料本構模型及其相互之間的交叉關系如下圖所示。

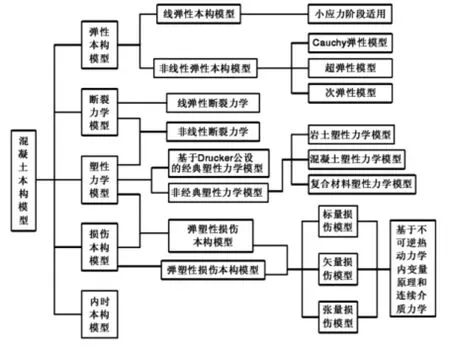
圖1 混凝土材料本構模型交叉關系圖

2 有關混凝土本構關系的展望

在混凝土的非線性有線元分析中，需要精度足夠而又計算方便的本構關系表達式，這一直是眾多研究者們重視的課題之一，這方面雖然已經有了很大的進展,但需要研究的問題仍然還有很多。可以預見今后對混凝土本構關系的研究,會在多層次、多角度進行。從實用分析的角度看,非線彈性模型、彈塑性模型已日趨成熟,并易于同通用的有限元程序匹配,因而還會更廣泛的推廣和應用,并有希望編入有關結構設計的規(guī)范中去,但在確定參數、改善精度方面還有相當的研究工作要做。為了適應混凝土的復雜加載和破壞的特點，將多種模式組合，如塑性斷裂、粘彈塑性、塑性損傷、內時塑性、內時損傷等這些交叉理論將會得到進一步研究。此外,有關動力分析的本構關系，基于隨機因素的本構關系值得進一步的探討。從試驗研究來看,在三向應力狀態(tài)下的應力應變測得的數據還不夠多。試驗方法也有待改進,特別是在不改變受力與變形條件的現代非機械、非破損的測量方法還期待有所突破。從破壞機理來看,斷裂力學、損傷力學的應用研究有很好的前景。這些理論結合微觀的觀察與分析來進行的研究，會在未來的十年中得到很大的發(fā)展。